华师大版七下(2024版)第七章 一元一次不等式 小结与评价 课件
文档属性
| 名称 | 华师大版七下(2024版)第七章 一元一次不等式 小结与评价 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-14 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
第七章 一元一次不等式
单元复习:小结与评价
01
教学目标
03
思考回顾
02
思维导图
04
典例精析
05
课堂练习
06
作业布置
01
教学目标
1.复习巩固不等式的概念及不等式的基本性质。
2.复习巩固一元一次不等式及其不等式组的解法,能够准确求解并正确表示解集。
3.能够正确分析实际问题中的不等关系,建立相应的不等式模型,能够准确列出不等式并求解。
4.通过复习、练习、讨论等方式,培养学生分析问题、解决问题的能力,以及逻辑推理和数学建模的能力。
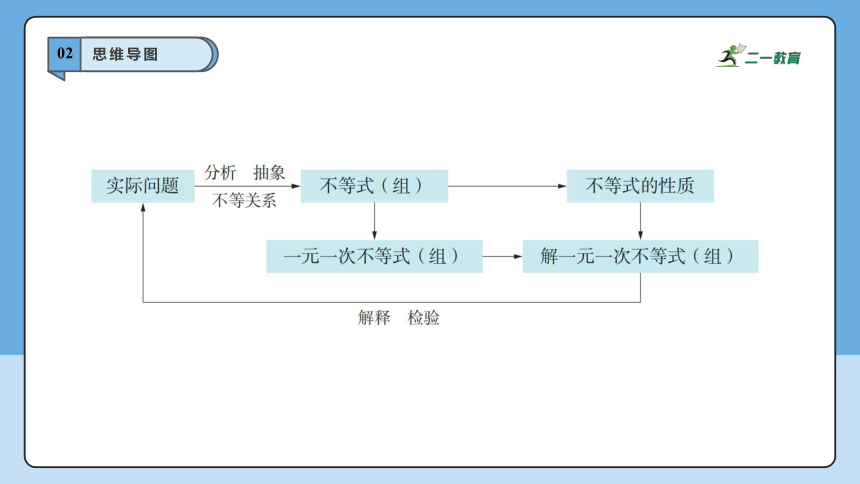
02
思维导图
1.什么是不等式?什么是不等式的解(集)?
用不等号连接的式子,常见的不等号有“>”、“<”、“≥”、“≤”、“≠”五种.
不等式的解:使不等式成立的未知数的值.
不等式的解集:一个含有未知数的不等式的所有解的集合,组成了这个不等式的解集.
03
思考回顾
2.不等式的性质有哪些?
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
03
思考回顾
一元一次不等式: ①不等式的左右两边都是整式,②只含有一个未知数,并且③未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
解一元一次不等式的步骤:去分母--去括号---移项---合并同类项--化系数为1
不等式解集的表示:大于向右,小于向左,有等实心,无等空心.
3.什么是一元一次不等式?怎么解一元一次不等式?如何在数轴上表示解集?
4. 如何用一元一次不等式解决有关的实际问题?
分析实际问题;找出正确的不等关系;设未知数列出一元一次不等式;解不等式;检验解的合理性。
03
思考回顾
一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
一元一次不等式组的解集:一般地,一元一次不等式组中各个不等式解集的公共部分,叫这个一元一次不等式组的解集。
一元一次不等式组的解法:
(1)解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分.
(3)根据公共部分写出不等式组解集.
5.什么是一元一次不等式组?如何解一元一次不等式组?如何确定其解集?
03
知识回顾
03
知识回顾
一元一次不等式组解集的表示方法及记忆规律:
不等式组(ax>b 同大取大
xa无解 大大小小找不到
1.不等式的知识源于实际问题.要学会分析现实世界中量与量之间的不等(大小)关系,并列出不等式
2.要注意把解一元一次不等式的过程与解一元一次方程的过程进行类比,把不等式的变形与方程的变形相对照,特别要注意不等式的基本性质3:不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.这种类比的思想,在以后的学习中还会经常用到.
3.将一元一次不等式的解集在数轴上表示出来,可以加深对一元一次不等式和一元一次不等式组的解集的理解,也便于直观地得到一元一次不等式组的解集.
4.不等式的基本性质,不仅用于解不等式,还可用来进行有关不等式的准理证明,在今后的数学学习中很有用.
03
思考回顾
例1:用不等式表示下列关系:
(1)a的2倍比8小;
(2)y的3倍与1的和大于3;
(3)x除以2的商加上2至多为5;
(4)a与b两数和的平方不大于2.
04
典例精析
04
典例精析
例2:对于不等式,则下列说法正确的有( ).
①5是不等式3x-5<2x的一个解;②0是不等式3x-5<2x的一个解;
③x<4也是不等式3x-5<2x的解集;④所有小于4的数都是不等式3x-5<2x的解。
A.1个 B.2个 C.3个 D.4个
C
例3:(1).由,得到的条件是( )
A.; B.; C.; D..
(2).下列变形中正确的是( )
A.由,得; B.由,得;
C.由,得;
D.由,得.
04
典例精析
D
C
例4:解不等式,并将其解集表示在数轴上.
解:去分母得:
移项得:
合并同类项得:
系数化为1得:
将解集表示在数轴上如下图所示
04
典例精析
例5:某高速公路工地需要实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到300m以外的安全区域.已知导火线的燃烧速度是0.6cm/s,人跑步的速度是5m/s.问:导火线必须超过多长,才能保证操作人员的安全?
[解析]设导火线长为。
由题意可列:
解得:
所以,导火线必须超过36cm,才能保证操作人员的安全。
04
典例精析
解:解不等式①得:
解不等式②得:
将解集表示在数轴上如图所示
所以不等式组的解集为:.
例6:解不等式组并把解集表示在数轴上.
04
典例精析
例7:若关于的不等式组的解集为,则的取值范围是__________.
04
典例精析
解:解不等式①得:
解不等式②得:
因为不等式组的解集为
根据口诀"同小取小",
所以的取值范围为:
05
课堂练习
【知识技能类作业】必做题:
1.下列说法中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.若关于的不等式组有且只有三个整数解,则的最大值是( )
A.3 B.4 C.5 D.6
A
C
04
课堂练习
【知识技能类作业】必做题:
3.解不等式的过程如下:①去分母,得;②去括号,得;③移项,合并同类项,得;④系数化为1,得.其中错误的一步是( )
A.① B.② C.③ D.④
D
04
课堂练习
【知识技能类作业】选做题:
4.若不等式x>y和(a-3)x<(a-3)y成立,则a的取值范围是 .
5.若是关于的一元一次不等式,则的值为 。
6.若关于的不等式组无解,则的取值范围是 .
a<3
m=-2
a≥-2
04
课堂练习
【综合拓展类作业】
7.已知,;,;都是关于x,y的二元一次方程的解.
(1)求a,b的值;
(2)当x为何值时,y的值小于0.
解:(1),;,;都是关于x,y的二元一次方程的解,
故将,;,代入二元一次方程得: ,
解得: .
04
课堂练习
【综合拓展类作业】
7.已知,;,;都是关于x,y的二元一次方程的解.
(1)求a,b的值;
(2)当x为何值时,y的值小于0.
解:(2)解:由(1)可知,
所以,
若要是y的值小于0,即 ,
解得:,
当时,y的值小于0.
06
课堂小结
06
作业布置
【知识技能类作业】必做题:
B
D
C
1.李老师在黑板上写了下面的式子,你认为哪一个不是不等式?( )
A.x<0 B.x=2 C.-2x+3≥1 D.-2a≤0
2.某电梯标明“最大载质量:1 000 kg”,若电梯载质量为x kg,x为非负数,则“最大载质量:1 000 kg”用不等式表示为( )
A.x>1 000 B.x<1 000 C.x≥1 000 D.x≤1 000
3.不等式5x≤-10的解集在数轴上表示为( )
06
作业布置
【知识技能类作业】选做题:
4.下列说法中,错误的是( )
A.不等式x<2的正整数解只有一个 B.-2是不等式2x-1<0的一个解
C.不等式-3x>9的解集是x>-3 D.不等式x<10的整数解有无数个
5.若x>y,则-3x+2 -3y+2(填“<”或“>”).
6.已知关于x的不等式(a-1)x>4的解集是,则a的取值范围是 .
C
<
a<1
06
作业布置
【综合拓展类作业】
7. 2022年2月4日至20日冬季奥运会在北京举行.某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售.已知“冰墩墩”摆件的进价为80元/个,“冰墩墩”挂件的进价为50元/个.
(1)若购进“冰墩墩”摆件和挂件共花费了11 400元,请分别求出购进“冰墩墩”摆件和挂件的数量;
解:(1)设购进“冰墩墩”摆件x个,“冰墩墩”挂件y个.
根据题意,得解得
答:购进“冰墩墩”摆件80个,“冰墩墩”挂件100个.
06
作业布置
【综合拓展类作业】
7. 2022年2月4日至20日冬季奥运会在北京举行.某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售.已知“冰墩墩”摆件的进价为80元/个,“冰墩墩”挂件的进价为50元/个.
(2)该商店计划将“冰墩墩”摆件售价定为100元/个,“冰墩墩”挂件售价定为60元/个,若购进的180个“冰墩墩”摆件和挂件全部售完,且至少盈利2 900元,求购进的“冰墩墩”挂件不能超过多少个.
解: (2)设购进“冰墩墩”挂件m个,则购进“冰墩墩”摆件(180-m)个.
根据题意,得(60-50)m+(100-80)(180-m)≥2 900,
解得m≤70.
答:购进的“冰墩墩”挂件不能超过70个.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第七章 一元一次不等式
单元复习:小结与评价
01
教学目标
03
思考回顾
02
思维导图
04
典例精析
05
课堂练习
06
作业布置
01
教学目标
1.复习巩固不等式的概念及不等式的基本性质。
2.复习巩固一元一次不等式及其不等式组的解法,能够准确求解并正确表示解集。
3.能够正确分析实际问题中的不等关系,建立相应的不等式模型,能够准确列出不等式并求解。
4.通过复习、练习、讨论等方式,培养学生分析问题、解决问题的能力,以及逻辑推理和数学建模的能力。
02
思维导图
1.什么是不等式?什么是不等式的解(集)?
用不等号连接的式子,常见的不等号有“>”、“<”、“≥”、“≤”、“≠”五种.
不等式的解:使不等式成立的未知数的值.
不等式的解集:一个含有未知数的不等式的所有解的集合,组成了这个不等式的解集.
03
思考回顾
2.不等式的性质有哪些?
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
03
思考回顾
一元一次不等式: ①不等式的左右两边都是整式,②只含有一个未知数,并且③未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
解一元一次不等式的步骤:去分母--去括号---移项---合并同类项--化系数为1
不等式解集的表示:大于向右,小于向左,有等实心,无等空心.
3.什么是一元一次不等式?怎么解一元一次不等式?如何在数轴上表示解集?
4. 如何用一元一次不等式解决有关的实际问题?
分析实际问题;找出正确的不等关系;设未知数列出一元一次不等式;解不等式;检验解的合理性。
03
思考回顾
一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
一元一次不等式组的解集:一般地,一元一次不等式组中各个不等式解集的公共部分,叫这个一元一次不等式组的解集。
一元一次不等式组的解法:
(1)解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分.
(3)根据公共部分写出不等式组解集.
5.什么是一元一次不等式组?如何解一元一次不等式组?如何确定其解集?
03
知识回顾
03
知识回顾
一元一次不等式组解集的表示方法及记忆规律:
不等式组(a
xa
1.不等式的知识源于实际问题.要学会分析现实世界中量与量之间的不等(大小)关系,并列出不等式
2.要注意把解一元一次不等式的过程与解一元一次方程的过程进行类比,把不等式的变形与方程的变形相对照,特别要注意不等式的基本性质3:不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.这种类比的思想,在以后的学习中还会经常用到.
3.将一元一次不等式的解集在数轴上表示出来,可以加深对一元一次不等式和一元一次不等式组的解集的理解,也便于直观地得到一元一次不等式组的解集.
4.不等式的基本性质,不仅用于解不等式,还可用来进行有关不等式的准理证明,在今后的数学学习中很有用.
03
思考回顾
例1:用不等式表示下列关系:
(1)a的2倍比8小;
(2)y的3倍与1的和大于3;
(3)x除以2的商加上2至多为5;
(4)a与b两数和的平方不大于2.
04
典例精析
04
典例精析
例2:对于不等式,则下列说法正确的有( ).
①5是不等式3x-5<2x的一个解;②0是不等式3x-5<2x的一个解;
③x<4也是不等式3x-5<2x的解集;④所有小于4的数都是不等式3x-5<2x的解。
A.1个 B.2个 C.3个 D.4个
C
例3:(1).由,得到的条件是( )
A.; B.; C.; D..
(2).下列变形中正确的是( )
A.由,得; B.由,得;
C.由,得;
D.由,得.
04
典例精析
D
C
例4:解不等式,并将其解集表示在数轴上.
解:去分母得:
移项得:
合并同类项得:
系数化为1得:
将解集表示在数轴上如下图所示
04
典例精析
例5:某高速公路工地需要实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到300m以外的安全区域.已知导火线的燃烧速度是0.6cm/s,人跑步的速度是5m/s.问:导火线必须超过多长,才能保证操作人员的安全?
[解析]设导火线长为。
由题意可列:
解得:
所以,导火线必须超过36cm,才能保证操作人员的安全。
04
典例精析
解:解不等式①得:
解不等式②得:
将解集表示在数轴上如图所示
所以不等式组的解集为:.
例6:解不等式组并把解集表示在数轴上.
04
典例精析
例7:若关于的不等式组的解集为,则的取值范围是__________.
04
典例精析
解:解不等式①得:
解不等式②得:
因为不等式组的解集为
根据口诀"同小取小",
所以的取值范围为:
05
课堂练习
【知识技能类作业】必做题:
1.下列说法中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.若关于的不等式组有且只有三个整数解,则的最大值是( )
A.3 B.4 C.5 D.6
A
C
04
课堂练习
【知识技能类作业】必做题:
3.解不等式的过程如下:①去分母,得;②去括号,得;③移项,合并同类项,得;④系数化为1,得.其中错误的一步是( )
A.① B.② C.③ D.④
D
04
课堂练习
【知识技能类作业】选做题:
4.若不等式x>y和(a-3)x<(a-3)y成立,则a的取值范围是 .
5.若是关于的一元一次不等式,则的值为 。
6.若关于的不等式组无解,则的取值范围是 .
a<3
m=-2
a≥-2
04
课堂练习
【综合拓展类作业】
7.已知,;,;都是关于x,y的二元一次方程的解.
(1)求a,b的值;
(2)当x为何值时,y的值小于0.
解:(1),;,;都是关于x,y的二元一次方程的解,
故将,;,代入二元一次方程得: ,
解得: .
04
课堂练习
【综合拓展类作业】
7.已知,;,;都是关于x,y的二元一次方程的解.
(1)求a,b的值;
(2)当x为何值时,y的值小于0.
解:(2)解:由(1)可知,
所以,
若要是y的值小于0,即 ,
解得:,
当时,y的值小于0.
06
课堂小结
06
作业布置
【知识技能类作业】必做题:
B
D
C
1.李老师在黑板上写了下面的式子,你认为哪一个不是不等式?( )
A.x<0 B.x=2 C.-2x+3≥1 D.-2a≤0
2.某电梯标明“最大载质量:1 000 kg”,若电梯载质量为x kg,x为非负数,则“最大载质量:1 000 kg”用不等式表示为( )
A.x>1 000 B.x<1 000 C.x≥1 000 D.x≤1 000
3.不等式5x≤-10的解集在数轴上表示为( )
06
作业布置
【知识技能类作业】选做题:
4.下列说法中,错误的是( )
A.不等式x<2的正整数解只有一个 B.-2是不等式2x-1<0的一个解
C.不等式-3x>9的解集是x>-3 D.不等式x<10的整数解有无数个
5.若x>y,则-3x+2 -3y+2(填“<”或“>”).
6.已知关于x的不等式(a-1)x>4的解集是,则a的取值范围是 .
C
<
a<1
06
作业布置
【综合拓展类作业】
7. 2022年2月4日至20日冬季奥运会在北京举行.某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售.已知“冰墩墩”摆件的进价为80元/个,“冰墩墩”挂件的进价为50元/个.
(1)若购进“冰墩墩”摆件和挂件共花费了11 400元,请分别求出购进“冰墩墩”摆件和挂件的数量;
解:(1)设购进“冰墩墩”摆件x个,“冰墩墩”挂件y个.
根据题意,得解得
答:购进“冰墩墩”摆件80个,“冰墩墩”挂件100个.
06
作业布置
【综合拓展类作业】
7. 2022年2月4日至20日冬季奥运会在北京举行.某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售.已知“冰墩墩”摆件的进价为80元/个,“冰墩墩”挂件的进价为50元/个.
(2)该商店计划将“冰墩墩”摆件售价定为100元/个,“冰墩墩”挂件售价定为60元/个,若购进的180个“冰墩墩”摆件和挂件全部售完,且至少盈利2 900元,求购进的“冰墩墩”挂件不能超过多少个.
解: (2)设购进“冰墩墩”挂件m个,则购进“冰墩墩”摆件(180-m)个.
根据题意,得(60-50)m+(100-80)(180-m)≥2 900,
解得m≤70.
答:购进的“冰墩墩”挂件不能超过70个.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
