第26-29章巩固卷-2024-2025学年数学九年级下册人教版(含解析)
文档属性
| 名称 | 第26-29章巩固卷-2024-2025学年数学九年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 14:17:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第26-29章巩固卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一个三棱柱无论怎么摆放,其主视图不可能是( )
A. B. C. D.
2.如图所示,在矩形网格中,每个小正方形的边长为1,的三个顶点都在格点上,则的值为( )
A. B. C. D.
3.下列所给的两个相关联的量,它们是反比例关系的是( )
A.面积一定时,三角形的底a与高h之间的关系
B.周长一定时,长方形的长x与宽y之间的关系
C.工作时间一定时,工作总量w与工作效率v之间的关系
D.汽车的速度一定时,它的行驶路程S与行驶时间t之间的关系
4.我们中国的国旗是长方形的,这个长方形被誉为最美长方形,宽与长的比符合黄金比,则它们的比值是( )
A. B.0.618 C.6.18 D.
5.第14届国际数学教育大会会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形和一个小正方形拼成的大正方形.若,则( )
A. B. C. D.
6.如图,将一个含角的三角尺放在直角坐标系中,使直角顶点与原点重合,顶点分别在反比例函数和上的图象上,则的值为( )
A. B.12 C. D.
7.如图,在中,是斜边的中点,以点为圆心的半圆与相切于点,交于点,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,四边形与四边形位似,位似中心是O,若,且四边形的周长为4,则四边形的周长为( )
A.6 B.9 C.12 D.27
二、填空题
9.计算: .
10.如图,在中,,,则的长是 .
11.定义:若线段上有一点满足或,则称点为线段的黄金分割点.在如图所示的五角星图案中,已知点是线段的黄金分割点,若,则线段的长为 .
12.若点都在反比例函数图象上,则的值为 .
13.如图,在矩形纸片中,,,截去矩形.若剩下的矩形与矩形相似,则的长为 .
14.如图,在平行四边形中,对角线,点E为上一点,且,连接、,交于点F,若,,则边的长为 .
15.在函数(为常数)的图象上有三点,,,则函数值,,的大小关系为 .
16.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
三、解答题
17.计算:.
18.如图,一个几何体模具由大小相同的小正方体搭成:
(1)请画出这个几何体模具的三视图;
(2)若工人师傅手里还有一些相同的正方体,要保持俯视图和左视图不变,最多可以再添加______个小立方体.
19.如图,在中,,.
(1)求的度数;
(2)分别以,为圆心,大于的长为半径画弧,两弧交于点,,作直线,交于点,连接,则的度数为______,并说明理由.
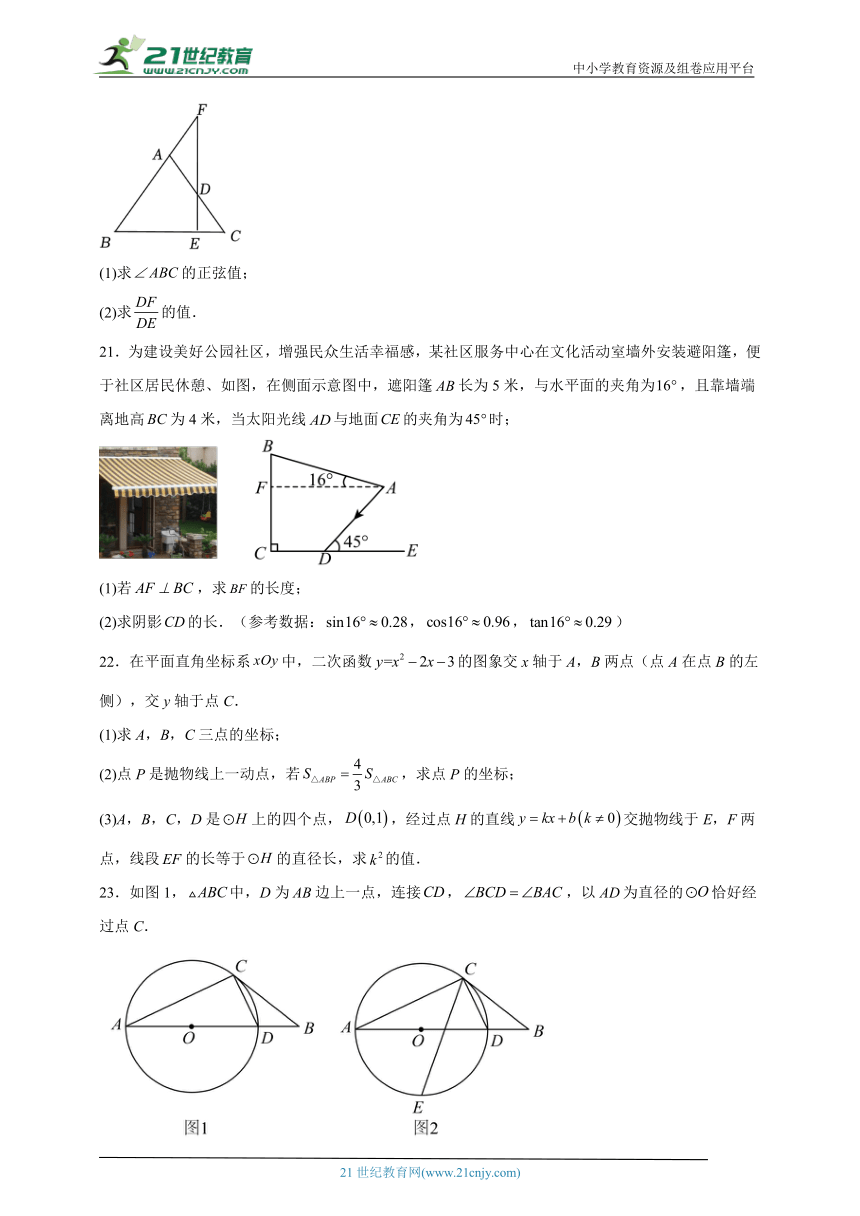
20.如图,已知中,,,D是的中点,于点E,的延长线交于点F.
(1)求的正弦值;
(2)求的值.
21.为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装避阳篷,便于社区居民休憩、如图,在侧面示意图中,遮阳篷长为5米,与水平面的夹角为,且靠墙端离地高为4米,当太阳光线与地面的夹角为时;
(1)若,求的长度;
(2)求阴影的长.(参考数据:,,)
22.在平面直角坐标系中,二次函数的图象交x轴于A,B两点(点A在点B的左侧),交y轴于点C.
(1)求A,B,C三点的坐标;
(2)点P是抛物线上一动点,若,求点P的坐标;
(3)A,B,C,D是上的四个点,,经过点H的直线交抛物线于E,F两点,线段的长等于的直径长,求的值.
23.如图1,中,D为边上一点,连接,,以为直径的恰好经过点C.
(1)求证:是的切线;
(2)若,.
①求 的半径r;
②如图 2,若点E是的中点(点E,C在直径的异侧),连接,求 的长.
24.如图,已知二次函数(a是常数,且)的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,并将图像中位于y轴左侧的部分作关于y轴的对称图像,该对称图像记为图像.
(1)则点A坐标为 ,点B坐标为 ;
(2)若直线是常数交图像于点D,E(点D在点E的左侧),并与图像 交于点F,若 ,求a与m的数量关系;
(3)当时,连接,图像上是否存在一点P,过点P作⊥直线,垂足为点Q,连接,使得?若存在,求点P坐标;若不存在,请说明理由.
《第26-29章巩固卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A B A B C B C C
1.A
【分析】本题考查了立体图形的三视图,掌握立体图形的特点,三视图的特点是解题的关键.
根据立体图形的特点进行分析即可求解.
【详解】解:三棱柱中侧面是长方形,上下底面是三角形,
∴主视图中可能出现长方形(正方形)和三角形,不可能出现圆形,
故选:A .
2.B
【分析】本题考查了正切的定义,作交于,由题意可得,,,再由正切的定义计算即可得解.
【详解】解:如图,作交于,
,
由题意可得:,,,
∴,
故选:B.
3.A
【分析】本题考查了反比例函数的应用,掌握两个相关联的量对应的两个数值的乘积一定时是反比例关系是解决问题的关键.根据两个相关联的量对应的两个数值的比值一定时是正比例,乘积一定时是反比例判断即可.
【详解】A.∵三角形的面积(定值),
∴三角形的底a与高h之间是反比例关系,故该选项符合题意;
B.∵矩形的周长(定值),
∴长方形的长x与宽y不是反比例关系,故该选项不符合题意;
C.∵工作时间(定值),
∴工作总量w与工作效率v之间是正比例关系,故该选项不符合题意;
D.∵汽车的速度(定值),
∴汽车行驶路程S与行驶时间t之间是正比例关系,故该选项不符合题意;
故选:A.
4.B
【分析】本题考查了黄金分割,根据黄金比进行作答即可.
【详解】解:依题意,这个长方形被誉为最美长方形,宽与长的比符合黄金比,
则它们的比值是0.618,
故选:B
5.C
【分析】本题考查了正方形的性质、全等三角形的性质、勾股定理、正弦的定义,设,则,由全等三角形的性质结合正方形的性质可得,,从而可得,由勾股定理可得,再由正弦的定义计算即可得解.
【详解】解:∵,
∴设,则,
∵,四边形为正方形,
∴,,
∴,即,
∴,
∵,
∴,
∴,
故选:C.
6.B
【分析】过A作轴于E,过B作轴于F,通过,得到,设,于是得到,,从而得到,于是求得结果.此题考查相似三角形的判定与性质,反比例函数图象上点的坐标特征,解题关键在于作辅助线和利用三角函数进行解答.
【详解】解:过A作轴于E,过B作轴于F,
,,
,
,
,
,
,
设,
,,
,,
,
.
故选:B.
7.C
【分析】连接,过点D作于点G,利用分割法,计算面积即可.
本题考查了直角三角形的性质,三角函数的应用,扇形的面积公式,分割法计算面积,熟练掌握直角三角形的性质,扇形面积公式是解题的关键.
【详解】解:连接,过点D作于点G,
∵,,是斜边的中点,以点为圆心的半圆与相切于点,
∴,,,
∴,,,
∴,
∴,,
∴阴影部分的面积为:
,
故选:C.
8.C
【分析】本题考查了位似图形的性质,根据相似比等于位似比可得:四边形的周长四边形的周长,据此解答即可求解,掌握位似图形的性质是解题的关键.
【详解】解:∵,
∴,
∵四边形与四边形位似,位似中心是,
∴四边形与四边形的相似比为,
∴四边形的周长四边形的周长,
∵四边形的周长为,
∴四边形的周长为,
故选:C.
9./
【分析】此题考查了实数的混合运算,利用特殊角的三角函数值、绝对值、负整数指数幂计算即可.
【详解】解:
故答案为:
10.12
【分析】本题考查了等腰三角形的性质,正弦,勾股定理等知识.作于,由,可得,由,可求,由勾股定理得,,进而可求的长.
【详解】解:如图,作于,
∵,
∴,
∴,即,
解得,,
由勾股定理得,,
∴,
故答案为:12.
11./
【分析】本题考查的是黄金分割的概念,熟记线段的黄金分割点有两个是解题的关键.根据黄金分割的定义可得,继而由求出,再由线段和差计算即可求解.
【详解】解:由题意得,,
∴,
∴,
故答案为:.
12.
【分析】本题考查了反比例函数解析式的确定,熟练掌握反比例函数的性质是解题的关键.根据解析式与点的坐标关系,代入计算即可.
【详解】解:∵点都在反比例函数的图象上,
∴,即,
∴,
∴,
∴
故答案为:.
13.
【分析】本题考查了相似多边形的性质,熟练掌握相似多边形的性质是解答本题的关键.
由相似多边形的对应边成比例可得,代入数据计算即可.
【详解】解:为矩形,
,
矩形与矩形相似,
,即,
解得:,
故答案为:.
14.5
【分析】作的平分线交于,过作交于,由平行四边形和得到,,,,再由,的平分线交于,得到,设,,则,由,得到,求出,,再根据,求出,然后根据得到,再根据,,得到,代入解方程求出,,最后根据求解即可.
【详解】解:作的平分线交于,过作交于,
∵平行四边形中,对角线, ,
∴,,,,
∴,
∵,的平分线交于,
∴,
设,,
∴,
∵,
∴,
∴,
∴,,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
整理得,
∵,,
∴,整理得,
∴,
平方后整理得,
解得或(此时,故舍去),
∴(负值舍去),
∴,
∴,
故答案为:.
【点睛】本题考查相似三角形的判定与性质,解直角三角形有关的计算,平行四边形的性质,解特殊的一元二次方程等知识点.
15.
【分析】本题考查反比例函数的图象与性质,解题的关键是掌握反比例函数的图象与性质,根据题意得:,可得反比例函数的图象经过第二,四象限,在每一象限内随的增大而增大,进行解答即可.
【详解】解:,
反比例函数的图象经过第二,四象限,在每一象限内随的增大而增大,
点,在第二象限,
,
,
点在第四象限,
,
,
.
故答案为:.
16.
【分析】本题主要考查了反比例函数的实际应用,待定系数法求反比例函数解析式,反比例函数的性质,熟练掌握以上知识点是解题的关键.先求得反比例函数关系式,求得时,,再利用反比例函数的增减性质,可求得答案.
【详解】解:设,代入
随的增大而减小
当时,
其限制电流不能超过,那么用电器可变电阻应控制的范围是
故答案为:.
17.
【分析】本题主要考查了含特殊角的三角函数值运算、二次根式运算、化简绝对值等知识,熟练掌握相关运算法则和性质是解题关键.首先根据化简绝对值、代入特殊角的三角形函数值,再计算二次根式的乘法,然后计算加减求解即可.
【详解】解:原式
.
18.(1)见解析
(2)5
【分析】本题考查几何体的三视图画法.
(1)根据三视图的画法,画出图形即可求解;
(2)从俯视图的角度出发,同时考虑左视图的情况,即可求解.
【详解】(1)解:三视图如图:
;
(2)解:由俯视图和左视图不变,在俯视图上可增加
,
最多可以再添加5个小立方体.
故答案为:5.
19.(1)
(2),理由见解析
【分析】本题考查了勾股定理逆定理、解直角三角形、线段垂直平分线的性质、直角三角形的性质等知识点,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由题意可得,再由勾股定理逆定理得出为直角三角形,且,即可得解;
(2)解直角三角形可得,由作图可得垂直平分,可得,由直角三角形的性质可得,从而得出,再由三角形外角的定义及性质计算即可得解.
【详解】(1)解:∵,
∴,
∴,
∴为直角三角形,且;
(2)解:,理由如下:
∵,,
∴,
∴,
由作图可得垂直平分,
∴,
∴,
∴,
∴.
20.(1)
(2)2
【分析】(1)过点作于点,由得到是等腰三角形,由三线合一得到,由勾股定理求得,根据正弦的定义即可得到答案;
(2)由,得到,由是的中点,得到是的中位线,求得,由得到,求得,得到,即可得到答案.
【详解】(1)解:过点作于点,
,
是等腰三角形,
又,
.
在中,,
.
(2)解:,,
,
∴,
又是的中点,
∴,
∴,
是的中位线,
,.
.
,,
.
,即,
解得.
.
.
【点睛】此题考查了平行线分线段成比例定理,相似三角形的性质与判定,三角形的中位线,等腰三角形的三线合一,三角函数的定义,勾股定理等知识,熟练掌握相关定理是解题的关键.
21.(1)1.4米
(2)2.2米
【分析】本题考查了解直角三角形的应用,矩形的性质和判定,等腰三角形的判定.
(1)根据正弦的定义求解即可;
(2)过A作于K,根据余弦的定义求出,再证明是矩形,可得,,再证明是等腰三角形,可得,进而可求.
【详解】(1)解:由题意知:,,
∴,
在中,米;
(2)解:过A作于K,则,
米,
∴米,
∵四边形是矩形,
∴米,米,
由题意知:,
∴,
∴米,
∴米,
∴阴影的长为2.2米.
22.(1)点A、B、C的坐标分别为:、、;
(2)点P的坐标为或或;
(3)
【分析】本题考查的是二次函数综合运用,涉及到圆的基本知识,解直角三角形,面积的计算等,数据处理是本题的难点.
(1)对于,当时,,令,则或3,即可求解;
(2)若,则,据此即可求解;
(3)求出点,由,得到,即可求解.
【详解】(1)解:对于,当时,,
令,则或3,
即点A、B、C的坐标分别为:、、;
(2)解:若,则,
即,
解得:或1,
即点P的坐标为或或;
(3)解:的中垂线为,的中垂线为,即点,
由点B、H的坐标得,圆H的半径为,则直径为,
设直线的表达式为:,
联立和抛物线的表达式得:,
则,,
则,
作轴交过点F和y轴的平行线于点T,
由E、F的坐标知,,则,
则,
即,
解得:(负值已舍去).
23.(1)见详解
(2)①,②
【分析】(1)连接,根据题意得,结合圆和等腰三角形的性质得,则,结合已知得,即可证明;
(2)①根据题意知和,则,解得和,求得,即可得半径;
②连接,,则,进一步得到和,以及,过点A作于点H,过点D作于点G,则,是等腰直角三角形,求得和,结合等面积法即可.
【详解】(1)证明:连接,如图,
∵为的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
则是的切线;
(2)解:①∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
则,
∴,
故 的半径;
②连接,,如图,
∵点E是的中点,
∴,
∴,
∵为的直径,
∴,
∴,
∵,
∴,
∵,
由勾股定理得:,
∴,
过点A作于点H,过点D作于点G,则,是等腰直角三角形,
∴,,
∴,
即,
∴.
【点睛】本题主要考查圆的性质,涉及直径所对的圆周角为直角,等腰三角形的性质,切线的判定,解直角三角形,同弧所对圆周角相等,相似三角形的判定和性质,解题的关键是熟悉圆的性质和相似三角形的判定和性质.
24.(1)
(2)
(3)
【分析】(1)令,求出x值即可解题;
(2)由二次函数知,其对称轴为直线故设点则点则点的横坐标为: 则求出值解题即可;
(3)证明得到求出点 ,即可求解.
【详解】(1)解:令
解得或
即点、的坐标分别为:
故答案为: ;
(2)由题意得: ,
由二次函数)得,其对称轴为直线,
设点,则点则点的横坐标为
则
解得
∴;
(3)存在, 理由:
取则,
当时,时,,
∴点的坐标为,
由点、的坐标得,
设边上的高为,
则,即
解得
∵
∴
设直线的解析式为,代入得:
,解得,
∴直线的表达式为:
设点, 点
过点作轴的平行线交过点和轴的平行线于点,交过点和轴的平行线于点,
,,
,
,
即
解得:
即点
将点的坐标代入得
解得:(舍去)或 ,
则
即点.
【点睛】主要考查了二次函数的图像和性质,掌握待定系数法求函数解析式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第26-29章巩固卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一个三棱柱无论怎么摆放,其主视图不可能是( )
A. B. C. D.
2.如图所示,在矩形网格中,每个小正方形的边长为1,的三个顶点都在格点上,则的值为( )
A. B. C. D.
3.下列所给的两个相关联的量,它们是反比例关系的是( )
A.面积一定时,三角形的底a与高h之间的关系
B.周长一定时,长方形的长x与宽y之间的关系
C.工作时间一定时,工作总量w与工作效率v之间的关系
D.汽车的速度一定时,它的行驶路程S与行驶时间t之间的关系
4.我们中国的国旗是长方形的,这个长方形被誉为最美长方形,宽与长的比符合黄金比,则它们的比值是( )
A. B.0.618 C.6.18 D.
5.第14届国际数学教育大会会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形和一个小正方形拼成的大正方形.若,则( )
A. B. C. D.
6.如图,将一个含角的三角尺放在直角坐标系中,使直角顶点与原点重合,顶点分别在反比例函数和上的图象上,则的值为( )
A. B.12 C. D.
7.如图,在中,是斜边的中点,以点为圆心的半圆与相切于点,交于点,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,四边形与四边形位似,位似中心是O,若,且四边形的周长为4,则四边形的周长为( )
A.6 B.9 C.12 D.27
二、填空题
9.计算: .
10.如图,在中,,,则的长是 .
11.定义:若线段上有一点满足或,则称点为线段的黄金分割点.在如图所示的五角星图案中,已知点是线段的黄金分割点,若,则线段的长为 .
12.若点都在反比例函数图象上,则的值为 .
13.如图,在矩形纸片中,,,截去矩形.若剩下的矩形与矩形相似,则的长为 .
14.如图,在平行四边形中,对角线,点E为上一点,且,连接、,交于点F,若,,则边的长为 .
15.在函数(为常数)的图象上有三点,,,则函数值,,的大小关系为 .
16.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
三、解答题
17.计算:.
18.如图,一个几何体模具由大小相同的小正方体搭成:
(1)请画出这个几何体模具的三视图;
(2)若工人师傅手里还有一些相同的正方体,要保持俯视图和左视图不变,最多可以再添加______个小立方体.
19.如图,在中,,.
(1)求的度数;
(2)分别以,为圆心,大于的长为半径画弧,两弧交于点,,作直线,交于点,连接,则的度数为______,并说明理由.
20.如图,已知中,,,D是的中点,于点E,的延长线交于点F.
(1)求的正弦值;
(2)求的值.
21.为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装避阳篷,便于社区居民休憩、如图,在侧面示意图中,遮阳篷长为5米,与水平面的夹角为,且靠墙端离地高为4米,当太阳光线与地面的夹角为时;
(1)若,求的长度;
(2)求阴影的长.(参考数据:,,)
22.在平面直角坐标系中,二次函数的图象交x轴于A,B两点(点A在点B的左侧),交y轴于点C.
(1)求A,B,C三点的坐标;
(2)点P是抛物线上一动点,若,求点P的坐标;
(3)A,B,C,D是上的四个点,,经过点H的直线交抛物线于E,F两点,线段的长等于的直径长,求的值.
23.如图1,中,D为边上一点,连接,,以为直径的恰好经过点C.
(1)求证:是的切线;
(2)若,.
①求 的半径r;
②如图 2,若点E是的中点(点E,C在直径的异侧),连接,求 的长.
24.如图,已知二次函数(a是常数,且)的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,并将图像中位于y轴左侧的部分作关于y轴的对称图像,该对称图像记为图像.
(1)则点A坐标为 ,点B坐标为 ;
(2)若直线是常数交图像于点D,E(点D在点E的左侧),并与图像 交于点F,若 ,求a与m的数量关系;
(3)当时,连接,图像上是否存在一点P,过点P作⊥直线,垂足为点Q,连接,使得?若存在,求点P坐标;若不存在,请说明理由.
《第26-29章巩固卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A B A B C B C C
1.A
【分析】本题考查了立体图形的三视图,掌握立体图形的特点,三视图的特点是解题的关键.
根据立体图形的特点进行分析即可求解.
【详解】解:三棱柱中侧面是长方形,上下底面是三角形,
∴主视图中可能出现长方形(正方形)和三角形,不可能出现圆形,
故选:A .
2.B
【分析】本题考查了正切的定义,作交于,由题意可得,,,再由正切的定义计算即可得解.
【详解】解:如图,作交于,
,
由题意可得:,,,
∴,
故选:B.
3.A
【分析】本题考查了反比例函数的应用,掌握两个相关联的量对应的两个数值的乘积一定时是反比例关系是解决问题的关键.根据两个相关联的量对应的两个数值的比值一定时是正比例,乘积一定时是反比例判断即可.
【详解】A.∵三角形的面积(定值),
∴三角形的底a与高h之间是反比例关系,故该选项符合题意;
B.∵矩形的周长(定值),
∴长方形的长x与宽y不是反比例关系,故该选项不符合题意;
C.∵工作时间(定值),
∴工作总量w与工作效率v之间是正比例关系,故该选项不符合题意;
D.∵汽车的速度(定值),
∴汽车行驶路程S与行驶时间t之间是正比例关系,故该选项不符合题意;
故选:A.
4.B
【分析】本题考查了黄金分割,根据黄金比进行作答即可.
【详解】解:依题意,这个长方形被誉为最美长方形,宽与长的比符合黄金比,
则它们的比值是0.618,
故选:B
5.C
【分析】本题考查了正方形的性质、全等三角形的性质、勾股定理、正弦的定义,设,则,由全等三角形的性质结合正方形的性质可得,,从而可得,由勾股定理可得,再由正弦的定义计算即可得解.
【详解】解:∵,
∴设,则,
∵,四边形为正方形,
∴,,
∴,即,
∴,
∵,
∴,
∴,
故选:C.
6.B
【分析】过A作轴于E,过B作轴于F,通过,得到,设,于是得到,,从而得到,于是求得结果.此题考查相似三角形的判定与性质,反比例函数图象上点的坐标特征,解题关键在于作辅助线和利用三角函数进行解答.
【详解】解:过A作轴于E,过B作轴于F,
,,
,
,
,
,
,
设,
,,
,,
,
.
故选:B.
7.C
【分析】连接,过点D作于点G,利用分割法,计算面积即可.
本题考查了直角三角形的性质,三角函数的应用,扇形的面积公式,分割法计算面积,熟练掌握直角三角形的性质,扇形面积公式是解题的关键.
【详解】解:连接,过点D作于点G,
∵,,是斜边的中点,以点为圆心的半圆与相切于点,
∴,,,
∴,,,
∴,
∴,,
∴阴影部分的面积为:
,
故选:C.
8.C
【分析】本题考查了位似图形的性质,根据相似比等于位似比可得:四边形的周长四边形的周长,据此解答即可求解,掌握位似图形的性质是解题的关键.
【详解】解:∵,
∴,
∵四边形与四边形位似,位似中心是,
∴四边形与四边形的相似比为,
∴四边形的周长四边形的周长,
∵四边形的周长为,
∴四边形的周长为,
故选:C.
9./
【分析】此题考查了实数的混合运算,利用特殊角的三角函数值、绝对值、负整数指数幂计算即可.
【详解】解:
故答案为:
10.12
【分析】本题考查了等腰三角形的性质,正弦,勾股定理等知识.作于,由,可得,由,可求,由勾股定理得,,进而可求的长.
【详解】解:如图,作于,
∵,
∴,
∴,即,
解得,,
由勾股定理得,,
∴,
故答案为:12.
11./
【分析】本题考查的是黄金分割的概念,熟记线段的黄金分割点有两个是解题的关键.根据黄金分割的定义可得,继而由求出,再由线段和差计算即可求解.
【详解】解:由题意得,,
∴,
∴,
故答案为:.
12.
【分析】本题考查了反比例函数解析式的确定,熟练掌握反比例函数的性质是解题的关键.根据解析式与点的坐标关系,代入计算即可.
【详解】解:∵点都在反比例函数的图象上,
∴,即,
∴,
∴,
∴
故答案为:.
13.
【分析】本题考查了相似多边形的性质,熟练掌握相似多边形的性质是解答本题的关键.
由相似多边形的对应边成比例可得,代入数据计算即可.
【详解】解:为矩形,
,
矩形与矩形相似,
,即,
解得:,
故答案为:.
14.5
【分析】作的平分线交于,过作交于,由平行四边形和得到,,,,再由,的平分线交于,得到,设,,则,由,得到,求出,,再根据,求出,然后根据得到,再根据,,得到,代入解方程求出,,最后根据求解即可.
【详解】解:作的平分线交于,过作交于,
∵平行四边形中,对角线, ,
∴,,,,
∴,
∵,的平分线交于,
∴,
设,,
∴,
∵,
∴,
∴,
∴,,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
整理得,
∵,,
∴,整理得,
∴,
平方后整理得,
解得或(此时,故舍去),
∴(负值舍去),
∴,
∴,
故答案为:.
【点睛】本题考查相似三角形的判定与性质,解直角三角形有关的计算,平行四边形的性质,解特殊的一元二次方程等知识点.
15.
【分析】本题考查反比例函数的图象与性质,解题的关键是掌握反比例函数的图象与性质,根据题意得:,可得反比例函数的图象经过第二,四象限,在每一象限内随的增大而增大,进行解答即可.
【详解】解:,
反比例函数的图象经过第二,四象限,在每一象限内随的增大而增大,
点,在第二象限,
,
,
点在第四象限,
,
,
.
故答案为:.
16.
【分析】本题主要考查了反比例函数的实际应用,待定系数法求反比例函数解析式,反比例函数的性质,熟练掌握以上知识点是解题的关键.先求得反比例函数关系式,求得时,,再利用反比例函数的增减性质,可求得答案.
【详解】解:设,代入
随的增大而减小
当时,
其限制电流不能超过,那么用电器可变电阻应控制的范围是
故答案为:.
17.
【分析】本题主要考查了含特殊角的三角函数值运算、二次根式运算、化简绝对值等知识,熟练掌握相关运算法则和性质是解题关键.首先根据化简绝对值、代入特殊角的三角形函数值,再计算二次根式的乘法,然后计算加减求解即可.
【详解】解:原式
.
18.(1)见解析
(2)5
【分析】本题考查几何体的三视图画法.
(1)根据三视图的画法,画出图形即可求解;
(2)从俯视图的角度出发,同时考虑左视图的情况,即可求解.
【详解】(1)解:三视图如图:
;
(2)解:由俯视图和左视图不变,在俯视图上可增加
,
最多可以再添加5个小立方体.
故答案为:5.
19.(1)
(2),理由见解析
【分析】本题考查了勾股定理逆定理、解直角三角形、线段垂直平分线的性质、直角三角形的性质等知识点,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由题意可得,再由勾股定理逆定理得出为直角三角形,且,即可得解;
(2)解直角三角形可得,由作图可得垂直平分,可得,由直角三角形的性质可得,从而得出,再由三角形外角的定义及性质计算即可得解.
【详解】(1)解:∵,
∴,
∴,
∴为直角三角形,且;
(2)解:,理由如下:
∵,,
∴,
∴,
由作图可得垂直平分,
∴,
∴,
∴,
∴.
20.(1)
(2)2
【分析】(1)过点作于点,由得到是等腰三角形,由三线合一得到,由勾股定理求得,根据正弦的定义即可得到答案;
(2)由,得到,由是的中点,得到是的中位线,求得,由得到,求得,得到,即可得到答案.
【详解】(1)解:过点作于点,
,
是等腰三角形,
又,
.
在中,,
.
(2)解:,,
,
∴,
又是的中点,
∴,
∴,
是的中位线,
,.
.
,,
.
,即,
解得.
.
.
【点睛】此题考查了平行线分线段成比例定理,相似三角形的性质与判定,三角形的中位线,等腰三角形的三线合一,三角函数的定义,勾股定理等知识,熟练掌握相关定理是解题的关键.
21.(1)1.4米
(2)2.2米
【分析】本题考查了解直角三角形的应用,矩形的性质和判定,等腰三角形的判定.
(1)根据正弦的定义求解即可;
(2)过A作于K,根据余弦的定义求出,再证明是矩形,可得,,再证明是等腰三角形,可得,进而可求.
【详解】(1)解:由题意知:,,
∴,
在中,米;
(2)解:过A作于K,则,
米,
∴米,
∵四边形是矩形,
∴米,米,
由题意知:,
∴,
∴米,
∴米,
∴阴影的长为2.2米.
22.(1)点A、B、C的坐标分别为:、、;
(2)点P的坐标为或或;
(3)
【分析】本题考查的是二次函数综合运用,涉及到圆的基本知识,解直角三角形,面积的计算等,数据处理是本题的难点.
(1)对于,当时,,令,则或3,即可求解;
(2)若,则,据此即可求解;
(3)求出点,由,得到,即可求解.
【详解】(1)解:对于,当时,,
令,则或3,
即点A、B、C的坐标分别为:、、;
(2)解:若,则,
即,
解得:或1,
即点P的坐标为或或;
(3)解:的中垂线为,的中垂线为,即点,
由点B、H的坐标得,圆H的半径为,则直径为,
设直线的表达式为:,
联立和抛物线的表达式得:,
则,,
则,
作轴交过点F和y轴的平行线于点T,
由E、F的坐标知,,则,
则,
即,
解得:(负值已舍去).
23.(1)见详解
(2)①,②
【分析】(1)连接,根据题意得,结合圆和等腰三角形的性质得,则,结合已知得,即可证明;
(2)①根据题意知和,则,解得和,求得,即可得半径;
②连接,,则,进一步得到和,以及,过点A作于点H,过点D作于点G,则,是等腰直角三角形,求得和,结合等面积法即可.
【详解】(1)证明:连接,如图,
∵为的直径,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
则是的切线;
(2)解:①∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
则,
∴,
故 的半径;
②连接,,如图,
∵点E是的中点,
∴,
∴,
∵为的直径,
∴,
∴,
∵,
∴,
∵,
由勾股定理得:,
∴,
过点A作于点H,过点D作于点G,则,是等腰直角三角形,
∴,,
∴,
即,
∴.
【点睛】本题主要考查圆的性质,涉及直径所对的圆周角为直角,等腰三角形的性质,切线的判定,解直角三角形,同弧所对圆周角相等,相似三角形的判定和性质,解题的关键是熟悉圆的性质和相似三角形的判定和性质.
24.(1)
(2)
(3)
【分析】(1)令,求出x值即可解题;
(2)由二次函数知,其对称轴为直线故设点则点则点的横坐标为: 则求出值解题即可;
(3)证明得到求出点 ,即可求解.
【详解】(1)解:令
解得或
即点、的坐标分别为:
故答案为: ;
(2)由题意得: ,
由二次函数)得,其对称轴为直线,
设点,则点则点的横坐标为
则
解得
∴;
(3)存在, 理由:
取则,
当时,时,,
∴点的坐标为,
由点、的坐标得,
设边上的高为,
则,即
解得
∵
∴
设直线的解析式为,代入得:
,解得,
∴直线的表达式为:
设点, 点
过点作轴的平行线交过点和轴的平行线于点,交过点和轴的平行线于点,
,,
,
,
即
解得:
即点
将点的坐标代入得
解得:(舍去)或 ,
则
即点.
【点睛】主要考查了二次函数的图像和性质,掌握待定系数法求函数解析式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
