20.1.2中位数与众数(含解析) 人教版数学八年级下册
文档属性
| 名称 | 20.1.2中位数与众数(含解析) 人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 217.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 19:35:25 | ||
图片预览



文档简介
20.1.2中位数与众数
一、单选题
1.2024年,中国将迎来一系列重要的周年纪念活动,某校开展了主题为“牢记历史 吾辈自强”的演讲比赛,九年级8名同学参加该演讲比赛的成绩分别为76,78,80,85,80,74,78,80.则这组数据的众数和中位数分别为( )
A.80,79 B.80,78 C.78,79 D.80,80
2.金牛区某校八年级学生参加体质健康测试,有一组9个女生做一分钟的仰卧起坐个数如表中数据所示,则这组仰卧起坐个数的众数和中位数分别是( )
学生(序号) 1号 2号 3号 4号 5号 6号 7号 8号 9号
仰卧起坐个数 52 56 50 50 48 58 52 50 54
A.众数是58,中位数是48
B.众数是58,中位数是52
C.众数是50,中位数是48
D.众数是50,中位数是52
3.在一次捐款活动中,5名同学的捐款数分别为10,6,12,10,20(单位:元),捐20元的同学又追加了20元,追加后的5个数据与之前的5个数据相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
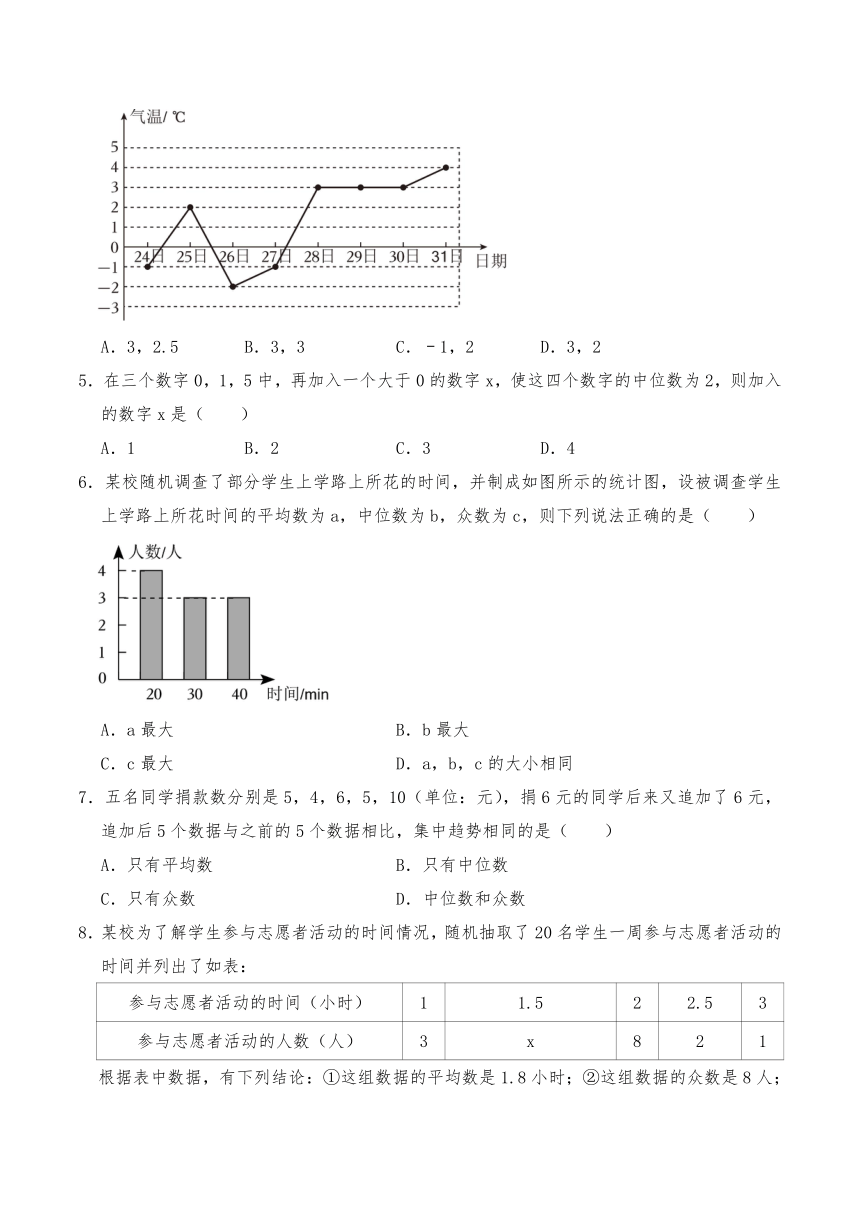
4.如图是在2023年12月28日预报的我区2024年1月24日到31日八天的最低气温(℃)统计图,这八天最低气温的众数和中位数为( )
A.3,2.5 B.3,3 C.﹣1,2 D.3,2
5.在三个数字0,1,5中,再加入一个大于0的数字x,使这四个数字的中位数为2,则加入的数字x是( )
A.1 B.2 C.3 D.4
6.某校随机调查了部分学生上学路上所花的时间,并制成如图所示的统计图,设被调查学生上学路上所花时间的平均数为a,中位数为b,众数为c,则下列说法正确的是( )
A.a最大 B.b最大
C.c最大 D.a,b,c的大小相同
7.五名同学捐款数分别是5,4,6,5,10(单位:元),捐6元的同学后来又追加了6元,追加后5个数据与之前的5个数据相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
8.某校为了解学生参与志愿者活动的时间情况,随机抽取了20名学生一周参与志愿者活动的时间并列出了如表:
参与志愿者活动的时间(小时) 1 1.5 2 2.5 3
参与志愿者活动的人数(人) 3 x 8 2 1
根据表中数据,有下列结论:①这组数据的平均数是1.8小时;②这组数据的众数是8人;③这组数据的中位数是2小时;④若该校共有500名学生,则每周参与志愿者活动的时间不少于2.5小时的学生约有70人.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.家务劳动是中学生的一项重要生活技能.某校为了解七年级学生平均每周在家的劳动时间,随机抽取了部分七年级学生进行调查,根据调查结果,绘制了如下频数分布表:
组别 一 二 三 四
劳动时间x/h 0≤x<1 1≤x<2 2≤x<3 x≥3
频数 10 20 12 8
根据表中的信息,下列说法正确的是( )
A.本次调查的样本容量是60
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组
C.本次调查七年级学生平均每周在家劳动时间的众数落在三组
D.若七年级共有500名学生,则平均每周在家劳动时间不少于2 h的学生约有100人
10.若3个正数a1,a2,a3的平均数是a,且a1>a2>a3,则数据a1,a2,0,a3的平均数和中位数是( )
A.a1,a2 B.
C. D.
二、填空题
11.样本数据﹣1,4,7,a的中位数与平均数相同,则a的值是 .
12.某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的中位数是 台.
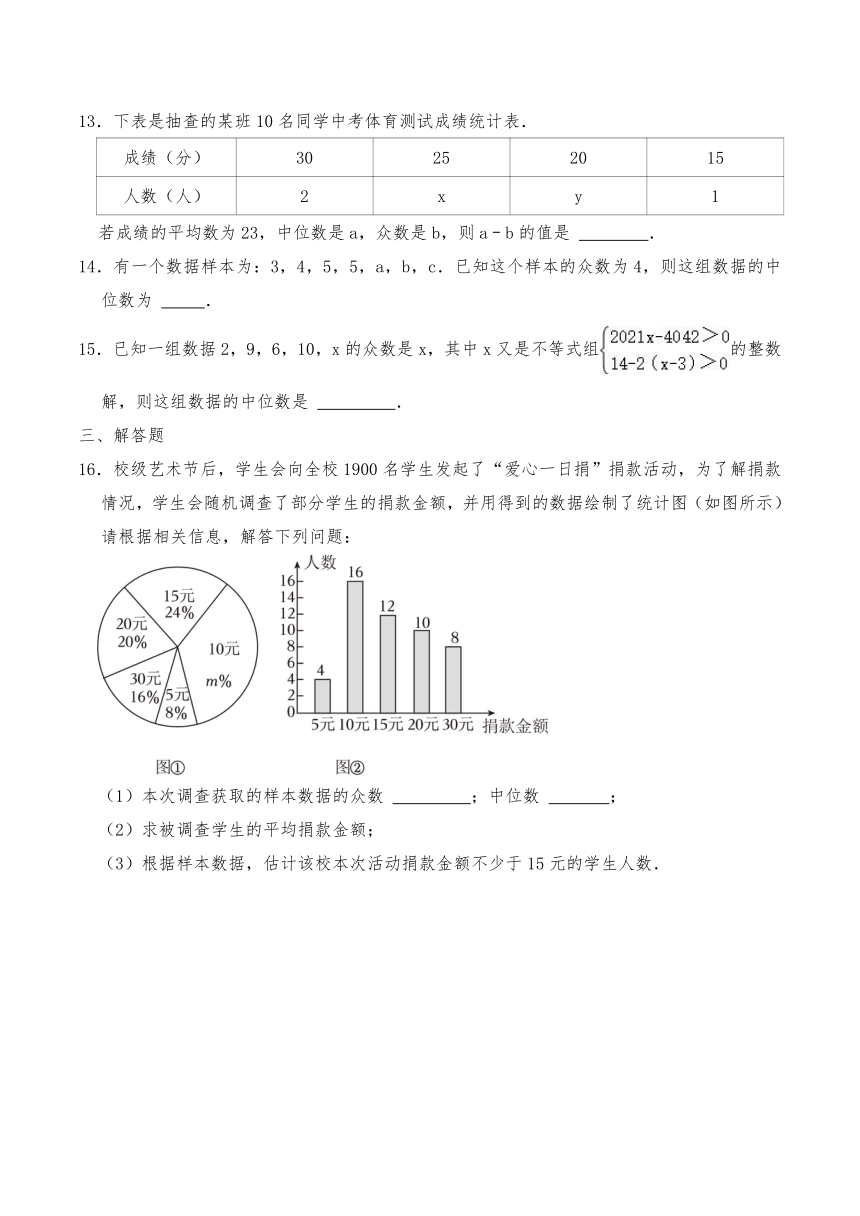
13.下表是抽查的某班10名同学中考体育测试成绩统计表.
成绩(分) 30 25 20 15
人数(人) 2 x y 1
若成绩的平均数为23,中位数是a,众数是b,则a﹣b的值是 .
14.有一个数据样本为:3,4,5,5,a,b,c.已知这个样本的众数为4,则这组数据的中位数为 .
15.已知一组数据2,9,6,10,x的众数是x,其中x又是不等式组的整数解,则这组数据的中位数是 .
三、解答题
16.校级艺术节后,学生会向全校1900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了统计图(如图所示)请根据相关信息,解答下列问题:
(1)本次调查获取的样本数据的众数 ;中位数 ;
(2)求被调查学生的平均捐款金额;
(3)根据样本数据,估计该校本次活动捐款金额不少于15元的学生人数.
17.为宣传6月8日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级700名学生此次竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).
组别 分数/分 频数组 内学生的平均成绩/分
A 60≤x<70 a 65
B 70≤x<80 10 75
C 80≤x<90 14 85
D 90≤x≤100 18 95
请根据图表信息,解答以下问题:
(1)一共抽取了 人,表中a= ,所抽取参赛学生的成绩的中位数落在“组别” ;
(2)求所抽取的这些学生的平均成绩;
(3)请你估计该校九年级竞赛成绩达到90分及以上的学生约有多少人?
18.交警部门在一个路口对某个时段来往的车辆的车速进行监测(假设监测车速均为整数),统计数据如下表:
车速(km/h) 40 41 42 43 44 45
频数 6 8 15 a 3 2
其中车速为40.43(单位:km/h)的车辆数分别占监测的车辆总数的12%、32%.
(1)求出表格中a的值;
(2)结合调查,估计该路口此时段车速的中位数是 km/h;
(3)如果一辆汽车行驶的车速不超过44km/h时,就认定这辆车安全行驶.若一年内在该时段通过此路口的车辆有20000辆,试估计其中安全行驶的车辆数.
19.跳绳是驿城区某校体育活动的特色项目.体育组为了了解八年级学生1分钟跳绳次数情况,随机抽取20名八年级学生进行1分钟跳绳测试(单位:次),数据如下:
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析,结果如下:
平均数 众数 中位数
145 a b
请根据以上信息解答下列问题:
(1)填空:a= ,b= .
(2)学校规定1分钟跳绳165次及以上为优秀,请你估计七年级500名学生中,约有多少名学生能达到优秀.
(3)某同学1分钟跳绳152次,请推测该同学的1分钟跳绳次数是否超过年级一半的学生?说明理由.
20.学习中国共产党百年党史,汲取奋进力量.某校利用网络平台进行党史知识测试,测试题共10道题目,每小题10分.李华同学对甲,乙两个班各40名同学的测试成绩进行了收集,整理和分析,数据如下:
①甲班成绩如下:
60,60,60,60,70,70,70,70,70,70,
70,70,70,80,80,80,80,80,80,80,
90,90,90,90,90,90,90,90,90,90,
90,90,90,100,100,100,100,100,100,100.
②乙班成绩平均分的计算过程如下:
=80.5(分)
③数据分析如下:
班级 平均数 中位数 众数
甲班 82.5 a 90
乙班 80.5 75 b
根据以上信息,解决下列问题:
(1)直接写出表中a和b的值;
(2)在本次测试中,甲班小张同学和乙班小黄同学的成绩均为80分,你认为两人在各自班级中谁的成绩排名更靠前?请说明理由;
(3)学校将给测试成绩满分的同学颁发奖状,该校八年级学生共800人,试估计需要准备多少张奖状.
答案
一、单选题
1.
【分析】将数据重新排列,再根据众数和中位数的定义求解即可.
【解答】解:将这组数据重新排列为74,76,78,78,80,80,80,85,
所以这组数据的众数为80,中位数为=79,
故选:A.
2.
【分析】根据众数和中位数的概念求解即可.
【解答】解:这组数据中50出现的次数最多,故众数为50,
先把这些数从小到大排列,第5个女生的成绩为中位数,
则中位数是52;
故选:D.
3.
【分析】根据中位数和众数的概念做出判断即可.
【解答】解:根据题意知,追加前5个数据的中位数是10,众数是10,
追加后5个数据的中位数是10,众数为10,
∵数据追加后平均数会变大,
∴集中趋势相同的只有中位数和众数,
故选:D.
4.
【分析】根据折线图得出八天的最低气温,然后根据众数和中位数的定义解答即可.
【解答】解:八天的最低气温(℃)为:﹣2,﹣1,﹣1,2,3,3,3,4,
∴众数为3,中位数为=2.5.
故选:A.
5.
【分析】在三个数字0,1,5中,再加入一个大于0的数字x,使这四个数字的中位数为2,则这四个数字是0,1,x,5,根据中位数为2求出x即可.
【解答】解:∵在三个数字0,1,5中,再加入一个大于0的数字x,使这四个数字的中位数为2,
∴这四个数字排序后是0,1,x,5,
∵中位数为2,
∴=2,
解得x=3.
故选:C.
6.
【分析】根据平均数、众数、中位数的定义解答即可.
【解答】解:∵平均数为a=(20×4+30×3+40×3)÷(4+3+3)=29,中位数b==30,众数c=20,
∴b>a>c.
∴b最大.
故选:B.
7.
【分析】根据平均数、中位数和众数的定义,分别求得两次的平均数、中位数和众数即可求解.
【解答】解:追加前的数据重新排列为4,5,5,6,10,众数为5,中位数为5,
平均数为:;
追加后的数据重新排列为4,5,5,10,12,众数为5,中位数为5,
追加后的平均数为:;
∴集中趋势相同的是中位数和众数.
故选:D.
8.
【分析】用20分别减去其它组的频数可得x的值,再分别根据加权平均数的定义、众数、中位数以及用样本估计总体解答即可.
【解答】解:由题意得x=20﹣3﹣8﹣2﹣1=6,
①这组数据的平均数是=1.8小时,正确;
②这组数据的众数是2,错误;
③这组数据的中位数是=2,正确;
④若该校共有500名学生,则每周参与志愿者活动的时间不少于2.5小时的学生约有500×=75人,错误;
其中正确的个数是2个.
故选:B.
9.
【分析】根据中位数、众数、样本估计总体的定义即可解答.
【解答】解:A、本次调查的样本容量是10+20+12+8=50,原说法错误,故本选项不符合题意.
B、本次调查七年级学生平均每周在家劳动中位数落在二组,说法正确,故本选项符合题意.
C、无法判断本次调查七年级学生平均每周在家劳动时间的众数落在哪一组,原说法错误,故本选项不符合题意.
D、若七年级共有500名学生,则平均每周在家劳动时间不少于2 h的学生约有(人),原说法错误,故本选项不符合题意.
故选:B.
10.
【分析】根据平均数和中位数的定义计算即可.
【解答】解:∵3个正数a1,a2,a3的平均数是a,
∴a1+a2+a3=3a,
∴a1,a2,0,a3的平均数为,
∵3个正数a1,a2,a3,且a1>a2>a3
∴把数据a1,a2,0,a3从大到小排列为a1,a2,a3,0,
∴中位数为,
故选:B.
二、填空题
11.
【分析】分三种情况进行讨论,①a≤﹣1,②a≥7,③﹣1<a<7,根据平均数与中位数的定义可得出a的值.
【解答】解:①当a≤﹣1时,平均数为,中位数为,
故可得:,
解得:a=﹣4.
②当a≥7时,平均数为,中位数为,
故可得:,
解得:a=12.
③当﹣1<a<7时,平均数为,中位数为,
故可得:,
解得:a=2,
故a可取﹣4或2或12.
故答案为:﹣4或2或12.
12.
【分析】根据中位数的定义作答即可.
【解答】解:把这些数从小到大排列,最中间的数是第10、11个数的平均数,
则中位数是=20(台),
故答案为:20.
13.
【分析】首先根据平均数求得x、y的值,然后利用中位数及众数的定义求得a和b的值,从而求得a﹣b的值即可.
【解答】解:∵平均数为23,
∴=23,
∴25x+20y=155,
即:5x+4y=31,
∵x+y=7,
∴x=3,y=4,
∴中位数a=22.5,b=20,
∴a﹣b=2.5.
故答案为:2.5.
14.
【分析】根据众数的定义可知a,b,c中有2个4,或3个都为4,不能是5,据此即可求解.
【解答】解:众数的定义可知a,b,c中有2个4,或3个都为4,
设a=b=4,c≠5,
则c≤4或c>5,
∴这组数据为3,c,a,b,4,5,5,或3,a,b,4,5,5,c,
则中位数为4.
故答案为:4.
15.
【分析】先求出不等式组的整数解,再根据众数的定义可求x的值,再根据中位数是排序后位于中间位置或中间两数的平均数求解.
【解答】解:,
解不等式2021x﹣4042x>0,得x>2,
解不等式14﹣2(x﹣3)>0,得x<10,
∴不等式组的解集为2<x<10,
∴不等式组的整数解是3、4、5、6、7、8、9,
∵一组数据2,9,6,10,x的众数是x,
∴x=6或9,
∴这组数据的中位数是6或9.
故答案为:6或9.
三、解答题
16.解:(1)∵捐赠10元的有16人,
∴本次调查获取的样本数据的众数为10;
∵本次接受随机抽样调查的学生有4÷8%=50(人),
∴中位数在第25和26位,
本次调查获取的样本数据的中位数为:(元);
故答案为:10,15;
(2)本次调查捐款30元的有8人,
所以本次调查获取的样本数据的平均数为:
(元);
(3)(人),
答:估计该校本次活动捐款金额不少于15元的学生有1140人.
17.解:(1)本次调查一共随机抽取学生:18÷36%=50(人),
则A组的人数a=50×16%=8(人),
本次调查一共随机抽取50名学生,第25、26位两个数都在C组,中位数落在C组,
故答案为:50,8,C;
(2)抽取的这些学生的平均成绩为:
(分),
答:所抽取的这些学生的平均成绩是83.4分;
(3)该校九年级竞赛成绩达到90分及以上的学生人数约为:
(人),
答:该校九年级竞赛成绩达到90分及以上的学生约有252人.
18.解:(1)6÷12%=50(辆),
a=50×32%=16,
(2)把车速从小到大排列,处于中间位置的是42,43,
则该路口此时段车速的中位数是=42.5,
∵监测车速均为整数,
故答案为:42;
(3)∵一辆汽车行驶的车速不超过44km/h时,
∴45km/h时不是安全行驶,
(辆),
答:安全行驶的车辆数约为19200辆.
19.解:(1)在被抽取20名八年级学生进行1分钟跳绳测试成绩中,165出现的次数最多,故众数a=165;
把被抽取20名八年级学生进行1分钟跳绳测试成绩从小到大排列,排在中间的两个数分别是148,152,故中位数b==150.
故答案为:165;150;
(2)500×=175(名),
答:估计八年级500名学生中,约有175名学生能达到优秀;
(3)超过年级一半的学生,理由如下:
∵152>150,
∴推测该同学的1分钟跳绳次数超过年级一半的学生.
20.解:(1)将甲班40名同学的测试成绩按从小到大的顺序排列后,第20、21个数据分别为80、90,
∴甲班成绩的中位数a==85(分),
由乙班平均成绩的算式知70分出现次数最多,有17次,
∴乙班成绩的众数b=70分;
(2)乙班小黄同学在班级中的成绩排名更靠前,理由如下:
因为甲班的中位数为85分,大于80分,说明本班有一半以上的同学比小张同学成绩好,而乙班的中位数为75分,小于80分,说明乙班小黄比本班一半以上的同学成绩好,
所以乙班小黄在班级的排名更靠前;
(3)800×=150(张).
故可估计需要准备150张奖状.
一、单选题
1.2024年,中国将迎来一系列重要的周年纪念活动,某校开展了主题为“牢记历史 吾辈自强”的演讲比赛,九年级8名同学参加该演讲比赛的成绩分别为76,78,80,85,80,74,78,80.则这组数据的众数和中位数分别为( )
A.80,79 B.80,78 C.78,79 D.80,80
2.金牛区某校八年级学生参加体质健康测试,有一组9个女生做一分钟的仰卧起坐个数如表中数据所示,则这组仰卧起坐个数的众数和中位数分别是( )
学生(序号) 1号 2号 3号 4号 5号 6号 7号 8号 9号
仰卧起坐个数 52 56 50 50 48 58 52 50 54
A.众数是58,中位数是48
B.众数是58,中位数是52
C.众数是50,中位数是48
D.众数是50,中位数是52
3.在一次捐款活动中,5名同学的捐款数分别为10,6,12,10,20(单位:元),捐20元的同学又追加了20元,追加后的5个数据与之前的5个数据相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
4.如图是在2023年12月28日预报的我区2024年1月24日到31日八天的最低气温(℃)统计图,这八天最低气温的众数和中位数为( )
A.3,2.5 B.3,3 C.﹣1,2 D.3,2
5.在三个数字0,1,5中,再加入一个大于0的数字x,使这四个数字的中位数为2,则加入的数字x是( )
A.1 B.2 C.3 D.4
6.某校随机调查了部分学生上学路上所花的时间,并制成如图所示的统计图,设被调查学生上学路上所花时间的平均数为a,中位数为b,众数为c,则下列说法正确的是( )
A.a最大 B.b最大
C.c最大 D.a,b,c的大小相同
7.五名同学捐款数分别是5,4,6,5,10(单位:元),捐6元的同学后来又追加了6元,追加后5个数据与之前的5个数据相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
8.某校为了解学生参与志愿者活动的时间情况,随机抽取了20名学生一周参与志愿者活动的时间并列出了如表:
参与志愿者活动的时间(小时) 1 1.5 2 2.5 3
参与志愿者活动的人数(人) 3 x 8 2 1
根据表中数据,有下列结论:①这组数据的平均数是1.8小时;②这组数据的众数是8人;③这组数据的中位数是2小时;④若该校共有500名学生,则每周参与志愿者活动的时间不少于2.5小时的学生约有70人.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.家务劳动是中学生的一项重要生活技能.某校为了解七年级学生平均每周在家的劳动时间,随机抽取了部分七年级学生进行调查,根据调查结果,绘制了如下频数分布表:
组别 一 二 三 四
劳动时间x/h 0≤x<1 1≤x<2 2≤x<3 x≥3
频数 10 20 12 8
根据表中的信息,下列说法正确的是( )
A.本次调查的样本容量是60
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组
C.本次调查七年级学生平均每周在家劳动时间的众数落在三组
D.若七年级共有500名学生,则平均每周在家劳动时间不少于2 h的学生约有100人
10.若3个正数a1,a2,a3的平均数是a,且a1>a2>a3,则数据a1,a2,0,a3的平均数和中位数是( )
A.a1,a2 B.
C. D.
二、填空题
11.样本数据﹣1,4,7,a的中位数与平均数相同,则a的值是 .
12.某电脑公司销售部为了制订下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的中位数是 台.
13.下表是抽查的某班10名同学中考体育测试成绩统计表.
成绩(分) 30 25 20 15
人数(人) 2 x y 1
若成绩的平均数为23,中位数是a,众数是b,则a﹣b的值是 .
14.有一个数据样本为:3,4,5,5,a,b,c.已知这个样本的众数为4,则这组数据的中位数为 .
15.已知一组数据2,9,6,10,x的众数是x,其中x又是不等式组的整数解,则这组数据的中位数是 .
三、解答题
16.校级艺术节后,学生会向全校1900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了统计图(如图所示)请根据相关信息,解答下列问题:
(1)本次调查获取的样本数据的众数 ;中位数 ;
(2)求被调查学生的平均捐款金额;
(3)根据样本数据,估计该校本次活动捐款金额不少于15元的学生人数.
17.为宣传6月8日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级700名学生此次竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).
组别 分数/分 频数组 内学生的平均成绩/分
A 60≤x<70 a 65
B 70≤x<80 10 75
C 80≤x<90 14 85
D 90≤x≤100 18 95
请根据图表信息,解答以下问题:
(1)一共抽取了 人,表中a= ,所抽取参赛学生的成绩的中位数落在“组别” ;
(2)求所抽取的这些学生的平均成绩;
(3)请你估计该校九年级竞赛成绩达到90分及以上的学生约有多少人?
18.交警部门在一个路口对某个时段来往的车辆的车速进行监测(假设监测车速均为整数),统计数据如下表:
车速(km/h) 40 41 42 43 44 45
频数 6 8 15 a 3 2
其中车速为40.43(单位:km/h)的车辆数分别占监测的车辆总数的12%、32%.
(1)求出表格中a的值;
(2)结合调查,估计该路口此时段车速的中位数是 km/h;
(3)如果一辆汽车行驶的车速不超过44km/h时,就认定这辆车安全行驶.若一年内在该时段通过此路口的车辆有20000辆,试估计其中安全行驶的车辆数.
19.跳绳是驿城区某校体育活动的特色项目.体育组为了了解八年级学生1分钟跳绳次数情况,随机抽取20名八年级学生进行1分钟跳绳测试(单位:次),数据如下:
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析,结果如下:
平均数 众数 中位数
145 a b
请根据以上信息解答下列问题:
(1)填空:a= ,b= .
(2)学校规定1分钟跳绳165次及以上为优秀,请你估计七年级500名学生中,约有多少名学生能达到优秀.
(3)某同学1分钟跳绳152次,请推测该同学的1分钟跳绳次数是否超过年级一半的学生?说明理由.
20.学习中国共产党百年党史,汲取奋进力量.某校利用网络平台进行党史知识测试,测试题共10道题目,每小题10分.李华同学对甲,乙两个班各40名同学的测试成绩进行了收集,整理和分析,数据如下:
①甲班成绩如下:
60,60,60,60,70,70,70,70,70,70,
70,70,70,80,80,80,80,80,80,80,
90,90,90,90,90,90,90,90,90,90,
90,90,90,100,100,100,100,100,100,100.
②乙班成绩平均分的计算过程如下:
=80.5(分)
③数据分析如下:
班级 平均数 中位数 众数
甲班 82.5 a 90
乙班 80.5 75 b
根据以上信息,解决下列问题:
(1)直接写出表中a和b的值;
(2)在本次测试中,甲班小张同学和乙班小黄同学的成绩均为80分,你认为两人在各自班级中谁的成绩排名更靠前?请说明理由;
(3)学校将给测试成绩满分的同学颁发奖状,该校八年级学生共800人,试估计需要准备多少张奖状.
答案
一、单选题
1.
【分析】将数据重新排列,再根据众数和中位数的定义求解即可.
【解答】解:将这组数据重新排列为74,76,78,78,80,80,80,85,
所以这组数据的众数为80,中位数为=79,
故选:A.
2.
【分析】根据众数和中位数的概念求解即可.
【解答】解:这组数据中50出现的次数最多,故众数为50,
先把这些数从小到大排列,第5个女生的成绩为中位数,
则中位数是52;
故选:D.
3.
【分析】根据中位数和众数的概念做出判断即可.
【解答】解:根据题意知,追加前5个数据的中位数是10,众数是10,
追加后5个数据的中位数是10,众数为10,
∵数据追加后平均数会变大,
∴集中趋势相同的只有中位数和众数,
故选:D.
4.
【分析】根据折线图得出八天的最低气温,然后根据众数和中位数的定义解答即可.
【解答】解:八天的最低气温(℃)为:﹣2,﹣1,﹣1,2,3,3,3,4,
∴众数为3,中位数为=2.5.
故选:A.
5.
【分析】在三个数字0,1,5中,再加入一个大于0的数字x,使这四个数字的中位数为2,则这四个数字是0,1,x,5,根据中位数为2求出x即可.
【解答】解:∵在三个数字0,1,5中,再加入一个大于0的数字x,使这四个数字的中位数为2,
∴这四个数字排序后是0,1,x,5,
∵中位数为2,
∴=2,
解得x=3.
故选:C.
6.
【分析】根据平均数、众数、中位数的定义解答即可.
【解答】解:∵平均数为a=(20×4+30×3+40×3)÷(4+3+3)=29,中位数b==30,众数c=20,
∴b>a>c.
∴b最大.
故选:B.
7.
【分析】根据平均数、中位数和众数的定义,分别求得两次的平均数、中位数和众数即可求解.
【解答】解:追加前的数据重新排列为4,5,5,6,10,众数为5,中位数为5,
平均数为:;
追加后的数据重新排列为4,5,5,10,12,众数为5,中位数为5,
追加后的平均数为:;
∴集中趋势相同的是中位数和众数.
故选:D.
8.
【分析】用20分别减去其它组的频数可得x的值,再分别根据加权平均数的定义、众数、中位数以及用样本估计总体解答即可.
【解答】解:由题意得x=20﹣3﹣8﹣2﹣1=6,
①这组数据的平均数是=1.8小时,正确;
②这组数据的众数是2,错误;
③这组数据的中位数是=2,正确;
④若该校共有500名学生,则每周参与志愿者活动的时间不少于2.5小时的学生约有500×=75人,错误;
其中正确的个数是2个.
故选:B.
9.
【分析】根据中位数、众数、样本估计总体的定义即可解答.
【解答】解:A、本次调查的样本容量是10+20+12+8=50,原说法错误,故本选项不符合题意.
B、本次调查七年级学生平均每周在家劳动中位数落在二组,说法正确,故本选项符合题意.
C、无法判断本次调查七年级学生平均每周在家劳动时间的众数落在哪一组,原说法错误,故本选项不符合题意.
D、若七年级共有500名学生,则平均每周在家劳动时间不少于2 h的学生约有(人),原说法错误,故本选项不符合题意.
故选:B.
10.
【分析】根据平均数和中位数的定义计算即可.
【解答】解:∵3个正数a1,a2,a3的平均数是a,
∴a1+a2+a3=3a,
∴a1,a2,0,a3的平均数为,
∵3个正数a1,a2,a3,且a1>a2>a3
∴把数据a1,a2,0,a3从大到小排列为a1,a2,a3,0,
∴中位数为,
故选:B.
二、填空题
11.
【分析】分三种情况进行讨论,①a≤﹣1,②a≥7,③﹣1<a<7,根据平均数与中位数的定义可得出a的值.
【解答】解:①当a≤﹣1时,平均数为,中位数为,
故可得:,
解得:a=﹣4.
②当a≥7时,平均数为,中位数为,
故可得:,
解得:a=12.
③当﹣1<a<7时,平均数为,中位数为,
故可得:,
解得:a=2,
故a可取﹣4或2或12.
故答案为:﹣4或2或12.
12.
【分析】根据中位数的定义作答即可.
【解答】解:把这些数从小到大排列,最中间的数是第10、11个数的平均数,
则中位数是=20(台),
故答案为:20.
13.
【分析】首先根据平均数求得x、y的值,然后利用中位数及众数的定义求得a和b的值,从而求得a﹣b的值即可.
【解答】解:∵平均数为23,
∴=23,
∴25x+20y=155,
即:5x+4y=31,
∵x+y=7,
∴x=3,y=4,
∴中位数a=22.5,b=20,
∴a﹣b=2.5.
故答案为:2.5.
14.
【分析】根据众数的定义可知a,b,c中有2个4,或3个都为4,不能是5,据此即可求解.
【解答】解:众数的定义可知a,b,c中有2个4,或3个都为4,
设a=b=4,c≠5,
则c≤4或c>5,
∴这组数据为3,c,a,b,4,5,5,或3,a,b,4,5,5,c,
则中位数为4.
故答案为:4.
15.
【分析】先求出不等式组的整数解,再根据众数的定义可求x的值,再根据中位数是排序后位于中间位置或中间两数的平均数求解.
【解答】解:,
解不等式2021x﹣4042x>0,得x>2,
解不等式14﹣2(x﹣3)>0,得x<10,
∴不等式组的解集为2<x<10,
∴不等式组的整数解是3、4、5、6、7、8、9,
∵一组数据2,9,6,10,x的众数是x,
∴x=6或9,
∴这组数据的中位数是6或9.
故答案为:6或9.
三、解答题
16.解:(1)∵捐赠10元的有16人,
∴本次调查获取的样本数据的众数为10;
∵本次接受随机抽样调查的学生有4÷8%=50(人),
∴中位数在第25和26位,
本次调查获取的样本数据的中位数为:(元);
故答案为:10,15;
(2)本次调查捐款30元的有8人,
所以本次调查获取的样本数据的平均数为:
(元);
(3)(人),
答:估计该校本次活动捐款金额不少于15元的学生有1140人.
17.解:(1)本次调查一共随机抽取学生:18÷36%=50(人),
则A组的人数a=50×16%=8(人),
本次调查一共随机抽取50名学生,第25、26位两个数都在C组,中位数落在C组,
故答案为:50,8,C;
(2)抽取的这些学生的平均成绩为:
(分),
答:所抽取的这些学生的平均成绩是83.4分;
(3)该校九年级竞赛成绩达到90分及以上的学生人数约为:
(人),
答:该校九年级竞赛成绩达到90分及以上的学生约有252人.
18.解:(1)6÷12%=50(辆),
a=50×32%=16,
(2)把车速从小到大排列,处于中间位置的是42,43,
则该路口此时段车速的中位数是=42.5,
∵监测车速均为整数,
故答案为:42;
(3)∵一辆汽车行驶的车速不超过44km/h时,
∴45km/h时不是安全行驶,
(辆),
答:安全行驶的车辆数约为19200辆.
19.解:(1)在被抽取20名八年级学生进行1分钟跳绳测试成绩中,165出现的次数最多,故众数a=165;
把被抽取20名八年级学生进行1分钟跳绳测试成绩从小到大排列,排在中间的两个数分别是148,152,故中位数b==150.
故答案为:165;150;
(2)500×=175(名),
答:估计八年级500名学生中,约有175名学生能达到优秀;
(3)超过年级一半的学生,理由如下:
∵152>150,
∴推测该同学的1分钟跳绳次数超过年级一半的学生.
20.解:(1)将甲班40名同学的测试成绩按从小到大的顺序排列后,第20、21个数据分别为80、90,
∴甲班成绩的中位数a==85(分),
由乙班平均成绩的算式知70分出现次数最多,有17次,
∴乙班成绩的众数b=70分;
(2)乙班小黄同学在班级中的成绩排名更靠前,理由如下:
因为甲班的中位数为85分,大于80分,说明本班有一半以上的同学比小张同学成绩好,而乙班的中位数为75分,小于80分,说明乙班小黄比本班一半以上的同学成绩好,
所以乙班小黄在班级的排名更靠前;
(3)800×=150(张).
故可估计需要准备150张奖状.
