27.3 第2课时 位似变换与坐标 教学设计 人教版(2024)数学九年级下册
文档属性
| 名称 | 27.3 第2课时 位似变换与坐标 教学设计 人教版(2024)数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 12:56:25 | ||
图片预览


文档简介
27.3 位 似第2课时 位似变换与坐标
第2课时 位似变换与坐标
教学目标:
1.能熟练地利用坐标变化将一个图形放大与缩小;了解四种图形变换(平移、轴对称、旋转和位似)的异同.
2.在具体活动操作中,培养学生的动手操作能力,进一步增强用位似变换来解决实际问题的能力.
3.在观察、操作、推理、归纳等探索过程中,进一步培养学生综合运用知识的能力,体验成功的喜悦,树立良好的数学自信心.
教学重难点:
重点:用图形的坐标变化来表示图形的位似变换,能综合运用平移、轴对称、旋转和位似进行图案设计.
难点:用图形的坐标变化来表示图形的位似变换.
教学过程:
导入
问题:将如图(1)所示的图形如何变换得到如图(2)所示的图形
讲授新课
在平面直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么位似是否也可以用两个图形坐标之间的关系来表示呢
知识点1 平面直角坐标系中的位似变换
合作探究
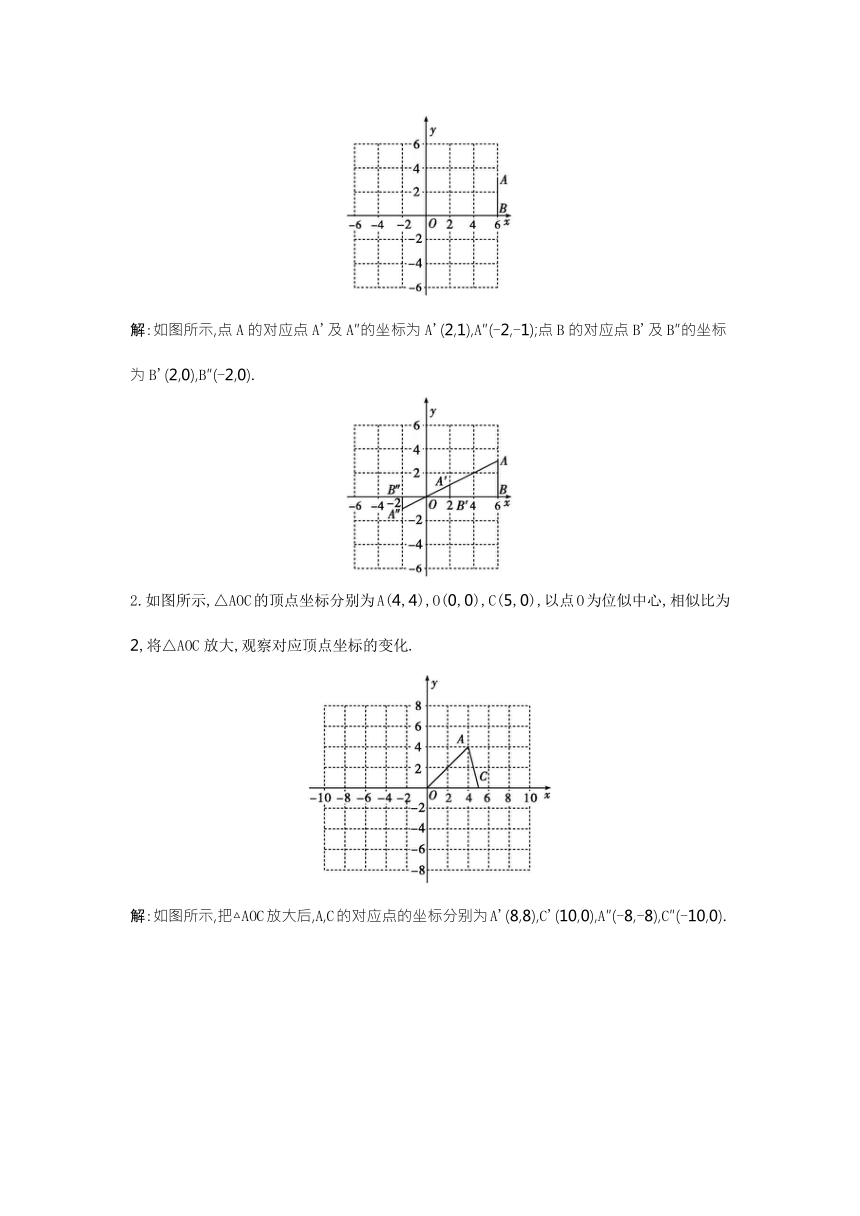
1.如图所示,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化.
解:如图所示,点A的对应点A'及A″的坐标为A'(2,1),A″(-2,-1);点B的对应点B'及B″的坐标为B'(2,0),B″(-2,0).
2.如图所示,△AOC的顶点坐标分别为A(4,4),O(0,0),C(5,0),以点O为位似中心,相似比为2,将△AOC放大,观察对应顶点坐标的变化.
解:如图所示,把△AOC放大后,A,C的对应点的坐标分别为A'(8,8),C'(10,0),A″(-8,-8),C″(-10,0).
问题1:在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个
问题2:如果所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系 如果所作位似图形与原图形在原点的异侧呢
问题3:如何在平面直角坐标系中,以原点为位似中心,画一个图形的位似图形
[设计意图] 通过对上述问题的探究思考,让学生主动参与数学知识的“再发现”,在动手—猜想—交流—归纳过程中进一步体验坐标平面内的位似变换性质.
[归纳总结] (1)在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个;
(2)当位似图形在原点同侧时,其对应顶点的坐标的比为k;当位似图形在原点异侧时,其对应顶点的坐标的比为-k,即原图形上点的坐标为(x,y),则对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky);
(3)当k>1时,图形扩大为原来的k倍;当0范例应用
例1 如图所示,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点D的坐标为(D)
A.(2,2) B.(2,1) C.(3,2) D.(3,1)
例2 △ABC三个顶点的坐标分别为A(3,6),B(6,2),C(2,-1),以原点为位似中心,得到的位似图形△A'B'C'三个顶点坐标分别为A'(1,2),B'(2,),C'(,-),则△A'B'C'与△ABC的相似比是 1∶3 .
例3 如图所示,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0).以原点O为位似中心,在△ABO的同一侧画出一个三角形使它与△ABO的相似比为3∶2.
解:如图所示,△A'B'O即为所求.
知识点2 平面直角坐标系中的图形变换
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗 在如图所示的图案中,你能找到这些变换吗
试一试:将图中的△ABC做下列变换,画出相应的图形.(每个小方格的边长为1个单位长度)
(1)沿y轴向上平移3个单位长度;
(2)关于x轴对称;
(3)在点C的左侧,以C点为位似中心,画一个三角形使它与△ABC的相似比为2∶1;
(4)以C为中心,将△ABC顺时针旋转180°.
解:(1)如图①所示.
(2)如图②所示.
(3)如图③所示.
(4)如图④所示.
课堂训练
1.如图所示,每个小方格的边长为1个单位长度,将△ABC的三边分别扩大为原来的2倍得到△A1B1C1(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是(D)
A.(-3,-3) B.(-3,-4) C.(-4,-4) D.(-4,-3)
2.如图所示,点A的坐标为(3,4),点O的坐标为(0,0),点B的坐标为(4,0).
(1)将△AOB沿x轴向左平移1个单位长度后得△A1O1B1,则点A1的坐标为 (2,4) ,△A1O1B1的面积为 8 ;
(2)将△AOB绕原点旋转180°后得△A2OB2,则点A2的坐标为 (-3,-4) ;
(3)将△AOB沿x轴翻折后得△A3OB3,则点A3的坐标为 (3,-4) ;
(4)以O为位似中心,将△AOB放大后得△A4OB4,相似比为1∶2,若点B4在x轴负半轴上,则点A4的坐标为 (-6,-8) ,△A4OB4的面积为 32 .
3.如图所示,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点B的对应点B'的横坐标是a,求点B的横坐标.
解:如图所示,作BE垂直于x轴于点E,B'F垂直于x轴于点F,
则△BEC∽△B'FC.
因为△ABC与△A'B'C的相似比为1∶2,
所以B'C=2BC.
所以2EC=CF.设点B的横坐标为x,
即2(-x-1)=a+1.
所以x=-(a+3)=-a-.
即点B的横坐标为-a-.
小结
谈谈这节课你的收获.
本节课探究平面直角坐标系上的位似图形,结合平面直角坐标系的特点可以快速推理出相似图形的点的坐标的变化规律:原图形上点的坐标为(x,y),则对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
板书
第2课时 位似变换与坐标
1.平面直角坐标系中的位似变换.
(1)坐标变化规律:(x,y)→(kx,ky)或(-kx,-ky);
(2)平面直角坐标系中的位似图形的画法.
2.平面直角坐标系中的图形变换.
反思
本课时可类比上一课时的教学方式进行,只不过本课时涉及了平面直角坐标系,教学时教师应让学生充分参与,体会平面直角坐标系中的位似变换,以培养学生的动手操作能力和用位似变换解决实际问题的能力.本课时的难点是用图形的坐标变化来表示图形的位似变换的变化规律,教师可以让学生以小组为单位进行讨论,争取让学生自己发现规律,教师再予以适当点拨,以培养学生的探究能力.
第2课时 位似变换与坐标
教学目标:
1.能熟练地利用坐标变化将一个图形放大与缩小;了解四种图形变换(平移、轴对称、旋转和位似)的异同.
2.在具体活动操作中,培养学生的动手操作能力,进一步增强用位似变换来解决实际问题的能力.
3.在观察、操作、推理、归纳等探索过程中,进一步培养学生综合运用知识的能力,体验成功的喜悦,树立良好的数学自信心.
教学重难点:
重点:用图形的坐标变化来表示图形的位似变换,能综合运用平移、轴对称、旋转和位似进行图案设计.
难点:用图形的坐标变化来表示图形的位似变换.
教学过程:
导入
问题:将如图(1)所示的图形如何变换得到如图(2)所示的图形
讲授新课
在平面直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么位似是否也可以用两个图形坐标之间的关系来表示呢
知识点1 平面直角坐标系中的位似变换
合作探究
1.如图所示,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化.
解:如图所示,点A的对应点A'及A″的坐标为A'(2,1),A″(-2,-1);点B的对应点B'及B″的坐标为B'(2,0),B″(-2,0).
2.如图所示,△AOC的顶点坐标分别为A(4,4),O(0,0),C(5,0),以点O为位似中心,相似比为2,将△AOC放大,观察对应顶点坐标的变化.
解:如图所示,把△AOC放大后,A,C的对应点的坐标分别为A'(8,8),C'(10,0),A″(-8,-8),C″(-10,0).
问题1:在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个
问题2:如果所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系 如果所作位似图形与原图形在原点的异侧呢
问题3:如何在平面直角坐标系中,以原点为位似中心,画一个图形的位似图形
[设计意图] 通过对上述问题的探究思考,让学生主动参与数学知识的“再发现”,在动手—猜想—交流—归纳过程中进一步体验坐标平面内的位似变换性质.
[归纳总结] (1)在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个;
(2)当位似图形在原点同侧时,其对应顶点的坐标的比为k;当位似图形在原点异侧时,其对应顶点的坐标的比为-k,即原图形上点的坐标为(x,y),则对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky);
(3)当k>1时,图形扩大为原来的k倍;当0
例1 如图所示,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点D的坐标为(D)
A.(2,2) B.(2,1) C.(3,2) D.(3,1)
例2 △ABC三个顶点的坐标分别为A(3,6),B(6,2),C(2,-1),以原点为位似中心,得到的位似图形△A'B'C'三个顶点坐标分别为A'(1,2),B'(2,),C'(,-),则△A'B'C'与△ABC的相似比是 1∶3 .
例3 如图所示,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0).以原点O为位似中心,在△ABO的同一侧画出一个三角形使它与△ABO的相似比为3∶2.
解:如图所示,△A'B'O即为所求.
知识点2 平面直角坐标系中的图形变换
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗 在如图所示的图案中,你能找到这些变换吗
试一试:将图中的△ABC做下列变换,画出相应的图形.(每个小方格的边长为1个单位长度)
(1)沿y轴向上平移3个单位长度;
(2)关于x轴对称;
(3)在点C的左侧,以C点为位似中心,画一个三角形使它与△ABC的相似比为2∶1;
(4)以C为中心,将△ABC顺时针旋转180°.
解:(1)如图①所示.
(2)如图②所示.
(3)如图③所示.
(4)如图④所示.
课堂训练
1.如图所示,每个小方格的边长为1个单位长度,将△ABC的三边分别扩大为原来的2倍得到△A1B1C1(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是(D)
A.(-3,-3) B.(-3,-4) C.(-4,-4) D.(-4,-3)
2.如图所示,点A的坐标为(3,4),点O的坐标为(0,0),点B的坐标为(4,0).
(1)将△AOB沿x轴向左平移1个单位长度后得△A1O1B1,则点A1的坐标为 (2,4) ,△A1O1B1的面积为 8 ;
(2)将△AOB绕原点旋转180°后得△A2OB2,则点A2的坐标为 (-3,-4) ;
(3)将△AOB沿x轴翻折后得△A3OB3,则点A3的坐标为 (3,-4) ;
(4)以O为位似中心,将△AOB放大后得△A4OB4,相似比为1∶2,若点B4在x轴负半轴上,则点A4的坐标为 (-6,-8) ,△A4OB4的面积为 32 .
3.如图所示,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点B的对应点B'的横坐标是a,求点B的横坐标.
解:如图所示,作BE垂直于x轴于点E,B'F垂直于x轴于点F,
则△BEC∽△B'FC.
因为△ABC与△A'B'C的相似比为1∶2,
所以B'C=2BC.
所以2EC=CF.设点B的横坐标为x,
即2(-x-1)=a+1.
所以x=-(a+3)=-a-.
即点B的横坐标为-a-.
小结
谈谈这节课你的收获.
本节课探究平面直角坐标系上的位似图形,结合平面直角坐标系的特点可以快速推理出相似图形的点的坐标的变化规律:原图形上点的坐标为(x,y),则对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
板书
第2课时 位似变换与坐标
1.平面直角坐标系中的位似变换.
(1)坐标变化规律:(x,y)→(kx,ky)或(-kx,-ky);
(2)平面直角坐标系中的位似图形的画法.
2.平面直角坐标系中的图形变换.
反思
本课时可类比上一课时的教学方式进行,只不过本课时涉及了平面直角坐标系,教学时教师应让学生充分参与,体会平面直角坐标系中的位似变换,以培养学生的动手操作能力和用位似变换解决实际问题的能力.本课时的难点是用图形的坐标变化来表示图形的位似变换的变化规律,教师可以让学生以小组为单位进行讨论,争取让学生自己发现规律,教师再予以适当点拨,以培养学生的探究能力.
