2024-2025北师大八年级下数学 第六章 平行四边形 单元测试卷(含答案)
文档属性
| 名称 | 2024-2025北师大八年级下数学 第六章 平行四边形 单元测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览


文档简介
第六章平行四边形测试卷
(时间:120分钟 满分:120分)
一、选择题(本大题共 10 小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.平行四边形具有而非平行四边形的图形不具有的性质是 ( )
A.内角和与外角和都是 360°
B.不稳定性
C.对角线互相平分
D.最多有三个钝角
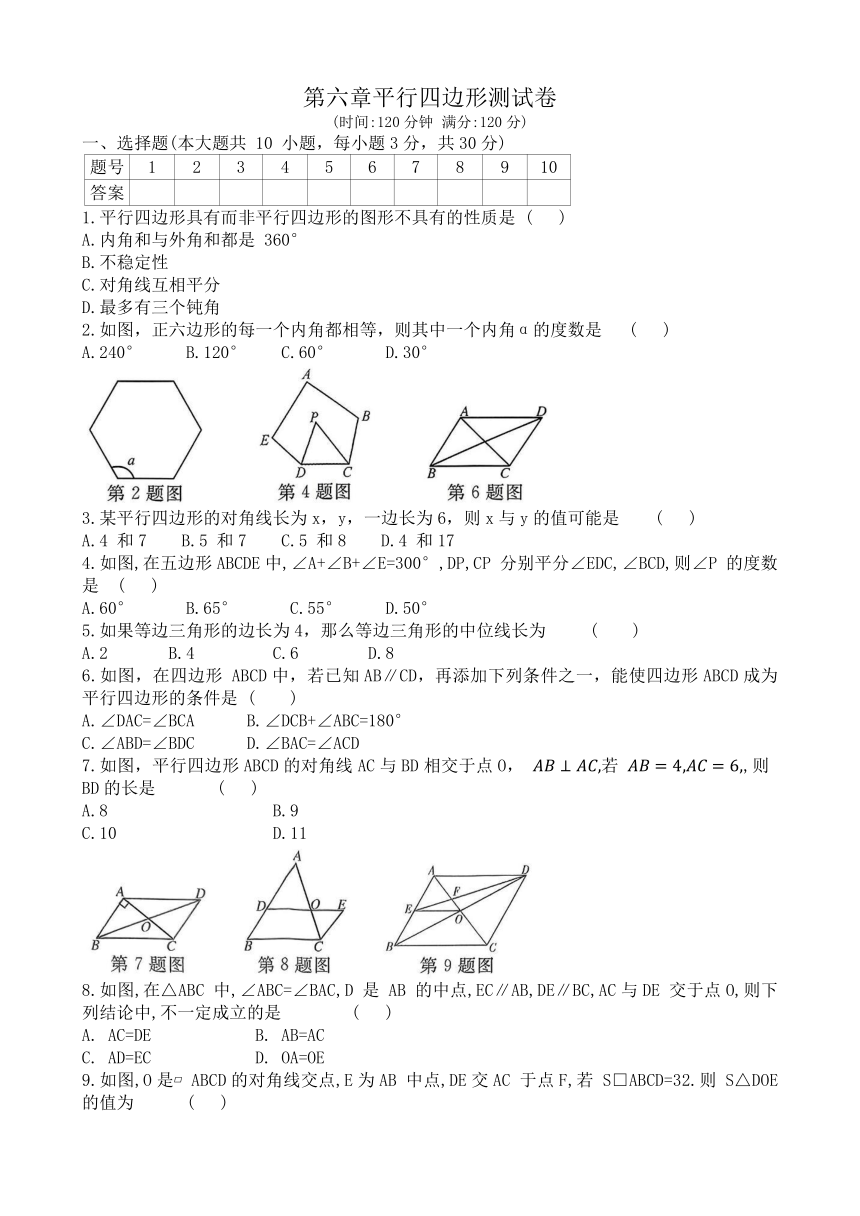
2.如图,正六边形的每一个内角都相等,则其中一个内角α的度数是 ( )
A.240° B.120° C.60° D.30°
3.某平行四边形的对角线长为x,y,一边长为6,则x与y的值可能是 ( )
A.4 和7 B.5 和7 C.5 和8 D.4 和17
4.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是 ( )
A.60° B.65° C.55° D.50°
5.如果等边三角形的边长为4,那么等边三角形的中位线长为 ( )
A.2 B.4 C.6 D.8
6.如图,在四边形 ABCD中,若已知AB∥CD,再添加下列条件之一,能使四边形ABCD成为平行四边形的条件是 ( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
7.如图,平行四边形ABCD的对角线AC与BD相交于点O, 若 ,则 BD的长是 ( )
A.8 B.9
C.10 D.11
8.如图,在△ABC 中,∠ABC=∠BAC,D 是 AB 的中点,EC∥AB,DE∥BC,AC与DE 交于点O,则下列结论中,不一定成立的是 ( )
A. AC=DE B. AB=AC
C. AD=EC D. OA=OE
9.如图,O是 ABCD的对角线交点,E为AB 中点,DE交AC 于点F,若 S□ABCD=32.则 S△DOE的值为 ( )
A.2 B.3
C.4 D.4.5
10.如图,点 E 是 ABCD的边CD 的中点,AD,BE的延长线相交于点 F,DF=3,DE=2,则 ABCD的周长为( )
A.5 B.7
C.10 D.14
二、填空题(本大题共5小题,每小题3分,共15分)
11.一个正多边形的外角为45°,则这个正多边形的边数是 .
12.如图所示,在 ABCD中,E,F分别为AD,BC边上的一点,若添加一个条件 ,则四边形 EBFD为平行四边形.
13.如图, ABCD的对角线AC,BD交于点O,点 E 是AD的中点,△BCD的周长为18,则△DEO的周长是 .
14.如图,顺次连接四边形 ABCD 四边的中点E,F,G,H,则四边形 EFGH 的形状一定是 .
15.如图, 的对角线 AC、BD 交于点O,DE 平分 交AB 于点 E, 连接OE.下列 4 个结论:①S□ABCD =AD·BD;②DB 平分∠CDE;③AO=DE;④OE 垂直平分BD.其中正确的是
三、解答题(本大题共8 小题,共75分)
16.(9分)已知一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的 ,求这个多边形的内角和.
17.(9分)如图,点 E、F 是平行四边形ABCD 对角线AC 上两点, 求证:
18.(9分)如图所示,已知∠B+∠C=150°,试求∠A+∠D+∠E+∠F的度数.
19.(9分)如图,在 ABCD中,E、F分别为AC、CA 延长线上的点,且CE=AF,请你探讨线段 BF 与DE 的位置及大小关系如何.
20.(9 分)如图,M 是△ABC的边BC 的中点,AN 平分∠BAC,BN⊥AN 于点 N,延长 BN 交AC 于点 D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ABC的周长.
21.(10分)如图,正方形网格中的每个小正方形的边长都是1, 的顶点都在格点上,用无刻度直尺完成下列作图,不写作法,保留作图痕迹.
(1)找一点 D,使以 A,B,C,D为顶点的四边形是平行四边形,并直接写出 AD的长;
(2)作出 中AB 边上的中线CE.
22.(10分)(2023·青海)如图, 是 的一个外角,
(1)尺规作图:作 的平分线,交CF于点 D(保留作图痕迹,不写作法);
(2)求证:四边形ABCD 是平行四边形.
23.(10分)如图,在四边形 ABCD 中, ,动点 P、Q 分别从 A、C 同时出发,点 P 以 的速度由 A 向 D 运动,点 Q 以 2cm /s的速度由 C向 B运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为t秒.
(分别用含有 t的式子表示);
(2)当点 P、Q与四边形ABCD 的任意两个顶点所形成的四边形是平行四边形时,求t 的值.
第六章测试卷答案
1. C 2. B 3. C 4. A 5. A 6. A 7. C 8. B 9. C 10. D
11.八 12. DE=BF 13.9 14.平行四边形 15.①②④
16.设多边形每个外角是x°,则它的每个内角是3x°,
由题意得:x+3x=180,∴x=45,∴多边形的边数是 8,
∴多边形的内角和是(8-2)×
17.平行四边形 ABCD中,AD∥BC,AD=BC, ∴∠ACB=∠CAD. 又∵BE∥DF,
∴∠BEC=∠DFA, ∴△BEC≌△DFA(AAS), ∴CE=AF.
18.图略,连接AD,设 AF,DE 交于点M,
∵∠AMD+∠DAM+∠ADM=180°,∠EMF+∠E+∠F=180°,∠AMD=∠EMF,
∴∠E+∠F=∠DAM+∠ADM, ∵∠B+∠C=150°,
∴∠BAD+∠ADC=360°-150°=210°,
∴∠BAF+∠CDE+∠E+∠F=∠BAD+∠ADC=210°.
19.线段 BF 与DE 的位置及大小关系分别是BF∥DE,BF=DE.
理由是:连接DF、BE、BD,BD交AC于点O,
∵四边形 ABCD 是平行四边形,∴OA=OC,OB=OD,∵CE=AF,∴OF=OE,
∴四边形 BFDE 是平行四边形,∴BF∥DE,BF=DE.
20.(1)利用ASA证△ANB≌△AND,从而证得 BN=DN;
(2)由(1)得AD=AB=10,再由三角形中位线定理得CD=2MN=6,从而得到△ABC 的周长为10+16+15=41.
21.(1)图略;
(2)图略.
22.(1)图略;
(2)证明:∵AB=AC,∴∠B=∠ACB,∵AD平分∠CAE,∴∠CAD=∠EAD,
∵∠CAE=∠B+∠ACB,即∠CAD + ∠EAD = ∠B +∠ACB,∴∠EAD=∠B,
∴AD∥BC,∵AB∥CD,∴四边形 ABCD 是平行四边形.
23.(1)t cm 2t cm
(2)①设t 秒后四边形ABQP 是平行四边形;
根据题意得:AP= tcm,CQ=2tcm,则 BQ=(10-2t) cm;
∵AD∥BC,∴当AP=BQ时,四边形ABQP 是平行四边形,
∴t=10-2t,解得: ,即 时四边形 ABQP 是平行四边形;
②当四边形 DCQP 是平行四边形,根据题意得:AP= xcm,CQ=2xcm,则 PD=(6-x) cm;
∵AD∥BC,∴当DP=CQ时,四边形 DCQP 是平行四边形,∴6-x=2x,解得:x=2,
③当 PD=BQ时,四边形 PBQD是平行四边形,6-x=10-2x,解得:x=4,
∴t=2或 或4秒时,点 P、Q能与四边形 ABCD 的任意两个顶点形成一个平行四边形.
(时间:120分钟 满分:120分)
一、选择题(本大题共 10 小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.平行四边形具有而非平行四边形的图形不具有的性质是 ( )
A.内角和与外角和都是 360°
B.不稳定性
C.对角线互相平分
D.最多有三个钝角
2.如图,正六边形的每一个内角都相等,则其中一个内角α的度数是 ( )
A.240° B.120° C.60° D.30°
3.某平行四边形的对角线长为x,y,一边长为6,则x与y的值可能是 ( )
A.4 和7 B.5 和7 C.5 和8 D.4 和17
4.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是 ( )
A.60° B.65° C.55° D.50°
5.如果等边三角形的边长为4,那么等边三角形的中位线长为 ( )
A.2 B.4 C.6 D.8
6.如图,在四边形 ABCD中,若已知AB∥CD,再添加下列条件之一,能使四边形ABCD成为平行四边形的条件是 ( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
7.如图,平行四边形ABCD的对角线AC与BD相交于点O, 若 ,则 BD的长是 ( )
A.8 B.9
C.10 D.11
8.如图,在△ABC 中,∠ABC=∠BAC,D 是 AB 的中点,EC∥AB,DE∥BC,AC与DE 交于点O,则下列结论中,不一定成立的是 ( )
A. AC=DE B. AB=AC
C. AD=EC D. OA=OE
9.如图,O是 ABCD的对角线交点,E为AB 中点,DE交AC 于点F,若 S□ABCD=32.则 S△DOE的值为 ( )
A.2 B.3
C.4 D.4.5
10.如图,点 E 是 ABCD的边CD 的中点,AD,BE的延长线相交于点 F,DF=3,DE=2,则 ABCD的周长为( )
A.5 B.7
C.10 D.14
二、填空题(本大题共5小题,每小题3分,共15分)
11.一个正多边形的外角为45°,则这个正多边形的边数是 .
12.如图所示,在 ABCD中,E,F分别为AD,BC边上的一点,若添加一个条件 ,则四边形 EBFD为平行四边形.
13.如图, ABCD的对角线AC,BD交于点O,点 E 是AD的中点,△BCD的周长为18,则△DEO的周长是 .
14.如图,顺次连接四边形 ABCD 四边的中点E,F,G,H,则四边形 EFGH 的形状一定是 .
15.如图, 的对角线 AC、BD 交于点O,DE 平分 交AB 于点 E, 连接OE.下列 4 个结论:①S□ABCD =AD·BD;②DB 平分∠CDE;③AO=DE;④OE 垂直平分BD.其中正确的是
三、解答题(本大题共8 小题,共75分)
16.(9分)已知一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的 ,求这个多边形的内角和.
17.(9分)如图,点 E、F 是平行四边形ABCD 对角线AC 上两点, 求证:
18.(9分)如图所示,已知∠B+∠C=150°,试求∠A+∠D+∠E+∠F的度数.
19.(9分)如图,在 ABCD中,E、F分别为AC、CA 延长线上的点,且CE=AF,请你探讨线段 BF 与DE 的位置及大小关系如何.
20.(9 分)如图,M 是△ABC的边BC 的中点,AN 平分∠BAC,BN⊥AN 于点 N,延长 BN 交AC 于点 D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ABC的周长.
21.(10分)如图,正方形网格中的每个小正方形的边长都是1, 的顶点都在格点上,用无刻度直尺完成下列作图,不写作法,保留作图痕迹.
(1)找一点 D,使以 A,B,C,D为顶点的四边形是平行四边形,并直接写出 AD的长;
(2)作出 中AB 边上的中线CE.
22.(10分)(2023·青海)如图, 是 的一个外角,
(1)尺规作图:作 的平分线,交CF于点 D(保留作图痕迹,不写作法);
(2)求证:四边形ABCD 是平行四边形.
23.(10分)如图,在四边形 ABCD 中, ,动点 P、Q 分别从 A、C 同时出发,点 P 以 的速度由 A 向 D 运动,点 Q 以 2cm /s的速度由 C向 B运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为t秒.
(分别用含有 t的式子表示);
(2)当点 P、Q与四边形ABCD 的任意两个顶点所形成的四边形是平行四边形时,求t 的值.
第六章测试卷答案
1. C 2. B 3. C 4. A 5. A 6. A 7. C 8. B 9. C 10. D
11.八 12. DE=BF 13.9 14.平行四边形 15.①②④
16.设多边形每个外角是x°,则它的每个内角是3x°,
由题意得:x+3x=180,∴x=45,∴多边形的边数是 8,
∴多边形的内角和是(8-2)×
17.平行四边形 ABCD中,AD∥BC,AD=BC, ∴∠ACB=∠CAD. 又∵BE∥DF,
∴∠BEC=∠DFA, ∴△BEC≌△DFA(AAS), ∴CE=AF.
18.图略,连接AD,设 AF,DE 交于点M,
∵∠AMD+∠DAM+∠ADM=180°,∠EMF+∠E+∠F=180°,∠AMD=∠EMF,
∴∠E+∠F=∠DAM+∠ADM, ∵∠B+∠C=150°,
∴∠BAD+∠ADC=360°-150°=210°,
∴∠BAF+∠CDE+∠E+∠F=∠BAD+∠ADC=210°.
19.线段 BF 与DE 的位置及大小关系分别是BF∥DE,BF=DE.
理由是:连接DF、BE、BD,BD交AC于点O,
∵四边形 ABCD 是平行四边形,∴OA=OC,OB=OD,∵CE=AF,∴OF=OE,
∴四边形 BFDE 是平行四边形,∴BF∥DE,BF=DE.
20.(1)利用ASA证△ANB≌△AND,从而证得 BN=DN;
(2)由(1)得AD=AB=10,再由三角形中位线定理得CD=2MN=6,从而得到△ABC 的周长为10+16+15=41.
21.(1)图略;
(2)图略.
22.(1)图略;
(2)证明:∵AB=AC,∴∠B=∠ACB,∵AD平分∠CAE,∴∠CAD=∠EAD,
∵∠CAE=∠B+∠ACB,即∠CAD + ∠EAD = ∠B +∠ACB,∴∠EAD=∠B,
∴AD∥BC,∵AB∥CD,∴四边形 ABCD 是平行四边形.
23.(1)t cm 2t cm
(2)①设t 秒后四边形ABQP 是平行四边形;
根据题意得:AP= tcm,CQ=2tcm,则 BQ=(10-2t) cm;
∵AD∥BC,∴当AP=BQ时,四边形ABQP 是平行四边形,
∴t=10-2t,解得: ,即 时四边形 ABQP 是平行四边形;
②当四边形 DCQP 是平行四边形,根据题意得:AP= xcm,CQ=2xcm,则 PD=(6-x) cm;
∵AD∥BC,∴当DP=CQ时,四边形 DCQP 是平行四边形,∴6-x=2x,解得:x=2,
③当 PD=BQ时,四边形 PBQD是平行四边形,6-x=10-2x,解得:x=4,
∴t=2或 或4秒时,点 P、Q能与四边形 ABCD 的任意两个顶点形成一个平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
