期末评估检测题(无答案)2024-2025学年青岛八年级下册数学
文档属性
| 名称 | 期末评估检测题(无答案)2024-2025学年青岛八年级下册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 122.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-11 22:03:56 | ||
图片预览

文档简介
期末评估检测题
(时间 :120分钟 总分:100分)
1. 选择题(把正确答案的序号填在括号里) (每题 3 分 ,共 30分)
(1)计算的结果是( ) .
A.4 B. -4 C. ±4 D. ±2
(2)下列二次根式中 ,属于最简二次根式的是( ) .
B. 0. 3 C. a2 +3 D. ab2
(3)如图 1所示 , 四边形 ABCD 的对角线互相平分 ,要使它成为矩形 ,需要添加的条件是( ) .
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
图 1 图 2
(4)下列各式中 ,计算不正确的是( ) .
(5)不等式组的解集在数轴上表示正确的是( ) .
A. B.
C. D.
(6)如图 2所示 ,在直角坐标系中 ,将 △ABC绕点 P 旋转 180°,得到 △A1B1C1 ,则 A1 ,B1 ,C1 的坐标分别 为( ) .
A.A1 ( -4, -6) ,B1 ( -3, -3) ,C1 ( -5, -1) B.A1 ( -6, -4) ,B1 ( -3, -3) ,C1 ( -5, -1) C.A1 ( -4, -6) ,B1 ( -3, -3) ,C1 ( -1, -5) D.A1 ( -6, -4) ,B1 ( -3, -3) ,C1 ( -1, -5)
(7)下列能使等式成立的条件是( ) .
A.x≥0 B. -3C.x>3 D.x>3或 x<0
1
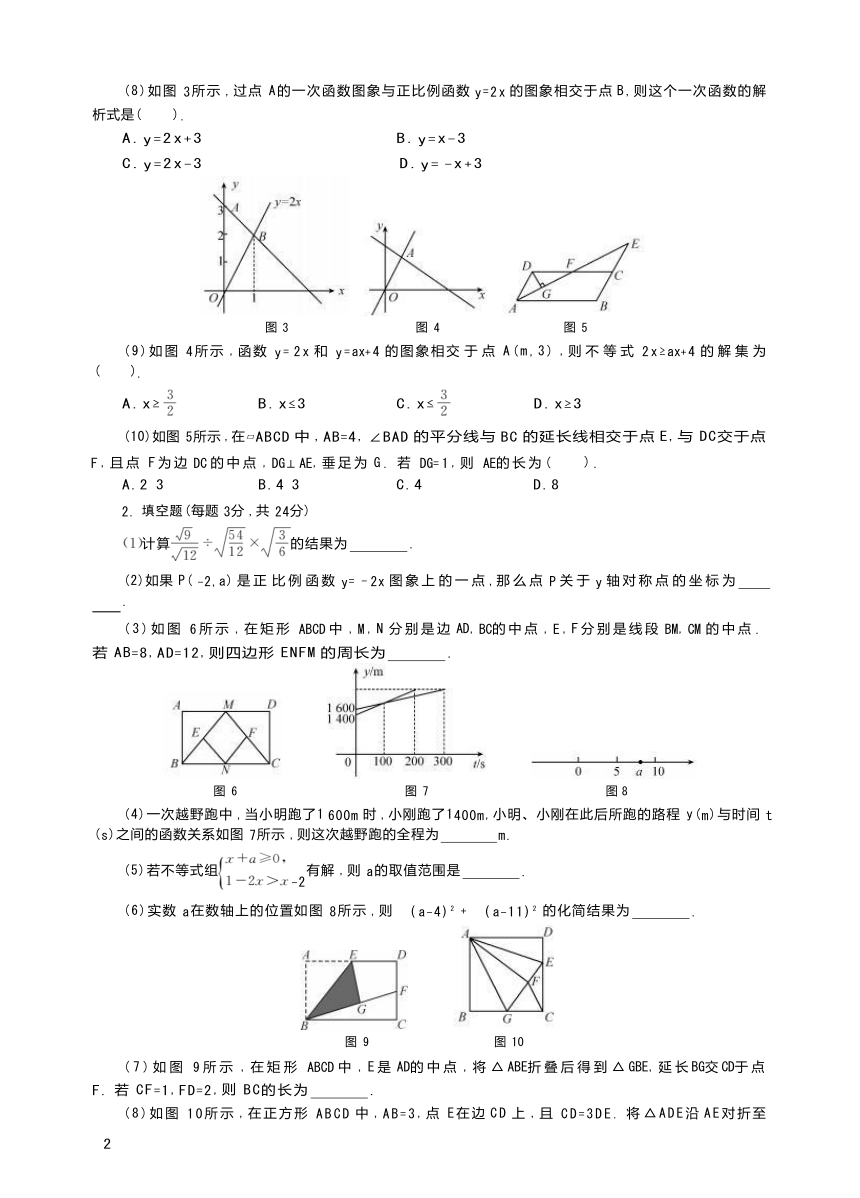
(8)如图 3所示 ,过点 A的一次函数图象与正比例函数 y=2x 的图象相交于点 B,则这个一次函数的解 析式是( ).
A.y=2x+3 B.y=x-3
C.y=2x-3 D.y= -x+3
图 3 图 4 图 5
(9)如图 4所示 ,函数 y= 2x 和 y=ax+4 的图象相交 于 点 A(m,3) ,则 不 等 式 2x≥ax+4 的 解 集 为
( ).
A.x≥ B.x≤3 C.x≤ D.x≥3
(10)如图 5所示 ,在 ABCD 中 ,AB=4, ∠BAD 的平分线与 BC 的延长线相交于点 E,与 DC交于点 F,且点 F为边 DC 的中点 ,DG⊥AE,垂足为 G. 若 DG=1,则 AE的长为( ).
A.2 3 B.4 3 C.4 D.8
2. 填空题(每题 3分 ,共 24分)
计算的结果为 .
(2)如果 P( -2,a) 是 正 比 例 函 数 y= - 2x 图 象 上 的 一 点 ,那 么 点 P 关 于 y 轴 对 称 点 的 坐 标 为
.
(3)如图 6所示 ,在矩形 ABCD 中 ,M,N 分别是边 AD,BC的中点 ,E,F分别是线段 BM,CM 的中点 . 若 AB=8,AD=12,则四边形 ENFM 的周长为 .
图 6 图 7 图 8
(4)一次越野跑中 ,当小明跑了1 600m 时 ,小刚跑了1400m,小明、小刚在此后所跑的路程 y(m)与时间 t (s)之间的函数关系如图 7所示 ,则这次越野跑的全程为 m.
(5)若不等式组-2有解 ,则 a的取值范围是 .
(6)实数 a在数轴上的位置如图 8所示 ,则 ( a-4) 2 + ( a-11) 2 的化简结果为 .
图 9 图 10
(7)如图 9所示 ,在矩形 ABCD 中 ,E是 AD的中点 ,将 △ABE折叠后得到 △GBE,延长BG交CD于点 F. 若 CF=1,FD=2,则 BC的长为 .
(8)如图 10所示 ,在正方形 ABCD 中 ,AB=3,点 E在边 CD 上 ,且 CD=3DE. 将 △ADE沿 AE对折至
2
△AFE,延长 EF交边 BC于点 G,连接 AG,CF. 下列结论:①点G是 BC 的中点 ; ②FG= FC;③SΔFGC =
其中正确的是 .
3. 解答题(共 46分)
(1) △ABC在直角坐标系中的位置如图 11所示 . (4分)
①将 △ABC向右平移 6个单位长度得到 △A1B1C1 ,画出 △A1B1C1 ,并写出点 C1 的坐标 ;
②将 △ABC绕原点 O 旋转 180°得到 △A2B2C2 ,画出 △A2B2C2 .
图 11
(2)解不等式组 ,并把它的解集在数轴上表示出来. (6分)
(3)如图 12所示 , 四边形 ABCD 的对角线 AC,BD 交于点O. 若 O是 AC的中点 ,AE=CF,DF∥BE. (8 分)
①求证 :△BOE≌△DOF;
②若 OD= 则四边形 ABCD 是什么特殊四边形 请证明你的结论 .
图 12
3
(4)如图 13所示 ,x轴所在直线是一条东西走向的河 ,A( -2, 3) ,B(4, 5) 两个村庄位于河的北岸 , 现准 备在河上修建一净水站 P,并利用管道为两个村庄供水(单位:千米) . (8分)
①欲使所修管道最短 ,应该把净水站 P 修在什么位置 ,作出正确图形(用尺规作图) ,求出点 P 的坐标及 PB所在直线的解析式 ;
②若管道每米费用需要 200元 ,求修管道的最低费用 .
图 13
(5)如图 14所示 ,点 E,F分别在正方形 ABCD 的边 CD ,BC上 , ∠EAF= 45°. (8分)
①求证 :EF=DE+BF;
②作 AP⊥EF于点 P ,若 AD= 10,求 AP 的长 .
图 14
(6)甲 、乙两商场以同样的价格出售同样的商品 ,并且又各自推出不同的优惠方案 . 在甲商场累计购物 超过 100元后 ,超出 100元的部分按 90%收费 ;在乙商场累计购物超过 50元后 ,超出 50元的部分按 95%收 费 . 设小红在同一商场累计购物 x元 ,其中x>100. (12分)
①根据题意 ,填写下表(单位 :元) .
累计购物 130 290 … x
在甲商场实际花费 127 …
在乙商场实际花费 126 …
②当 x 取何值时 ,小红在甲 、乙两商场的实际花费相同
③当小红在同一商场累计购物超过 100元时 ,在哪家商场的实际花费少
4
(时间 :120分钟 总分:100分)
1. 选择题(把正确答案的序号填在括号里) (每题 3 分 ,共 30分)
(1)计算的结果是( ) .
A.4 B. -4 C. ±4 D. ±2
(2)下列二次根式中 ,属于最简二次根式的是( ) .
B. 0. 3 C. a2 +3 D. ab2
(3)如图 1所示 , 四边形 ABCD 的对角线互相平分 ,要使它成为矩形 ,需要添加的条件是( ) .
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
图 1 图 2
(4)下列各式中 ,计算不正确的是( ) .
(5)不等式组的解集在数轴上表示正确的是( ) .
A. B.
C. D.
(6)如图 2所示 ,在直角坐标系中 ,将 △ABC绕点 P 旋转 180°,得到 △A1B1C1 ,则 A1 ,B1 ,C1 的坐标分别 为( ) .
A.A1 ( -4, -6) ,B1 ( -3, -3) ,C1 ( -5, -1) B.A1 ( -6, -4) ,B1 ( -3, -3) ,C1 ( -5, -1) C.A1 ( -4, -6) ,B1 ( -3, -3) ,C1 ( -1, -5) D.A1 ( -6, -4) ,B1 ( -3, -3) ,C1 ( -1, -5)
(7)下列能使等式成立的条件是( ) .
A.x≥0 B. -3
1
(8)如图 3所示 ,过点 A的一次函数图象与正比例函数 y=2x 的图象相交于点 B,则这个一次函数的解 析式是( ).
A.y=2x+3 B.y=x-3
C.y=2x-3 D.y= -x+3
图 3 图 4 图 5
(9)如图 4所示 ,函数 y= 2x 和 y=ax+4 的图象相交 于 点 A(m,3) ,则 不 等 式 2x≥ax+4 的 解 集 为
( ).
A.x≥ B.x≤3 C.x≤ D.x≥3
(10)如图 5所示 ,在 ABCD 中 ,AB=4, ∠BAD 的平分线与 BC 的延长线相交于点 E,与 DC交于点 F,且点 F为边 DC 的中点 ,DG⊥AE,垂足为 G. 若 DG=1,则 AE的长为( ).
A.2 3 B.4 3 C.4 D.8
2. 填空题(每题 3分 ,共 24分)
计算的结果为 .
(2)如果 P( -2,a) 是 正 比 例 函 数 y= - 2x 图 象 上 的 一 点 ,那 么 点 P 关 于 y 轴 对 称 点 的 坐 标 为
.
(3)如图 6所示 ,在矩形 ABCD 中 ,M,N 分别是边 AD,BC的中点 ,E,F分别是线段 BM,CM 的中点 . 若 AB=8,AD=12,则四边形 ENFM 的周长为 .
图 6 图 7 图 8
(4)一次越野跑中 ,当小明跑了1 600m 时 ,小刚跑了1400m,小明、小刚在此后所跑的路程 y(m)与时间 t (s)之间的函数关系如图 7所示 ,则这次越野跑的全程为 m.
(5)若不等式组-2有解 ,则 a的取值范围是 .
(6)实数 a在数轴上的位置如图 8所示 ,则 ( a-4) 2 + ( a-11) 2 的化简结果为 .
图 9 图 10
(7)如图 9所示 ,在矩形 ABCD 中 ,E是 AD的中点 ,将 △ABE折叠后得到 △GBE,延长BG交CD于点 F. 若 CF=1,FD=2,则 BC的长为 .
(8)如图 10所示 ,在正方形 ABCD 中 ,AB=3,点 E在边 CD 上 ,且 CD=3DE. 将 △ADE沿 AE对折至
2
△AFE,延长 EF交边 BC于点 G,连接 AG,CF. 下列结论:①点G是 BC 的中点 ; ②FG= FC;③SΔFGC =
其中正确的是 .
3. 解答题(共 46分)
(1) △ABC在直角坐标系中的位置如图 11所示 . (4分)
①将 △ABC向右平移 6个单位长度得到 △A1B1C1 ,画出 △A1B1C1 ,并写出点 C1 的坐标 ;
②将 △ABC绕原点 O 旋转 180°得到 △A2B2C2 ,画出 △A2B2C2 .
图 11
(2)解不等式组 ,并把它的解集在数轴上表示出来. (6分)
(3)如图 12所示 , 四边形 ABCD 的对角线 AC,BD 交于点O. 若 O是 AC的中点 ,AE=CF,DF∥BE. (8 分)
①求证 :△BOE≌△DOF;
②若 OD= 则四边形 ABCD 是什么特殊四边形 请证明你的结论 .
图 12
3
(4)如图 13所示 ,x轴所在直线是一条东西走向的河 ,A( -2, 3) ,B(4, 5) 两个村庄位于河的北岸 , 现准 备在河上修建一净水站 P,并利用管道为两个村庄供水(单位:千米) . (8分)
①欲使所修管道最短 ,应该把净水站 P 修在什么位置 ,作出正确图形(用尺规作图) ,求出点 P 的坐标及 PB所在直线的解析式 ;
②若管道每米费用需要 200元 ,求修管道的最低费用 .
图 13
(5)如图 14所示 ,点 E,F分别在正方形 ABCD 的边 CD ,BC上 , ∠EAF= 45°. (8分)
①求证 :EF=DE+BF;
②作 AP⊥EF于点 P ,若 AD= 10,求 AP 的长 .
图 14
(6)甲 、乙两商场以同样的价格出售同样的商品 ,并且又各自推出不同的优惠方案 . 在甲商场累计购物 超过 100元后 ,超出 100元的部分按 90%收费 ;在乙商场累计购物超过 50元后 ,超出 50元的部分按 95%收 费 . 设小红在同一商场累计购物 x元 ,其中x>100. (12分)
①根据题意 ,填写下表(单位 :元) .
累计购物 130 290 … x
在甲商场实际花费 127 …
在乙商场实际花费 126 …
②当 x 取何值时 ,小红在甲 、乙两商场的实际花费相同
③当小红在同一商场累计购物超过 100元时 ,在哪家商场的实际花费少
4
同课章节目录
