2.2 立方根课件(共22张PPT)
文档属性
| 名称 | 2.2 立方根课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 457.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 12:05:30 | ||
图片预览







文档简介
(共22张PPT)
立方根
七年级下册 第二章 2.2
学习目标
1.理解立方根的定义,掌握符号表示,并能正确求非负数和负数的立方根。
2.区分立方根与平方根的异同,总结立方根的性质。
3.会用计算器求一个数的立方根或它的近似值。
复习回顾
已知一个正方体的体积为8cm3,如图所示,则它的棱长是多少?
解:∵23=8,
∴体积为8cm3的正方体的棱长是2cm.
这个问题的实质就是要找一个数, 使它的立方等于给定的数.
新知探究
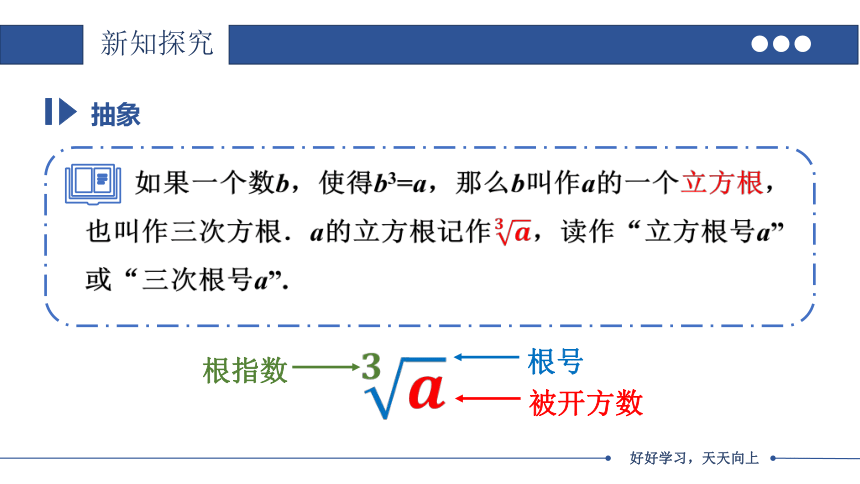
抽象
如果一个数b,使得b3=a,那么b叫作a的一个立方根,也叫作三次方根.a的立方根记作,读作“立方根号a”或“三次根号a”.
被开方数
根号
根指数
新知探究
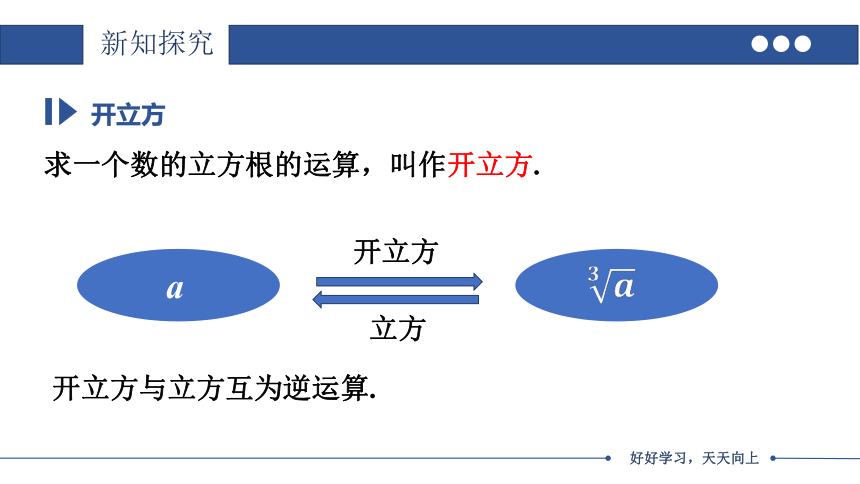
开立方
求一个数的立方根的运算,叫作开立方.
a
开立方
立方
开立方与立方互为逆运算.
新知探究
常见的立方数
13=1 23=8 33=27 43=64 53=125
63=216 73=343 83=512 93=729 103=1000
例题探究
例1分别求下列各数的立方根:
(1) 1; (2) ; (3) 0; (4) -0. 064.
解:(1) ∵13=1,∴=1.
(2) ∵3=,∴= .
(3) ∵03=0,∴=0.
(4) ∵(-0. 4)3=-0. 064 ,∴=-0. 4.
例题探究
1.每一个数有且只有一个立方根.
2.一个正数有一个正的立方根.
3.一个负数有一个负的立方根.
4. 0的立方根是0.
例题探究
判断题:
(1) 1的立方根是±1. ( )
(2) 立方根等于本身的数是0和1. ( )
(3) 一个数互为相反数,其立方根也互为相反数. ( )
(4) 0的平方根和立方根都是0. ( )
╳
√
√
╳
牛刀小试
例题探究
1.立方根等于本身的数是0和±1.
2.一个数互为相反数,其立方根也互为相反数.
3. 0的平方根和立方根都是0.
例2 用计算器求下列各数的立方根:(1) 343; (2) -1. 331.
例题探究
解:(1) 依次按键:
显示:7
所以=7
3
3
4
=
SHIFT
3
1
SHIFT
(-)
1
3
=
.
(2) 依次按键:
显示:-1.1
所以=-1.1
例3 用计算器求的近似值(结果精确到0. 001).
例题探究
实际上,许多有理数的立方根都是无理数,如,,…都是无理数,但可以用有理数来近似地表示它们.
解:依次按键:
显示结果:1.259 921 050.
所以1.260.
2
=
SHIFT
新知探究
议一议
下列等式是否成立?与同学交流你的看法.
(1); (2); (3).
解: (1)若x3=a,则x=,所以
(2)a的立方为a3,则a3的立方根是a,即.
(3)若b3=-a,则b=.若(-b)3=a,则-b=, b=,所以.
1. 64的立方根是 ( )
4
B. -4
C. ±4
D. 8
课堂练习
A
2.若一个数的立方根为 ,则这个数为( )
A.
B.
C.
D.
课堂练习
B
3.下列说法正确的是 ( )
A. 一个数的立方根有两个,它们互为相反数
B. 一个数的立方根比这个数的平方根小
C. 如果一个数有立方根,那么它一定有平方根
D. 与互为相反数
课堂练习
D
4.下列说法正确的是 ( )
A.8的立方根是±2
B.-64没有立方根
C.-1的立方根等于-1的立方
D.立方根等于本身的数只有0
课堂练习
C
5.若+=0,则x与y的关系一定是 ( )
A. x-y=0
B. xy=0
C. x+y=0
D. xy=-1
课堂练习
C
6.已知y的立方根是2,2x-y是16的算术平方根,求:
(1)x,y的值; (2)x2+y2的平方根.
课堂练习
解:(1)因为y的立方根是2,所以y=23=8.
因为2x-y是16的算术平方根,所以2x-y==4,所以x=6.
(2)因为x=6,y=8,所以x2+y2=62+82=100,
所以x2+y2的平方根为±=±10.
课堂小结
1.每一个数有且只有一个立方根.
2.一个正数有一个正的立方根.
3.一个负数有一个负的立方根.
4. 0的平方根和立方根都是0.
5.立方根等于本身的数是0和±1.
6.一个数互为相反数,其立方根也互为相反数.
课后作业
课堂作业:P37 T1
家庭作业:《学法》P28 A组(必做)
B、C组(选做)
立方根
七年级下册 第二章 2.2
学习目标
1.理解立方根的定义,掌握符号表示,并能正确求非负数和负数的立方根。
2.区分立方根与平方根的异同,总结立方根的性质。
3.会用计算器求一个数的立方根或它的近似值。
复习回顾
已知一个正方体的体积为8cm3,如图所示,则它的棱长是多少?
解:∵23=8,
∴体积为8cm3的正方体的棱长是2cm.
这个问题的实质就是要找一个数, 使它的立方等于给定的数.
新知探究
抽象
如果一个数b,使得b3=a,那么b叫作a的一个立方根,也叫作三次方根.a的立方根记作,读作“立方根号a”或“三次根号a”.
被开方数
根号
根指数
新知探究
开立方
求一个数的立方根的运算,叫作开立方.
a
开立方
立方
开立方与立方互为逆运算.
新知探究
常见的立方数
13=1 23=8 33=27 43=64 53=125
63=216 73=343 83=512 93=729 103=1000
例题探究
例1分别求下列各数的立方根:
(1) 1; (2) ; (3) 0; (4) -0. 064.
解:(1) ∵13=1,∴=1.
(2) ∵3=,∴= .
(3) ∵03=0,∴=0.
(4) ∵(-0. 4)3=-0. 064 ,∴=-0. 4.
例题探究
1.每一个数有且只有一个立方根.
2.一个正数有一个正的立方根.
3.一个负数有一个负的立方根.
4. 0的立方根是0.
例题探究
判断题:
(1) 1的立方根是±1. ( )
(2) 立方根等于本身的数是0和1. ( )
(3) 一个数互为相反数,其立方根也互为相反数. ( )
(4) 0的平方根和立方根都是0. ( )
╳
√
√
╳
牛刀小试
例题探究
1.立方根等于本身的数是0和±1.
2.一个数互为相反数,其立方根也互为相反数.
3. 0的平方根和立方根都是0.
例2 用计算器求下列各数的立方根:(1) 343; (2) -1. 331.
例题探究
解:(1) 依次按键:
显示:7
所以=7
3
3
4
=
SHIFT
3
1
SHIFT
(-)
1
3
=
.
(2) 依次按键:
显示:-1.1
所以=-1.1
例3 用计算器求的近似值(结果精确到0. 001).
例题探究
实际上,许多有理数的立方根都是无理数,如,,…都是无理数,但可以用有理数来近似地表示它们.
解:依次按键:
显示结果:1.259 921 050.
所以1.260.
2
=
SHIFT
新知探究
议一议
下列等式是否成立?与同学交流你的看法.
(1); (2); (3).
解: (1)若x3=a,则x=,所以
(2)a的立方为a3,则a3的立方根是a,即.
(3)若b3=-a,则b=.若(-b)3=a,则-b=, b=,所以.
1. 64的立方根是 ( )
4
B. -4
C. ±4
D. 8
课堂练习
A
2.若一个数的立方根为 ,则这个数为( )
A.
B.
C.
D.
课堂练习
B
3.下列说法正确的是 ( )
A. 一个数的立方根有两个,它们互为相反数
B. 一个数的立方根比这个数的平方根小
C. 如果一个数有立方根,那么它一定有平方根
D. 与互为相反数
课堂练习
D
4.下列说法正确的是 ( )
A.8的立方根是±2
B.-64没有立方根
C.-1的立方根等于-1的立方
D.立方根等于本身的数只有0
课堂练习
C
5.若+=0,则x与y的关系一定是 ( )
A. x-y=0
B. xy=0
C. x+y=0
D. xy=-1
课堂练习
C
6.已知y的立方根是2,2x-y是16的算术平方根,求:
(1)x,y的值; (2)x2+y2的平方根.
课堂练习
解:(1)因为y的立方根是2,所以y=23=8.
因为2x-y是16的算术平方根,所以2x-y==4,所以x=6.
(2)因为x=6,y=8,所以x2+y2=62+82=100,
所以x2+y2的平方根为±=±10.
课堂小结
1.每一个数有且只有一个立方根.
2.一个正数有一个正的立方根.
3.一个负数有一个负的立方根.
4. 0的平方根和立方根都是0.
5.立方根等于本身的数是0和±1.
6.一个数互为相反数,其立方根也互为相反数.
课后作业
课堂作业:P37 T1
家庭作业:《学法》P28 A组(必做)
B、C组(选做)
同课章节目录
