2024-2025学年九年级下学期数学(人教版)期中考试(含解析)
文档属性
| 名称 | 2024-2025学年九年级下学期数学(人教版)期中考试(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 753.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级2024-2025学年九年级下册期中考试(人教版)
数学
考试范围:第二十六章-第二十七章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题3分,共30分,在每小题给出的四个选项中,只有一个符合题目要求)
1.有理数、在数轴上的位置如图所示,则数,,,的大小关系为( )
A. B.
C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面的总面积约为250000m2,将数据250000用科学记数法可表示为( )
A. B. C.2.5×104 D.0.25×106
4.如图是由六个相同的小正方体搭成的几何体,这个几何体的左视图是( )
A. B.
C. D.
5.下列说法错误的是( )
A.数据的中位数是.
B.为了解昆明市中学生对“古滇文化”的知晓情况,适宜采用抽样调查.
C.若甲、乙两组数据的方差 ,则乙组数据比甲组数据稳定.
D.为了解名学生体质达标情况,从中抽测了名学生,样本是名学生.
6.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
7.如图,菱形,点均在坐标轴上,,点,点是的中点,点是上的一动点,则的最小值是( )
A.3 B.5 C. D.
8.在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50.如果乙得到甲所有钱的,那么乙也共有钱50.甲、乙两人各需带多少钱?设甲需带钱x,乙需带钱y,根据题意可列方程组为( )
A. B.
C. D.
9.如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=mx+n与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN的值最小,则点P的坐标为( )
A.(0,2) B.(0,) C.(0,) D.(0,)
10.如图,在边长为的正方形中,是边上一动点不含,两点,将沿直线翻折,点落在点处;在上有一点,使得将沿直线翻折后,点落在直线上的点处,直线交于点,连接,则以下结论中正确的是( )
线段长度的最小值为;
四边形的面积最大值为;
当≌时,;
当为中点时,是线段的垂直平分线.
A. B. C. D.
二、填空题(本题共5小题,每小题4分,共20分)
11.计算: .
12.已知,若有一角与的两边分别平行,则该角的度数为 ,另有,若的一边,另一边与直线相交于点P,且点E不在直线上,则的度数为 .
13.已知关于的一元二次方程有解,求的取值范围 .
14.在矩形中,以D为圆心,为半径画弧,交于点E,再以为直径作半圆交弧于点F,连接、,若,则图中阴影部分的面积为 .
15.已知,矩形中,,,为边上一动点,以为边构造等边(点位于下方),连接.
⑴如图①,当时, ;
⑵点在运动的过程中,的最小值为 .
三、解答题(本题共7小题,共70分)
16.先化简,再求值:其中的值从不等式组的整数解中选取.
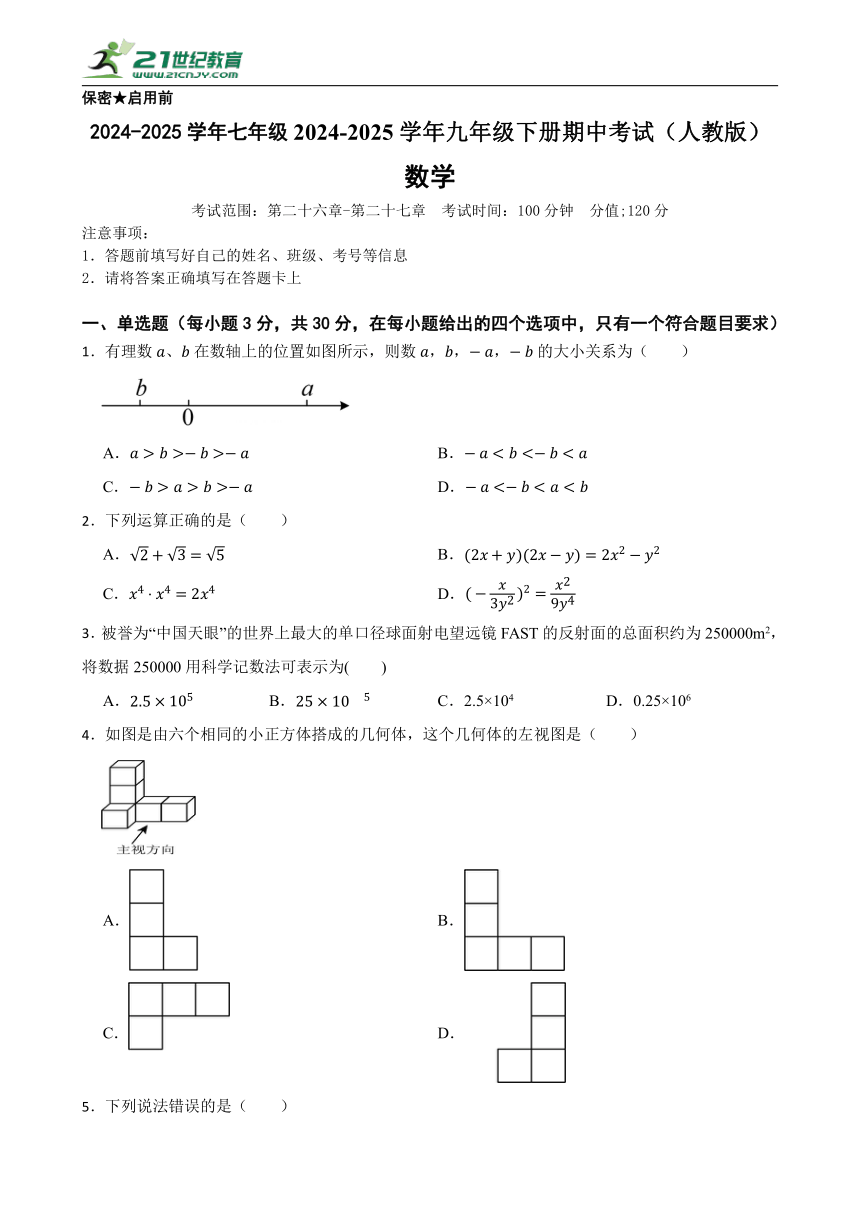
17.春季开学后,某校为了让学生有效应用压岁钱,开展有意义的“尊老、敬老”慈善捐款活动,将捐款捐赠给本市敬老院.学生会为了了解学生捐款的情况,随机调查了该校部分学生,根据调查结果,绘制了两幅不完整的统计图.请根据相关信息,解答下列问题:
(1)本次调查的学生人数为 人,在扇形统计图中,捐款金额为100元所在扇形的圆心角的度数是 度,在调查的这组学生中,捐款金额的中位数是 元;
(2)补全条形统计图;
(3)学生会为了更好地引导学生合理支配压岁钱,选出甲,乙,丙和丁四人从不同的方面在全校进行讲解,但由于时间的限定,临时调整只能两人讲解.因此,学生会采用随机抽签的方式从甲,乙,丙和丁四人中确定两名讲解人选.请用列表或画树状图的方式说明抽中甲和乙的概率是多少?
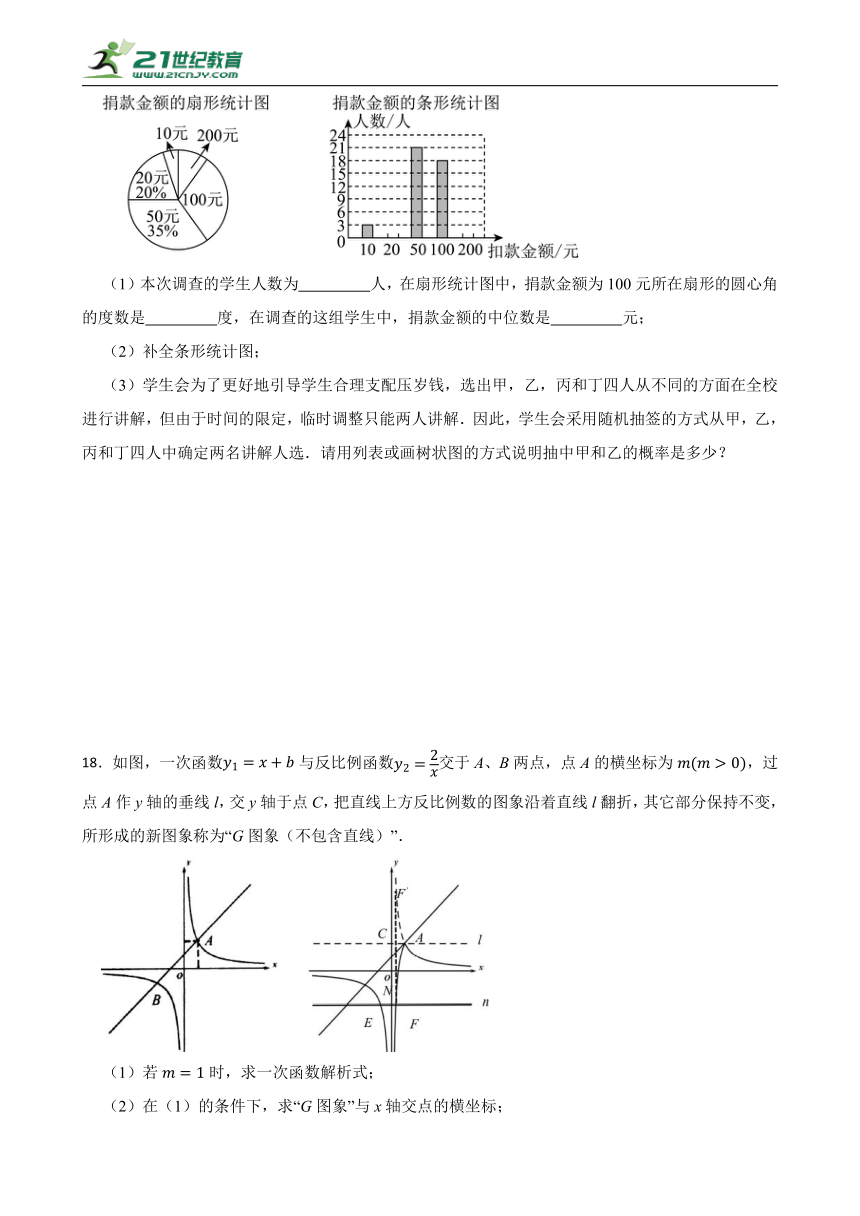
18.如图,一次函数与反比例函数交于A、B两点,点A的横坐标为,过点A作y轴的垂线l,交y轴于点C,把直线上方反比例数的图象沿着直线l翻折,其它部分保持不变,所形成的新图象称为“G图象(不包含直线)”.
(1)若时,求一次函数解析式;
(2)在(1)的条件下,求“G图象”与x轴交点的横坐标;
(3)过y轴另一点作y轴的垂线,与“G图象”交于E,F两点
①若时,且,求m的值;
②若,直接写出n与m的数量关系(用含m的代数式表示n)
19.如图1,CD是的弦,半径,垂足为B,过点C作的切线l.
(1)若点E在上,且,连接OE.
①连接AE,求证:;
②如图2,若B是OA的中点,连接OD,求证:DE是的直径;
(2)如图3,过点B作,垂足为F,若的半径是4,求的最大值.
20.为方便山区的山货运输,某地计划在图1所示的山上开辟一条山路,其截面示意图如图2.从山脚的点开始向山上修建坡道和,并在点与点之间设置一段与地面平行的平路,其中,,坡道,的坡角分别为,.
(1)求点到水平地面的高度;
(2)求点与点之间的水平距离.
(结果精确到1.参考数据:,,,)
21.我们把纵坐标是横坐标两倍的点叫双语点,如点,点.
(1)函数的双语点是 ;
(2)函数(k为常数,目)上是否存在双语点?若存在,求出双语点的坐标,若不存在,请说明理由;
(3)函数的图象上只有唯一一个双语点,且当时,m的最小值为k,求实数k的值.
22.如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t秒(0<t≤4).
(1)写出△PBQ的面积S(cm2)与时间t(s)的函数关系式,当t为何值时,S有最大值,最大值是多少?
(2)当t为何值时,△PBQ为等腰三角形?
23.如图1,一块矩形电子屏ABCD中,G为BC上一感应点,GC=2,动点P为一光点,当光点在光带上运动时,会与感应点发生反应,照亮以GP为边的正方形区域GPEF.因发生故障,只有光带CM和MB正常工作,CM=4,光点P以每秒1个单位的速度从C点出发,沿C→M→B匀速运动,到达点B时停止.设光点P的运动时间为t秒,照亮的正方形区域GPEF的面积为S.图2为P点在运动过程中S与t的函数图象,其中点Q表示P点运动到B点时情形.
(1)图2中a= ;当t=1时,照亮的区域面积S= .
(2)当点P经过M点又运动4秒时,照亮区域的面积达到了最小,已知此时S是t的二次函数.求出点P在整个运动过程中S关于t的函数解析式;
(3)若存在三个时刻t1、t2、t3(t1<t2<t3)对应的正方形的面积均相等.①t1+t2= ;②当t3=4t1时,则正方形GPEF的面积为 .
答案解析部分
1.B
解:由题意可知:
a>0>b,,
∴-a<0<-b,a>-b,-a<b
-a<b<0<-b<a
B正确.
故答案为:B.
本题考查了利用数轴比大小,数轴右边的点所表示的数值永远大于左边的点所表示的数值;离原点越远的点的绝对值越大,互为相反数的点的到原点的距离相等,即绝对值相等,据此可判断得出答案.
2.D
A、∵不是同类二次根式,∴A不符合题意;
B、∵,∴B不符合题意;
C、∵,∴C不符合题意;
D、∵,∴D符合题意;
故答案为:D.
利用二次根式的加法、平方差公式、同底数幂的乘法及幂的乘方逐项判断即可。
3.A
解:
故答案为:A .
用科学记数法表示一个绝对值大于1的数,把它写成的形式,其中,n为整数.小数点移动几位到第一位数字后面,n就等于几,n也可以说是原数整数部分位数减1.
4.A
解:从左面看,底层是2个小正方形,第二层是1个小正方形,第三层是1个小正方形,
∴几何体的左视图是:
,
故答案为:A.
根据从左面看到的图形判定即可.
5.D
解:、数据按照由小到大的顺序排列为,
∴数据的中位数为,该选项正确,不合题意;
、为了解昆明市中学生对“古滇文化”的知晓情况,适宜采用抽样调查,该选项正确,不合题意;
、若甲、乙两组数据的方差,则乙组数据比甲组数据稳定,该选项正确,不合题意;
、为了解名学生体质达标情况,从中抽测了名学生,样本是名学生的体质情况,该选项错误,符合题意;
故答案为:
根据中位数的定义、抽样调查、方差的定义、样本的定义对选项逐一判断即可求解。
6.A
解:解不等式3x-9<0,得x<3;
解不等式4x+6≤22,得x≤4,
∴不等式组的解集为x<3.
故答案为:A.
首先分别求出两个不等式的解集,取其公共部分即为不等式组的解集,然后根据解集的表示方法进行判断.
7.A
8.D
9.A
解:如图,作点N关于y轴的对称点N',连结MN'交y轴于点P,此时PM+PN的值最小.
将点N的坐标代人抛物线表达式,并联立对称轴公式,得
,解得
∴y=-x2-6x-4=-(x+3)2+5,
∴M(-3,5).
点N关于y轴的对称点为点N'(1,1),
设直线MN'的表达式为y=kx+b(k≠0),
将点M,N'的坐标代人直线表达式,得,解得
∴直线MN'的表达式为y=-x+2,
当x=0时,y=2,即P(0,2).
故答案为:A.
作点N关于y轴的对称点N',连结MN'交y轴于点P,此时PM+PN的值最小,由待定系数法求出二次函数的解析式y=-(x+3)2+5,得到点M的坐标,由对称性得点N关于y轴的对称点为点
N'(1,1),然后用待定系数法求出直线MN'的表达式为y=-x+2,令x=0,即可得P点坐标.
10.A
解:四边形为正方形,边长为,
,,
设,则,
由折叠知:,,
点、、三点在通一条直线上,
,即:,
,
又,
,
又,
∽,
,
,
,
在中,由勾股定理得:,
当为最小时,为最小,
,
当时,DM为最小,最小值为,
即当DM=3时,为最小,
此时,
故结论正确;
设四边形的面积为,
则,
由可知:,,
,
当时,为最大,最大值为,
四边形的面积最大值为.
故结论正确;
由翻折的性质可知:≌,
,,
在和中,
,,
≌,
又≌,
≌≌≌,
,
在上取一点,使,
,
,
为等腰直角三角形,
,
由勾股定理得:,
,
,
即:,
解得:,
,
故结论正确;
点为的中点,
,
设,
由可知:≌,
,
,,
在中,由勾股定理得:,
即:,
解得:,
即:,
,
不是线段的垂直平分线,
故结论不正确.
综上所述:正确的结论是.
故选:.
根据正方形的性质,相似三角形的判定与性质,勾股定理,折叠性质,一元二次方程根的判别式,二次函数的最值即可求出答案。
11.20
12.或;,,,
13.且
解:∵一元二次方程有解,
∴k-1≠0,△=k-4(k-1)20,
解不等式得:k,且k≠1,
∵有意义,
∴k0,
综上所述:且,
故答案为:且
根据方程有解可知△=k-4(k-1)20,再根据 有意义可知k0,据此求出公共解集即可.
14.
15.45;
解:如图所示,连接交于O,连接,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∴是等边三角形,
∴,
∴
∵是等边三角形,
∴,
∴,
∴ ,
∴,
∴;
当时,则,,
∴,,
又∵,
∴,
∴,
∴;
∵,
∴点F在直线上运动(直线与的夹角为30度),
∴当时,有最小值,
∴此时,
故答案为:45;.
(1)连接AC、BD交于O,连接OF、AE,由矩形的性质和勾股定理求出AC的长,进而得到,证明是等边三角形,得到, 则,再根据SAS证明 ,得到,则;当时,则,,可求出,则,由此可得;
(2)由确定点F在直线上运动(直线与的夹角为30度),故当时,有最小值,则此时.
16.,-2
17.(1)60;108;50
(2)解:补全条形统计图如图.
(3)解:画树状图得:
解:(1)由扇形图和条形图可知: 捐款50元的频数和百分数分别为21人、35%,∴本次调查的学生人数为21÷35%=60(人);由扇形图和条形图可知:捐款100元的频数为18人,∴捐款金额为100元所在扇形的圆心角的度数=×360°=108°;捐款20元的频数=60×20%=12(人),∴捐款金额的中位数=(人);
(2)由(1)得:捐款20元的频数=12(人);捐款200元的频数=60-3-12-21-18=6(人),在条形图中补充完整;
(3)由树状图可知:所有可能的结果为12种,抽中甲和乙的机会有2次,∴抽中甲和乙的概率=.
(1)由扇形图和条形图可知: 捐款50元的频数和百分数分别为21人、35%,根据样本容量=频数÷百分数可求得本次调查的学生人数;捐款金额为100元所在扇形的圆心角的度数=捐款金额为100元的百分数×360°;中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数,根据定义和已知可求得捐款金额的中位数;
(2)根据样本容量等于各小组频数之和可求得捐款200元的频数,结合(1)的计算可将条形图中补充完整;
(3)由题意画出树状图,观察树状图可知:所有可能的结果为12种,抽中甲和乙的机会有2次,然后用概率公式计算即可求解.
18.(1)解:当时,,即
一次函数经过
所以一次函数
(2)解:设“G图象”与x轴交点的坐标为
关于的对称点的坐标为,
根据题意,在上,,
即“图象G”与x轴交点的横坐标为.
(3)解:①
∴令,则,即
即
当时,,即
②
解:②当时,
,
解得:,
,
,
,
,
,
,
当时,
,
在反比例函数上,
点A的横坐标为,
直线l为,
点与关于直线l为对称,
,
解得:,
故n与m的数量关系为.
本题考查一次函数与反比例函数综合,待定系数法求函数的解析式,对称的性质.
(1)将代入,求出,将点A代入可求出b,进而求出答案;
(2)设“G图象”与x轴交点为,可得直线l为,由对称得关于直线的对称点的坐标为,将此点代入,可求出与x轴交点的横坐标 ;
(3)①将代入,可求出,从而求出, 在反比例函数上,由点与关于直线l为对称,可得,解方程可求出m的值;
②将代入,可求出,进而求出,,由点与关于直线l为对称可得方程,化简式子可求出答案.
19.(1)解:证明:①如图4,连接OC
∵ l是的切线,OC是半径,
∴
∵
∴
∵
∴
∴;
②:如图5,连接OC,AD
∵ B是OA的中点,
∴,
又∵
∴
∴是等边三角形
∴
∵
∴
∴
∴DE是的直径;
(2)解:如图6,连接OC
∵ l是的切线,OC是半径,
∴
∵
∴
∴
∵
∴
∴
设,则
∴
当时,有最大值1
∴的最大值为1.
(1)①连接OC,根据切线的性质可得OC⊥l,根据弧、圆心角的关系可得∠COE=∠COA,由等腰三角形的性质可得OC⊥AE,然后根据垂直于同一直线的两直线互相平行进行证明;
②由题意可得OD=AD=AD,推出△OAD为等边三角形,得到∠DOA=60°,由弧、圆心角的关系可得∠DOA=∠AOC=∠EOC=60°,则∠DOE=180°,据此证明;
(2)连接OC,易得OC∥BF,由平行线的性质可得∠OCB=∠CBF,证明△OCB∽△CBF,根据相似三角形的性质表示出BF,然后表示出BC-BF,接下来利用二次函数的性质进行解答.
20.(1)点到水平地面的高度是150米.
(2)点与点之间的水平距离1049米.
21.(1)(-1,-2)
(2)解:不存在双语点,理由如下,
依题意,
即,
∴,
当时,解得:或
当时,无解
∴和;
∴当时,有两个双语点,分别为和;
当时,不存在双语点;
(3)解:依题意,
整理得,,
∵函数的图象上只有唯一一个双语点,
∴有相等的两个实数根,
∴
∴
∴
对称轴为直线,开口向上,
当,时,,
即时,解得:,
当时,则当时,取得最小值
∵m的最小值为k
∴
即,
∵
∴原方程无解,
当时,则当时,取得小值,
∴
即
解得:或(舍去)
综上所述:或.
解:(1)解:依题意,
解得:
∴函数的双语点是:(-1,-2);
故答案为:(-1,-2);
(1)根据题意可得方程组,解方程组,即可求出答案;
(2)根据题意可得方程组 ,由此得 , 然后分当k>0 与k<0 两种情况解答即可;
(3)易得 ,整理得 ,根据函数图象上只有唯一一个双语点,可得该方程根的判别式的值为0,据此建立出m关于n函数解析式,根据函数最值情况即可解决问题.
22.(1)解:矩形中,,
过点P作,垂足为M,
,
,
,
当时,S有最大值;
(2)解:①当时,,
,
②当时,作,垂足为E,
此时,,
即,
.
③当时,作,垂足为F,
此时,,
即,
.
或或均使为等腰三角形.
(1)首先根据勾股定理求出BD,过点P作PM⊥BC,垂足为M,则△BPM∽△BDC,根据相似三角形的性质可得PM,利用三角形的面积公式表示出S,然后根据二次函数的性质可得S的最大值;
(2)①当BP=BQ时,可得t的值;②当BQ=PQ时,作QE⊥BD,垂足为E,此时BE= ,易证△BQE∽△BDC,然后根据相似三角形的性质可得t的值;③当BP=PQ时,作PF⊥BC,垂足为F,此时BF= ,易证△BPF∽△BDC,然后根据相似三角形的性质可得t的值.
23.(1)24;9
(2)解:i)当 时,
ii)当 时, 由已知可得抛物线的顶点为
设解析式为 ,
图象经过
抛物线的解析式为:
综上所述, 点 在整个运动过程中 关于 的函数解析式为
(3)8;
解:(1)由题意,当t=4时,PC=4,由勾股定理得GP2=GC2+PC2=(2)2+42=24,S=GP2=24,故a=24.当t=1时,PC=1,GP2=GC2+PC2=(2)2+12=9,故S=9;
(3)如图所示,
当0≤t≤8时,图像关于直线x=4对称,且存在 三个时刻t1、t2、t3(t1<t2<t3)对应的正方形的面积均相等,故 t1+t2= 8;
当t>4时,,图像关于直线x=8对称,故t2+t3=16,
同时 t1+t2= 8, t3=4t1 ,
解得t3=,
代入函数解析式得S=
(1)由图像当t=4时,S=a,求出此时的PC的长得GP的平方,即为正方形的面积,同理当t=1时,求出GP2,即为面积;
(2)当t<4时,求出GP2的表达式,即为面积表达式;当t>4时,结合题意设顶点式,代入(4,24)即可求出解析式;
(3)结合图像的对称性知 t1+t2= 8,t2+t3=16,同时 t3=4t1,求出t3的值,代入函数解析式即可得对应的面积.
2024-2025学年七年级2024-2025学年九年级下册期中考试(人教版)
数学
考试范围:第二十六章-第二十七章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题3分,共30分,在每小题给出的四个选项中,只有一个符合题目要求)
1.有理数、在数轴上的位置如图所示,则数,,,的大小关系为( )
A. B.
C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面的总面积约为250000m2,将数据250000用科学记数法可表示为( )
A. B. C.2.5×104 D.0.25×106
4.如图是由六个相同的小正方体搭成的几何体,这个几何体的左视图是( )
A. B.
C. D.
5.下列说法错误的是( )
A.数据的中位数是.
B.为了解昆明市中学生对“古滇文化”的知晓情况,适宜采用抽样调查.
C.若甲、乙两组数据的方差 ,则乙组数据比甲组数据稳定.
D.为了解名学生体质达标情况,从中抽测了名学生,样本是名学生.
6.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
7.如图,菱形,点均在坐标轴上,,点,点是的中点,点是上的一动点,则的最小值是( )
A.3 B.5 C. D.
8.在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50.如果乙得到甲所有钱的,那么乙也共有钱50.甲、乙两人各需带多少钱?设甲需带钱x,乙需带钱y,根据题意可列方程组为( )
A. B.
C. D.
9.如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=mx+n与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN的值最小,则点P的坐标为( )
A.(0,2) B.(0,) C.(0,) D.(0,)
10.如图,在边长为的正方形中,是边上一动点不含,两点,将沿直线翻折,点落在点处;在上有一点,使得将沿直线翻折后,点落在直线上的点处,直线交于点,连接,则以下结论中正确的是( )
线段长度的最小值为;
四边形的面积最大值为;
当≌时,;
当为中点时,是线段的垂直平分线.
A. B. C. D.
二、填空题(本题共5小题,每小题4分,共20分)
11.计算: .
12.已知,若有一角与的两边分别平行,则该角的度数为 ,另有,若的一边,另一边与直线相交于点P,且点E不在直线上,则的度数为 .
13.已知关于的一元二次方程有解,求的取值范围 .
14.在矩形中,以D为圆心,为半径画弧,交于点E,再以为直径作半圆交弧于点F,连接、,若,则图中阴影部分的面积为 .
15.已知,矩形中,,,为边上一动点,以为边构造等边(点位于下方),连接.
⑴如图①,当时, ;
⑵点在运动的过程中,的最小值为 .
三、解答题(本题共7小题,共70分)
16.先化简,再求值:其中的值从不等式组的整数解中选取.
17.春季开学后,某校为了让学生有效应用压岁钱,开展有意义的“尊老、敬老”慈善捐款活动,将捐款捐赠给本市敬老院.学生会为了了解学生捐款的情况,随机调查了该校部分学生,根据调查结果,绘制了两幅不完整的统计图.请根据相关信息,解答下列问题:
(1)本次调查的学生人数为 人,在扇形统计图中,捐款金额为100元所在扇形的圆心角的度数是 度,在调查的这组学生中,捐款金额的中位数是 元;
(2)补全条形统计图;
(3)学生会为了更好地引导学生合理支配压岁钱,选出甲,乙,丙和丁四人从不同的方面在全校进行讲解,但由于时间的限定,临时调整只能两人讲解.因此,学生会采用随机抽签的方式从甲,乙,丙和丁四人中确定两名讲解人选.请用列表或画树状图的方式说明抽中甲和乙的概率是多少?
18.如图,一次函数与反比例函数交于A、B两点,点A的横坐标为,过点A作y轴的垂线l,交y轴于点C,把直线上方反比例数的图象沿着直线l翻折,其它部分保持不变,所形成的新图象称为“G图象(不包含直线)”.
(1)若时,求一次函数解析式;
(2)在(1)的条件下,求“G图象”与x轴交点的横坐标;
(3)过y轴另一点作y轴的垂线,与“G图象”交于E,F两点
①若时,且,求m的值;
②若,直接写出n与m的数量关系(用含m的代数式表示n)
19.如图1,CD是的弦,半径,垂足为B,过点C作的切线l.
(1)若点E在上,且,连接OE.
①连接AE,求证:;
②如图2,若B是OA的中点,连接OD,求证:DE是的直径;
(2)如图3,过点B作,垂足为F,若的半径是4,求的最大值.
20.为方便山区的山货运输,某地计划在图1所示的山上开辟一条山路,其截面示意图如图2.从山脚的点开始向山上修建坡道和,并在点与点之间设置一段与地面平行的平路,其中,,坡道,的坡角分别为,.
(1)求点到水平地面的高度;
(2)求点与点之间的水平距离.
(结果精确到1.参考数据:,,,)
21.我们把纵坐标是横坐标两倍的点叫双语点,如点,点.
(1)函数的双语点是 ;
(2)函数(k为常数,目)上是否存在双语点?若存在,求出双语点的坐标,若不存在,请说明理由;
(3)函数的图象上只有唯一一个双语点,且当时,m的最小值为k,求实数k的值.
22.如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t秒(0<t≤4).
(1)写出△PBQ的面积S(cm2)与时间t(s)的函数关系式,当t为何值时,S有最大值,最大值是多少?
(2)当t为何值时,△PBQ为等腰三角形?
23.如图1,一块矩形电子屏ABCD中,G为BC上一感应点,GC=2,动点P为一光点,当光点在光带上运动时,会与感应点发生反应,照亮以GP为边的正方形区域GPEF.因发生故障,只有光带CM和MB正常工作,CM=4,光点P以每秒1个单位的速度从C点出发,沿C→M→B匀速运动,到达点B时停止.设光点P的运动时间为t秒,照亮的正方形区域GPEF的面积为S.图2为P点在运动过程中S与t的函数图象,其中点Q表示P点运动到B点时情形.
(1)图2中a= ;当t=1时,照亮的区域面积S= .
(2)当点P经过M点又运动4秒时,照亮区域的面积达到了最小,已知此时S是t的二次函数.求出点P在整个运动过程中S关于t的函数解析式;
(3)若存在三个时刻t1、t2、t3(t1<t2<t3)对应的正方形的面积均相等.①t1+t2= ;②当t3=4t1时,则正方形GPEF的面积为 .
答案解析部分
1.B
解:由题意可知:
a>0>b,,
∴-a<0<-b,a>-b,-a<b
-a<b<0<-b<a
B正确.
故答案为:B.
本题考查了利用数轴比大小,数轴右边的点所表示的数值永远大于左边的点所表示的数值;离原点越远的点的绝对值越大,互为相反数的点的到原点的距离相等,即绝对值相等,据此可判断得出答案.
2.D
A、∵不是同类二次根式,∴A不符合题意;
B、∵,∴B不符合题意;
C、∵,∴C不符合题意;
D、∵,∴D符合题意;
故答案为:D.
利用二次根式的加法、平方差公式、同底数幂的乘法及幂的乘方逐项判断即可。
3.A
解:
故答案为:A .
用科学记数法表示一个绝对值大于1的数,把它写成的形式,其中,n为整数.小数点移动几位到第一位数字后面,n就等于几,n也可以说是原数整数部分位数减1.
4.A
解:从左面看,底层是2个小正方形,第二层是1个小正方形,第三层是1个小正方形,
∴几何体的左视图是:
,
故答案为:A.
根据从左面看到的图形判定即可.
5.D
解:、数据按照由小到大的顺序排列为,
∴数据的中位数为,该选项正确,不合题意;
、为了解昆明市中学生对“古滇文化”的知晓情况,适宜采用抽样调查,该选项正确,不合题意;
、若甲、乙两组数据的方差,则乙组数据比甲组数据稳定,该选项正确,不合题意;
、为了解名学生体质达标情况,从中抽测了名学生,样本是名学生的体质情况,该选项错误,符合题意;
故答案为:
根据中位数的定义、抽样调查、方差的定义、样本的定义对选项逐一判断即可求解。
6.A
解:解不等式3x-9<0,得x<3;
解不等式4x+6≤22,得x≤4,
∴不等式组的解集为x<3.
故答案为:A.
首先分别求出两个不等式的解集,取其公共部分即为不等式组的解集,然后根据解集的表示方法进行判断.
7.A
8.D
9.A
解:如图,作点N关于y轴的对称点N',连结MN'交y轴于点P,此时PM+PN的值最小.
将点N的坐标代人抛物线表达式,并联立对称轴公式,得
,解得
∴y=-x2-6x-4=-(x+3)2+5,
∴M(-3,5).
点N关于y轴的对称点为点N'(1,1),
设直线MN'的表达式为y=kx+b(k≠0),
将点M,N'的坐标代人直线表达式,得,解得
∴直线MN'的表达式为y=-x+2,
当x=0时,y=2,即P(0,2).
故答案为:A.
作点N关于y轴的对称点N',连结MN'交y轴于点P,此时PM+PN的值最小,由待定系数法求出二次函数的解析式y=-(x+3)2+5,得到点M的坐标,由对称性得点N关于y轴的对称点为点
N'(1,1),然后用待定系数法求出直线MN'的表达式为y=-x+2,令x=0,即可得P点坐标.
10.A
解:四边形为正方形,边长为,
,,
设,则,
由折叠知:,,
点、、三点在通一条直线上,
,即:,
,
又,
,
又,
∽,
,
,
,
在中,由勾股定理得:,
当为最小时,为最小,
,
当时,DM为最小,最小值为,
即当DM=3时,为最小,
此时,
故结论正确;
设四边形的面积为,
则,
由可知:,,
,
当时,为最大,最大值为,
四边形的面积最大值为.
故结论正确;
由翻折的性质可知:≌,
,,
在和中,
,,
≌,
又≌,
≌≌≌,
,
在上取一点,使,
,
,
为等腰直角三角形,
,
由勾股定理得:,
,
,
即:,
解得:,
,
故结论正确;
点为的中点,
,
设,
由可知:≌,
,
,,
在中,由勾股定理得:,
即:,
解得:,
即:,
,
不是线段的垂直平分线,
故结论不正确.
综上所述:正确的结论是.
故选:.
根据正方形的性质,相似三角形的判定与性质,勾股定理,折叠性质,一元二次方程根的判别式,二次函数的最值即可求出答案。
11.20
12.或;,,,
13.且
解:∵一元二次方程有解,
∴k-1≠0,△=k-4(k-1)20,
解不等式得:k,且k≠1,
∵有意义,
∴k0,
综上所述:且,
故答案为:且
根据方程有解可知△=k-4(k-1)20,再根据 有意义可知k0,据此求出公共解集即可.
14.
15.45;
解:如图所示,连接交于O,连接,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∴是等边三角形,
∴,
∴
∵是等边三角形,
∴,
∴,
∴ ,
∴,
∴;
当时,则,,
∴,,
又∵,
∴,
∴,
∴;
∵,
∴点F在直线上运动(直线与的夹角为30度),
∴当时,有最小值,
∴此时,
故答案为:45;.
(1)连接AC、BD交于O,连接OF、AE,由矩形的性质和勾股定理求出AC的长,进而得到,证明是等边三角形,得到, 则,再根据SAS证明 ,得到,则;当时,则,,可求出,则,由此可得;
(2)由确定点F在直线上运动(直线与的夹角为30度),故当时,有最小值,则此时.
16.,-2
17.(1)60;108;50
(2)解:补全条形统计图如图.
(3)解:画树状图得:
解:(1)由扇形图和条形图可知: 捐款50元的频数和百分数分别为21人、35%,∴本次调查的学生人数为21÷35%=60(人);由扇形图和条形图可知:捐款100元的频数为18人,∴捐款金额为100元所在扇形的圆心角的度数=×360°=108°;捐款20元的频数=60×20%=12(人),∴捐款金额的中位数=(人);
(2)由(1)得:捐款20元的频数=12(人);捐款200元的频数=60-3-12-21-18=6(人),在条形图中补充完整;
(3)由树状图可知:所有可能的结果为12种,抽中甲和乙的机会有2次,∴抽中甲和乙的概率=.
(1)由扇形图和条形图可知: 捐款50元的频数和百分数分别为21人、35%,根据样本容量=频数÷百分数可求得本次调查的学生人数;捐款金额为100元所在扇形的圆心角的度数=捐款金额为100元的百分数×360°;中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数,根据定义和已知可求得捐款金额的中位数;
(2)根据样本容量等于各小组频数之和可求得捐款200元的频数,结合(1)的计算可将条形图中补充完整;
(3)由题意画出树状图,观察树状图可知:所有可能的结果为12种,抽中甲和乙的机会有2次,然后用概率公式计算即可求解.
18.(1)解:当时,,即
一次函数经过
所以一次函数
(2)解:设“G图象”与x轴交点的坐标为
关于的对称点的坐标为,
根据题意,在上,,
即“图象G”与x轴交点的横坐标为.
(3)解:①
∴令,则,即
即
当时,,即
②
解:②当时,
,
解得:,
,
,
,
,
,
,
当时,
,
在反比例函数上,
点A的横坐标为,
直线l为,
点与关于直线l为对称,
,
解得:,
故n与m的数量关系为.
本题考查一次函数与反比例函数综合,待定系数法求函数的解析式,对称的性质.
(1)将代入,求出,将点A代入可求出b,进而求出答案;
(2)设“G图象”与x轴交点为,可得直线l为,由对称得关于直线的对称点的坐标为,将此点代入,可求出与x轴交点的横坐标 ;
(3)①将代入,可求出,从而求出, 在反比例函数上,由点与关于直线l为对称,可得,解方程可求出m的值;
②将代入,可求出,进而求出,,由点与关于直线l为对称可得方程,化简式子可求出答案.
19.(1)解:证明:①如图4,连接OC
∵ l是的切线,OC是半径,
∴
∵
∴
∵
∴
∴;
②:如图5,连接OC,AD
∵ B是OA的中点,
∴,
又∵
∴
∴是等边三角形
∴
∵
∴
∴
∴DE是的直径;
(2)解:如图6,连接OC
∵ l是的切线,OC是半径,
∴
∵
∴
∴
∵
∴
∴
设,则
∴
当时,有最大值1
∴的最大值为1.
(1)①连接OC,根据切线的性质可得OC⊥l,根据弧、圆心角的关系可得∠COE=∠COA,由等腰三角形的性质可得OC⊥AE,然后根据垂直于同一直线的两直线互相平行进行证明;
②由题意可得OD=AD=AD,推出△OAD为等边三角形,得到∠DOA=60°,由弧、圆心角的关系可得∠DOA=∠AOC=∠EOC=60°,则∠DOE=180°,据此证明;
(2)连接OC,易得OC∥BF,由平行线的性质可得∠OCB=∠CBF,证明△OCB∽△CBF,根据相似三角形的性质表示出BF,然后表示出BC-BF,接下来利用二次函数的性质进行解答.
20.(1)点到水平地面的高度是150米.
(2)点与点之间的水平距离1049米.
21.(1)(-1,-2)
(2)解:不存在双语点,理由如下,
依题意,
即,
∴,
当时,解得:或
当时,无解
∴和;
∴当时,有两个双语点,分别为和;
当时,不存在双语点;
(3)解:依题意,
整理得,,
∵函数的图象上只有唯一一个双语点,
∴有相等的两个实数根,
∴
∴
∴
对称轴为直线,开口向上,
当,时,,
即时,解得:,
当时,则当时,取得最小值
∵m的最小值为k
∴
即,
∵
∴原方程无解,
当时,则当时,取得小值,
∴
即
解得:或(舍去)
综上所述:或.
解:(1)解:依题意,
解得:
∴函数的双语点是:(-1,-2);
故答案为:(-1,-2);
(1)根据题意可得方程组,解方程组,即可求出答案;
(2)根据题意可得方程组 ,由此得 , 然后分当k>0 与k<0 两种情况解答即可;
(3)易得 ,整理得 ,根据函数图象上只有唯一一个双语点,可得该方程根的判别式的值为0,据此建立出m关于n函数解析式,根据函数最值情况即可解决问题.
22.(1)解:矩形中,,
过点P作,垂足为M,
,
,
,
当时,S有最大值;
(2)解:①当时,,
,
②当时,作,垂足为E,
此时,,
即,
.
③当时,作,垂足为F,
此时,,
即,
.
或或均使为等腰三角形.
(1)首先根据勾股定理求出BD,过点P作PM⊥BC,垂足为M,则△BPM∽△BDC,根据相似三角形的性质可得PM,利用三角形的面积公式表示出S,然后根据二次函数的性质可得S的最大值;
(2)①当BP=BQ时,可得t的值;②当BQ=PQ时,作QE⊥BD,垂足为E,此时BE= ,易证△BQE∽△BDC,然后根据相似三角形的性质可得t的值;③当BP=PQ时,作PF⊥BC,垂足为F,此时BF= ,易证△BPF∽△BDC,然后根据相似三角形的性质可得t的值.
23.(1)24;9
(2)解:i)当 时,
ii)当 时, 由已知可得抛物线的顶点为
设解析式为 ,
图象经过
抛物线的解析式为:
综上所述, 点 在整个运动过程中 关于 的函数解析式为
(3)8;
解:(1)由题意,当t=4时,PC=4,由勾股定理得GP2=GC2+PC2=(2)2+42=24,S=GP2=24,故a=24.当t=1时,PC=1,GP2=GC2+PC2=(2)2+12=9,故S=9;
(3)如图所示,
当0≤t≤8时,图像关于直线x=4对称,且存在 三个时刻t1、t2、t3(t1<t2<t3)对应的正方形的面积均相等,故 t1+t2= 8;
当t>4时,,图像关于直线x=8对称,故t2+t3=16,
同时 t1+t2= 8, t3=4t1 ,
解得t3=,
代入函数解析式得S=
(1)由图像当t=4时,S=a,求出此时的PC的长得GP的平方,即为正方形的面积,同理当t=1时,求出GP2,即为面积;
(2)当t<4时,求出GP2的表达式,即为面积表达式;当t>4时,结合题意设顶点式,代入(4,24)即可求出解析式;
(3)结合图像的对称性知 t1+t2= 8,t2+t3=16,同时 t3=4t1,求出t3的值,代入函数解析式即可得对应的面积.
同课章节目录
