模型17 “一线三等角”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型17 “一线三等角”模型 (含答案)2025年中考数学几何模型专题复习 |
|
|
| 格式 | docx | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览



文档简介
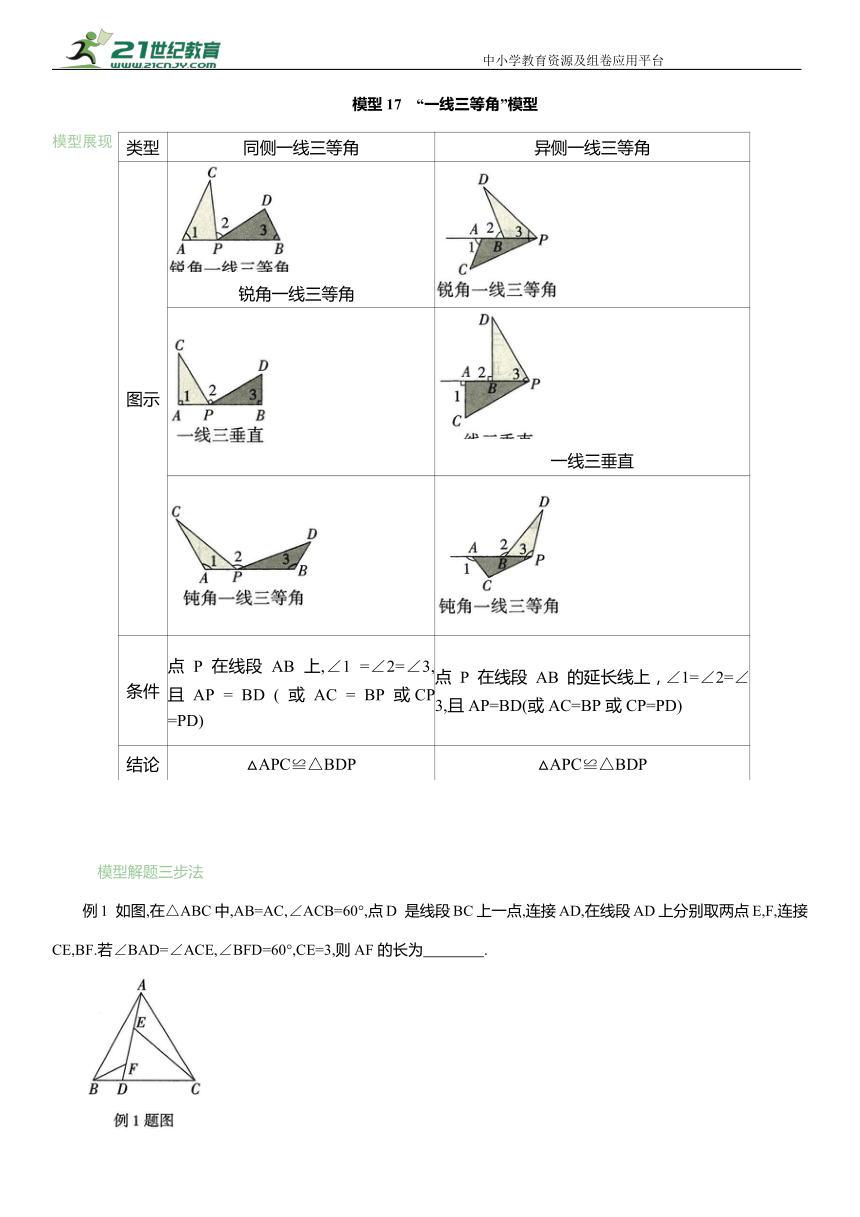
模型17 “一线三等角”模型
模型展现
模型解题三步法
例1 如图,在△ABC中,AB=AC,∠ACB=60°,点D 是线段BC上一点,连接AD,在线段AD上分别取两点E,F,连接CE,BF.若∠BAD=∠ACE,∠BFD=60°,CE=3,则AF的长为 .
例2 (模型构造) 如图,在矩形ABCD中,AB=4,BC=8,点E是BC上一点,且BE=3,连接AE,将线段AE绕点E 顺时针旋转90°得到线段 EF,连接CF,则△ECF 的面积为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,在△ABC 中,∠B=∠C,以点 C 为圆心,AB长为半径作圆,交BC 于点D,点E在AC上,连接AD,DE,若∠ADE=∠B,BC=7,CE=2,则AB的长为 ( )
A. 7 B. 6 C. 5 D. 4
2. 如图,在△ABC中,点D,E在边 BC上,连接EA,将线段 EA 绕点 E 逆时针旋转α得到EF,点F恰好在AB上,连接DF.若∠EDF= 与△ACE 的面积之和为7,则△AEF的面积为 ( )
A. 14 B. C. D. 7
3. 如图,在菱形ABCD 中,点 E 在 CD 边上,连接 AE,点 F, G 均在 AE 上,且∠BFE =∠DGE= ∠BAD,若∠BAD = 66°,∠ABF =19°,则∠AEC 的度数为 .
4.如图,在等腰直角△ABC中,BC=3,∠ACB=90°,点D 在AC上(不与A,C重合),且AD=1,连接BD,以DB为直角边向上作等腰直角△BDE,∠BDE=90°,连接CE,则CE的长为 .
5.如图,在正方形 ABCO 中,点O与坐标原点重合,点A,C分别在反比例函数 与 的图象上,若点C(1,4),则 的值为 .
6.如图,抛物线 与x轴交于A,B两点,与y轴交于点 C,点P 是抛物线对称轴上一点.连接 PC,将线段 PC绕点 P 旋转90°,得到线段 PQ,点 C 的对应点为 Q.当点 Q 在抛物线上时,求点 Q 的坐标.
模型17 “一线三等角”模型
模型展现
自主证明:
∵∠1=∠2,∠1+∠CAP=∠2+∠PBD,
∴∠PBD=∠CAP,
∵∠2=∠3,∠2=∠D+∠BPD,∠3=∠APC+∠BPD,
∴∠D=∠APC,
又∵AP=BD(或AC=BP 或CP=PD),
∴△APC≌△BDP.
模型解题三步法
例1 3 【解析】根据“一线三等角”模型得△BAF≌△ACE(AAS),∴AF=CE=3.
例2 AE=EF ∠ABC=∠AEF
152 【解析】如解图,过点 F作 FG⊥BC 于点 G.根据“一线三垂直”模型得△ABE≌△EGF(AAS),∴ BE=FG=3,∵ EC=BC-
题以类解
1. C 【解析】找模型:一线:线段BC;三个相等的角:∠ADE=∠B=∠C,等线段:AB=CD.抽离模型:如解图,用模型:根据同侧锐角“一线三等角”模型得△ABD≌△DCE(ASA),∴BD=CE=2,∴AB=CD=BC-BD=7-2=5.
2. B 【解析】找模型:一线:线段BC;三个相等的角:∠EDF =∠C=∠AEF,等线段:EF=AE.抽离模型:如解图,用模型:根据同侧钝角“一线三等角”模型得△FDE≌△ECA,∴S△AEC=S△EFD.∵△BFD 与△ACE的面积之和为7,∴△BFD与△EFD的面积之和为7.设△AEF 的底边 AF 上的高为 h,则△BEF的底边 BF上的高为h,.
3. 133° 【解析】∵ ∠BAF+∠FAD =∠BAD,∠ADG+∠FAD = ∠DGE,∠BAD = ∠DGE,∴∠BAF=∠ADG,∠BFA=∠AGD,在△ABF和△DAG 中,
△DAG(AAS)(异侧锐角“一线三等角”模型),∴ ∠ABF=∠DAG=19°,∵ ∠BAD=66°, 33° - 19°= 14°,∴ ∠AEC = 180° - 14°-33°=133°.
4. 【解析】如解图,过点 E 作 EF⊥AC 交AC的延长线于点 F,∴ ∠EFD =∠DCB =90°,∵∠BDE=90°,∴∠EDF+∠DEF=90°,∠EDF+∠BDC = 90°,∴ ∠DEF = ∠BDC,∵BD=DE,∴ △BDC≌△DEF(AAS)(异侧“一线三垂直”模型),∴BC=DF=3.∵AD=1,∴DC=AC-AD=BC-AD=2,∴EF=2,CF=DF-DC=BC-CD=1,∴在 Rt△CEF中,CE=
5.0 【解析】如解图,分别过点A,C作x轴的垂线与x轴交于点D,E.∵ ∠DAO+∠AOD=90°,∠AOD+∠COE = 90°,∴ ∠DAO = ∠COE,在△ADO 和△OEC中,
∴△ADO≌△OEC(AAS)(同侧“一线三垂直”模型),∴OE=AD,CE=OD,∴ ∣OE、 · 点 C(1,4),∴|OE·CE|=4=k ,∴|AD·DO|=|k |=4,∵点A在第二象限,∴ +4=0.
6. 解:令 解得
∴A(-3,0),B(1,0),
∵ PQ 由 PC 绕点 P 旋转 90°得到,
∴ △CPQ 是以 P 为直角顶点的等腰直角三角形.
∵抛物线的对称轴为直线x=-1,
∴设点 P 的坐标为(-1,p).
情况一:如解图①,当线段 PC 绕点 P 逆时针旋转90°时,分别过点 C,Q作对称轴的垂线,垂足分别为M,N,则∠CPM+∠PCM=90°.
∵∠CPQ=90°,∴∠CPM+∠QPN=90°,
∴∠PCM=∠QPN.
在△PCM 和△QPN中,
∴△PCM≌△QPN(AAS)
(同侧“一线三垂直”模型),
∵当x=0时,y=-3.
∴QN=PM=3+p,PN=CM=1,
∴点 Q 的坐标为(2+p,1+p),
将点Q(2+p,1+p)代入 中,
得
解得p=-1或p=-4(舍去),
∴点 Q 的坐标为(1,0);情况二:如解图②,作点C关于对称轴的对称点C',CC'交对称轴于点 R,在CC'上方取 PR=CR,∴P(-1,-2),此时点 Q与点 C'重合,∴点 Q 的坐标为(-2,-3);
情况三:当点 Q 为抛物线的顶点时,点Q 的坐标为(-1,-4),此时存在点 P(-1,-3),使得△CPQ 是以点 P 为直角顶点的等腰直角三角形;
情况四:当点 P 为抛物线的顶点时,即P(-1,-4),线段 PC 绕点 P 逆时针旋转90°,点C 与点 Q 关于对称轴对称,得Q(-2,-3),综上所述,点 Q 的坐标为(1,0)或(-2,-3)或(-1,-4).
模型展现
模型解题三步法
例1 如图,在△ABC中,AB=AC,∠ACB=60°,点D 是线段BC上一点,连接AD,在线段AD上分别取两点E,F,连接CE,BF.若∠BAD=∠ACE,∠BFD=60°,CE=3,则AF的长为 .
例2 (模型构造) 如图,在矩形ABCD中,AB=4,BC=8,点E是BC上一点,且BE=3,连接AE,将线段AE绕点E 顺时针旋转90°得到线段 EF,连接CF,则△ECF 的面积为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,在△ABC 中,∠B=∠C,以点 C 为圆心,AB长为半径作圆,交BC 于点D,点E在AC上,连接AD,DE,若∠ADE=∠B,BC=7,CE=2,则AB的长为 ( )
A. 7 B. 6 C. 5 D. 4
2. 如图,在△ABC中,点D,E在边 BC上,连接EA,将线段 EA 绕点 E 逆时针旋转α得到EF,点F恰好在AB上,连接DF.若∠EDF= 与△ACE 的面积之和为7,则△AEF的面积为 ( )
A. 14 B. C. D. 7
3. 如图,在菱形ABCD 中,点 E 在 CD 边上,连接 AE,点 F, G 均在 AE 上,且∠BFE =∠DGE= ∠BAD,若∠BAD = 66°,∠ABF =19°,则∠AEC 的度数为 .
4.如图,在等腰直角△ABC中,BC=3,∠ACB=90°,点D 在AC上(不与A,C重合),且AD=1,连接BD,以DB为直角边向上作等腰直角△BDE,∠BDE=90°,连接CE,则CE的长为 .
5.如图,在正方形 ABCO 中,点O与坐标原点重合,点A,C分别在反比例函数 与 的图象上,若点C(1,4),则 的值为 .
6.如图,抛物线 与x轴交于A,B两点,与y轴交于点 C,点P 是抛物线对称轴上一点.连接 PC,将线段 PC绕点 P 旋转90°,得到线段 PQ,点 C 的对应点为 Q.当点 Q 在抛物线上时,求点 Q 的坐标.
模型17 “一线三等角”模型
模型展现
自主证明:
∵∠1=∠2,∠1+∠CAP=∠2+∠PBD,
∴∠PBD=∠CAP,
∵∠2=∠3,∠2=∠D+∠BPD,∠3=∠APC+∠BPD,
∴∠D=∠APC,
又∵AP=BD(或AC=BP 或CP=PD),
∴△APC≌△BDP.
模型解题三步法
例1 3 【解析】根据“一线三等角”模型得△BAF≌△ACE(AAS),∴AF=CE=3.
例2 AE=EF ∠ABC=∠AEF
152 【解析】如解图,过点 F作 FG⊥BC 于点 G.根据“一线三垂直”模型得△ABE≌△EGF(AAS),∴ BE=FG=3,∵ EC=BC-
题以类解
1. C 【解析】找模型:一线:线段BC;三个相等的角:∠ADE=∠B=∠C,等线段:AB=CD.抽离模型:如解图,用模型:根据同侧锐角“一线三等角”模型得△ABD≌△DCE(ASA),∴BD=CE=2,∴AB=CD=BC-BD=7-2=5.
2. B 【解析】找模型:一线:线段BC;三个相等的角:∠EDF =∠C=∠AEF,等线段:EF=AE.抽离模型:如解图,用模型:根据同侧钝角“一线三等角”模型得△FDE≌△ECA,∴S△AEC=S△EFD.∵△BFD 与△ACE的面积之和为7,∴△BFD与△EFD的面积之和为7.设△AEF 的底边 AF 上的高为 h,则△BEF的底边 BF上的高为h,.
3. 133° 【解析】∵ ∠BAF+∠FAD =∠BAD,∠ADG+∠FAD = ∠DGE,∠BAD = ∠DGE,∴∠BAF=∠ADG,∠BFA=∠AGD,在△ABF和△DAG 中,
△DAG(AAS)(异侧锐角“一线三等角”模型),∴ ∠ABF=∠DAG=19°,∵ ∠BAD=66°, 33° - 19°= 14°,∴ ∠AEC = 180° - 14°-33°=133°.
4. 【解析】如解图,过点 E 作 EF⊥AC 交AC的延长线于点 F,∴ ∠EFD =∠DCB =90°,∵∠BDE=90°,∴∠EDF+∠DEF=90°,∠EDF+∠BDC = 90°,∴ ∠DEF = ∠BDC,∵BD=DE,∴ △BDC≌△DEF(AAS)(异侧“一线三垂直”模型),∴BC=DF=3.∵AD=1,∴DC=AC-AD=BC-AD=2,∴EF=2,CF=DF-DC=BC-CD=1,∴在 Rt△CEF中,CE=
5.0 【解析】如解图,分别过点A,C作x轴的垂线与x轴交于点D,E.∵ ∠DAO+∠AOD=90°,∠AOD+∠COE = 90°,∴ ∠DAO = ∠COE,在△ADO 和△OEC中,
∴△ADO≌△OEC(AAS)(同侧“一线三垂直”模型),∴OE=AD,CE=OD,∴ ∣OE、 · 点 C(1,4),∴|OE·CE|=4=k ,∴|AD·DO|=|k |=4,∵点A在第二象限,∴ +4=0.
6. 解:令 解得
∴A(-3,0),B(1,0),
∵ PQ 由 PC 绕点 P 旋转 90°得到,
∴ △CPQ 是以 P 为直角顶点的等腰直角三角形.
∵抛物线的对称轴为直线x=-1,
∴设点 P 的坐标为(-1,p).
情况一:如解图①,当线段 PC 绕点 P 逆时针旋转90°时,分别过点 C,Q作对称轴的垂线,垂足分别为M,N,则∠CPM+∠PCM=90°.
∵∠CPQ=90°,∴∠CPM+∠QPN=90°,
∴∠PCM=∠QPN.
在△PCM 和△QPN中,
∴△PCM≌△QPN(AAS)
(同侧“一线三垂直”模型),
∵当x=0时,y=-3.
∴QN=PM=3+p,PN=CM=1,
∴点 Q 的坐标为(2+p,1+p),
将点Q(2+p,1+p)代入 中,
得
解得p=-1或p=-4(舍去),
∴点 Q 的坐标为(1,0);情况二:如解图②,作点C关于对称轴的对称点C',CC'交对称轴于点 R,在CC'上方取 PR=CR,∴P(-1,-2),此时点 Q与点 C'重合,∴点 Q 的坐标为(-2,-3);
情况三:当点 Q 为抛物线的顶点时,点Q 的坐标为(-1,-4),此时存在点 P(-1,-3),使得△CPQ 是以点 P 为直角顶点的等腰直角三角形;
情况四:当点 P 为抛物线的顶点时,即P(-1,-4),线段 PC 绕点 P 逆时针旋转90°,点C 与点 Q 关于对称轴对称,得Q(-2,-3),综上所述,点 Q 的坐标为(1,0)或(-2,-3)或(-1,-4).
同课章节目录
