模型24 “两定点一定长”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型24 “两定点一定长”模型 (含答案)2025年中考数学几何模型专题复习 | 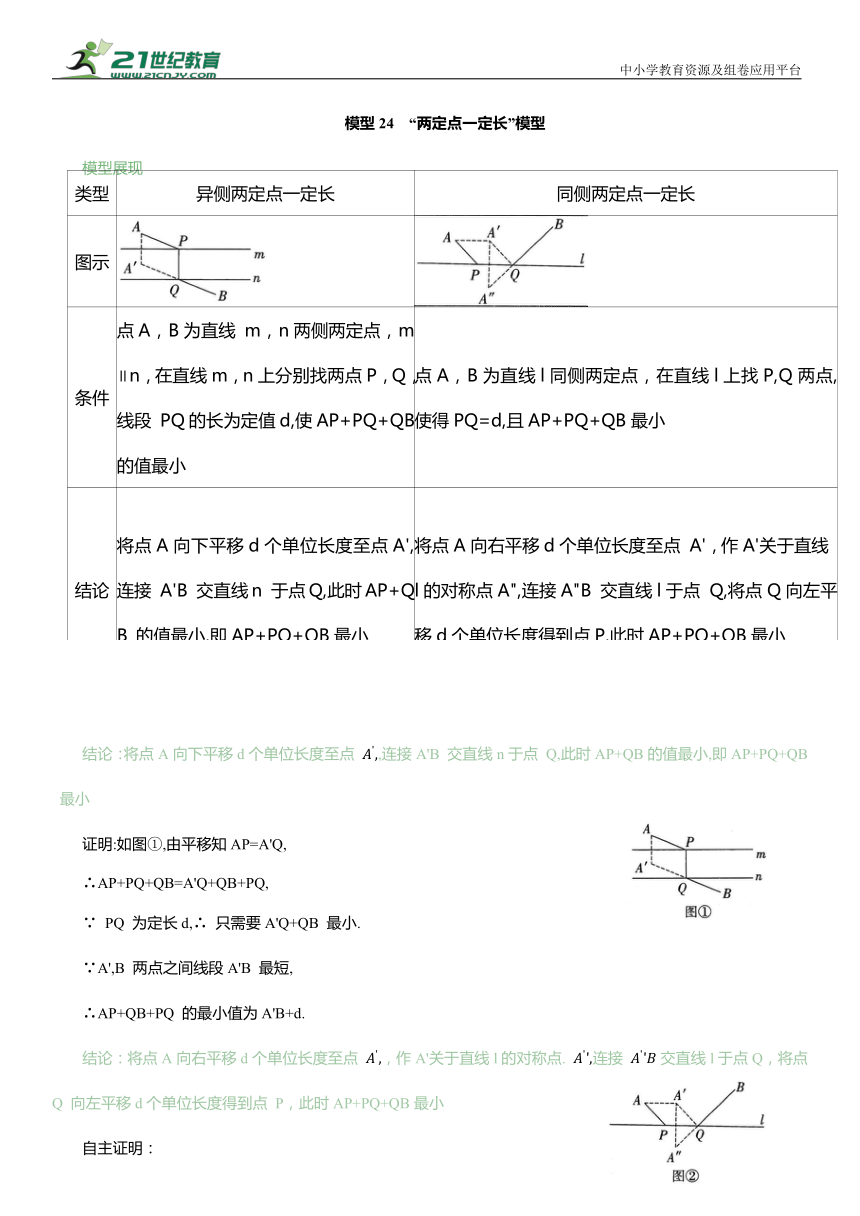 | |
| 格式 | docx | ||
| 文件大小 | 316.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 19:41:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
模型24 “两定点一定长”模型
模型展现
结论:将点A向下平移d个单位长度至点 ,连接A'B 交直线n于点 Q,此时AP+QB的值最小,即AP+PQ+QB 最小
证明:如图①,由平移知AP=A'Q,
∴AP+PQ+QB=A'Q+QB+PQ,
∵ PQ 为定长d,∴ 只需要A'Q+QB 最小.
∵A',B 两点之间线段A'B 最短,
∴AP+QB+PQ 的最小值为A'B+d.
结论:将点A向右平移d个单位长度至点 ,作A'关于直线l的对称点. 连接 交直线l于点Q,将点Q 向左平移d个单位长度得到点 P,此时AP+PQ+QB最小
自主证明:
模型解题三步法
例1 如图,菱形ABCD的边长为3,∠BAD=60°,点E,F在对角线AC上(点E在点F 的左侧),且EF=1,则DE+BF的最小值为 .
例2 如图,在正方形ABCD中,AB=8,点E在边 CD上,且CE=2,在边BC上取两点F,G(点F在点G左侧),且FG=2,则四边形AFGE 周长的最小值为 .
题以类解
1. 如图,正方形ABCD 的边长为2,点 E 是 BC上一点且不与点 B,C 重合,连接AE 交 BD于点 F. P 是边 CD 上一点,且 DP=2CP,Q为对角线BD上一点,且 则AF+PQ 的最小值为 .
2.如图,在直角坐标系中,矩形ABCD的顶点 A 在x轴的负半轴上,顶点 D在x轴的正半轴上,点 C(1,4),点A(-2,0),点 G是边 AB 的中点,线段EF 在边 AD上移动,且 EF=2,则当四边形 CGEF 的周长最小时,点E 的坐标为 .
3.如图,在扇形AOB中,∠AOB=90°,OA=6,点 C 为 OB 的中点,过点 C作 CD⊥OB交 于点D,点E,F均为线段 OA 上的动点,且点 F 在点 E 的下方, 连接 ED,FC,则四边形 CDEF周长的最小值为 .
4.如图,某景区为了增加景点特色,在景区修建了一条两河岸平行的人工河,凉亭A,B位于河两岸,为了游玩通行方便,现计划要在河上造一座桥(桥垂直于河岸),使凉亭A,B之间的路程最短.已知河宽为100 m,凉亭 A 到河岸 MN 的距离为 800 m,凉亭 B 到河岸PQ 的距离为400 m,且凉亭A,B 的水平距离为1600 m,则从凉亭A 出发经过桥后到达凉亭 B 的最短路程为 m.
模型展现
自主证明:
如图②,由平移知AP=A'Q,由轴对称的性质知A'Q=A"Q,即AP=A"Q,AP+PQ+QB=A"Q+QB+PQ,
∵ PQ 为定长d,
∴只需要A"Q+QB 最小,
∵A",B 两点之间线段A"B 最短,
∴AP+PQ+QB 的最小值为A"B+d.
模型解题三步法
例 1 【解析】根据“两定点一定长”模型作解图,四边形 DEFG 是平行四边形(一组对边平行且相等的四边形是平行四边形),∴DE=FG,∴DE+BF=FG+FB≥BG,连接BG交AC于点 F',连接BD交AC于点O,根据两点之间线段最短可知,此时 DE+FB 的值最小为 BG的长(异侧“两定点一定长”模型线段最短),∵ 四边形 ABCD 是菱形,AB=3,∠BAD=60°,∴AD=AB,∴△ABD 是等边三角形(有一个角为60°的等腰三角形是等边三角形),∴BD=AB=3,∵DG∥EF,BD⊥EF,∴ ∠GDB =∠DOC =90°. 在 Rt△BDG中, 即 DE+BF 的最小值为
例2 BC 点F 点G 点A 和点E
【解析】根据“两定点一定长”模型作解图,∴四边形AFGH 是平行四边形,∴HG=H'G=AF,∴AF+EG=H'G+EG,当E,G,H'三点共线时,AF+EG有最小值,过点 H'作H'I⊥DC 交DC 的延长线于点I,∵AB=8,CE=2,∴EI=10,∵FG=2,∴AH=2,∴H'I=6,在 Rt△EH'I 中, DE=6,AD=8,∴AE=10,∴四边形AFGE 周长的最小值为
题以类解
【解析】找模型:是否存在有两动点的直线:BD,动点:点F,点Q;两动点间的距离是否固定: 线段BD外是否存在两定点:点A 和点 P;是否求最值:AF+PQ 的最小值.抽离模型.如解图.用模型:根据“两定点一定长”模型作解图,将点P 沿着与BD 平行的方向平移FQ 的长度,交 BC于点 E,连接 PE.∴ PE=QF,PE∥BD,∴四边形FEPQ 是平行四边形(一组对边平行且相等的四边形是平行四边形),∴ QP=FE,∵AF+PQ=AF+FE≥AE,∴AF+PQ 的最小值为AE 的长,∵PE∥BD,∴△CPE∽△CDB,∵.DP=2CP,∴CE=CP=
【解析】找模型:是否存在有两动点的直线:AD,动点:点E,点F;两动点间的距离是否固定:EF=2;线段AD 外是否存在两定点:点G 和点 C;是否求最值:四边形CGEF 周长的最小值.抽离模型:如解图.用模型:根据“两定点一定长”模型作解图,将点 C 向左平移2个单位长度至点 M,作点 G关于x轴的对称点 G',连接G'E,G'M,ME.则 CM=EF且点 M 的坐标为(-1,4),G'的坐标为(-2,-2),∵四边形 ABCD 是矩形,∴BC∥AD,∴四边形 CMEF 为平行四边形(一组对边平行且相等的四边形是平行四边形),∴CF=ME,∴CF+GE=ME+GE,∵点 G和G'关于x轴对称,∴EG=EG',∵CG,EF都是固定值,∴当M,E,G'三点在同一条直线上时,CF+GE=ME+GE=ME+G'E 最小(同侧“两定点一定长”模型线段最短),设直线MG'的解析式为y= kx+b(k≠0),把 M(-1,4), G'(-2,-2)代入得 解得 直线MG'的解析式为y=6x+10,当y=0时, .点 E 的坐标为
3. 8 【解析】如解图,作点 C 关于 OA 的对称点 C',将点 C'向上平移 个单位长度为点 D',作点 D'关于AO 的对称点 M,则( D'M=6,连接C'D',则C'D'∥OA,连接DD'交OA 于点 E,在点 E 的下方截取. 连接C'F,此时,四边形 C'D'EF 是平行四边形,则CF=C'F=D'E,四边形 CDEF 的周长最小,最小值为 EF+CD+DD'(同侧“两定点一定长”模型线段最短),连接 OD,则OA=OB=OD=6(扇形半径相等),∵ OC= 4 ,∴四边形 CDEF 周长的最小值为 EF+CD
4. 2100 【解析】如解图,将点 A 向下平移100m至点F 处,连接FB 交 PQ 于点 D',过点 D'作D'C'⊥MN 于点 C',延长 AF 交 MN 于点 E,交 PQ 于点 G.那么 D'C'就是造桥的位置,此时从凉亭A 出发经过桥后到达凉亭 B 的路程最短. ∵ AF =C'D',AF∥C'D',∴ 四边形FD'C'A是平行四边形(一组对边平行且相等的四边形是平行四边形), C'D',过点B 作BH∥PQ交AG的延长线于点H,由题意可得 HB = 1600 m,AE = 800 m,GH=400m,EG=C'D'=100m,∴EF=AE-AF=700 m,∴FH=EF+EG+GH=1200 m,在Rt△FHB中,由勾股定理得 2000+100=2100 m,∴从凉亭A 出发经过桥后到达凉亭 B 的最短路程为2100 m.
模型24 “两定点一定长”模型
模型展现
结论:将点A向下平移d个单位长度至点 ,连接A'B 交直线n于点 Q,此时AP+QB的值最小,即AP+PQ+QB 最小
证明:如图①,由平移知AP=A'Q,
∴AP+PQ+QB=A'Q+QB+PQ,
∵ PQ 为定长d,∴ 只需要A'Q+QB 最小.
∵A',B 两点之间线段A'B 最短,
∴AP+QB+PQ 的最小值为A'B+d.
结论:将点A向右平移d个单位长度至点 ,作A'关于直线l的对称点. 连接 交直线l于点Q,将点Q 向左平移d个单位长度得到点 P,此时AP+PQ+QB最小
自主证明:
模型解题三步法
例1 如图,菱形ABCD的边长为3,∠BAD=60°,点E,F在对角线AC上(点E在点F 的左侧),且EF=1,则DE+BF的最小值为 .
例2 如图,在正方形ABCD中,AB=8,点E在边 CD上,且CE=2,在边BC上取两点F,G(点F在点G左侧),且FG=2,则四边形AFGE 周长的最小值为 .
题以类解
1. 如图,正方形ABCD 的边长为2,点 E 是 BC上一点且不与点 B,C 重合,连接AE 交 BD于点 F. P 是边 CD 上一点,且 DP=2CP,Q为对角线BD上一点,且 则AF+PQ 的最小值为 .
2.如图,在直角坐标系中,矩形ABCD的顶点 A 在x轴的负半轴上,顶点 D在x轴的正半轴上,点 C(1,4),点A(-2,0),点 G是边 AB 的中点,线段EF 在边 AD上移动,且 EF=2,则当四边形 CGEF 的周长最小时,点E 的坐标为 .
3.如图,在扇形AOB中,∠AOB=90°,OA=6,点 C 为 OB 的中点,过点 C作 CD⊥OB交 于点D,点E,F均为线段 OA 上的动点,且点 F 在点 E 的下方, 连接 ED,FC,则四边形 CDEF周长的最小值为 .
4.如图,某景区为了增加景点特色,在景区修建了一条两河岸平行的人工河,凉亭A,B位于河两岸,为了游玩通行方便,现计划要在河上造一座桥(桥垂直于河岸),使凉亭A,B之间的路程最短.已知河宽为100 m,凉亭 A 到河岸 MN 的距离为 800 m,凉亭 B 到河岸PQ 的距离为400 m,且凉亭A,B 的水平距离为1600 m,则从凉亭A 出发经过桥后到达凉亭 B 的最短路程为 m.
模型展现
自主证明:
如图②,由平移知AP=A'Q,由轴对称的性质知A'Q=A"Q,即AP=A"Q,AP+PQ+QB=A"Q+QB+PQ,
∵ PQ 为定长d,
∴只需要A"Q+QB 最小,
∵A",B 两点之间线段A"B 最短,
∴AP+PQ+QB 的最小值为A"B+d.
模型解题三步法
例 1 【解析】根据“两定点一定长”模型作解图,四边形 DEFG 是平行四边形(一组对边平行且相等的四边形是平行四边形),∴DE=FG,∴DE+BF=FG+FB≥BG,连接BG交AC于点 F',连接BD交AC于点O,根据两点之间线段最短可知,此时 DE+FB 的值最小为 BG的长(异侧“两定点一定长”模型线段最短),∵ 四边形 ABCD 是菱形,AB=3,∠BAD=60°,∴AD=AB,∴△ABD 是等边三角形(有一个角为60°的等腰三角形是等边三角形),∴BD=AB=3,∵DG∥EF,BD⊥EF,∴ ∠GDB =∠DOC =90°. 在 Rt△BDG中, 即 DE+BF 的最小值为
例2 BC 点F 点G 点A 和点E
【解析】根据“两定点一定长”模型作解图,∴四边形AFGH 是平行四边形,∴HG=H'G=AF,∴AF+EG=H'G+EG,当E,G,H'三点共线时,AF+EG有最小值,过点 H'作H'I⊥DC 交DC 的延长线于点I,∵AB=8,CE=2,∴EI=10,∵FG=2,∴AH=2,∴H'I=6,在 Rt△EH'I 中, DE=6,AD=8,∴AE=10,∴四边形AFGE 周长的最小值为
题以类解
【解析】找模型:是否存在有两动点的直线:BD,动点:点F,点Q;两动点间的距离是否固定: 线段BD外是否存在两定点:点A 和点 P;是否求最值:AF+PQ 的最小值.抽离模型.如解图.用模型:根据“两定点一定长”模型作解图,将点P 沿着与BD 平行的方向平移FQ 的长度,交 BC于点 E,连接 PE.∴ PE=QF,PE∥BD,∴四边形FEPQ 是平行四边形(一组对边平行且相等的四边形是平行四边形),∴ QP=FE,∵AF+PQ=AF+FE≥AE,∴AF+PQ 的最小值为AE 的长,∵PE∥BD,∴△CPE∽△CDB,∵.DP=2CP,∴CE=CP=
【解析】找模型:是否存在有两动点的直线:AD,动点:点E,点F;两动点间的距离是否固定:EF=2;线段AD 外是否存在两定点:点G 和点 C;是否求最值:四边形CGEF 周长的最小值.抽离模型:如解图.用模型:根据“两定点一定长”模型作解图,将点 C 向左平移2个单位长度至点 M,作点 G关于x轴的对称点 G',连接G'E,G'M,ME.则 CM=EF且点 M 的坐标为(-1,4),G'的坐标为(-2,-2),∵四边形 ABCD 是矩形,∴BC∥AD,∴四边形 CMEF 为平行四边形(一组对边平行且相等的四边形是平行四边形),∴CF=ME,∴CF+GE=ME+GE,∵点 G和G'关于x轴对称,∴EG=EG',∵CG,EF都是固定值,∴当M,E,G'三点在同一条直线上时,CF+GE=ME+GE=ME+G'E 最小(同侧“两定点一定长”模型线段最短),设直线MG'的解析式为y= kx+b(k≠0),把 M(-1,4), G'(-2,-2)代入得 解得 直线MG'的解析式为y=6x+10,当y=0时, .点 E 的坐标为
3. 8 【解析】如解图,作点 C 关于 OA 的对称点 C',将点 C'向上平移 个单位长度为点 D',作点 D'关于AO 的对称点 M,则( D'M=6,连接C'D',则C'D'∥OA,连接DD'交OA 于点 E,在点 E 的下方截取. 连接C'F,此时,四边形 C'D'EF 是平行四边形,则CF=C'F=D'E,四边形 CDEF 的周长最小,最小值为 EF+CD+DD'(同侧“两定点一定长”模型线段最短),连接 OD,则OA=OB=OD=6(扇形半径相等),∵ OC= 4 ,∴四边形 CDEF 周长的最小值为 EF+CD
4. 2100 【解析】如解图,将点 A 向下平移100m至点F 处,连接FB 交 PQ 于点 D',过点 D'作D'C'⊥MN 于点 C',延长 AF 交 MN 于点 E,交 PQ 于点 G.那么 D'C'就是造桥的位置,此时从凉亭A 出发经过桥后到达凉亭 B 的路程最短. ∵ AF =C'D',AF∥C'D',∴ 四边形FD'C'A是平行四边形(一组对边平行且相等的四边形是平行四边形), C'D',过点B 作BH∥PQ交AG的延长线于点H,由题意可得 HB = 1600 m,AE = 800 m,GH=400m,EG=C'D'=100m,∴EF=AE-AF=700 m,∴FH=EF+EG+GH=1200 m,在Rt△FHB中,由勾股定理得 2000+100=2100 m,∴从凉亭A 出发经过桥后到达凉亭 B 的最短路程为2100 m.
同课章节目录
