模型25 “勾股树” (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型25 “勾股树” (含答案)2025年中考数学几何模型专题复习 |
|
|
| 格式 | docx | ||
| 文件大小 | 330.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型25 “勾股树”
模型展现
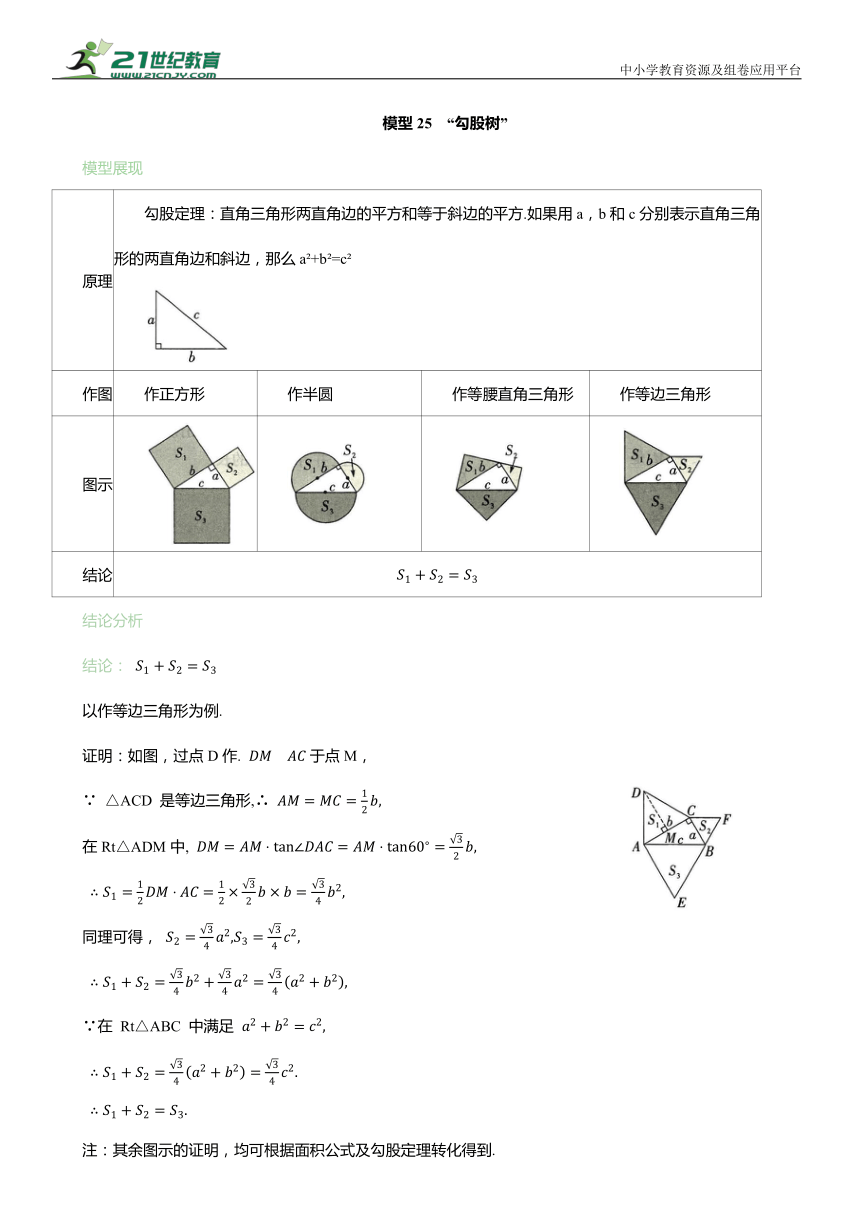
原理 勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a +b =c
作图 作正方形 作半圆 作等腰直角三角形 作等边三角形
图示
结论
结论分析
结论:
以作等边三角形为例.
证明:如图,过点D作. 于点M,
∵ △ACD 是等边三角形,∴
在Rt△ADM中,
同理可得,
∵在 Rt△ABC 中满足
注:其余图示的证明,均可根据面积公式及勾股定理转化得到.
模型解题三步法
例 如图,分别以 的三边为斜边向外作等腰直角三角形,若图中阴影部分的面积为100,则AF的长为 ( )
A. 10 C. 20
题以类解
1. 如图,直线l上有三个正方形a,b,c,若b,c的面积分别为8和5,则a的面积为( )
A. 2 C. 3 D. 4
2.如图,以AC 为直径画半圆,在半圆上取一点 B,连接AB,BC,分别以AB,BC为直径画半圆,则图中阴影部分的面积与△ABC的面积关系为 ( )
3. 数学课上王老师和学生一起探究勾股定理和面积的拓展问题时,分别以直角三角形 ABC 的三条边为边向外作等边三角形,如图①,图中的 S ,S ,S 满足的数量关系是 ;如图②,将△ABF 沿着 AB 翻折得到△ABF',若 ,则△ABC 的面积是 .
4. 某数学课外活动小组在学习了勾股定理之后,探究以四边形四条边向外作形状相同的图形的面积关系.
【问题提出】
如图①,在四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,若 求S 的值;
【拓展延伸】
如图②,在四边形ABCD中,AD∥BC,∠ABC+ ,分别以AB,AD,CD为边向四边形外作正方形,其面积分别为 求证:
模型解题三步法
例 A 【解析】根据“勾股树”模型得S△ACD+ ∴2S△ABF=100,即,S△ABF=50,∵△ABF为等腰直角三角形, 解得AF=10(负值已舍去).
题以类解
1. C 【解析】找模型:是否存在直角三角形:Rt△ABC,是否以直角三角形三边向外作形状
相同的图形:作正方形.构造模型:如解图,以BC 为边作正方形.∵ ∠ACB+∠ECD=90°,∠CED+∠ECD=90°,∴∠ACB= ∠CED, 在△ABC 和△CDE 中 ≌△CDE(AAS),∴BC=DE,用模型:
2. B 【解析】找模型:是否存在直角三角形:Rt△ABC,是否以直角三角形三边向外作形状相同的图形:作半圆.构造模型:补全模型如解图.用模型:设以AB,BC,AC为直径的半圆面积分别为S ,S ,S ,根据“勾股树”模型得
10 【解析】根据“勾股树”模型得 ;如解图,设△ABC 的面积为 S,2个空白小三角形的面积分别为a,b,∴S +
4.【问题提出】
解:由题意得
如解图①,连接AC,
在Rt△ADC 和Rt△ABC中,
即
【拓展延伸】
证明:如解图②,过 D 点作 DE∥AB,交 BC 于点E,设四边形的边AB,DC,AD的长分别为a,b,c,∵AD∥BC,
∴四边形ADEB 为平行四边形(两组对边分别平行的四边形是平行四边形),
∴AD=BE,
∵BC=2AD,
∴ EC=AD=c,DE=AB=a,∠EDC =180°-(∠DEC+∠BCD)= 180°-(∠ABC+∠BCD)=90°,则
模型25 “勾股树”
模型展现
原理 勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a +b =c
作图 作正方形 作半圆 作等腰直角三角形 作等边三角形
图示
结论
结论分析
结论:
以作等边三角形为例.
证明:如图,过点D作. 于点M,
∵ △ACD 是等边三角形,∴
在Rt△ADM中,
同理可得,
∵在 Rt△ABC 中满足
注:其余图示的证明,均可根据面积公式及勾股定理转化得到.
模型解题三步法
例 如图,分别以 的三边为斜边向外作等腰直角三角形,若图中阴影部分的面积为100,则AF的长为 ( )
A. 10 C. 20
题以类解
1. 如图,直线l上有三个正方形a,b,c,若b,c的面积分别为8和5,则a的面积为( )
A. 2 C. 3 D. 4
2.如图,以AC 为直径画半圆,在半圆上取一点 B,连接AB,BC,分别以AB,BC为直径画半圆,则图中阴影部分的面积与△ABC的面积关系为 ( )
3. 数学课上王老师和学生一起探究勾股定理和面积的拓展问题时,分别以直角三角形 ABC 的三条边为边向外作等边三角形,如图①,图中的 S ,S ,S 满足的数量关系是 ;如图②,将△ABF 沿着 AB 翻折得到△ABF',若 ,则△ABC 的面积是 .
4. 某数学课外活动小组在学习了勾股定理之后,探究以四边形四条边向外作形状相同的图形的面积关系.
【问题提出】
如图①,在四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,若 求S 的值;
【拓展延伸】
如图②,在四边形ABCD中,AD∥BC,∠ABC+ ,分别以AB,AD,CD为边向四边形外作正方形,其面积分别为 求证:
模型解题三步法
例 A 【解析】根据“勾股树”模型得S△ACD+ ∴2S△ABF=100,即,S△ABF=50,∵△ABF为等腰直角三角形, 解得AF=10(负值已舍去).
题以类解
1. C 【解析】找模型:是否存在直角三角形:Rt△ABC,是否以直角三角形三边向外作形状
相同的图形:作正方形.构造模型:如解图,以BC 为边作正方形.∵ ∠ACB+∠ECD=90°,∠CED+∠ECD=90°,∴∠ACB= ∠CED, 在△ABC 和△CDE 中 ≌△CDE(AAS),∴BC=DE,用模型:
2. B 【解析】找模型:是否存在直角三角形:Rt△ABC,是否以直角三角形三边向外作形状相同的图形:作半圆.构造模型:补全模型如解图.用模型:设以AB,BC,AC为直径的半圆面积分别为S ,S ,S ,根据“勾股树”模型得
10 【解析】根据“勾股树”模型得 ;如解图,设△ABC 的面积为 S,2个空白小三角形的面积分别为a,b,∴S +
4.【问题提出】
解:由题意得
如解图①,连接AC,
在Rt△ADC 和Rt△ABC中,
即
【拓展延伸】
证明:如解图②,过 D 点作 DE∥AB,交 BC 于点E,设四边形的边AB,DC,AD的长分别为a,b,c,∵AD∥BC,
∴四边形ADEB 为平行四边形(两组对边分别平行的四边形是平行四边形),
∴AD=BE,
∵BC=2AD,
∴ EC=AD=c,DE=AB=a,∠EDC =180°-(∠DEC+∠BCD)= 180°-(∠ABC+∠BCD)=90°,则
同课章节目录
