模型23 “两点两线”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型23 “两点两线”模型 (含答案)2025年中考数学几何模型专题复习 | 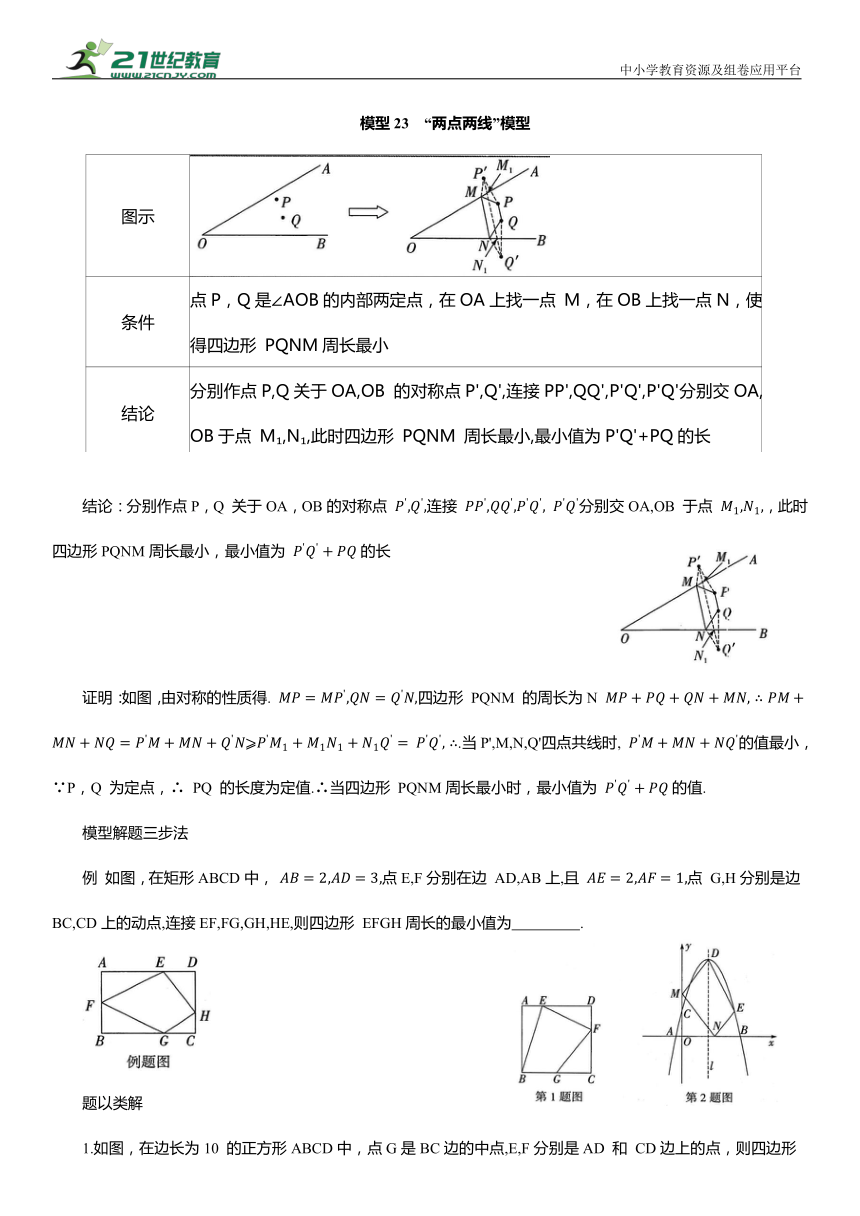 | |
| 格式 | docx | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 19:51:18 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
模型23 “两点两线”模型
结论:分别作点P,Q 关于OA,OB的对称点 连接 分别交OA,OB 于点 ,此时四边形PQNM周长最小,最小值为 的长
证明:如图,由对称的性质得. 四边形 PQNM 的周长为N .当P',M,N,Q'四点共线时, 的值最小,∵P,Q 为定点,∴ PQ 的长度为定值.∴当四边形 PQNM周长最小时,最小值为 的值.
模型解题三步法
例 如图,在矩形ABCD中, 点E,F分别在边 AD,AB上,且 点 G,H分别是边 BC,CD上的动点,连接EF,FG,GH,HE,则四边形 EFGH周长的最小值为 .
题以类解
1.如图,在边长为10 的正方形ABCD中,点G是BC边的中点,E,F分别是AD 和 CD边上的点,则四边形 BEFG周长的最小值为 .
2. 如图,抛物线 与x轴交于点A,B,与y轴交于点 C,抛物线的对称轴为直线l,顶点为点 D,点C 关于直线l的对称点为点E.若点M为y轴上一动点,点 N 为x 轴上一动点,则四边形 DENM 周长的最小值为 .
3. 如图,在 中,∠C=90°,E,F 为AB上两点, 若G,H分别为AC,BC上的两个动点,则四边形EGHF周长的最小值为 .
模型解题三步法
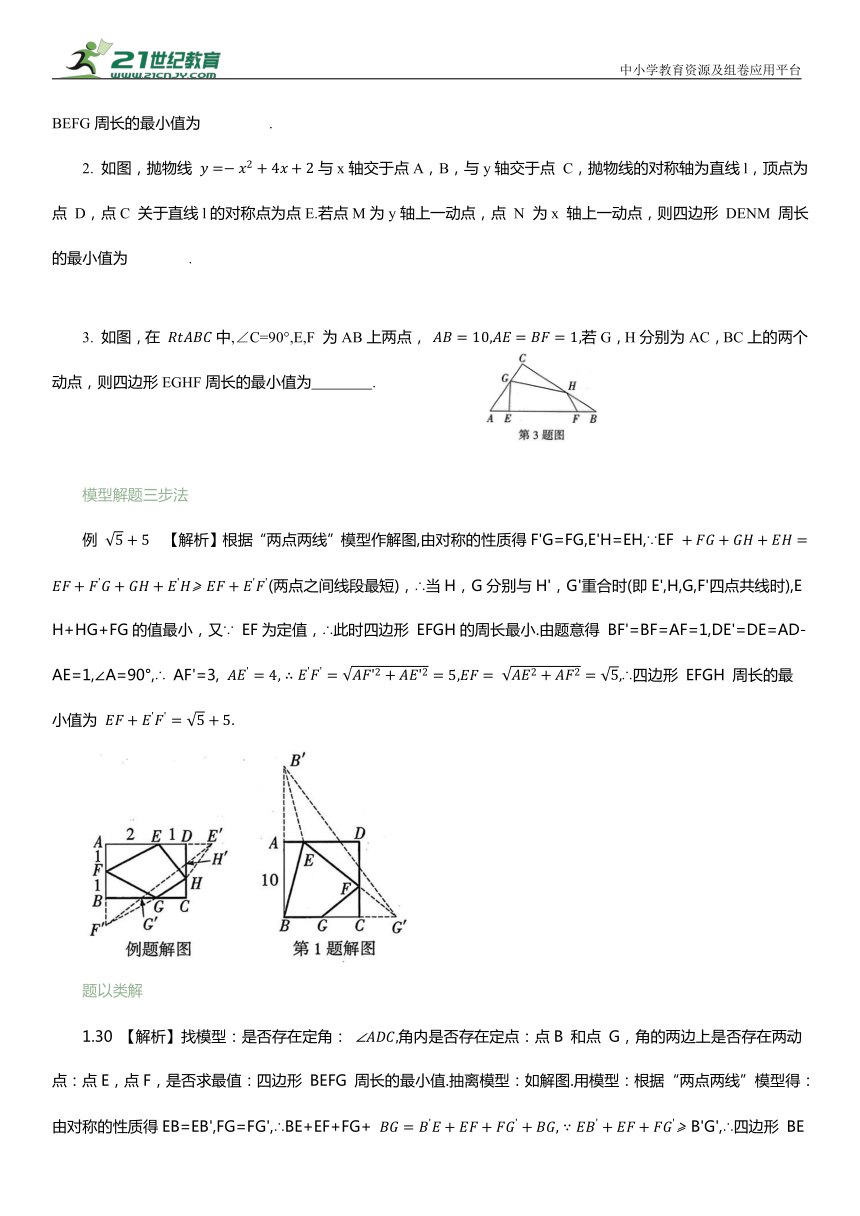
例 【解析】根据“两点两线”模型作解图,由对称的性质得F'G=FG,E'H=EH,∵EF (两点之间线段最短),∴当H,G分别与H',G'重合时(即E',H,G,F'四点共线时),EH+HG+FG的值最小,又∵ EF为定值,∴此时四边形 EFGH的周长最小.由题意得 BF'=BF=AF=1,DE'=DE=AD-AE=1,∠A=90°,∴ AF'=3, ∴四边形 EFGH 周长的最小值为
题以类解
1.30 【解析】找模型:是否存在定角: 角内是否存在定点:点B 和点 G,角的两边上是否存在两动点:点E,点F,是否求最值:四边形 BEFG 周长的最小值.抽离模型:如解图.用模型:根据“两点两线”模型得:由对称的性质得EB=EB',FG=FG',∴BE+EF+FG+ B'G',∴四边形 BEFG周长的最小值为 BG+B'G',∵G为BC的中点,GC=G'C,AB=AB', ∵在正方形ABCD 中,∠ABC=90°,∴ 在 Rt△B'BG'中, ∴四边形 BEFG的周长的最小值为25+5=30.
【解析】找模型:是否存在定角:∠xOy,角内是否存在定点:点 D 和点 E,角的两边上是否存在两动点:点M,点N,是否求最值:四边形 DENM 周长的最小值.抽离模型:如解图.用模型:根据“两点两线”模型得:由对称的性质得 DM=D'M,NE=NE', ∴当D',M,N,E'四点共线时,DM+MN+NE 的值最小(“两点两线”型线段最短),此时四边形 DENM的周长最小,易得D(2,6),E(4,2),∴D'(-2, .四边形DENM 周长的最小值为
3. 18 【解析】如解图,分别作点 E,F关于AC,BC 的对称点 E',F',连接 EE',FF',连接E'F'交AC 于点 G',交BC 于点 H',连接AE',E'G,BF',F'H,则E'G=EG,F'H=FH,∴四边形 EGHF 的周长为 EF+EG+GH+HF=EF+ 当E',G,H,F'四点共线时,四边形 EGHF 的周长有最小值,即EF+E'F'的值(“两点两线”模型线段最短),∵AB=10,AE=BF=1,∴EF=8,由对称可知AE=AE'=BF=BF',∠E'AC=∠EAC,∠FBC=∠F'BC,∵∠C=90°,∴ ∠CAB+∠CBA=90°,∴ ∠E'AE+∠F'BF =2(∠CAB+∠CBA)=180°,∴E'A∥BF',∴四边形AE'F'B 是平行四边形(一组对边平行且相等的四边形是平行四边形),∴ E' F' = AB = 10,∴ 四边形EGHF 周长的最小值为8+10=18.
模型23 “两点两线”模型
结论:分别作点P,Q 关于OA,OB的对称点 连接 分别交OA,OB 于点 ,此时四边形PQNM周长最小,最小值为 的长
证明:如图,由对称的性质得. 四边形 PQNM 的周长为N .当P',M,N,Q'四点共线时, 的值最小,∵P,Q 为定点,∴ PQ 的长度为定值.∴当四边形 PQNM周长最小时,最小值为 的值.
模型解题三步法
例 如图,在矩形ABCD中, 点E,F分别在边 AD,AB上,且 点 G,H分别是边 BC,CD上的动点,连接EF,FG,GH,HE,则四边形 EFGH周长的最小值为 .
题以类解
1.如图,在边长为10 的正方形ABCD中,点G是BC边的中点,E,F分别是AD 和 CD边上的点,则四边形 BEFG周长的最小值为 .
2. 如图,抛物线 与x轴交于点A,B,与y轴交于点 C,抛物线的对称轴为直线l,顶点为点 D,点C 关于直线l的对称点为点E.若点M为y轴上一动点,点 N 为x 轴上一动点,则四边形 DENM 周长的最小值为 .
3. 如图,在 中,∠C=90°,E,F 为AB上两点, 若G,H分别为AC,BC上的两个动点,则四边形EGHF周长的最小值为 .
模型解题三步法
例 【解析】根据“两点两线”模型作解图,由对称的性质得F'G=FG,E'H=EH,∵EF (两点之间线段最短),∴当H,G分别与H',G'重合时(即E',H,G,F'四点共线时),EH+HG+FG的值最小,又∵ EF为定值,∴此时四边形 EFGH的周长最小.由题意得 BF'=BF=AF=1,DE'=DE=AD-AE=1,∠A=90°,∴ AF'=3, ∴四边形 EFGH 周长的最小值为
题以类解
1.30 【解析】找模型:是否存在定角: 角内是否存在定点:点B 和点 G,角的两边上是否存在两动点:点E,点F,是否求最值:四边形 BEFG 周长的最小值.抽离模型:如解图.用模型:根据“两点两线”模型得:由对称的性质得EB=EB',FG=FG',∴BE+EF+FG+ B'G',∴四边形 BEFG周长的最小值为 BG+B'G',∵G为BC的中点,GC=G'C,AB=AB', ∵在正方形ABCD 中,∠ABC=90°,∴ 在 Rt△B'BG'中, ∴四边形 BEFG的周长的最小值为25+5=30.
【解析】找模型:是否存在定角:∠xOy,角内是否存在定点:点 D 和点 E,角的两边上是否存在两动点:点M,点N,是否求最值:四边形 DENM 周长的最小值.抽离模型:如解图.用模型:根据“两点两线”模型得:由对称的性质得 DM=D'M,NE=NE', ∴当D',M,N,E'四点共线时,DM+MN+NE 的值最小(“两点两线”型线段最短),此时四边形 DENM的周长最小,易得D(2,6),E(4,2),∴D'(-2, .四边形DENM 周长的最小值为
3. 18 【解析】如解图,分别作点 E,F关于AC,BC 的对称点 E',F',连接 EE',FF',连接E'F'交AC 于点 G',交BC 于点 H',连接AE',E'G,BF',F'H,则E'G=EG,F'H=FH,∴四边形 EGHF 的周长为 EF+EG+GH+HF=EF+ 当E',G,H,F'四点共线时,四边形 EGHF 的周长有最小值,即EF+E'F'的值(“两点两线”模型线段最短),∵AB=10,AE=BF=1,∴EF=8,由对称可知AE=AE'=BF=BF',∠E'AC=∠EAC,∠FBC=∠F'BC,∵∠C=90°,∴ ∠CAB+∠CBA=90°,∴ ∠E'AE+∠F'BF =2(∠CAB+∠CBA)=180°,∴E'A∥BF',∴四边形AE'F'B 是平行四边形(一组对边平行且相等的四边形是平行四边形),∴ E' F' = AB = 10,∴ 四边形EGHF 周长的最小值为8+10=18.
同课章节目录
