2025年九年级数学中考三轮冲刺训练四边形有关的综合问题
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练四边形有关的综合问题 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练四边形有关的综合问题
一、选择题
1.如图,在正方形ABCD中,以AB为边作等边三角形ABP,连接AC,PD,PC,则下列结论;①∠BCP=75°;②△ADP≌△BCP;③△ADP和△ABC的面积比为1:2;④.其中结论正确的序号有( )
A.①②④ B.②③ C.①③④ D.①②③④
2.如图,正方形ABCD中,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE.延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠GAE=45°;③BG=GC;④AG∥CF;⑤△GCF是等边三角形,其中正确结论有( )个.
A.2 B.3 C.4 D.5
3.如图,正方形ABCD的边长为12,E为CD的中点,连接BD,AE交于点F,连接CF,则tan∠FCD的值为( )
A. B. C. D.
4.如图,点E在正方形ABCD的内部,且△ABE是等边三角形,连接BD,DE,则∠BDE=( )
A.37.5° B.35° C.30° D.25°
5.2024年6月2日6时23分,嫦娥六号着陆器和上升器组合体在鹊桥二号中继星的支持下,成功着陆在月球背面南极一艾特肯盆地预选着陆区.组合体元件中有个展板的平面图如图所示,在正方形ABCD中,E,F分别是BC,AB上的点,DE,CF相交于点M.N是DF的中点,若AF=1,CE=BF=2,则MN的长为( )
A. B. C.2 D.
6.如图所示,已知∠KEF=120°,则∠A+∠B+∠C+∠D+∠H+∠G+∠M+∠N=( )
A.540° B.600° C.620° D.720°
7.如图,正方形ABCD的对角线BD上有一点E,满足DE=2BE,连接CE,过D作DF⊥CE 于F,连接BF.则的值为( )
A. B. C. D.
8.如图,正方形CEDF的顶点D,E,F分别在△ABC的边AB,BC,AC上.AD=5,DB=3,则△AFD与△BDE面积之和等于( )
A.5.5 B.6 C.7.5 D.8
9.如图,在 ABCD中,∠C=120°,AB=8,AD>AB,H、G分别是CD、BC上的动点,连接AH、GH,E、F分别为AH、GH的中点,则EF的最小值是( )
A.4 B.5 C. D.
10.如图,在一个大长方形中放入了标号为①,②,③,④,⑤五个四边形,其中①,②为两个长方形,③,④,⑤为三个正方形,相邻图形之间互不重叠也无缝隙.若想求得长方形②的周长,甲、乙、丙、丁四位同学提出了自己的想法:
甲说:只需要知道①与③的周长和;乙说:只需要知道①与⑤的周长和;
丙说:只需要知道③与④的周长和;丁说:只需要知道⑤与①的周长差.
下列说法正确的是( )
A.只有甲正确 B.甲和乙均正确
C.乙和丙均正确 D.只有丁正确
二、填空题
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为斜边BC上的一个动点,过P分别作PE⊥AB于点E,作PF⊥AC于点F,连接EF,则线段EF的最小值为 .
12.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为 .
13.如图,已知菱形ABCD的边长为2°,点G、E、F分别是BD、AB、AD上的点,若GE+GF=3,则AE+AF的值是 .
14.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
15.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D 的坐标是 .
16.如图,在矩形ABCD中,E,F是边BC上两点,且BE=EF=FC,连接DE,AF,DE与AF相交于点G,连接BG.若AB=4,BC=6,则cos∠GBF的值为 .
17.如图,在正方形ABCD中,点E、F分别是边BC、CD上的两个点,连接AE、AF分别与对角线BD交于点G、H,连接GF,若AG⊥GF,DHBG,下列说法正确的序号是 .
①AG=FG;②BG2+DH2=GH2;③∠BGE=60°;④若CE=3,BE+DF值为3.
18.如图,在正方形ABCD中,AB=4,E,F分别为边AB,BC的中点,连接AF,DE,点G,H分别为DE,AF的中点,连接GH,则GH的长为 .
19.如图,在矩形ABCD中,AB=3,AD=4,动点E从点B出发,以每秒3个单位长度的速度沿BC向右运动,同时动点F从点D出发,以每秒4个单位长度的速度沿DA向左运动,当点F到达点A时运动停止,连接EF,过点C作CG⊥EF于点G,则CG的最大值为 .
20.如图,在正方形ABCD中,,点E为边AD上一点,连接BE,点G在BE上,以GE为边作等边△EFG,点F落在CD上,M为GF中点,连接CM,则CM的最小值为 .
三、解答题
21.已知正方形ABCD,点E,F,G分别在边CD,BC,AD上,连接AE、GF,
(1)若AE⊥GF于点H.
①如图1,求证:AE=GF;
②如图2,将GF向下平移,当点G与D重合时,若E为CD的中点,连接HC,求的值;
(2)如图;若AB=6,AG=CF=1.5,且CE=2DE,请你求出∠AHG的度数.
22.我们不妨约定:对角线互相垂直的凸四边形叫做“理正四边形”.
(1)①在“平行四边形,矩形,菱形”中,一定是“理正四边形”的有 ;②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形“理正四边形”.(填“是”或“不是”或“有可能是”)
(2)如图1,四边形ABCD是面积为1的“理正四边形”,且AC﹣BD=3求AC:BD的值;
(3)如图2,在平面直角坐标系中第一象限内有动点E,且1≤OE≤2,四边形ABCD是“理正四边形”(点A在x轴负半轴上,点B在y轴负半轴上,点C在x轴正半轴上,点D在y轴正半轴上),在并且EA=EB=EC=ED=3,求AC:BD的取值范围.
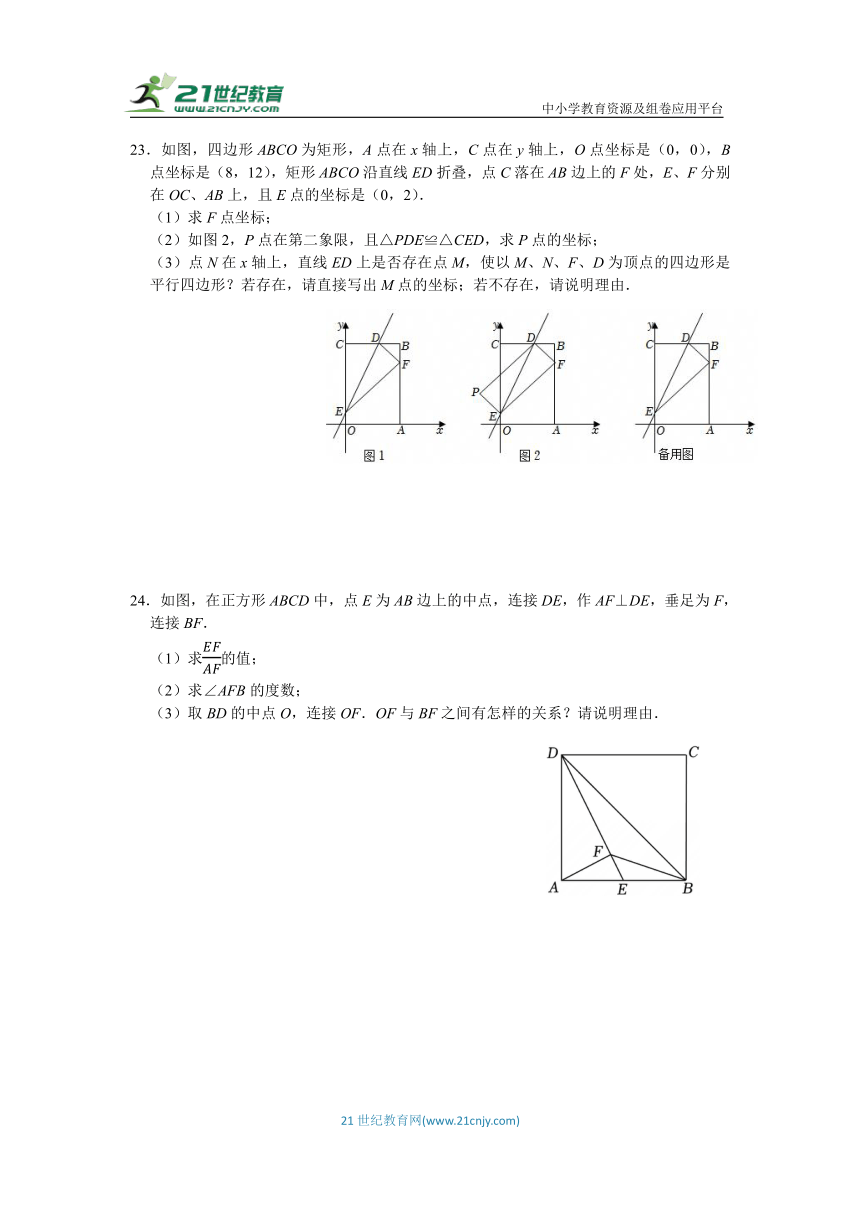
23.如图,四边形ABCO为矩形,A点在x轴上,C点在y轴上,O点坐标是(0,0),B点坐标是(8,12),矩形ABCO沿直线ED折叠,点C落在AB边上的F处,E、F分别在OC、AB上,且E点的坐标是(0,2).
(1)求F点坐标;
(2)如图2,P点在第二象限,且△PDE≌△CED,求P点的坐标;
(3)点N在x轴上,直线ED上是否存在点M,使以M、N、F、D为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
24.如图,在正方形ABCD中,点E为AB边上的中点,连接DE,作AF⊥DE,垂足为F,连接BF.
(1)求的值;
(2)求∠AFB的度数;
(3)取BD的中点O,连接OF.OF与BF之间有怎样的关系?请说明理由.
25.在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使C点恰好落在AD边上点F处,且AB≠BC.
(1)如图1,若BC=2BA,求∠CBE的度数;
(2)如图2,当DE=4,且AF FD=40时,求BC的长;
(3)如图3,作∠ABF的角平分线交AD于点N,若BC=5,,求AB的值.
26.如图,四边形ABCD为平行四边形,对角线AC的垂直平分线EF分别交边AD,BC于点E,F,垂足为O.
(1)求证:四边形AFCE为菱形;
(2)在BC的延长线上取一点G,使CG=OC,连接OG.若F为BC的中点,且∠G=15°,AB=8,求△FOG的面积.
27.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(6,8),点D为对角线OB的中点.点P是OC边上一动点,直线PD交AB边于点E.
(1)求证:四边形OPBE为平行四边形;
(2)若△ODP的面积与四边形OAED的面积之比为1:3,求点P的坐标;
(3)设点Q是x轴上方平面内的一点,以点O、D、P、Q为顶点的四边形是菱形,直接写出点Q的坐标.
28.如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE,连接CF、CE.
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,连接GE.求证:GE=BE+GD;
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题:
①如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB的中点,且∠DCE=45°,求DE的长;
②如图3,在菱形ABCD中,∠BAD=120°,E、F分别在BC和CD上,且∠EAF=60°,连接EF.若BE=2,DF=4,请直接写出EF的长度 .
29.如图1和图2,在 ABCD中,AB=15,BC=7,,连接对角线BD.点P是对角线BD上一点,作∠EPD=∠ABC,射线PE交射线BA于点E,设BP=x.
(1)如图1,点E在BA的延长线上,当PE=AD时,求证:△PBE≌△ABD;
(2)如图2,点E与点A重合时,求x的值;
(3)连接AP,当△APE是以AP为底的等腰三角形时,求x的值;
(4)点E在BA延长线上,连接DE,当∠ADE为锐角时,直接写出∠ADE的正切值(用含x的式子表示).
30.如图1,在矩形ABCD中,BD为对角线,BD的垂直平分线分别交AD,BD,BC于点E,O,F,连接BE,DF.
(1)求证:四边形BEDF是菱形.
(2)如图2,连接CO,若AE=2,AD=6,求cos∠BCO的值.
31.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=2,AD=4,求EC的长;
(3)若AE﹣DE=2EC,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A C B B A C D A
1.【解答】解:∵四边形ABCD是正方形,△ABP是等边三角形,
∴AB=BP=BC,∠ABC=90°,∠ABP=60°,
∴∠DAP=∠CBP=30°,
∴∠BCP=∠BPC=75°,故①正确;
∵AD=BC,AP=BP,∠DAP=∠CBP=30°,
∴△DAP≌△CBP(SAS),故②正确;
如图,∵△ABP是等边三角形,过点P作PG⊥AB于点G,PH⊥AD于点H,
∴AG=GB,
∵∠BAD=∠AGP=90°,
∴四边形AGPH是矩形,
∴PH=AG,
∵S△ABCBC×ABAD×AB,S△ADPAD×PHADABAD×AB,
∴△ADP和△ABC的面积比为1:2,故③正确;
∵∠PCD=∠BCD﹣∠BCP=15°,PC=PD,
∴∠PCD=∠PDC=15°,
∴∠CPN=30°,
∵CN⊥DP,
∴CNPC,
∴S△PDCDP×CNPC2,故④正确,
综上所述:①②③④.
故选:D.
2.【解答】解:由翻折变换可知,AD=AF,∠DAE=∠FAE,DE=FE,∠D=∠AFE,
∴∠AFG=180°﹣∠AFE=90°=∠B,
在Rt△ABG和Rt△AFG中,
,
∴Rt△ABG≌Rt△AFG(HL),因此①正确;
∴∠BAG=∠FAG,
又∵∠BAG+∠FAG+∠DAE+∠FAE=90°,
∴∠GAE=∠FAG+∠FAE90°=45°,因此②正确;
由翻折变换可知,DE=EF,
由全等三角形可知BG=GF,
设正方形的边长为a,BG=x,DE=EFa,则CG=a﹣x,GE=xa,EC=aaa,
在Rt△ECG中,由勾股定理得,
EC2+GC2=EG2,
即(a)2+(a﹣x)2=(xa)2,
解得xa,
即BGaBC,
∴BG=CG,因此③正确;
∴BG=CG=FG,
∴∠GCF=∠GFC,
由三角形全等可得,∠AGB=∠AGF,
又∵∠AGB+∠AGF+∠FGC=180°=∠FGC+∠GCF+∠GFC,
∴∠ABG=∠FCG,
∴AG∥FC,因此④正确,
∵BG=CG,
∴BGAB,
∴tan∠AGB=2,
∴∠AGB≠60°,
∵AG∥CF,
∴∠FCG=∠AGB≠60°,
∴△GCF不是等边三角形,因此⑤不正确;
故选:C.
3.【解答】解:∵正方形ABCD的边长为12,
∴AD=CD=12,∠ADF=∠CDF=45°.
∵DF=DF,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAE=∠FCD.
∵E为CD的中点,
∴.
∴.
故选:A.
4.【解答】解:∵点E在正方形ABCD内部,且△ABE是等边三角形,BD是正方形的对角线,
∴∠ADB=45°,∠DAE=90°﹣60°=30°,AD=AE,
∴∠BDE(180°﹣∠DAE)(180°﹣30°)=75°,
∴∠BDE=∠ADE﹣∠ADB=75°﹣45°=30°,
故选:C.
5.【解答】解:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠A=∠B=∠BCD=90°,
在△CBF和△DCE中,
,
∴△CBF≌△DCE(SAS),
∴∠BCF=∠CDE,
∵∠BCD=∠BCF+∠DCF=90°,
∴∠CDE+∠DCF=90°,
∴∠DMC=180°﹣(∠CDE+∠DCF)=90°,
∴△DMF为直角三角形,
∵点N为DF的中点,
∴MNDF,
∵AF=1,CE=BF=2,
∴AB=AF+BF=3,
在Rt△ADF中,AD=AB=3,AF=1,
由勾股定理得:DF,
∴MNDF.
故选:B.
6.【解答】解:连接CB,
根据三角形的外角等于和它不相邻的两个内角之和可得,∠M+∠N=∠3,∠H+∠G=∠4,∠3=∠1+∠KEF,∠4=∠2+∠KEF,
∴∠M+∠N+∠H+∠G=∠3+∠4=∠1+∠2+2∠KEF=180°+120°=300°,
∵∠KEF=120°,
∴∠FEC=∠5+∠6=180°﹣∠KEF=180°﹣120°=60°,
∵∠A+∠D+∠7+∠5+∠6+∠8=360°,
∴∠A+∠D+∠7+∠8=360°﹣60°=300°,
∴∠A+∠ABE+∠ECD+∠D+∠H+∠G+∠M+∠N=600°.
故选:B.
7.【解答】解:延长CE交AB于点H,过点E作EM⊥AB于点M,ME的延长线交CD于点N,过点F作FP⊥BC于点P,如图所示:
∵四边形ABCD是正方形,
∵AB=BC=CD=AD,AB∥CD,∠ABC=∠BCD=90°,
∴△BEH∽△DEC,
∴,
∵DE=2BE,
∴,
∴BHCDAB,HECE,
设BH=a,则AB=2a,
∴AB=BC=CD=AD=2a,
在Rt△BCH中,由勾股定理得:CH,
∵HECE,
∴HECH,CECH,
∵MN⊥AB,
∴∠BMN=∠MNC=∠ABC=90°,
∴四边形MNCB是矩形,
∴MN=BC=2a,EN⊥CD,
∵AB∥CD,
∴△BEM∽△DEN,
∴,
∴EMEN,
∴EMMN,ENMN,
∵DF⊥CE,
∴由三角形的面积公式得:S△BECCE DFCD EN,
∴CE DF=CD EN,
∴,
∴DF,
在Rt△DCF中,由勾股定理得:CF,
∵FP⊥CD,DF⊥CE,
∴∠CPF=∠DFC=90°,
∴∠PCF+∠CFP=90°,
∵∠PCF+∠DCF=∠BCD=90°,
∴∠CFP=∠DCF,
∴△CFP∽△DCF,
∴,
∴,
∴FP,PC,
∴BP=BC﹣PC,
在Rt△BFP中,由勾股定理得:BF,
∴ .
故选:A.
8.【解答】解:∵四边形DECF是正方形,
∴DE=DF,DE∥AC,∠DEB=∠AFD=90°,
∴∠BDE=∠A,
∴△BDE∽△DAF,
∴,设DE=3k,AF=5k,
在Rt△ADF中,则有25=9k2+25k2,
∴k2,
∴S△ADF 3k 5k,
∵,
∴S△BDE,
∴S△ADF+S△BDE7.5,
故选:C.
9.【解答】解:连接AG,
∵E、F分别为AH、GH的中点,
∴EFAG,
∴当AG最小时,EF最小,当AG⊥BC时,AG最小,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=120°,
∴∠B=60°,
∴当AG⊥BC时,∠AGB=90°,
∴sinB=sin60°,
∴AG=4,
∴EF的最小值42.
故选:D.
10.【解答】解:设③的边长为a,④的边长为b,②的宽为x,
∴⑤的边长为a+b,②的长为:a+a+b=2a+b,①的长为x+a,宽为b﹣a,
∴②的周长为:2(2a+b+x)=4a+2b+2x,
∵①的周长=2(x+a+b﹣a)=2x+2b,③的周长为4a,
∴①与③的周长和为:4a+2b+2x,
∴甲的说法正确;
∵①的周长=2(x+a+b﹣a)=2x+2b,⑤的周长为2(a+b)=2a+2b,
∴①与⑤的周长和为:2a+2b+2x+2b=2a+4b+2x,
∴乙的说法错误;
∵③的周长=4a,④的周长=4b,
∴③与④的周长和为:4a+4b,
∴丙的说法错误;
∵⑤的周长为2(a+b)=2a+2b,①的周长=2(x+a+b﹣a)=2x+2b,
∴⑤与①的周长差为:2a+2b﹣2x﹣2b=2a﹣2x,
∴丁的说法错误;
综上可知:说法正确的只有甲,
故选:A.
二、填空题
11.【解答】解:连接AP,如图1所示:
∵在Rt△ABC中,∠BAC=90°,PE⊥AB,PF⊥AC,
∴四边形AEPF是矩形,
∴EF=AP,
∵点P为斜边BC上的一个动点,
∴线段EF的最小值为线段AP的最小值,由点P到直线BC的距离中垂线段最短,过A作AP⊥BC,如图2所示:
在Rt△ABC中,∠BAC=90°,AB=3,AC=4,则由勾股定理可得,
∴由等面积法可得,即3×4=5AP,解得,
故答案为:.
12.【解答】解:如图,
∵四边形ABCD是正方形,
∴BC=CD,∠BCE=∠CDF=90°,
∵CE=DF,
∴△BCE≌△CDF(SAS),
∴∠EBC=∠FCD,
∵∠FCD+∠BCG=90°,
∴∠CBE+∠BCG=90°,
∴∠CGB=90°,
∴点G的运动轨迹是以BC为直径的⊙O,
当O,G,D共线时,DG的值最小,最小值,
故答案为.
13.【解答】解:连接AC,过A作AM⊥BC于M,在BC上截取BK=BE,连接GK,
∵四边形ABCD是菱形,
∴∠ABC=∠CBD,BC=BA,BC∥AD,
∵BG=BG,
∴△BGK≌△BGE(SAS),
∴GK=GE,∠BEG=∠BKG,
∵GF+GE=3,
∴GF+GK=3,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AMAB23,
∴GF+GK=AM,
∴F、G、K共线,且FK⊥BC,
∴∠BEG=∠BKG=90°,
∵AD∥BC,
∴FK⊥AD,
∴∠GFD=90°,
∵四边形ABCD是菱形,
∴∠GBE=∠GDF∠ABC=30°,AB=AD=2,
∴BEGE,DFGF,
∴BE+DF(GE+GF)=3,
∴AE+AF=BA+AD﹣(BE+DF)=223.
故答案为:.
14.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
15.【解答】解:因为点D(5,3)在边AB上,四边形OABC是正方形,
所以AB=BC=5,BD=5﹣3=2;
(1)若以C为中心,把△CDB顺时针旋转90°,
则点D′在x轴上,OD′=2,
所以D′(﹣2,0);
(2)若以C为中心,把△CDB逆时针旋转90°,
则点D′到x轴的距离为10,到y轴的距离为2,
所以D′(2,10),
综上,旋转后点D的对应点D′的坐标为(﹣2,0)或(2,10).
故答案为:(﹣2,0)或(2,10).
16.【解答】解:由题意可得:AB=CD=4,AD=BC=6,AD∥BC,
∴,
∴△EFG∽△DAG,
∴,
∴,
过点G作GH⊥BC于点H,
∴GH∥CD,EC=EF+FC=4,
∴△EHG∽△ECD,
∴,
∴,,
∴BH=BE+EH=2+1=3,且∠EHG=90°,
∴,
∴,
故答案为:.
17.【解答】解:①过点G作GP⊥AD于P,GQ⊥CD于Q,如图,
∵正方形ABCD,
∴∠ADC=90°,DB平分∠ADC,
∵GP⊥AD,GQ⊥CD,
∴GP=GQ,∠GPD=∠GQD=90°,
∴∠PGQ=90°,即∠FGQ+∠FGP=90°,
∵AG⊥GF,
∴∠FGP+∠PGA=∠FGA=90°,
∴∠FGP=∠PGA,
∴△FGQ≌△AGP(ASA),
∴AG=FG,故①正确;
②∵AG=FG,∠FGA=90°,
∴∠GAF=∠GFA=45°,
∵∠BAD=90°,
∴∠BAG+∠DAF=45°,
将△ABG绕点A逆时针旋转90度,得到△ADM,
则AM=AG,DM=BG,∠DAM=∠BAG,∠ADM=∠ABG=45°,
∴∠HDM=∠HDA+∠ADM=45°+45°=90°,
∴DM2+DH2=HM2,
∴∠HAM=∠HAD+∠DAM=∠HAD+∠BAG=45°=∠GAH,
∵AH=AH,
∴△AMH≌△AGH(SAS),
∴GH=HM,
∴BG2+DH2=GH2,故②正确;
③∵,
∴,
∴,
∴,
∴∠DHM=30°,
∴∠GHM=180°﹣∠DHM=150°;
∵△AMH≌△AGH,
∴,
∴∠BGE=∠AGH=180°﹣∠GAH﹣∠GHA=180°﹣45°﹣75°=60°,故③正确;
④将△ABE绕点A逆时针旋转90度,得到△ADN,连接EF,
则DN=BE,AN=AE,
同理可得△AEF≌△ANF,
∴EF=FN=FD+DN=FD+BE,∠AFE=∠AFN,
由∠AHG=75°,
∴∠FHD=75°,
∵∠FDH=45°,
∴∠AFD=180°﹣∠FHD﹣∠FDH=60°,
∴∠AFE=∠AFN=60°,
∴∠EFC=180°﹣∠AFD﹣∠AFE=60°,
∴∠CEF=30°,
∴,
由勾股定理,得EF2=CE2+CF2,
即,
∴,
∴,故④错误;
∴正确有①②③.
故答案为:①②③.
18.【解答】解:连接AG并延长AG交CD于点P,连接PF,如图所示,
∵四边形ABCD是正方形,
∴CD=BC=AB=4,∠C=90°,AB∥CD,
∴∠AEG=∠GDP,
∵E、F分别为边AB、BC的中点,
∴AEAB=2,CFBC=2.
∵G为DE的中点,
∴EG=DG,
在△EAG和△DPG中,
,
∴△EAG≌△DPG(ASA).
∴AG=PG,DP=AE=2.
∴G为AP的中点,
∵H为AF的中点,
∴GH是△APF的中位线.
∴GHPF.
在Rt△FCP中,
CP=DC﹣DP=4﹣2=2,
∴PF2.
∴GHPF.
故答案为:.
19.【解答】解:如图,在AD,BC上截取线段AM,BN,使得AM=BN,连接MN交EF于点K.连接CK,CK的中点为O.
∵四边形ABCD是矩形,
∴AD=BC=4,AD∥BC,∠A=90°,
∵AM=BN,
∴四边形ABNM是平行四边形,
∵∠A=90°,
∴四边形ABNM是矩形,
∴∠AMN=∠MNB=90°,AB=MN=3,
∵FM∥EN,
∴△MKF∽△NKE,
∴,
∴KNMN3,
∵∠CNK=90°,CN=4,
∴CK,
∵CG⊥EF,
∴∠CGK=90°,
∵OK=OC,
∴OG=OK=OC=ON,
∴点G在⊙O上运动,
∴CG的最大值=CK.
故答案为:.
20.【解答】解:∵正方形ABCD,
∴,
作∠CDN=30°,
∵以GE为边作等边△EFG,点F落在CD上,M 为GF中点,
∴EM⊥GF,
∴∠EMF=90°,,
∵四边形ABCD是正方形,
∴∠EDF=90°,
∴点E、D、F、M四点共圆,所以∠MDF=∠MEF=30°,
∴当点E在AD上运动时,点M在DN上运动,当CM⊥DN时,CM最小,
∵∠CDN=30°,
∴CM最小值,
故答案为:.
三、解答题
21.【解答】(1)①证明:过G作GM⊥BC于M,
∵正方形ABCD,
∴AB=BC=CD=DA,∠D=∠C=∠GMC=90°,
∴四边形MGDC是矩形,
∴AD=DC=GM,∠ADE=∠GMF=∠AGM=90°,
∵GH⊥AE,
∴∠MGF=90°﹣∠AGF=∠DAE,
∵
∴△ADE≌△GMF(ASA),
∴AE=GF.
②过点H作HM⊥DC于点M,
∵E为CD的中点,不妨设DE=EC=x
∵正方形ABCD,
∴AD=DC=2x,∠ADC=90°,
∴,
∵DF⊥AE于点H,
∴,
∴,,
∴,
∴,
∴,
∴,
∴.
(2)如图,以点D为原点,以DC所在直线为x轴建立平面直角坐标系,
∵AB=6,AG=CF=1.5,且CE=2DE,
∴CE=4,DE=2,
∴A(0,6),E(2,0),,
设直线AE的解析式为y=kx+b,
根据题意,得,
解得,
∴直线AE的解析式为y=﹣3x+6;
设直线GF的解析式为y=px+q,
根据题意,得,
解得,
∴直线GF的解析式为;
由此得,
解得,
故点,
∴,
设直线GF与x轴的交点为P,
∴点P(9,0),
∴PE=9﹣2=7,,
∴,
过点E作EQ⊥GF于点Q,
∴,
∴,
∴HQ=EQ,
∴∠EHQ=45°,
∴∠AHG=45°.
22.【解答】解:(1)①∵菱形的对角线互相垂直,
∴菱形是“理正四边形”,
∵平行四边形、矩形的对角线不一定垂直,
∴不一定是“理正四边形”,
故答案为:菱形;
②若四边形ABCD是“理正四边形”,则AC⊥BD,
∵AB=AD,
∴OB=OD,
∴AC是BD的垂直平分线,
∴CB=CD,
又∵CB≠CD,
∴四边形ABCD不是“理正四边形”.
故答案为:不是;
(2)∵四边形ABCD是面积为1的“理正四边形”,
∴,
∴BD AC=2,
∵AC﹣BD=3,
∴(AC+BD)2=(AC﹣BD)2+4AC BD=32+4×2=17,
∴,
联立,
解得,
∴;
(3)如图,过E作EM⊥BD于M,EN⊥AC于N,
∵EM⊥BD,EN⊥AC,
∴∠MON=∠OME=∠ONE=90°,
∴四边形OMEN是矩形,
∴OM=NE,ME=ON,
设ME=ON=m,OM=NE=n,
∵EA=EB=EC=ED=3,
在Rt△DME中,ME2+MD2=DE2,
∴,
在Rt△NEC中,NE2+NC2=CE2,
∴,
∴,
整理得,
解得:,
∴,
在Rt△MEO中,ME2+MO2=OE2,
∴m2+n2=OE2,
∵1≤OE≤2,
∴1≤OE2≤4,
∴1≤m2+n2≤4,
∵E是第一象限内的动点,
∴m>0,n>0,
∴0<m2<4,
∴9﹣m2>0,
∵1≤m2+n2≤4,
1﹣m2≤n2≤4﹣m2,
∴m2﹣4≤﹣n2≤m2﹣1,
∴m2+5≤9﹣n2≤m2+8,
∴,
∴,
∴,
∴,
∵0<m2<4,
∴当m2=4时,,
当m2=0时,,
∴,
∴.
23.【解答】解:(1)如图1,作EG⊥AB于点G,则EG∥x轴,
∵四边形ABCO为矩形,A点在x轴上,C点在y轴上,O(0,0),E(0,2),B(8,12),
∴G(8,2),C(0,12),
由折叠得EF=CE=12﹣2=10,
∵∠EGF=90°,EG=8,
∴FG6,
∴AF=AG+FG=2+6=8,
∴F(8,8).
(2)如图2,作PH⊥y轴于点H,
∵△PDE≌△CED,
∴DP=EC,∠PDE=∠CED,
∵EC=EF,∠CED=∠FED,
∴DP=EF,∠PDE=∠FED,
∴DP∥EF,
∴四边形PDFE是平行四边形,
∵∠DPE=∠ECD=90°,
∴四边形PDFE是矩形,
∴∠PEF=∠EFD=90°,
∴∠HEP+∠CEF=90°,∠BFD+∠AFE=90°,
∵AB∥OC,
∴∠CEF=∠AFE,
∴∠HEP=∠BFD,
∵∠PHE=∠DBF=90°,PE=DF,
∴△PHE≌△DBF(AAS),
∵AB=12,AF=8,BC=8,
∴BF=AB﹣AF=12﹣8=4,DF=DC=8﹣BD,
∵∠B=90°,
∴BF2+BD2=DF2,
∴42+BD2=(8﹣BD)2,
∴BD=3,
∴HP=BD=3,HE=BF=4,DF=DC=8﹣3=5,
∴OH=2+4=6,
∴P(﹣3,6).
(3)存在,设直线DE交x轴于点L,
如图3,四边形FDMN是平行四边形,且点M在线段DE上,
作MQ⊥x轴于点Q,则∠MQN=∠FBD=90°,
∵FN∥DM,BC∥OA,
∴∠ANF=∠ALD=∠CDE,
∴∠FNM=∠MDF,
∴180°﹣∠ANF﹣∠FNM=180°﹣∠CDE﹣∠MDF,
∴∠MNQ=∠FDB,
∵MN=FD,
∴△MNQ≌△FDB(AAS),
∴QM=BF=4,
设M(x,4),设直线DE的解析式为y=kx+2,
∵D(5,12),
∴5k+2=12,
解得k=2,
∴直线DE的解析式为y=2x+2,
把M(x,4)代入y=2x+2得2x+2=4,
解得x=1,
∴M(1,4);
如图4,四边形FDMN是平行四边形,且点M在DE的延长线上,
作MR⊥x轴于点R,则∠MRN=∠FBD=90°,作CW∥DF交x轴于点W,
∵MN∥DF,
∴CW∥DF,
∴∠MNR=∠OWC=∠WCB=∠FDB,
∵MN=FD,
∴△MNR≌△FDB(AAS),
∴RM=BF=4,
设M(x,﹣4),
把M(x,﹣4)代入y=2x+2得2x+2=﹣4,
解得x=﹣3,
∴M(﹣3,﹣4);
如图5,四边形FDMN是平行四边形,且点M在ED的延长线上,
作MT⊥CD交CB的延长线于点T,则∠T=∠FAN=90°,
∵FN∥DM,
∴∠MDT=∠MLA=∠FNA,
∵MD=FN,
∴△MDT≌△FNA(AAS),
∴TM=AF=8,
∴yM=12+8=20,
设M(x,20),
把M(x,20)代入y=2x+2得2x+2=20,
解得x=9,
∴M(9,20),
综上所述,点M的坐标为(1,4)或(﹣3,﹣4)或(9,20).
24.【解答】解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠BAD=∠EAF+∠DAF=90°,
∵AF⊥DE,
∴∠AFD=∠AFE=90°,
∴∠ADF+∠DAF=90°
∴∠EAF=∠ADE,
∵E是AB的中点,
∴,
∴,
在Rt△AEF中,,
∴,
在Rt△ADE中,;
(2)∵BD是正方形ABCD的对角线,
∴
由(1)得∠AFE=90°,
∴,
同理,得,
∴,
又∵AE=BE,
∴,
又∵∠BEF=∠DEB,
∴△BEF∽△DEB,
∴∠BFE=∠DBE=45°.
∴∠AFB=90°+45°=135°;
(3)OF⊥FB且 FB=2OF,
理由如下:
由(2)得△BEF∽△DEB,
∴,
∵O是BD的中点,
∴,
∵,∠AFE=90°,
∴,
∴,
即,
在△ABF中,∠BAF=180°﹣∠AFB﹣∠ABF=45°﹣∠ABF,
而∠DBF=45°﹣∠ABF,
∴∠EAF=∠OBF,
∴△BFO~△AFE,
∴,∠BFO=∠AFE=90°,
∴BF=2OF,BF⊥OF.
25.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=∠C=90°,
∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
∴BC=BF,∠FBE=∠EBC,∠C=∠BFE=90°,
∵BC=2BA,
∴BF=2BA,
∴∠AFB=30°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFB=∠CBF=30°,
∴∠CBE∠CBF=15°;
(2)∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
∴∠BFE=∠C=90°,CE=EF,
在矩形ABCD中,∠A=∠D=90°,AB=CD,
∴∠AFB+∠DFE=90°,∠DEF+∠DFE=90°,
∴∠AFB=∠DEF,
∴△FAB∽△EDF,
∴,
∴AF DF=AB DE,
∵DE=4,AF FD=40,
∴AB=10=CD,
∴CE=CD﹣DE=10﹣4=6,
∴EF=6,
∴DF2,
∴AF4,
∴BC=AD=AF+DF=6;
(3)如图3,过点N作NG⊥BF于点G,
∵∠NFG=∠AFB,∠NGF=∠BAF=90°,
∴△NFG∽△BFA,
∴,
∵BC=BF=5,NF,
∴,
∴NGAB,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG,
又∵BN=BN,
∴Rt△ABN≌Rt△GBN(HL),
∴AB=BG,
∴FG=BF﹣BG=5﹣AB,
在Rt△NGF中,NG2+FG2=NF2,
∴(AB)2+(5﹣AB)2=()2,
∴AB=4或AB=5(舍去),
∴AB的值为4.
26.【解答】(1)证明:∵EF垂直平分AC,
∴EF⊥AC,AO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OCF=∠OAE,
在△AOE 与△COF中,
,
∴△AOE≌△COF(AAS),
∴FO=EO,
又∵CO=AO,
∴四边形AFCE是平行四边形,
又∵EF⊥AC,
∴平行四边形AFCE为菱形;
(2)解:∵OC=CG,
∴∠COG=∠G=15°,
∴∠ACB=∠COG+∠G=30°,
∵四边形AFCE为菱形,
∴O为AC的中点,
∵F为线段BC的中点,
∴OF是三角形ABC的中位线,
∴,
∵EF⊥AC,
∴,,
∴,,
如图,作 OH⊥BC,垂足为H,则∠OHG=90°,
∴,
则.
27.【解答】(1)证明:∵四边形形OABC是矩形,
∴OC∥AB,
∴∠COB=∠OBA,∠OPE=∠PEB,
∵D为OB中点,
∴OD=BD,
∴△OPD≌△BED(AAS),
∴OP=BE,
又∵OC∥AB,即OP∥BE,
∴四边形OPBE为平行四边形;
(2)解:∵O(0,0),B(6,8),
∴OB中点D坐标为(3,4),
设P(0,t),则OP=t,
∴S△OPDt 3,
设PD的直线表达式为y=kx+t,
∵D在PD上,
∴4=3k+t,
∴k,
∴PD:y.
令x=6,则y=﹣t+8,
∴E(6,8﹣t).
∴S四边形OAED=S△AED+S△ODA(8﹣t)+1224.
∵S△OPD:S四边形OAED=1:3,
∴24=3,
解得:t=4,
∴P(0,4).
(3)解:Q的坐标为(3,9)或(﹣3,4)或(3,).
如图,以OD为边,四边形ODQP为菱形,
∵D(3,4),
∴OD5,
∴Q(3,9);
如图,以OD为边,四边形ODPQ为菱形,
∴点D与点Q关于y轴对称,
∴Q(﹣3,4);
如图,以OD为对角线,四边形OQDP为菱形,延长DQ交x轴于点H,则QH⊥x轴,
设OQ=DQ=m,则QH=4﹣m,
∴32+(4﹣m)2=m2,
∴m,
∴DQ,
∴QH=4,
∴Q(3,).
综上所述,Q的坐标为(3,9)或(﹣3,4)或(3,).
28.【解答】(1)证明:在正方形ABCD中 CB=CD,∠B=∠CDA=90°,
∴∠CDF=∠B=90°.
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS).
∴CE=CF;
(2)证明:GE=BE+GD成立.理由如下:
∵∠BCD=90°,∠GCE=45°,
∴∠BCE+∠GCD=45°.
∵△BCE≌△DCF(已证),
∴∠BCE=∠DCF.
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=45°.
∴∠ECG=∠FCG=45°.
在△ECG和△FCG中,
,
∴△ECG≌△FCG(SAS).
∴GE=FG.
∵FG=GD+DF,
∴GE=BE+GD;
(3)①如图2,过点C作CG⊥AD,交AD的延长线于点G,
由(2)和题设知:DE=DG+BE,
设DG=x,则AD=6﹣x,DE=x+3,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(6﹣x)2+32=(x+3)2,
解得x=2.
∴DE=2+3=5;
②把△ABE旋转120°得到△ADE′,则DE′=BE=2,DF=4,EF=E′F,∠ADE′=∠B=60°,
∴∠E′DF=120°,
过E′作E′H⊥FD于H,∠E′DH=60°,
∴DHDE′=1,HE′DE′,
∴EF2.
故答案为:2.
29.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠ADB=∠DBC,
∵∠EPD=∠ABC,∠EBP+∠BEP=∠EPD,∠EBP+∠DBC=∠ABC,
∴∠BEP=∠DBC,
∴∠BEP=∠ADB,
在△PBE和△ABD中,
∴△PBE≌△ABD(AAS);
(2)解:过点D作DF⊥BC,交BC的延长线于点F,如图,
∵AB∥CD,
∴∠DCF=∠ABC,,
∴DF=CD sin∠DCF=12,
∴,
∴BF=BC+CF=16,
∴,
由(1)得∠BEP=∠ADB,∠PBE=∠ABD,
∴△PBE△ABD,
∴,
∵AB=BE,
∴;
(3)解:△APE是以AP为底的等腰三角形,即AE=PE,
①当点E在线段AB上时,如图,
∵△PBE∽△ABD,
∴,
∵BE=AB﹣AE=AB﹣PE,
∴,
解得,
∴;
②当点E在BA延长线上时,如图,
∵△PBE∽△ABD,
∴,
∵BE=AB+AE=AB+PE,
∴,
解得,
∴.
综上所述,x的值为或;
(4)解:∠ADE的正切值为.
过E作EF⊥AD于点F,
由(2)知△PBE△ABD,
∴,
∴,
∴BE,
∴AE=BE﹣AB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ABC=∠DAE,
∴sin∠ABC=sin∠DAE,
∴EF=AE sin∠DAE=(),
∴AF,
∴DF=7﹣()=16,
∴tan∠ADE.
30.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,
∴∠EDO=∠FBO,DE∥BF,
∵EF是BD的垂直平分线,
∴OB=OD,BE=DE,
∴∠BDF=∠DBF,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA),
∴DE=BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∵EF是BD的垂直平分线,
∴BE=DE=AD﹣AE=6﹣2=4,
∴AB2,
∴BD4
∵OB=OD,∠BCD=90°,
∴OB=OC,
∴∠BCO=∠CBD=∠ADB,
∴cos∠BCO=cos∠ADB.
31.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由翻折可知,∠D=∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠CEF=90°,
∴∠AFB=∠FEC,
∴△ABF∽△FCE.
(2)设EC=x,
由翻折可知,AD=AF=4,
∴BF2,
∴CF=BC﹣BF=2,
∵△ABF∽△FCE,
∴,
∴,
∴x,
∴EC.
(3)∵△ABF∽△FCE,
∴,
∴tanα+tanβ,
设AB=CD=a,BC=AD=b,DE=x,
∴AE=DE+2CE=x+2(a﹣x)=2a﹣x,
∵AD=AF=b,DE=EF=x,∠B=∠C=∠D=90°,
∴BF,CF,
∵AD2+DE2=AE2,
∴b2+x2=(2a﹣x)2,
∴a2﹣axb2,
∵△ABF∽△FCE,
∴,
∴,
∴a2﹣ax ,
∴b2 ,
整理得,16a4﹣24a2b2+9b4=0,
∴(4a2﹣3b2)2=0,
∴,
∴tanα+tanβ.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练四边形有关的综合问题
一、选择题
1.如图,在正方形ABCD中,以AB为边作等边三角形ABP,连接AC,PD,PC,则下列结论;①∠BCP=75°;②△ADP≌△BCP;③△ADP和△ABC的面积比为1:2;④.其中结论正确的序号有( )
A.①②④ B.②③ C.①③④ D.①②③④
2.如图,正方形ABCD中,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE.延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠GAE=45°;③BG=GC;④AG∥CF;⑤△GCF是等边三角形,其中正确结论有( )个.
A.2 B.3 C.4 D.5
3.如图,正方形ABCD的边长为12,E为CD的中点,连接BD,AE交于点F,连接CF,则tan∠FCD的值为( )
A. B. C. D.
4.如图,点E在正方形ABCD的内部,且△ABE是等边三角形,连接BD,DE,则∠BDE=( )
A.37.5° B.35° C.30° D.25°
5.2024年6月2日6时23分,嫦娥六号着陆器和上升器组合体在鹊桥二号中继星的支持下,成功着陆在月球背面南极一艾特肯盆地预选着陆区.组合体元件中有个展板的平面图如图所示,在正方形ABCD中,E,F分别是BC,AB上的点,DE,CF相交于点M.N是DF的中点,若AF=1,CE=BF=2,则MN的长为( )
A. B. C.2 D.
6.如图所示,已知∠KEF=120°,则∠A+∠B+∠C+∠D+∠H+∠G+∠M+∠N=( )
A.540° B.600° C.620° D.720°
7.如图,正方形ABCD的对角线BD上有一点E,满足DE=2BE,连接CE,过D作DF⊥CE 于F,连接BF.则的值为( )
A. B. C. D.
8.如图,正方形CEDF的顶点D,E,F分别在△ABC的边AB,BC,AC上.AD=5,DB=3,则△AFD与△BDE面积之和等于( )
A.5.5 B.6 C.7.5 D.8
9.如图,在 ABCD中,∠C=120°,AB=8,AD>AB,H、G分别是CD、BC上的动点,连接AH、GH,E、F分别为AH、GH的中点,则EF的最小值是( )
A.4 B.5 C. D.
10.如图,在一个大长方形中放入了标号为①,②,③,④,⑤五个四边形,其中①,②为两个长方形,③,④,⑤为三个正方形,相邻图形之间互不重叠也无缝隙.若想求得长方形②的周长,甲、乙、丙、丁四位同学提出了自己的想法:
甲说:只需要知道①与③的周长和;乙说:只需要知道①与⑤的周长和;
丙说:只需要知道③与④的周长和;丁说:只需要知道⑤与①的周长差.
下列说法正确的是( )
A.只有甲正确 B.甲和乙均正确
C.乙和丙均正确 D.只有丁正确
二、填空题
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为斜边BC上的一个动点,过P分别作PE⊥AB于点E,作PF⊥AC于点F,连接EF,则线段EF的最小值为 .
12.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为 .
13.如图,已知菱形ABCD的边长为2°,点G、E、F分别是BD、AB、AD上的点,若GE+GF=3,则AE+AF的值是 .
14.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
15.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D 的坐标是 .
16.如图,在矩形ABCD中,E,F是边BC上两点,且BE=EF=FC,连接DE,AF,DE与AF相交于点G,连接BG.若AB=4,BC=6,则cos∠GBF的值为 .
17.如图,在正方形ABCD中,点E、F分别是边BC、CD上的两个点,连接AE、AF分别与对角线BD交于点G、H,连接GF,若AG⊥GF,DHBG,下列说法正确的序号是 .
①AG=FG;②BG2+DH2=GH2;③∠BGE=60°;④若CE=3,BE+DF值为3.
18.如图,在正方形ABCD中,AB=4,E,F分别为边AB,BC的中点,连接AF,DE,点G,H分别为DE,AF的中点,连接GH,则GH的长为 .
19.如图,在矩形ABCD中,AB=3,AD=4,动点E从点B出发,以每秒3个单位长度的速度沿BC向右运动,同时动点F从点D出发,以每秒4个单位长度的速度沿DA向左运动,当点F到达点A时运动停止,连接EF,过点C作CG⊥EF于点G,则CG的最大值为 .
20.如图,在正方形ABCD中,,点E为边AD上一点,连接BE,点G在BE上,以GE为边作等边△EFG,点F落在CD上,M为GF中点,连接CM,则CM的最小值为 .
三、解答题
21.已知正方形ABCD,点E,F,G分别在边CD,BC,AD上,连接AE、GF,
(1)若AE⊥GF于点H.
①如图1,求证:AE=GF;
②如图2,将GF向下平移,当点G与D重合时,若E为CD的中点,连接HC,求的值;
(2)如图;若AB=6,AG=CF=1.5,且CE=2DE,请你求出∠AHG的度数.
22.我们不妨约定:对角线互相垂直的凸四边形叫做“理正四边形”.
(1)①在“平行四边形,矩形,菱形”中,一定是“理正四边形”的有 ;②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形“理正四边形”.(填“是”或“不是”或“有可能是”)
(2)如图1,四边形ABCD是面积为1的“理正四边形”,且AC﹣BD=3求AC:BD的值;
(3)如图2,在平面直角坐标系中第一象限内有动点E,且1≤OE≤2,四边形ABCD是“理正四边形”(点A在x轴负半轴上,点B在y轴负半轴上,点C在x轴正半轴上,点D在y轴正半轴上),在并且EA=EB=EC=ED=3,求AC:BD的取值范围.
23.如图,四边形ABCO为矩形,A点在x轴上,C点在y轴上,O点坐标是(0,0),B点坐标是(8,12),矩形ABCO沿直线ED折叠,点C落在AB边上的F处,E、F分别在OC、AB上,且E点的坐标是(0,2).
(1)求F点坐标;
(2)如图2,P点在第二象限,且△PDE≌△CED,求P点的坐标;
(3)点N在x轴上,直线ED上是否存在点M,使以M、N、F、D为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
24.如图,在正方形ABCD中,点E为AB边上的中点,连接DE,作AF⊥DE,垂足为F,连接BF.
(1)求的值;
(2)求∠AFB的度数;
(3)取BD的中点O,连接OF.OF与BF之间有怎样的关系?请说明理由.
25.在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使C点恰好落在AD边上点F处,且AB≠BC.
(1)如图1,若BC=2BA,求∠CBE的度数;
(2)如图2,当DE=4,且AF FD=40时,求BC的长;
(3)如图3,作∠ABF的角平分线交AD于点N,若BC=5,,求AB的值.
26.如图,四边形ABCD为平行四边形,对角线AC的垂直平分线EF分别交边AD,BC于点E,F,垂足为O.
(1)求证:四边形AFCE为菱形;
(2)在BC的延长线上取一点G,使CG=OC,连接OG.若F为BC的中点,且∠G=15°,AB=8,求△FOG的面积.
27.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(6,8),点D为对角线OB的中点.点P是OC边上一动点,直线PD交AB边于点E.
(1)求证:四边形OPBE为平行四边形;
(2)若△ODP的面积与四边形OAED的面积之比为1:3,求点P的坐标;
(3)设点Q是x轴上方平面内的一点,以点O、D、P、Q为顶点的四边形是菱形,直接写出点Q的坐标.
28.如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE,连接CF、CE.
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,连接GE.求证:GE=BE+GD;
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题:
①如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB的中点,且∠DCE=45°,求DE的长;
②如图3,在菱形ABCD中,∠BAD=120°,E、F分别在BC和CD上,且∠EAF=60°,连接EF.若BE=2,DF=4,请直接写出EF的长度 .
29.如图1和图2,在 ABCD中,AB=15,BC=7,,连接对角线BD.点P是对角线BD上一点,作∠EPD=∠ABC,射线PE交射线BA于点E,设BP=x.
(1)如图1,点E在BA的延长线上,当PE=AD时,求证:△PBE≌△ABD;
(2)如图2,点E与点A重合时,求x的值;
(3)连接AP,当△APE是以AP为底的等腰三角形时,求x的值;
(4)点E在BA延长线上,连接DE,当∠ADE为锐角时,直接写出∠ADE的正切值(用含x的式子表示).
30.如图1,在矩形ABCD中,BD为对角线,BD的垂直平分线分别交AD,BD,BC于点E,O,F,连接BE,DF.
(1)求证:四边形BEDF是菱形.
(2)如图2,连接CO,若AE=2,AD=6,求cos∠BCO的值.
31.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=2,AD=4,求EC的长;
(3)若AE﹣DE=2EC,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A C B B A C D A
1.【解答】解:∵四边形ABCD是正方形,△ABP是等边三角形,
∴AB=BP=BC,∠ABC=90°,∠ABP=60°,
∴∠DAP=∠CBP=30°,
∴∠BCP=∠BPC=75°,故①正确;
∵AD=BC,AP=BP,∠DAP=∠CBP=30°,
∴△DAP≌△CBP(SAS),故②正确;
如图,∵△ABP是等边三角形,过点P作PG⊥AB于点G,PH⊥AD于点H,
∴AG=GB,
∵∠BAD=∠AGP=90°,
∴四边形AGPH是矩形,
∴PH=AG,
∵S△ABCBC×ABAD×AB,S△ADPAD×PHADABAD×AB,
∴△ADP和△ABC的面积比为1:2,故③正确;
∵∠PCD=∠BCD﹣∠BCP=15°,PC=PD,
∴∠PCD=∠PDC=15°,
∴∠CPN=30°,
∵CN⊥DP,
∴CNPC,
∴S△PDCDP×CNPC2,故④正确,
综上所述:①②③④.
故选:D.
2.【解答】解:由翻折变换可知,AD=AF,∠DAE=∠FAE,DE=FE,∠D=∠AFE,
∴∠AFG=180°﹣∠AFE=90°=∠B,
在Rt△ABG和Rt△AFG中,
,
∴Rt△ABG≌Rt△AFG(HL),因此①正确;
∴∠BAG=∠FAG,
又∵∠BAG+∠FAG+∠DAE+∠FAE=90°,
∴∠GAE=∠FAG+∠FAE90°=45°,因此②正确;
由翻折变换可知,DE=EF,
由全等三角形可知BG=GF,
设正方形的边长为a,BG=x,DE=EFa,则CG=a﹣x,GE=xa,EC=aaa,
在Rt△ECG中,由勾股定理得,
EC2+GC2=EG2,
即(a)2+(a﹣x)2=(xa)2,
解得xa,
即BGaBC,
∴BG=CG,因此③正确;
∴BG=CG=FG,
∴∠GCF=∠GFC,
由三角形全等可得,∠AGB=∠AGF,
又∵∠AGB+∠AGF+∠FGC=180°=∠FGC+∠GCF+∠GFC,
∴∠ABG=∠FCG,
∴AG∥FC,因此④正确,
∵BG=CG,
∴BGAB,
∴tan∠AGB=2,
∴∠AGB≠60°,
∵AG∥CF,
∴∠FCG=∠AGB≠60°,
∴△GCF不是等边三角形,因此⑤不正确;
故选:C.
3.【解答】解:∵正方形ABCD的边长为12,
∴AD=CD=12,∠ADF=∠CDF=45°.
∵DF=DF,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAE=∠FCD.
∵E为CD的中点,
∴.
∴.
故选:A.
4.【解答】解:∵点E在正方形ABCD内部,且△ABE是等边三角形,BD是正方形的对角线,
∴∠ADB=45°,∠DAE=90°﹣60°=30°,AD=AE,
∴∠BDE(180°﹣∠DAE)(180°﹣30°)=75°,
∴∠BDE=∠ADE﹣∠ADB=75°﹣45°=30°,
故选:C.
5.【解答】解:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠A=∠B=∠BCD=90°,
在△CBF和△DCE中,
,
∴△CBF≌△DCE(SAS),
∴∠BCF=∠CDE,
∵∠BCD=∠BCF+∠DCF=90°,
∴∠CDE+∠DCF=90°,
∴∠DMC=180°﹣(∠CDE+∠DCF)=90°,
∴△DMF为直角三角形,
∵点N为DF的中点,
∴MNDF,
∵AF=1,CE=BF=2,
∴AB=AF+BF=3,
在Rt△ADF中,AD=AB=3,AF=1,
由勾股定理得:DF,
∴MNDF.
故选:B.
6.【解答】解:连接CB,
根据三角形的外角等于和它不相邻的两个内角之和可得,∠M+∠N=∠3,∠H+∠G=∠4,∠3=∠1+∠KEF,∠4=∠2+∠KEF,
∴∠M+∠N+∠H+∠G=∠3+∠4=∠1+∠2+2∠KEF=180°+120°=300°,
∵∠KEF=120°,
∴∠FEC=∠5+∠6=180°﹣∠KEF=180°﹣120°=60°,
∵∠A+∠D+∠7+∠5+∠6+∠8=360°,
∴∠A+∠D+∠7+∠8=360°﹣60°=300°,
∴∠A+∠ABE+∠ECD+∠D+∠H+∠G+∠M+∠N=600°.
故选:B.
7.【解答】解:延长CE交AB于点H,过点E作EM⊥AB于点M,ME的延长线交CD于点N,过点F作FP⊥BC于点P,如图所示:
∵四边形ABCD是正方形,
∵AB=BC=CD=AD,AB∥CD,∠ABC=∠BCD=90°,
∴△BEH∽△DEC,
∴,
∵DE=2BE,
∴,
∴BHCDAB,HECE,
设BH=a,则AB=2a,
∴AB=BC=CD=AD=2a,
在Rt△BCH中,由勾股定理得:CH,
∵HECE,
∴HECH,CECH,
∵MN⊥AB,
∴∠BMN=∠MNC=∠ABC=90°,
∴四边形MNCB是矩形,
∴MN=BC=2a,EN⊥CD,
∵AB∥CD,
∴△BEM∽△DEN,
∴,
∴EMEN,
∴EMMN,ENMN,
∵DF⊥CE,
∴由三角形的面积公式得:S△BECCE DFCD EN,
∴CE DF=CD EN,
∴,
∴DF,
在Rt△DCF中,由勾股定理得:CF,
∵FP⊥CD,DF⊥CE,
∴∠CPF=∠DFC=90°,
∴∠PCF+∠CFP=90°,
∵∠PCF+∠DCF=∠BCD=90°,
∴∠CFP=∠DCF,
∴△CFP∽△DCF,
∴,
∴,
∴FP,PC,
∴BP=BC﹣PC,
在Rt△BFP中,由勾股定理得:BF,
∴ .
故选:A.
8.【解答】解:∵四边形DECF是正方形,
∴DE=DF,DE∥AC,∠DEB=∠AFD=90°,
∴∠BDE=∠A,
∴△BDE∽△DAF,
∴,设DE=3k,AF=5k,
在Rt△ADF中,则有25=9k2+25k2,
∴k2,
∴S△ADF 3k 5k,
∵,
∴S△BDE,
∴S△ADF+S△BDE7.5,
故选:C.
9.【解答】解:连接AG,
∵E、F分别为AH、GH的中点,
∴EFAG,
∴当AG最小时,EF最小,当AG⊥BC时,AG最小,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=120°,
∴∠B=60°,
∴当AG⊥BC时,∠AGB=90°,
∴sinB=sin60°,
∴AG=4,
∴EF的最小值42.
故选:D.
10.【解答】解:设③的边长为a,④的边长为b,②的宽为x,
∴⑤的边长为a+b,②的长为:a+a+b=2a+b,①的长为x+a,宽为b﹣a,
∴②的周长为:2(2a+b+x)=4a+2b+2x,
∵①的周长=2(x+a+b﹣a)=2x+2b,③的周长为4a,
∴①与③的周长和为:4a+2b+2x,
∴甲的说法正确;
∵①的周长=2(x+a+b﹣a)=2x+2b,⑤的周长为2(a+b)=2a+2b,
∴①与⑤的周长和为:2a+2b+2x+2b=2a+4b+2x,
∴乙的说法错误;
∵③的周长=4a,④的周长=4b,
∴③与④的周长和为:4a+4b,
∴丙的说法错误;
∵⑤的周长为2(a+b)=2a+2b,①的周长=2(x+a+b﹣a)=2x+2b,
∴⑤与①的周长差为:2a+2b﹣2x﹣2b=2a﹣2x,
∴丁的说法错误;
综上可知:说法正确的只有甲,
故选:A.
二、填空题
11.【解答】解:连接AP,如图1所示:
∵在Rt△ABC中,∠BAC=90°,PE⊥AB,PF⊥AC,
∴四边形AEPF是矩形,
∴EF=AP,
∵点P为斜边BC上的一个动点,
∴线段EF的最小值为线段AP的最小值,由点P到直线BC的距离中垂线段最短,过A作AP⊥BC,如图2所示:
在Rt△ABC中,∠BAC=90°,AB=3,AC=4,则由勾股定理可得,
∴由等面积法可得,即3×4=5AP,解得,
故答案为:.
12.【解答】解:如图,
∵四边形ABCD是正方形,
∴BC=CD,∠BCE=∠CDF=90°,
∵CE=DF,
∴△BCE≌△CDF(SAS),
∴∠EBC=∠FCD,
∵∠FCD+∠BCG=90°,
∴∠CBE+∠BCG=90°,
∴∠CGB=90°,
∴点G的运动轨迹是以BC为直径的⊙O,
当O,G,D共线时,DG的值最小,最小值,
故答案为.
13.【解答】解:连接AC,过A作AM⊥BC于M,在BC上截取BK=BE,连接GK,
∵四边形ABCD是菱形,
∴∠ABC=∠CBD,BC=BA,BC∥AD,
∵BG=BG,
∴△BGK≌△BGE(SAS),
∴GK=GE,∠BEG=∠BKG,
∵GF+GE=3,
∴GF+GK=3,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AMAB23,
∴GF+GK=AM,
∴F、G、K共线,且FK⊥BC,
∴∠BEG=∠BKG=90°,
∵AD∥BC,
∴FK⊥AD,
∴∠GFD=90°,
∵四边形ABCD是菱形,
∴∠GBE=∠GDF∠ABC=30°,AB=AD=2,
∴BEGE,DFGF,
∴BE+DF(GE+GF)=3,
∴AE+AF=BA+AD﹣(BE+DF)=223.
故答案为:.
14.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
15.【解答】解:因为点D(5,3)在边AB上,四边形OABC是正方形,
所以AB=BC=5,BD=5﹣3=2;
(1)若以C为中心,把△CDB顺时针旋转90°,
则点D′在x轴上,OD′=2,
所以D′(﹣2,0);
(2)若以C为中心,把△CDB逆时针旋转90°,
则点D′到x轴的距离为10,到y轴的距离为2,
所以D′(2,10),
综上,旋转后点D的对应点D′的坐标为(﹣2,0)或(2,10).
故答案为:(﹣2,0)或(2,10).
16.【解答】解:由题意可得:AB=CD=4,AD=BC=6,AD∥BC,
∴,
∴△EFG∽△DAG,
∴,
∴,
过点G作GH⊥BC于点H,
∴GH∥CD,EC=EF+FC=4,
∴△EHG∽△ECD,
∴,
∴,,
∴BH=BE+EH=2+1=3,且∠EHG=90°,
∴,
∴,
故答案为:.
17.【解答】解:①过点G作GP⊥AD于P,GQ⊥CD于Q,如图,
∵正方形ABCD,
∴∠ADC=90°,DB平分∠ADC,
∵GP⊥AD,GQ⊥CD,
∴GP=GQ,∠GPD=∠GQD=90°,
∴∠PGQ=90°,即∠FGQ+∠FGP=90°,
∵AG⊥GF,
∴∠FGP+∠PGA=∠FGA=90°,
∴∠FGP=∠PGA,
∴△FGQ≌△AGP(ASA),
∴AG=FG,故①正确;
②∵AG=FG,∠FGA=90°,
∴∠GAF=∠GFA=45°,
∵∠BAD=90°,
∴∠BAG+∠DAF=45°,
将△ABG绕点A逆时针旋转90度,得到△ADM,
则AM=AG,DM=BG,∠DAM=∠BAG,∠ADM=∠ABG=45°,
∴∠HDM=∠HDA+∠ADM=45°+45°=90°,
∴DM2+DH2=HM2,
∴∠HAM=∠HAD+∠DAM=∠HAD+∠BAG=45°=∠GAH,
∵AH=AH,
∴△AMH≌△AGH(SAS),
∴GH=HM,
∴BG2+DH2=GH2,故②正确;
③∵,
∴,
∴,
∴,
∴∠DHM=30°,
∴∠GHM=180°﹣∠DHM=150°;
∵△AMH≌△AGH,
∴,
∴∠BGE=∠AGH=180°﹣∠GAH﹣∠GHA=180°﹣45°﹣75°=60°,故③正确;
④将△ABE绕点A逆时针旋转90度,得到△ADN,连接EF,
则DN=BE,AN=AE,
同理可得△AEF≌△ANF,
∴EF=FN=FD+DN=FD+BE,∠AFE=∠AFN,
由∠AHG=75°,
∴∠FHD=75°,
∵∠FDH=45°,
∴∠AFD=180°﹣∠FHD﹣∠FDH=60°,
∴∠AFE=∠AFN=60°,
∴∠EFC=180°﹣∠AFD﹣∠AFE=60°,
∴∠CEF=30°,
∴,
由勾股定理,得EF2=CE2+CF2,
即,
∴,
∴,故④错误;
∴正确有①②③.
故答案为:①②③.
18.【解答】解:连接AG并延长AG交CD于点P,连接PF,如图所示,
∵四边形ABCD是正方形,
∴CD=BC=AB=4,∠C=90°,AB∥CD,
∴∠AEG=∠GDP,
∵E、F分别为边AB、BC的中点,
∴AEAB=2,CFBC=2.
∵G为DE的中点,
∴EG=DG,
在△EAG和△DPG中,
,
∴△EAG≌△DPG(ASA).
∴AG=PG,DP=AE=2.
∴G为AP的中点,
∵H为AF的中点,
∴GH是△APF的中位线.
∴GHPF.
在Rt△FCP中,
CP=DC﹣DP=4﹣2=2,
∴PF2.
∴GHPF.
故答案为:.
19.【解答】解:如图,在AD,BC上截取线段AM,BN,使得AM=BN,连接MN交EF于点K.连接CK,CK的中点为O.
∵四边形ABCD是矩形,
∴AD=BC=4,AD∥BC,∠A=90°,
∵AM=BN,
∴四边形ABNM是平行四边形,
∵∠A=90°,
∴四边形ABNM是矩形,
∴∠AMN=∠MNB=90°,AB=MN=3,
∵FM∥EN,
∴△MKF∽△NKE,
∴,
∴KNMN3,
∵∠CNK=90°,CN=4,
∴CK,
∵CG⊥EF,
∴∠CGK=90°,
∵OK=OC,
∴OG=OK=OC=ON,
∴点G在⊙O上运动,
∴CG的最大值=CK.
故答案为:.
20.【解答】解:∵正方形ABCD,
∴,
作∠CDN=30°,
∵以GE为边作等边△EFG,点F落在CD上,M 为GF中点,
∴EM⊥GF,
∴∠EMF=90°,,
∵四边形ABCD是正方形,
∴∠EDF=90°,
∴点E、D、F、M四点共圆,所以∠MDF=∠MEF=30°,
∴当点E在AD上运动时,点M在DN上运动,当CM⊥DN时,CM最小,
∵∠CDN=30°,
∴CM最小值,
故答案为:.
三、解答题
21.【解答】(1)①证明:过G作GM⊥BC于M,
∵正方形ABCD,
∴AB=BC=CD=DA,∠D=∠C=∠GMC=90°,
∴四边形MGDC是矩形,
∴AD=DC=GM,∠ADE=∠GMF=∠AGM=90°,
∵GH⊥AE,
∴∠MGF=90°﹣∠AGF=∠DAE,
∵
∴△ADE≌△GMF(ASA),
∴AE=GF.
②过点H作HM⊥DC于点M,
∵E为CD的中点,不妨设DE=EC=x
∵正方形ABCD,
∴AD=DC=2x,∠ADC=90°,
∴,
∵DF⊥AE于点H,
∴,
∴,,
∴,
∴,
∴,
∴,
∴.
(2)如图,以点D为原点,以DC所在直线为x轴建立平面直角坐标系,
∵AB=6,AG=CF=1.5,且CE=2DE,
∴CE=4,DE=2,
∴A(0,6),E(2,0),,
设直线AE的解析式为y=kx+b,
根据题意,得,
解得,
∴直线AE的解析式为y=﹣3x+6;
设直线GF的解析式为y=px+q,
根据题意,得,
解得,
∴直线GF的解析式为;
由此得,
解得,
故点,
∴,
设直线GF与x轴的交点为P,
∴点P(9,0),
∴PE=9﹣2=7,,
∴,
过点E作EQ⊥GF于点Q,
∴,
∴,
∴HQ=EQ,
∴∠EHQ=45°,
∴∠AHG=45°.
22.【解答】解:(1)①∵菱形的对角线互相垂直,
∴菱形是“理正四边形”,
∵平行四边形、矩形的对角线不一定垂直,
∴不一定是“理正四边形”,
故答案为:菱形;
②若四边形ABCD是“理正四边形”,则AC⊥BD,
∵AB=AD,
∴OB=OD,
∴AC是BD的垂直平分线,
∴CB=CD,
又∵CB≠CD,
∴四边形ABCD不是“理正四边形”.
故答案为:不是;
(2)∵四边形ABCD是面积为1的“理正四边形”,
∴,
∴BD AC=2,
∵AC﹣BD=3,
∴(AC+BD)2=(AC﹣BD)2+4AC BD=32+4×2=17,
∴,
联立,
解得,
∴;
(3)如图,过E作EM⊥BD于M,EN⊥AC于N,
∵EM⊥BD,EN⊥AC,
∴∠MON=∠OME=∠ONE=90°,
∴四边形OMEN是矩形,
∴OM=NE,ME=ON,
设ME=ON=m,OM=NE=n,
∵EA=EB=EC=ED=3,
在Rt△DME中,ME2+MD2=DE2,
∴,
在Rt△NEC中,NE2+NC2=CE2,
∴,
∴,
整理得,
解得:,
∴,
在Rt△MEO中,ME2+MO2=OE2,
∴m2+n2=OE2,
∵1≤OE≤2,
∴1≤OE2≤4,
∴1≤m2+n2≤4,
∵E是第一象限内的动点,
∴m>0,n>0,
∴0<m2<4,
∴9﹣m2>0,
∵1≤m2+n2≤4,
1﹣m2≤n2≤4﹣m2,
∴m2﹣4≤﹣n2≤m2﹣1,
∴m2+5≤9﹣n2≤m2+8,
∴,
∴,
∴,
∴,
∵0<m2<4,
∴当m2=4时,,
当m2=0时,,
∴,
∴.
23.【解答】解:(1)如图1,作EG⊥AB于点G,则EG∥x轴,
∵四边形ABCO为矩形,A点在x轴上,C点在y轴上,O(0,0),E(0,2),B(8,12),
∴G(8,2),C(0,12),
由折叠得EF=CE=12﹣2=10,
∵∠EGF=90°,EG=8,
∴FG6,
∴AF=AG+FG=2+6=8,
∴F(8,8).
(2)如图2,作PH⊥y轴于点H,
∵△PDE≌△CED,
∴DP=EC,∠PDE=∠CED,
∵EC=EF,∠CED=∠FED,
∴DP=EF,∠PDE=∠FED,
∴DP∥EF,
∴四边形PDFE是平行四边形,
∵∠DPE=∠ECD=90°,
∴四边形PDFE是矩形,
∴∠PEF=∠EFD=90°,
∴∠HEP+∠CEF=90°,∠BFD+∠AFE=90°,
∵AB∥OC,
∴∠CEF=∠AFE,
∴∠HEP=∠BFD,
∵∠PHE=∠DBF=90°,PE=DF,
∴△PHE≌△DBF(AAS),
∵AB=12,AF=8,BC=8,
∴BF=AB﹣AF=12﹣8=4,DF=DC=8﹣BD,
∵∠B=90°,
∴BF2+BD2=DF2,
∴42+BD2=(8﹣BD)2,
∴BD=3,
∴HP=BD=3,HE=BF=4,DF=DC=8﹣3=5,
∴OH=2+4=6,
∴P(﹣3,6).
(3)存在,设直线DE交x轴于点L,
如图3,四边形FDMN是平行四边形,且点M在线段DE上,
作MQ⊥x轴于点Q,则∠MQN=∠FBD=90°,
∵FN∥DM,BC∥OA,
∴∠ANF=∠ALD=∠CDE,
∴∠FNM=∠MDF,
∴180°﹣∠ANF﹣∠FNM=180°﹣∠CDE﹣∠MDF,
∴∠MNQ=∠FDB,
∵MN=FD,
∴△MNQ≌△FDB(AAS),
∴QM=BF=4,
设M(x,4),设直线DE的解析式为y=kx+2,
∵D(5,12),
∴5k+2=12,
解得k=2,
∴直线DE的解析式为y=2x+2,
把M(x,4)代入y=2x+2得2x+2=4,
解得x=1,
∴M(1,4);
如图4,四边形FDMN是平行四边形,且点M在DE的延长线上,
作MR⊥x轴于点R,则∠MRN=∠FBD=90°,作CW∥DF交x轴于点W,
∵MN∥DF,
∴CW∥DF,
∴∠MNR=∠OWC=∠WCB=∠FDB,
∵MN=FD,
∴△MNR≌△FDB(AAS),
∴RM=BF=4,
设M(x,﹣4),
把M(x,﹣4)代入y=2x+2得2x+2=﹣4,
解得x=﹣3,
∴M(﹣3,﹣4);
如图5,四边形FDMN是平行四边形,且点M在ED的延长线上,
作MT⊥CD交CB的延长线于点T,则∠T=∠FAN=90°,
∵FN∥DM,
∴∠MDT=∠MLA=∠FNA,
∵MD=FN,
∴△MDT≌△FNA(AAS),
∴TM=AF=8,
∴yM=12+8=20,
设M(x,20),
把M(x,20)代入y=2x+2得2x+2=20,
解得x=9,
∴M(9,20),
综上所述,点M的坐标为(1,4)或(﹣3,﹣4)或(9,20).
24.【解答】解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠BAD=∠EAF+∠DAF=90°,
∵AF⊥DE,
∴∠AFD=∠AFE=90°,
∴∠ADF+∠DAF=90°
∴∠EAF=∠ADE,
∵E是AB的中点,
∴,
∴,
在Rt△AEF中,,
∴,
在Rt△ADE中,;
(2)∵BD是正方形ABCD的对角线,
∴
由(1)得∠AFE=90°,
∴,
同理,得,
∴,
又∵AE=BE,
∴,
又∵∠BEF=∠DEB,
∴△BEF∽△DEB,
∴∠BFE=∠DBE=45°.
∴∠AFB=90°+45°=135°;
(3)OF⊥FB且 FB=2OF,
理由如下:
由(2)得△BEF∽△DEB,
∴,
∵O是BD的中点,
∴,
∵,∠AFE=90°,
∴,
∴,
即,
在△ABF中,∠BAF=180°﹣∠AFB﹣∠ABF=45°﹣∠ABF,
而∠DBF=45°﹣∠ABF,
∴∠EAF=∠OBF,
∴△BFO~△AFE,
∴,∠BFO=∠AFE=90°,
∴BF=2OF,BF⊥OF.
25.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=∠C=90°,
∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
∴BC=BF,∠FBE=∠EBC,∠C=∠BFE=90°,
∵BC=2BA,
∴BF=2BA,
∴∠AFB=30°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFB=∠CBF=30°,
∴∠CBE∠CBF=15°;
(2)∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
∴∠BFE=∠C=90°,CE=EF,
在矩形ABCD中,∠A=∠D=90°,AB=CD,
∴∠AFB+∠DFE=90°,∠DEF+∠DFE=90°,
∴∠AFB=∠DEF,
∴△FAB∽△EDF,
∴,
∴AF DF=AB DE,
∵DE=4,AF FD=40,
∴AB=10=CD,
∴CE=CD﹣DE=10﹣4=6,
∴EF=6,
∴DF2,
∴AF4,
∴BC=AD=AF+DF=6;
(3)如图3,过点N作NG⊥BF于点G,
∵∠NFG=∠AFB,∠NGF=∠BAF=90°,
∴△NFG∽△BFA,
∴,
∵BC=BF=5,NF,
∴,
∴NGAB,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG,
又∵BN=BN,
∴Rt△ABN≌Rt△GBN(HL),
∴AB=BG,
∴FG=BF﹣BG=5﹣AB,
在Rt△NGF中,NG2+FG2=NF2,
∴(AB)2+(5﹣AB)2=()2,
∴AB=4或AB=5(舍去),
∴AB的值为4.
26.【解答】(1)证明:∵EF垂直平分AC,
∴EF⊥AC,AO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OCF=∠OAE,
在△AOE 与△COF中,
,
∴△AOE≌△COF(AAS),
∴FO=EO,
又∵CO=AO,
∴四边形AFCE是平行四边形,
又∵EF⊥AC,
∴平行四边形AFCE为菱形;
(2)解:∵OC=CG,
∴∠COG=∠G=15°,
∴∠ACB=∠COG+∠G=30°,
∵四边形AFCE为菱形,
∴O为AC的中点,
∵F为线段BC的中点,
∴OF是三角形ABC的中位线,
∴,
∵EF⊥AC,
∴,,
∴,,
如图,作 OH⊥BC,垂足为H,则∠OHG=90°,
∴,
则.
27.【解答】(1)证明:∵四边形形OABC是矩形,
∴OC∥AB,
∴∠COB=∠OBA,∠OPE=∠PEB,
∵D为OB中点,
∴OD=BD,
∴△OPD≌△BED(AAS),
∴OP=BE,
又∵OC∥AB,即OP∥BE,
∴四边形OPBE为平行四边形;
(2)解:∵O(0,0),B(6,8),
∴OB中点D坐标为(3,4),
设P(0,t),则OP=t,
∴S△OPDt 3,
设PD的直线表达式为y=kx+t,
∵D在PD上,
∴4=3k+t,
∴k,
∴PD:y.
令x=6,则y=﹣t+8,
∴E(6,8﹣t).
∴S四边形OAED=S△AED+S△ODA(8﹣t)+1224.
∵S△OPD:S四边形OAED=1:3,
∴24=3,
解得:t=4,
∴P(0,4).
(3)解:Q的坐标为(3,9)或(﹣3,4)或(3,).
如图,以OD为边,四边形ODQP为菱形,
∵D(3,4),
∴OD5,
∴Q(3,9);
如图,以OD为边,四边形ODPQ为菱形,
∴点D与点Q关于y轴对称,
∴Q(﹣3,4);
如图,以OD为对角线,四边形OQDP为菱形,延长DQ交x轴于点H,则QH⊥x轴,
设OQ=DQ=m,则QH=4﹣m,
∴32+(4﹣m)2=m2,
∴m,
∴DQ,
∴QH=4,
∴Q(3,).
综上所述,Q的坐标为(3,9)或(﹣3,4)或(3,).
28.【解答】(1)证明:在正方形ABCD中 CB=CD,∠B=∠CDA=90°,
∴∠CDF=∠B=90°.
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS).
∴CE=CF;
(2)证明:GE=BE+GD成立.理由如下:
∵∠BCD=90°,∠GCE=45°,
∴∠BCE+∠GCD=45°.
∵△BCE≌△DCF(已证),
∴∠BCE=∠DCF.
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=45°.
∴∠ECG=∠FCG=45°.
在△ECG和△FCG中,
,
∴△ECG≌△FCG(SAS).
∴GE=FG.
∵FG=GD+DF,
∴GE=BE+GD;
(3)①如图2,过点C作CG⊥AD,交AD的延长线于点G,
由(2)和题设知:DE=DG+BE,
设DG=x,则AD=6﹣x,DE=x+3,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(6﹣x)2+32=(x+3)2,
解得x=2.
∴DE=2+3=5;
②把△ABE旋转120°得到△ADE′,则DE′=BE=2,DF=4,EF=E′F,∠ADE′=∠B=60°,
∴∠E′DF=120°,
过E′作E′H⊥FD于H,∠E′DH=60°,
∴DHDE′=1,HE′DE′,
∴EF2.
故答案为:2.
29.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠ADB=∠DBC,
∵∠EPD=∠ABC,∠EBP+∠BEP=∠EPD,∠EBP+∠DBC=∠ABC,
∴∠BEP=∠DBC,
∴∠BEP=∠ADB,
在△PBE和△ABD中,
∴△PBE≌△ABD(AAS);
(2)解:过点D作DF⊥BC,交BC的延长线于点F,如图,
∵AB∥CD,
∴∠DCF=∠ABC,,
∴DF=CD sin∠DCF=12,
∴,
∴BF=BC+CF=16,
∴,
由(1)得∠BEP=∠ADB,∠PBE=∠ABD,
∴△PBE△ABD,
∴,
∵AB=BE,
∴;
(3)解:△APE是以AP为底的等腰三角形,即AE=PE,
①当点E在线段AB上时,如图,
∵△PBE∽△ABD,
∴,
∵BE=AB﹣AE=AB﹣PE,
∴,
解得,
∴;
②当点E在BA延长线上时,如图,
∵△PBE∽△ABD,
∴,
∵BE=AB+AE=AB+PE,
∴,
解得,
∴.
综上所述,x的值为或;
(4)解:∠ADE的正切值为.
过E作EF⊥AD于点F,
由(2)知△PBE△ABD,
∴,
∴,
∴BE,
∴AE=BE﹣AB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ABC=∠DAE,
∴sin∠ABC=sin∠DAE,
∴EF=AE sin∠DAE=(),
∴AF,
∴DF=7﹣()=16,
∴tan∠ADE.
30.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,
∴∠EDO=∠FBO,DE∥BF,
∵EF是BD的垂直平分线,
∴OB=OD,BE=DE,
∴∠BDF=∠DBF,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA),
∴DE=BF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∵EF是BD的垂直平分线,
∴BE=DE=AD﹣AE=6﹣2=4,
∴AB2,
∴BD4
∵OB=OD,∠BCD=90°,
∴OB=OC,
∴∠BCO=∠CBD=∠ADB,
∴cos∠BCO=cos∠ADB.
31.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由翻折可知,∠D=∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠CEF=90°,
∴∠AFB=∠FEC,
∴△ABF∽△FCE.
(2)设EC=x,
由翻折可知,AD=AF=4,
∴BF2,
∴CF=BC﹣BF=2,
∵△ABF∽△FCE,
∴,
∴,
∴x,
∴EC.
(3)∵△ABF∽△FCE,
∴,
∴tanα+tanβ,
设AB=CD=a,BC=AD=b,DE=x,
∴AE=DE+2CE=x+2(a﹣x)=2a﹣x,
∵AD=AF=b,DE=EF=x,∠B=∠C=∠D=90°,
∴BF,CF,
∵AD2+DE2=AE2,
∴b2+x2=(2a﹣x)2,
∴a2﹣axb2,
∵△ABF∽△FCE,
∴,
∴,
∴a2﹣ax ,
∴b2 ,
整理得,16a4﹣24a2b2+9b4=0,
∴(4a2﹣3b2)2=0,
∴,
∴tanα+tanβ.
21世纪教育网(www.21cnjy.com)
同课章节目录
