26. 3. 2 实践与探索(2) 同步练习 (无答案)2024-2025学年九年级下册数学华师版
文档属性
| 名称 | 26. 3. 2 实践与探索(2) 同步练习 (无答案)2024-2025学年九年级下册数学华师版 | 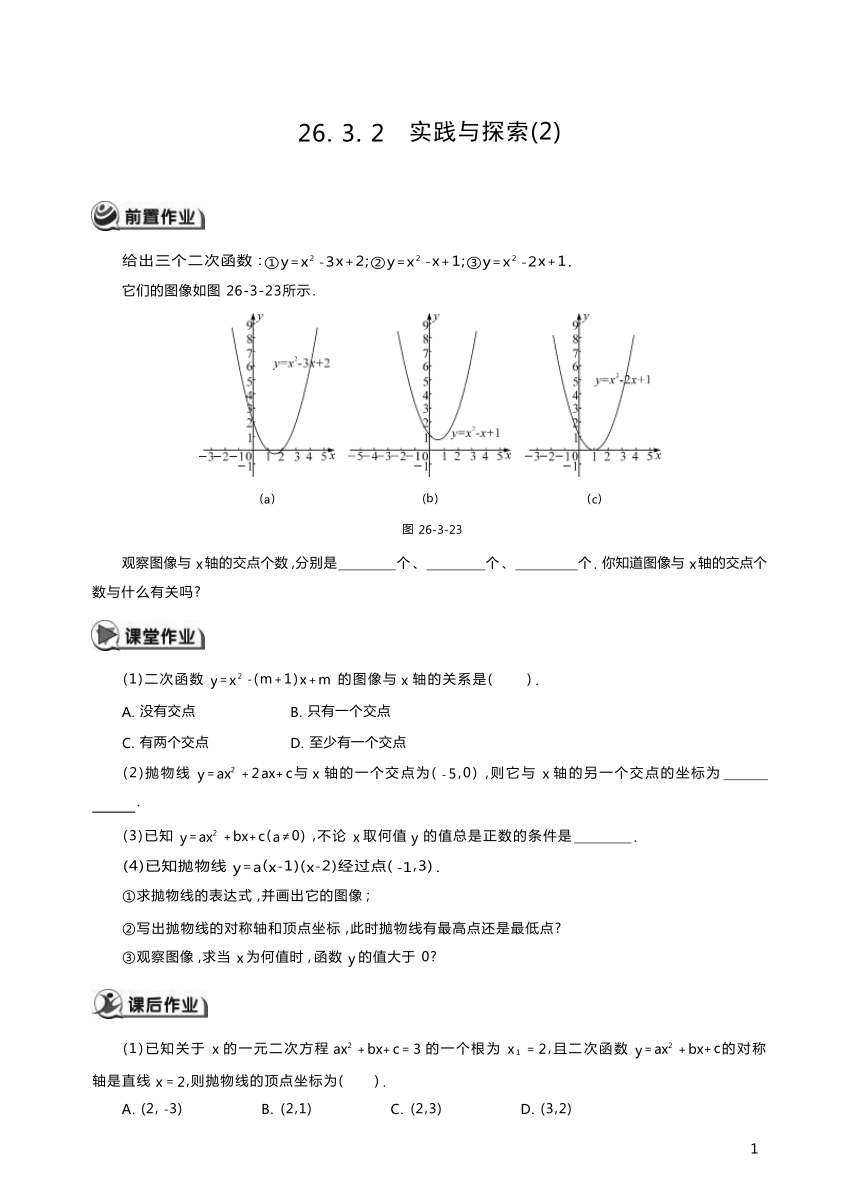 | |
| 格式 | docx | ||
| 文件大小 | 52.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 11:08:10 | ||
图片预览

文档简介
26. 3. 2 实践与探索(2)
给出三个二次函数 : ①y=x2 -3x+2;②y=x2 -x+1;③y=x2 -2x+1.
它们的图像如图 26-3-23所示 .
(a) (b) (c)
图 26-3-23
观察图像与 x 轴的交点个数 ,分别是 个 、 个 、 个 . 你知道图像与 x 轴的交点个 数与什么有关吗
(1)二次函数 y=x2 -(m+1)x+m 的图像与 x 轴的关系是( ) .
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 至少有一个交点
(2)抛物线 y=ax2 +2ax+c与 x 轴的一个交点为( -5,0) ,则它与 x 轴的另一个交点的坐标为
.
(3)已知 y=ax2 +bx+c(a≠0) ,不论 x 取何值 y 的值总是正数的条件是 .
(4)已知抛物线 y=a(x-1)(x-2)经过点( -1,3) .
①求抛物线的表达式 ,并画出它的图像 ;
②写出抛物线的对称轴和顶点坐标 ,此时抛物线有最高点还是最低点
③观察图像 ,求当 x 为何值时 , 函数 y 的值大于 0
(1)已知关于 x 的一元二次方程 ax2 +bx+c= 3 的一个根为 x1 = 2,且二次函数 y=ax2 +bx+c的对称 轴是直线 x = 2,则抛物线的顶点坐标为( ) .
A. (2, -3) B. (2,1) C. (2,3) D. (3,2)
1
(2)若抛物线 y=ax2 +bx+c的所有点都在 x 轴下方 ,则必有 ( ) .
A. a<0. b2 -4ac>0 B. a>0,b2 -4ac>0
C. a<0,b2 -4ac<0 D. a>0,b2 -4ac<0
(3)二次函数 y= x2 - 4x + 3 与 x 轴 有 两 个 交 点 , 即 方 程 x2 - 4x + 3 = 0 有 的 实 数 根 ,x1 = ,x2 = .
(4)已知抛物线 y=ax2 +bx+c的图像与 x 轴有两个交点,那么一元二次方程 ax2 +bx+c= 0 的根的情 况是 .
(5)二次函数 y=ax2 +bx+c(a≠0,a,b,c是常数)中 , 自变量 x 与函数 y 的对应值如下表所示 .
x … -1 (
1
2
) 0 1 2 1 2 3 …
y … -2 1 - 4 1 7 4 2 1 1 - 4 -2 …
①判断二次函数图像的开口方向 ,并写出它的顶点坐标 ;
②一元二次方程 ax2 +bx+c= 0(a≠0,a,b,c是常数)的两个根 x1 ,x2 的取值范围是( ) .
C. -2
给出三个二次函数 : ①y=x2 -3x+2;②y=x2 -x+1;③y=x2 -2x+1.
它们的图像如图 26-3-23所示 .
(a) (b) (c)
图 26-3-23
观察图像与 x 轴的交点个数 ,分别是 个 、 个 、 个 . 你知道图像与 x 轴的交点个 数与什么有关吗
(1)二次函数 y=x2 -(m+1)x+m 的图像与 x 轴的关系是( ) .
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 至少有一个交点
(2)抛物线 y=ax2 +2ax+c与 x 轴的一个交点为( -5,0) ,则它与 x 轴的另一个交点的坐标为
.
(3)已知 y=ax2 +bx+c(a≠0) ,不论 x 取何值 y 的值总是正数的条件是 .
(4)已知抛物线 y=a(x-1)(x-2)经过点( -1,3) .
①求抛物线的表达式 ,并画出它的图像 ;
②写出抛物线的对称轴和顶点坐标 ,此时抛物线有最高点还是最低点
③观察图像 ,求当 x 为何值时 , 函数 y 的值大于 0
(1)已知关于 x 的一元二次方程 ax2 +bx+c= 3 的一个根为 x1 = 2,且二次函数 y=ax2 +bx+c的对称 轴是直线 x = 2,则抛物线的顶点坐标为( ) .
A. (2, -3) B. (2,1) C. (2,3) D. (3,2)
1
(2)若抛物线 y=ax2 +bx+c的所有点都在 x 轴下方 ,则必有 ( ) .
A. a<0. b2 -4ac>0 B. a>0,b2 -4ac>0
C. a<0,b2 -4ac<0 D. a>0,b2 -4ac<0
(3)二次函数 y= x2 - 4x + 3 与 x 轴 有 两 个 交 点 , 即 方 程 x2 - 4x + 3 = 0 有 的 实 数 根 ,x1 = ,x2 = .
(4)已知抛物线 y=ax2 +bx+c的图像与 x 轴有两个交点,那么一元二次方程 ax2 +bx+c= 0 的根的情 况是 .
(5)二次函数 y=ax2 +bx+c(a≠0,a,b,c是常数)中 , 自变量 x 与函数 y 的对应值如下表所示 .
x … -1 (
1
2
) 0 1 2 1 2 3 …
y … -2 1 - 4 1 7 4 2 1 1 - 4 -2 …
①判断二次函数图像的开口方向 ,并写出它的顶点坐标 ;
②一元二次方程 ax2 +bx+c= 0(a≠0,a,b,c是常数)的两个根 x1 ,x2 的取值范围是( ) .
C. -
