第27章 圆 评估检测题(A卷)(无答案)2024-2025学年九年级下册数学华师版
文档属性
| 名称 | 第27章 圆 评估检测题(A卷)(无答案)2024-2025学年九年级下册数学华师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 100.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览

文档简介
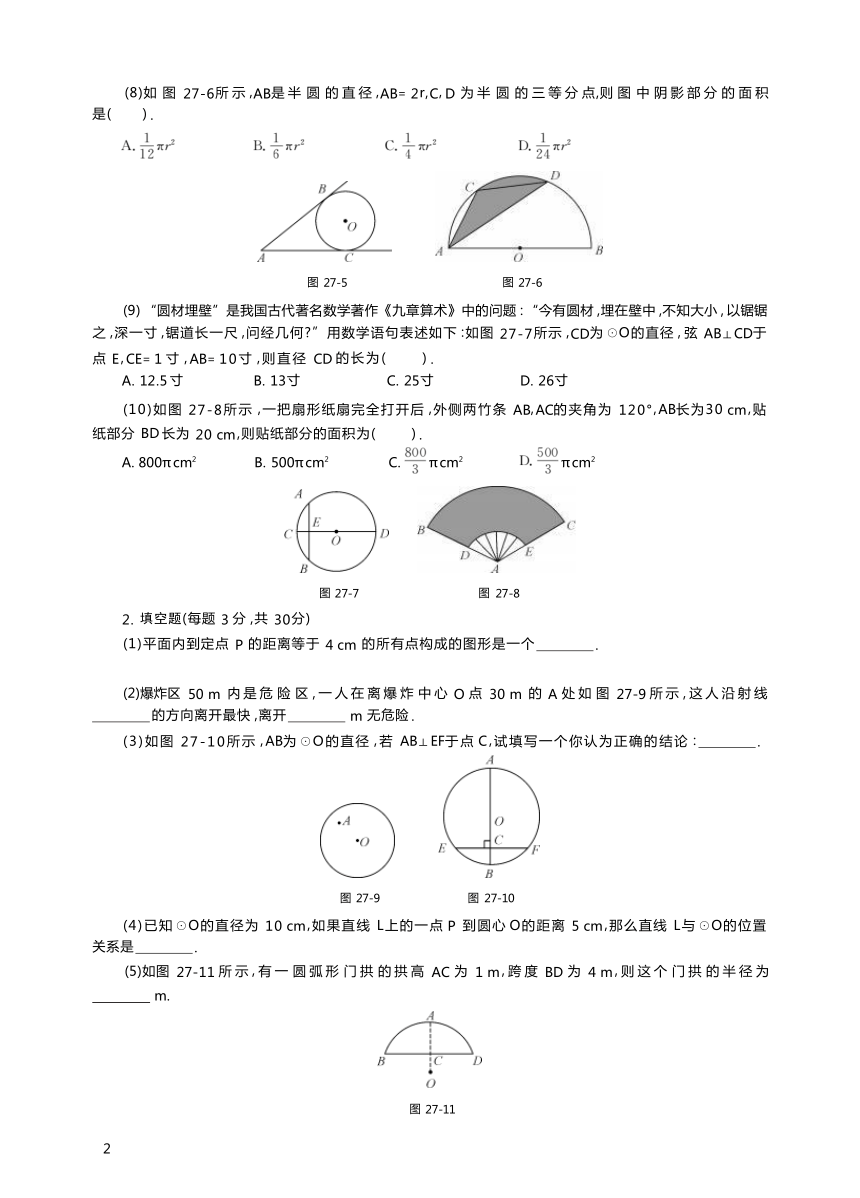
第 27章评估检测题(A卷)
(时间 :120分钟 总分 :100分)
1. 选择题(每题 3 分 ,共 30分)
(1)如图 27-1所示 ,A,B,C,是 ☉O上的三点,∠BAC= 45°,则 ∠BOC的大小是( ) .
A. 90° B. 60° C. 45° D. 22.5°
(
︵
︵
)(2)如图 27-2所示 , 已知 ☉O中 ,AB= 2CD,则 AB与 CD 的关系是( ) .
A. AB= 2CD B. AB>2CD
C. AB<2CD D. 无法确定
图 27-1 图 27-2
(3)已知半径为 5 的圆中 , 圆心到弦 EF的距离为 4,则弦 EF的长为( ) .
A. 3 B. 4 C. 5 D. 6
—一
(4)如图 27-3所示 ,在 ☉O中 ,弦 AB的长等于 ☉O的半径 ,ACB为优弧 ,则 ∠ACB为( ) .
A. 30° B. 45° C. 60° D. 150°
图 27-3
(5)下列关于三角形的外心的说法中 ,正确的是( ) .
A. 三角形的外心在三角形外
B. 三角形的外心到三边的距离相等
C. 三角形的外心到三个顶点的距离相等
D. 等腰三角形的外心在三角形内
(6)如图 27-4所示 ,一块边长为 8 cm 的正方形木板 ABCD,在水平桌面上绕点 A按逆时针方向旋转至 A'B'C'D'的位置 ,则顶点 C从开始到结束所经过的路径长为( ) .
图 27-4
A. 8π cm B. 4 2 cm C. 16 cm D. 16 2 cm
(7)如图 27-5所示 ,AB,AC与 ☉O 相 切 于 B,C 两 点 , ∠A= 50°,点 P 是 圆 上 异 于 B,C 的 一 动 点,则
∠BPC的度数为( ) .
A. 65° B. 115° C. 65°或 115° D. 130°或 50°
1
(8)如 图 27-6所 示 ,AB是 半 圆 的 直 径 ,AB= 2r,C, D 为 半 圆 的 三 等 分 点,则 图 中 阴 影 部 分 的 面 积
是( ) .
图 27-5 图 27-6
(9) “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题 : “今有圆材 ,埋在壁中 ,不知大小 , 以锯锯 之 ,深一寸 ,锯道长一尺 ,问经几何 ”用数学语句表述如下 :如图 27-7所示 ,CD为 ☉O的直径 , 弦 AB⊥CD于
点 E,CE= 1 寸 ,AB= 10寸 ,则直径 CD 的长为( ) .
A. 12.5 寸 B. 13寸 C. 25寸 D. 26寸
(10)如图 27-8所示 ,一把扇形纸扇完全打开后 ,外侧两竹条 AB,AC的夹角为 120°,AB长为30 cm ,贴 纸部分 BD 长为 20 cm ,则贴纸部分的面积为( ) .
A. 800π cm2 B. 500π cm2 C. π cm2 π cm2
图 27-7 图 27-8
2. 填空题(每题 3 分 ,共 30分)
(1)平面内到定点 P 的距离等于 4 cm 的所有点构成的图形是一个 .
(2)爆炸区 50 m 内 是 危 险 区 , 一 人 在 离 爆 炸 中 心 O 点 30 m 的 A 处 如 图 27-9 所 示 , 这 人 沿 射 线 的方向离开最快 ,离开 m 无危险 .
(3)如图 27-10所示 ,AB为 ☉O的直径 ,若 AB⊥EF于点 C,试填写一个你认为正确的结论 : .
图 27-9 图 27-10
(4)已知 ☉O的直径为 10 cm ,如果直线 L上的一点 P 到圆心 O的距离 5 cm ,那么直线 L与 ☉O的位置 关系是 .
(5)如图 27-11 所 示 , 有 一 圆 弧 形 门 拱 的 拱 高 AC 为 1 m , 跨 度 BD 为 4 m , 则 这 个 门 拱 的 半 径 为
m.
图 27-11
2
(6)如图 27-12所示 ,有一个圆锥形粮堆 ,其主视图是边长为 6 m 的等边三角形 ,母线的中点 P 有一只 老鼠正在偷吃粮食 ,小猫从 B处沿圆锥表面去偷袭老鼠 ,则小猫所经过的最短路径是 m. (结果不 取近似数)
(7)要用圆形铁片截出边长为 4 cm 的正方形铁片 ,则选用的圆形铁片的直径最小要 cm.
(8)如图 27-13所示 , ☉O的半径为 1, 圆周角 ∠ABC= 30°,则图中阴影部分的面积是 . (结果用 π表示)
(9)若过 ☉O内一点 P 的最长的弦长为 10 cm ,最短弦长为 8 cm ,则 OP 的长为 cm.
图 27-12 图 27-13
(10)如图 27-14所示 ,一段铁路弯道成圆弧形 , 圆弧的半径是 0. 3 km,一列火车以36km/h的速度用了 10 s通过弯道 ,那么弯道所对的圆心角的度数为 . ( π取 3.14,结果精确到 0.1°)
图 27-14
3. 解答题(共 40分)
(1)海中有一小岛 ,它周围 20 n mile有暗礁 ,一船跟踪鱼群由西向东航行 ,在点 B测得小岛 A 在北偏东 60°方向上 ,航行 30 n mile到达点 C,这时小岛A在北偏东 30°处 ,如果渔船不改变航向 ,继续向东追踪捕捞 , 有没有触礁的危险 (5分)
(2)如图 27-15所示 , ☉C经过原点且与两坐标轴分别交于 A,B 两点,点 A 的坐标为(0,4) ,M 是圆上
一点,∠BMO= 120°,求 ☉C的半径和圆心 C的坐标 . (5分)
图 27-15
3
(3)如图 27-16所示 ,有一块直径是 1 m 的圆形铁皮 ,要从中剪出一个最大的圆心角是 90°的扇形 ABC. (5分)
①求被剪掉的阴影部分的面积 ;
②用剪下的扇形铁皮围成一个圆锥 ,该圆锥的底面圆的半径是多少 (结果可用根号表示)
图 27-16
(4)如图 27-17所示 ,AB是 ☉O的直径 ,BD 是 ☉O的弦 ,延长 BD 到点 C,使 DC= BD,连接 AC交 ☉O 于点 E. (5分)
①AB与 AC的大小有什么关系
②按角的大小分类 ,请你判断 △ABC是属于哪一类三角形 ,并说明理由 .
图 27-17
(5)已知 △ABC内接于 ☉O,过点 A作直线 EF. (5分)
①如图 27-18(a)所示 ,AB为 ☉O的直径 ,要使得 EF是 ☉O的切线 ,还需添加的条件是(只需写 出 两种
即可) :A. ;B. .
②如图 27-18(b)所示 ,AB为非直径的弦 ,且 ∠CAE= ∠B. 求证 :EF是 ☉O的切线 .
(a) (b)
图 27-18
4
(6)如图 27-19所示 ,BE是 ☉O的直径 ,BC切 ☉O 于点 B, 弦 ED∥OC, 连接 CD 并延长交 BE 的延长 线于点 A. (5分)
①证明 :CD 是 ☉O的切线 ;
②若 AD= 2,AE= 1,求 CD 的长 .
图 27-19
(7)如图 27-20所示 ,在直角梯形 ABCD 中 ,AB∥CD, 以 AD为直径的圆切 BC 于点 E,连接 OB,OC, 试探究 OB与 OC 有何位置关系 (5分)
图 27-20
(8)如图 27-21所示,点 P 在 ☉O 外 ,PC是 ☉O的切线 ,C为切点,直线 PO 与 ☉O 相交于点 A,B. (5 分)
①试探求 ∠BCP与 ∠P 的数量关系 ;
②若 ∠A= 30°,则 PB与 PA 有什么数量关系
③∠A可能等于 45°吗 若 ∠A= 45°,则过点 C的切线与 AB有怎样的位置关系
④若 ∠A>45°,则过点 C的切线与直线 AB 的交点 P 的位置将在哪里
图 27-21
5
(时间 :120分钟 总分 :100分)
1. 选择题(每题 3 分 ,共 30分)
(1)如图 27-1所示 ,A,B,C,是 ☉O上的三点,∠BAC= 45°,则 ∠BOC的大小是( ) .
A. 90° B. 60° C. 45° D. 22.5°
(
︵
︵
)(2)如图 27-2所示 , 已知 ☉O中 ,AB= 2CD,则 AB与 CD 的关系是( ) .
A. AB= 2CD B. AB>2CD
C. AB<2CD D. 无法确定
图 27-1 图 27-2
(3)已知半径为 5 的圆中 , 圆心到弦 EF的距离为 4,则弦 EF的长为( ) .
A. 3 B. 4 C. 5 D. 6
—一
(4)如图 27-3所示 ,在 ☉O中 ,弦 AB的长等于 ☉O的半径 ,ACB为优弧 ,则 ∠ACB为( ) .
A. 30° B. 45° C. 60° D. 150°
图 27-3
(5)下列关于三角形的外心的说法中 ,正确的是( ) .
A. 三角形的外心在三角形外
B. 三角形的外心到三边的距离相等
C. 三角形的外心到三个顶点的距离相等
D. 等腰三角形的外心在三角形内
(6)如图 27-4所示 ,一块边长为 8 cm 的正方形木板 ABCD,在水平桌面上绕点 A按逆时针方向旋转至 A'B'C'D'的位置 ,则顶点 C从开始到结束所经过的路径长为( ) .
图 27-4
A. 8π cm B. 4 2 cm C. 16 cm D. 16 2 cm
(7)如图 27-5所示 ,AB,AC与 ☉O 相 切 于 B,C 两 点 , ∠A= 50°,点 P 是 圆 上 异 于 B,C 的 一 动 点,则
∠BPC的度数为( ) .
A. 65° B. 115° C. 65°或 115° D. 130°或 50°
1
(8)如 图 27-6所 示 ,AB是 半 圆 的 直 径 ,AB= 2r,C, D 为 半 圆 的 三 等 分 点,则 图 中 阴 影 部 分 的 面 积
是( ) .
图 27-5 图 27-6
(9) “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题 : “今有圆材 ,埋在壁中 ,不知大小 , 以锯锯 之 ,深一寸 ,锯道长一尺 ,问经几何 ”用数学语句表述如下 :如图 27-7所示 ,CD为 ☉O的直径 , 弦 AB⊥CD于
点 E,CE= 1 寸 ,AB= 10寸 ,则直径 CD 的长为( ) .
A. 12.5 寸 B. 13寸 C. 25寸 D. 26寸
(10)如图 27-8所示 ,一把扇形纸扇完全打开后 ,外侧两竹条 AB,AC的夹角为 120°,AB长为30 cm ,贴 纸部分 BD 长为 20 cm ,则贴纸部分的面积为( ) .
A. 800π cm2 B. 500π cm2 C. π cm2 π cm2
图 27-7 图 27-8
2. 填空题(每题 3 分 ,共 30分)
(1)平面内到定点 P 的距离等于 4 cm 的所有点构成的图形是一个 .
(2)爆炸区 50 m 内 是 危 险 区 , 一 人 在 离 爆 炸 中 心 O 点 30 m 的 A 处 如 图 27-9 所 示 , 这 人 沿 射 线 的方向离开最快 ,离开 m 无危险 .
(3)如图 27-10所示 ,AB为 ☉O的直径 ,若 AB⊥EF于点 C,试填写一个你认为正确的结论 : .
图 27-9 图 27-10
(4)已知 ☉O的直径为 10 cm ,如果直线 L上的一点 P 到圆心 O的距离 5 cm ,那么直线 L与 ☉O的位置 关系是 .
(5)如图 27-11 所 示 , 有 一 圆 弧 形 门 拱 的 拱 高 AC 为 1 m , 跨 度 BD 为 4 m , 则 这 个 门 拱 的 半 径 为
m.
图 27-11
2
(6)如图 27-12所示 ,有一个圆锥形粮堆 ,其主视图是边长为 6 m 的等边三角形 ,母线的中点 P 有一只 老鼠正在偷吃粮食 ,小猫从 B处沿圆锥表面去偷袭老鼠 ,则小猫所经过的最短路径是 m. (结果不 取近似数)
(7)要用圆形铁片截出边长为 4 cm 的正方形铁片 ,则选用的圆形铁片的直径最小要 cm.
(8)如图 27-13所示 , ☉O的半径为 1, 圆周角 ∠ABC= 30°,则图中阴影部分的面积是 . (结果用 π表示)
(9)若过 ☉O内一点 P 的最长的弦长为 10 cm ,最短弦长为 8 cm ,则 OP 的长为 cm.
图 27-12 图 27-13
(10)如图 27-14所示 ,一段铁路弯道成圆弧形 , 圆弧的半径是 0. 3 km,一列火车以36km/h的速度用了 10 s通过弯道 ,那么弯道所对的圆心角的度数为 . ( π取 3.14,结果精确到 0.1°)
图 27-14
3. 解答题(共 40分)
(1)海中有一小岛 ,它周围 20 n mile有暗礁 ,一船跟踪鱼群由西向东航行 ,在点 B测得小岛 A 在北偏东 60°方向上 ,航行 30 n mile到达点 C,这时小岛A在北偏东 30°处 ,如果渔船不改变航向 ,继续向东追踪捕捞 , 有没有触礁的危险 (5分)
(2)如图 27-15所示 , ☉C经过原点且与两坐标轴分别交于 A,B 两点,点 A 的坐标为(0,4) ,M 是圆上
一点,∠BMO= 120°,求 ☉C的半径和圆心 C的坐标 . (5分)
图 27-15
3
(3)如图 27-16所示 ,有一块直径是 1 m 的圆形铁皮 ,要从中剪出一个最大的圆心角是 90°的扇形 ABC. (5分)
①求被剪掉的阴影部分的面积 ;
②用剪下的扇形铁皮围成一个圆锥 ,该圆锥的底面圆的半径是多少 (结果可用根号表示)
图 27-16
(4)如图 27-17所示 ,AB是 ☉O的直径 ,BD 是 ☉O的弦 ,延长 BD 到点 C,使 DC= BD,连接 AC交 ☉O 于点 E. (5分)
①AB与 AC的大小有什么关系
②按角的大小分类 ,请你判断 △ABC是属于哪一类三角形 ,并说明理由 .
图 27-17
(5)已知 △ABC内接于 ☉O,过点 A作直线 EF. (5分)
①如图 27-18(a)所示 ,AB为 ☉O的直径 ,要使得 EF是 ☉O的切线 ,还需添加的条件是(只需写 出 两种
即可) :A. ;B. .
②如图 27-18(b)所示 ,AB为非直径的弦 ,且 ∠CAE= ∠B. 求证 :EF是 ☉O的切线 .
(a) (b)
图 27-18
4
(6)如图 27-19所示 ,BE是 ☉O的直径 ,BC切 ☉O 于点 B, 弦 ED∥OC, 连接 CD 并延长交 BE 的延长 线于点 A. (5分)
①证明 :CD 是 ☉O的切线 ;
②若 AD= 2,AE= 1,求 CD 的长 .
图 27-19
(7)如图 27-20所示 ,在直角梯形 ABCD 中 ,AB∥CD, 以 AD为直径的圆切 BC 于点 E,连接 OB,OC, 试探究 OB与 OC 有何位置关系 (5分)
图 27-20
(8)如图 27-21所示,点 P 在 ☉O 外 ,PC是 ☉O的切线 ,C为切点,直线 PO 与 ☉O 相交于点 A,B. (5 分)
①试探求 ∠BCP与 ∠P 的数量关系 ;
②若 ∠A= 30°,则 PB与 PA 有什么数量关系
③∠A可能等于 45°吗 若 ∠A= 45°,则过点 C的切线与 AB有怎样的位置关系
④若 ∠A>45°,则过点 C的切线与直线 AB 的交点 P 的位置将在哪里
图 27-21
5
