华师大版(2024)数学七下7.1认识不等式(第2课时)课件(共23张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下7.1认识不等式(第2课时)课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
(华师大版)七年级
下
7.1认识不等式
(第2课时)
一元一次不等式
第7章
“七”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.能根据具体情境区别不等式的解与解集的意义.
2.能在数轴上表示不等式的解集,并且通过尝试把不等式的解集在数轴上表示出来,增强数形结合的意识.
新知导入
问题3:什么叫不等式的解?
问题2:常用的不等号有哪些?
问题1:什么叫不等式?
用不等号“>”“<”或“≥”“≤”表示不等关系的式子,叫做不等式.
>、<、≥、≤、≠
能使不等式成立的未知数的值,叫做不等式的解.
新知讲解
问题1:
下列各数中哪些是不等式x <-1的解?哪些不是?
-3,-2,-1,0,1.5,2.5,3,3.5,5,7.
除了上面提到的解外,你还能说出它的一些解吗?
x < -2
√
新知讲解
实际上,小于-2的每一个数都是不等式x<1的解,而不小于-2的每一个数都不是不等式 x<1的解.
可见不等式 x<1的解有无数个.
不等式 x<1 的解有无数个,它们组成一个集合,称为不等式x<1 的解集.
新知讲解
概括:
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.
注意
不等式的解集必须满足两个条件:
(1)解集中的任何一个数值都使不等式成立;
(2)解集外的任何一个数值都不能使不等式成立.
求不等式的解集的过程,叫做解不等式.
新知讲解
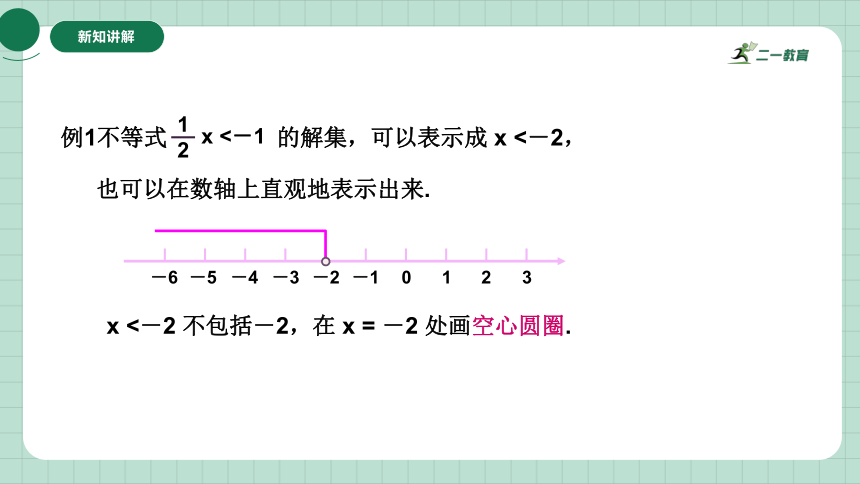
问题:
怎样表示不等式的解集呢?
用式子:
用最简形式的不等式(如 x>a 或 x用数轴:
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
新知讲解
x <-1
1
2
例1不等式 的解集,可以表示成 x <-2,
也可以在数轴上直观地表示出来.
-1
-2
0
1
2
3
-3
-4
-5
-6
x <-2 不包括-2,在 x = -2 处画空心圆圈.
新知讲解
例2 x + 2≥5 的解集,可以表示为 ________,
x≥3
用数轴表示为:
2
1
3
4
5
6
0
-1
-2
-3
x≥3 包括 3,在 x = 3 处画实心圆圈.
新知讲解
例1与例2的表示法有什么区别?
归纳:
在数轴上,解集x≤a,表示数a的点左边的部分,包括表示数a的点在内,这一点画成实心圆点;
而解集x对于解集x≥a和x>a在数轴上的表示,与此相仿.
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点
表示;不包含在解集中,则用空心点表示;
(3)定方向:相对于边界点,大于向右画,小于向左画.
新知讲解
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
【知识技能类作业】必做题:
课堂练习
1.下列说法正确的是( )
A.x = 5 是不等式 x+5>10 的解
B.x<5 是不等式 x5>0 的解集
C.x≥5 是不等式 x5≥0 的解集
D.x>3 是不等式 x3≥0 的解集
C
【知识技能类作业】必做题:
课堂练习
2.如图,数轴上表示的关于 的不等式的解集是______.
【知识技能类作业】必做题:
课堂练习
3. 把下列关系用不等式表示,并分别在数轴上表示出它们的解集:
(1) x小于-2;
(2) y不小于-3;
(3) x不是负数.
解:(1) x<-2 解集在数轴上的表示如图①所示
(2) y≥-3 解集在数轴上的表示如图②所示
(3) x≥0 解集在数轴上的表示如图③所示
【知识技能类作业】选做题:
课堂练习
4. 交通法规人人遵守,文明城市处处安全.通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志,则通过该桥洞的车高x(单位:m)的范围在数轴上可表示为( )
D
5.已知满足x【知识技能类作业】选做题:
课堂练习
5
6
【综合拓展类作业】
课堂练习
6. 借助数轴,试分别写出解集满足下列条件的一个不等式:
(1) 不等式的正整数解只有1、2、3、4;
(2) 不等式的解中不含0;
(3) 不等式的整数解只有-2、-1、0、1;
(4) -2、-1、0都是不等式的解.
解:答案不唯一,如(1) x<5 (2) x>2
(3) -3课堂总结
1.不等式的解集:
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.
不等式的解集必须满足两个条件:
(1)解集中的任何一个数值都使不等式成立;
(2)解集外的任何一个数值都不能使不等式成立.
2.解不等式:
求不等式的解集的过程,叫做解不等式.
课堂总结
3.用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点
表示;不包含在解集中,则用空心点表示;
(3)定方向:相对于边界点,大于向右画,小于向左画.
板书设计
1.不等式的解集:
2.解不等式:
课题:7.1认识不等式(第2课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
7.1认识不等式
(第2课时)
一元一次不等式
第7章
“七”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.能根据具体情境区别不等式的解与解集的意义.
2.能在数轴上表示不等式的解集,并且通过尝试把不等式的解集在数轴上表示出来,增强数形结合的意识.
新知导入
问题3:什么叫不等式的解?
问题2:常用的不等号有哪些?
问题1:什么叫不等式?
用不等号“>”“<”或“≥”“≤”表示不等关系的式子,叫做不等式.
>、<、≥、≤、≠
能使不等式成立的未知数的值,叫做不等式的解.
新知讲解
问题1:
下列各数中哪些是不等式x <-1的解?哪些不是?
-3,-2,-1,0,1.5,2.5,3,3.5,5,7.
除了上面提到的解外,你还能说出它的一些解吗?
x < -2
√
新知讲解
实际上,小于-2的每一个数都是不等式x<1的解,而不小于-2的每一个数都不是不等式 x<1的解.
可见不等式 x<1的解有无数个.
不等式 x<1 的解有无数个,它们组成一个集合,称为不等式x<1 的解集.
新知讲解
概括:
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.
注意
不等式的解集必须满足两个条件:
(1)解集中的任何一个数值都使不等式成立;
(2)解集外的任何一个数值都不能使不等式成立.
求不等式的解集的过程,叫做解不等式.
新知讲解
问题:
怎样表示不等式的解集呢?
用式子:
用最简形式的不等式(如 x>a 或 x
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
新知讲解
x <-1
1
2
例1不等式 的解集,可以表示成 x <-2,
也可以在数轴上直观地表示出来.
-1
-2
0
1
2
3
-3
-4
-5
-6
x <-2 不包括-2,在 x = -2 处画空心圆圈.
新知讲解
例2 x + 2≥5 的解集,可以表示为 ________,
x≥3
用数轴表示为:
2
1
3
4
5
6
0
-1
-2
-3
x≥3 包括 3,在 x = 3 处画实心圆圈.
新知讲解
例1与例2的表示法有什么区别?
归纳:
在数轴上,解集x≤a,表示数a的点左边的部分,包括表示数a的点在内,这一点画成实心圆点;
而解集x
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点
表示;不包含在解集中,则用空心点表示;
(3)定方向:相对于边界点,大于向右画,小于向左画.
新知讲解
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
【知识技能类作业】必做题:
课堂练习
1.下列说法正确的是( )
A.x = 5 是不等式 x+5>10 的解
B.x<5 是不等式 x5>0 的解集
C.x≥5 是不等式 x5≥0 的解集
D.x>3 是不等式 x3≥0 的解集
C
【知识技能类作业】必做题:
课堂练习
2.如图,数轴上表示的关于 的不等式的解集是______.
【知识技能类作业】必做题:
课堂练习
3. 把下列关系用不等式表示,并分别在数轴上表示出它们的解集:
(1) x小于-2;
(2) y不小于-3;
(3) x不是负数.
解:(1) x<-2 解集在数轴上的表示如图①所示
(2) y≥-3 解集在数轴上的表示如图②所示
(3) x≥0 解集在数轴上的表示如图③所示
【知识技能类作业】选做题:
课堂练习
4. 交通法规人人遵守,文明城市处处安全.通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志,则通过该桥洞的车高x(单位:m)的范围在数轴上可表示为( )
D
5.已知满足x
课堂练习
5
6
【综合拓展类作业】
课堂练习
6. 借助数轴,试分别写出解集满足下列条件的一个不等式:
(1) 不等式的正整数解只有1、2、3、4;
(2) 不等式的解中不含0;
(3) 不等式的整数解只有-2、-1、0、1;
(4) -2、-1、0都是不等式的解.
解:答案不唯一,如(1) x<5 (2) x>2
(3) -3
1.不等式的解集:
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.
不等式的解集必须满足两个条件:
(1)解集中的任何一个数值都使不等式成立;
(2)解集外的任何一个数值都不能使不等式成立.
2.解不等式:
求不等式的解集的过程,叫做解不等式.
课堂总结
3.用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点
表示;不包含在解集中,则用空心点表示;
(3)定方向:相对于边界点,大于向右画,小于向左画.
板书设计
1.不等式的解集:
2.解不等式:
课题:7.1认识不等式(第2课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
