15.1.2~3幂的乘方和积的乘方
文档属性
| 名称 | 15.1.2~3幂的乘方和积的乘方 |

|
|
| 格式 | rar | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-10 00:00:00 | ||
图片预览








文档简介
课件24张PPT。15.1.2~3幂的乘方和积的乘方
知识回顾 口述同底数幂的乘法法则am · an = am+n (m、n都是正整数).同底数幂相乘,底数不变,指数相加.(1) ; (3) ;(5) ;(6) .(2) ;(4) ;1.计算:复习与回顾3m3.根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
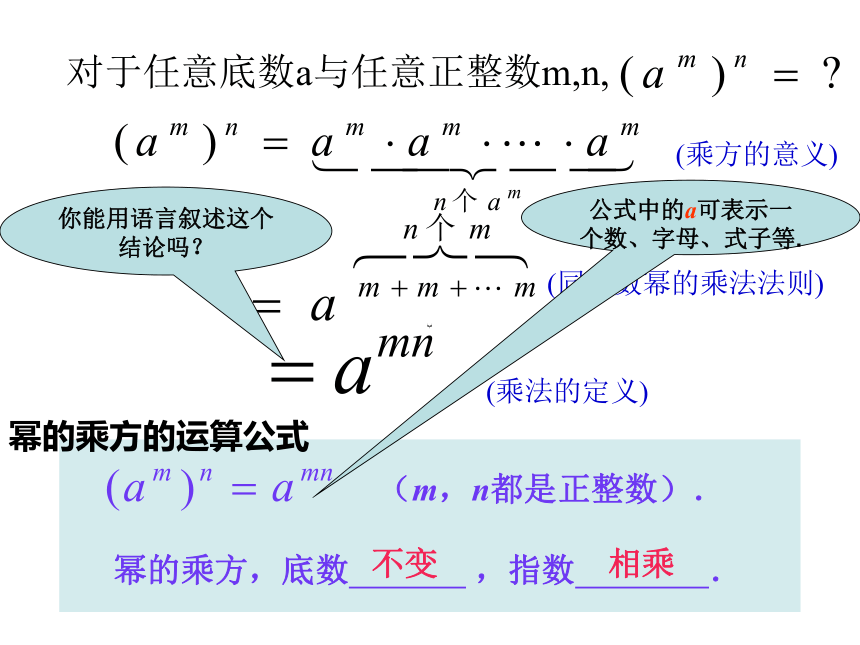
2.你发现了什么?66活动2 对于任意底数a与任意正整数m,n,(乘方的意义)(同底数幂的乘法法则)(乘法的定义)(m,n都是正整数).幂的乘方,底数 ,指数 .不变相乘幂的乘方的运算公式你能用语言叙述这个结论吗?公式中的a可表示一个数、字母、式子等.例2:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.解: (1) (103)5=103Χ5 = 1015 ; (2) (a4)4=a4Χ4=a16;
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .活动3 下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( ) × × × ×活动4 乘法乘方不变不变指数
相加指数
相乘活动5 相信你准能做对!计算:
(103)3; (2) (x3)2;
(3) - ( xm )5 ; (4) (a2 )3? a5;⑸⑹1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x · (x5)m (D) x · x5 · xmc2.x14不可以写成( )
(A)x5 · (x3)3 (B) (-x) · (-x2) · (-x3) · (-x8)
(C)(x7)7 (D)x3 · x4 · x5 · x2
C活动6 思考下面两道题:(1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算这两道题有什么特点?观察底数。底数为两个因式相乘,积的形式。这种形式为积的乘方我们学过的幂的乘方的运算性质适用吗?同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)分组讨论积的乘方有什么运算性质呢?根据以上做法口答:那么?n个n个n个 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(n为正整数)问题:结果是多少呢?结论:三个或三个以上的积的乘方也具有这一性质例3 计算:
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.解: (1) (2a)3=23?a3 = 8a3;
(2) (-5b)3=(-5)3?b3=-125b3;
(3) (xy2)2=x2?(y2)2=x2y4;
(4) (-2x3)4=(-2)4?(x3)4=16x12.练习
计算:
(ab)4 ; (2) (-2xy)3;
(3) (-3×102)3 ; (4) (2ab2)3. a4b4 ; (2) –8x3y3;
(3) –2.7×107; (4) 8a3b6.下列各题对吗?如果不对怎么更正?(1) ( 错 )(2)( 错 )(3)( 错 )(4)( 错 )应该是 应为应为应该为练习:2计算:解: (1)原式= (2)原式= 这两道题要注意确定符号,看负号是否参与乘方。这里我们把(x+y)看成是一个字母进行运算,这是常见的数学方法大家要掌握思维延伸1、已知,xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m?x2n; (3) x 3m+2n.解: (1) x m+n=x m?x n= ×3= ;
(2) x2m?x2n=(x m )2?(x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m?x2n=(x m)3?(x n)2=( )3×32
= × 9 = 2、计算:这题是不是直接算呢?有什么特点呢?*它是一个幂相乘的形式,能不能运用积的乘方运算性质呢?也就是把:逆用,先相乘后乘方解:(1)原式= (2)原式=同学们我们可以发现数学的形式很灵活,很生动,很优美 已知,44?83=2x,求x的值. 实践与创新解:1. 已知3×9n=37,求:n的值.2. 已知a3n=5,b2n=3,求:a6nb4n的值.3. 设n为正整数,且x2n=2,求9(x3n)2的值.
4. 已知2m=a,32n=b,求:23m+10n.实践与创新综合拓展通过计算比较下列各组中两个数的大小:
A 12____21; B 23_____32; C 34_____43;
D 45_____54; E 56_____65;……;
(2) 由题(1)的结果归纳猜想出n n+1和(n+1)n的大小关系是_________;
(3) 根据上面的结论比较20042005和20052004大小关系是________.
知识回顾 口述同底数幂的乘法法则am · an = am+n (m、n都是正整数).同底数幂相乘,底数不变,指数相加.(1) ; (3) ;(5) ;(6) .(2) ;(4) ;1.计算:复习与回顾3m3.根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
2.你发现了什么?66活动2 对于任意底数a与任意正整数m,n,(乘方的意义)(同底数幂的乘法法则)(乘法的定义)(m,n都是正整数).幂的乘方,底数 ,指数 .不变相乘幂的乘方的运算公式你能用语言叙述这个结论吗?公式中的a可表示一个数、字母、式子等.例2:计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) -(x4)3.解: (1) (103)5=103Χ5 = 1015 ; (2) (a4)4=a4Χ4=a16;
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .活动3 下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( ) × × × ×活动4 乘法乘方不变不变指数
相加指数
相乘活动5 相信你准能做对!计算:
(103)3; (2) (x3)2;
(3) - ( xm )5 ; (4) (a2 )3? a5;⑸⑹1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x · (x5)m (D) x · x5 · xmc2.x14不可以写成( )
(A)x5 · (x3)3 (B) (-x) · (-x2) · (-x3) · (-x8)
(C)(x7)7 (D)x3 · x4 · x5 · x2
C活动6 思考下面两道题:(1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算这两道题有什么特点?观察底数。底数为两个因式相乘,积的形式。这种形式为积的乘方我们学过的幂的乘方的运算性质适用吗?同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)分组讨论积的乘方有什么运算性质呢?根据以上做法口答:那么?n个n个n个 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(n为正整数)问题:结果是多少呢?结论:三个或三个以上的积的乘方也具有这一性质例3 计算:
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.解: (1) (2a)3=23?a3 = 8a3;
(2) (-5b)3=(-5)3?b3=-125b3;
(3) (xy2)2=x2?(y2)2=x2y4;
(4) (-2x3)4=(-2)4?(x3)4=16x12.练习
计算:
(ab)4 ; (2) (-2xy)3;
(3) (-3×102)3 ; (4) (2ab2)3. a4b4 ; (2) –8x3y3;
(3) –2.7×107; (4) 8a3b6.下列各题对吗?如果不对怎么更正?(1) ( 错 )(2)( 错 )(3)( 错 )(4)( 错 )应该是 应为应为应该为练习:2计算:解: (1)原式= (2)原式= 这两道题要注意确定符号,看负号是否参与乘方。这里我们把(x+y)看成是一个字母进行运算,这是常见的数学方法大家要掌握思维延伸1、已知,xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m?x2n; (3) x 3m+2n.解: (1) x m+n=x m?x n= ×3= ;
(2) x2m?x2n=(x m )2?(x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m?x2n=(x m)3?(x n)2=( )3×32
= × 9 = 2、计算:这题是不是直接算呢?有什么特点呢?*它是一个幂相乘的形式,能不能运用积的乘方运算性质呢?也就是把:逆用,先相乘后乘方解:(1)原式= (2)原式=同学们我们可以发现数学的形式很灵活,很生动,很优美 已知,44?83=2x,求x的值. 实践与创新解:1. 已知3×9n=37,求:n的值.2. 已知a3n=5,b2n=3,求:a6nb4n的值.3. 设n为正整数,且x2n=2,求9(x3n)2的值.
4. 已知2m=a,32n=b,求:23m+10n.实践与创新综合拓展通过计算比较下列各组中两个数的大小:
A 12____21; B 23_____32; C 34_____43;
D 45_____54; E 56_____65;……;
(2) 由题(1)的结果归纳猜想出n n+1和(n+1)n的大小关系是_________;
(3) 根据上面的结论比较20042005和20052004大小关系是________.
