1.3简单的逻辑联结词
图片预览











文档简介
课件36张PPT。1.3 简单的逻辑联结词共2课时 日常生活用语中如果说“哥哥的年龄比我大或我的年龄比哥哥大”、“萝卜长在土地里或长在树上”肯定不妥,但数学语言3>4或4>3却是正确的,这究竟是为什么呢?逻辑联结词(1)不等式 的解集是 ;
(2)不等式 的解集是 ;
(3) 不是方程 的根。逻辑联结词例1 判断下面的语句是否为命题?若是命题,指出它的真假。我们再来看几个复杂的命题:(1)10可以被2或5整除.(2)菱形的对角线互相垂直且平分.(3)0.5非整数. “或”,“且”, “非”称为逻辑联结词.含有逻辑联结词的命题称为复合命题,不含逻辑联结词的命题称为简单命题.简 单 命 题:不含逻辑联结词的命题复 合 命 题:由简单命题和逻辑联结词
构成的命题(常用小写字母p,q,r,s,……表示)复合命题有以下三种形式:(1)P且q.
(2)P或q.
(3)非p. 一般地,用逻辑联结词”或”把命题p和命题q联结起来.就得到一个新命题,记作 读作”p或q”.(1)10可以被2或5整除p: 10可以被2整除q: 10可以被5整除p或q:10可以被2整除或被5整除规定:当p,q两个命题中有一个是真命题
时, 是真命题;当p,q两个命题中都是
假命题时, 是假命题.pq同假为假,一真为真. 一般地,用逻辑联结词”且”把命题p和命题q联结起来.就得到一个新命题,记作
读作”p且q”.(2)菱形的对角线互相垂直且平分p: 菱形的对角线互相垂直q: 菱形的对角线互相平分p且q:菱形的对角线互相垂直且互相平分
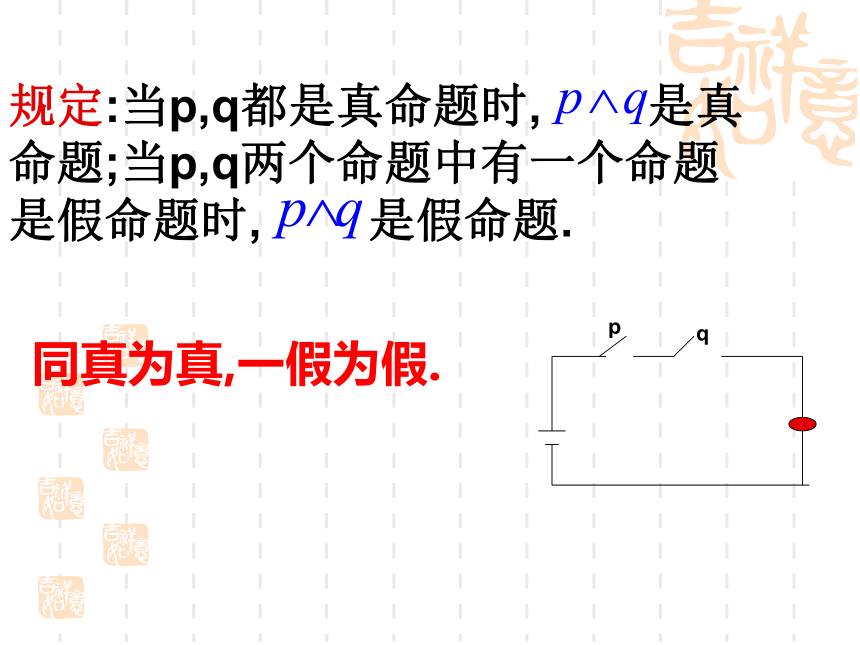
规定:当p,q都是真命题时, 是真命题;当p,q两个命题中有一个命题是假命题时, 是假命题.同真为真,一假为假.pq(3)0.5非整数p: 0.5是整数非p: 0.5非整数 一般地,对一个命题p全盘否定,就得到一个新命题,记作
读作”非p”或”p的否定”真假相反.例1:指出下列命题的构成形式及构成它的简单命题:(1)24 既是 8 的倍数也是 6 的倍数(2)小李是篮球运动员或跳高运动员(3)平行线不相交(4)小张是学生,小王也是学生p且qp或q非pp且qp:24既是3的倍数q:24是6的倍数p:小李是篮球运动员q:小李是跳高运动员p:平行线相交p:小张是学生q:小王是学生例2: 分别指出下列复合命题的形式(1)8≥7;
(2)2≤x<5;
(3) a≠4 ;
(4) π不是整数. 例3 分别写出由命题
“p:平行四边形的对角线相等”,
“q:平行四边形的对角线互相平分”
构成的“P或q”,“P且q”,“非p”形式的命题。1、P∨q的否定形式为:┒P或┒q2、P∧q的否定形式为:┒P且┒q例4:写出下列命题的非命题:(2)-1是偶数或奇数;(1)不等式 的解集是 ;
(2)不等式 的解集是 ;
(3) 不是方程 的根。本节须注意的几个方面:(1)“≥”的意义是“>或=”.(2)“非”命题对常见的几个正面词语的否定.注意
逻辑联结词中的”或”相当于集合中的”并集”,它与日常用语中的”或”的含义不同.日常用语中的”或”是两个中任选一个,不能都选,而逻辑联结词中的”或”,可以是两个都选,但又不是两个都选,而是两个中至少选一个,因此,有三种可能的情况.
逻辑联结词中的”且”相当于集合中的”交集”,即两个必须都选.例3:写出下列命题的非命题:(1)p:对任意实数x,均有x2-2x+1≥0;(2)q:存在一个实数x,使得x2-9=0;(3)“AB∥CD”且“AB=CD”;(4)“△ABC是直角三角形或等腰三角形”.1.3 简单的逻辑联结词第2课时简 单 命 题:不含逻辑联结词的命题复 合 命 题:由简单命题和逻辑联结词
构成的命题(常用小写字母p,q,r,s,……表示)复合命题有以下三种形式:(1) P或q
(2) P且q
(3) 非p概念(1) P或q
(2) P且q
(3) 非p同假为假,一真为真.同真为真,一假为假.真假相反.真假判定问题1: 判断下列复合命题的真假:(2)2是偶数且2是质数;(3)π不是整数;(1) 8≥7 ;“非p”形式的复合命题真假: 例1:写出下列命题的非,并判断真假:
(1)p:方程x2+1=0有实数根
(2)p:3<2
(3)p: 2+2=5
(4)p:等腰三角形两底角相等当p为真时,非p为假;
当p为假时,非p为真. “p且q”形式的复合命题真假: 例2:判断下列命题的真假:
(1)正方形ABCD是矩形,且是菱形;
(2)5是10的约数且是15的约数
(3)5是10的约数且是8的约数
(4)x2-5x=0的根是自然数当p、q为真时,p且q为真;
当p、q中至少有一个为假时,p且q为假。 “p或q”形式的复合命题真假: 例3:判断下列命题的真假:
(1)5是10的约数或是15的约数;
(2)5是12的约数或是8的约数;
(3)5是12的约数或是15的约数;
(4)方程x2-3x-4=0的判别式大于或等于零当p、q中至少有一个为真时,p或q为真;
当p、q都为假时,p或q为假。非p形式复合命题p且q形式复合命题P或q形式复合命题真值表假假假假假真真真真真(1) P或q
(2) P且q
(3) 非p同假为假,一真为真.同真为真,一假为假.真假相反.真假判定例1.分别指出由下列各组命题构成的p或q、p且q、非p形式的复合命题的真假:(1)p:2+2=5q:3>2 (2)p:9是质数q:8是12的约数(3)p:1∈{1,2} 解:(1) 因为p假q真 所以
“ p或q”为真 , “p且q”为假 ,“非p”为真 (2) 因为p假q假 所以
“p或q”为假 , “p且q”为假 ,“非p”为真(3) 因为p真q真 所以
“p 或q”为真 , “p且q”为真 ,“非p”为假(4) 因为p真q假 所以
“p 或q”为真 , “p且q”为假 ,“非p”为假判断复合命题真假的步骤:(1)写出构成复合命题的简单命题p与q(2)判断p 、q的真假(3)由真值表判断复合命题真假例2.判断下列命题的真假: (2)3≥3(1)4>3>2 (3)对一切实数解:(2)p:3>3,假;q:3=3,真;p或q为真(1)p:3>2,真;q:3<4,真;p且q为真(3)p:对一切实数 ,真;
q:对一切实数 ,假;
p或q为真P或qP或qP且q例3.判断下列命题的真假: (1)4≥3
(2)4≥4
(3)4≥5例4、判斷下列P∨q、 P∧q、┒p命題形式的真假﹔(2)、-1是偶数或奇数;提醒:1、P∨q的否定形式为:┒P或┒q ┒P且 ┒q为真命题,即P假q假2、P∧q的否定形式为:┒P且┒q3、P∨ q的否定形式为真命题,则p,q的真假是:4、若P∨ q是真命题, P∧q是假命题,则p,q的真假是:P真q假 或 P假q真5、若P∧q是真命题,则
P或┒q是真命题 ② P且┒q是真命题
③ ┒P且┒q是假命题 ④ ┒P或q是假命题
其中正确的是_______ ①③归纳总结简
单
的
逻
辑
联
结
词1、简单命题与复合命题3、注意逻辑联结与普通联结词的区分2、复合命題的真假﹔
(2)不等式 的解集是 ;
(3) 不是方程 的根。逻辑联结词例1 判断下面的语句是否为命题?若是命题,指出它的真假。我们再来看几个复杂的命题:(1)10可以被2或5整除.(2)菱形的对角线互相垂直且平分.(3)0.5非整数. “或”,“且”, “非”称为逻辑联结词.含有逻辑联结词的命题称为复合命题,不含逻辑联结词的命题称为简单命题.简 单 命 题:不含逻辑联结词的命题复 合 命 题:由简单命题和逻辑联结词
构成的命题(常用小写字母p,q,r,s,……表示)复合命题有以下三种形式:(1)P且q.
(2)P或q.
(3)非p. 一般地,用逻辑联结词”或”把命题p和命题q联结起来.就得到一个新命题,记作 读作”p或q”.(1)10可以被2或5整除p: 10可以被2整除q: 10可以被5整除p或q:10可以被2整除或被5整除规定:当p,q两个命题中有一个是真命题
时, 是真命题;当p,q两个命题中都是
假命题时, 是假命题.pq同假为假,一真为真. 一般地,用逻辑联结词”且”把命题p和命题q联结起来.就得到一个新命题,记作
读作”p且q”.(2)菱形的对角线互相垂直且平分p: 菱形的对角线互相垂直q: 菱形的对角线互相平分p且q:菱形的对角线互相垂直且互相平分
规定:当p,q都是真命题时, 是真命题;当p,q两个命题中有一个命题是假命题时, 是假命题.同真为真,一假为假.pq(3)0.5非整数p: 0.5是整数非p: 0.5非整数 一般地,对一个命题p全盘否定,就得到一个新命题,记作
读作”非p”或”p的否定”真假相反.例1:指出下列命题的构成形式及构成它的简单命题:(1)24 既是 8 的倍数也是 6 的倍数(2)小李是篮球运动员或跳高运动员(3)平行线不相交(4)小张是学生,小王也是学生p且qp或q非pp且qp:24既是3的倍数q:24是6的倍数p:小李是篮球运动员q:小李是跳高运动员p:平行线相交p:小张是学生q:小王是学生例2: 分别指出下列复合命题的形式(1)8≥7;
(2)2≤x<5;
(3) a≠4 ;
(4) π不是整数. 例3 分别写出由命题
“p:平行四边形的对角线相等”,
“q:平行四边形的对角线互相平分”
构成的“P或q”,“P且q”,“非p”形式的命题。1、P∨q的否定形式为:┒P或┒q2、P∧q的否定形式为:┒P且┒q例4:写出下列命题的非命题:(2)-1是偶数或奇数;(1)不等式 的解集是 ;
(2)不等式 的解集是 ;
(3) 不是方程 的根。本节须注意的几个方面:(1)“≥”的意义是“>或=”.(2)“非”命题对常见的几个正面词语的否定.注意
逻辑联结词中的”或”相当于集合中的”并集”,它与日常用语中的”或”的含义不同.日常用语中的”或”是两个中任选一个,不能都选,而逻辑联结词中的”或”,可以是两个都选,但又不是两个都选,而是两个中至少选一个,因此,有三种可能的情况.
逻辑联结词中的”且”相当于集合中的”交集”,即两个必须都选.例3:写出下列命题的非命题:(1)p:对任意实数x,均有x2-2x+1≥0;(2)q:存在一个实数x,使得x2-9=0;(3)“AB∥CD”且“AB=CD”;(4)“△ABC是直角三角形或等腰三角形”.1.3 简单的逻辑联结词第2课时简 单 命 题:不含逻辑联结词的命题复 合 命 题:由简单命题和逻辑联结词
构成的命题(常用小写字母p,q,r,s,……表示)复合命题有以下三种形式:(1) P或q
(2) P且q
(3) 非p概念(1) P或q
(2) P且q
(3) 非p同假为假,一真为真.同真为真,一假为假.真假相反.真假判定问题1: 判断下列复合命题的真假:(2)2是偶数且2是质数;(3)π不是整数;(1) 8≥7 ;“非p”形式的复合命题真假: 例1:写出下列命题的非,并判断真假:
(1)p:方程x2+1=0有实数根
(2)p:3<2
(3)p: 2+2=5
(4)p:等腰三角形两底角相等当p为真时,非p为假;
当p为假时,非p为真. “p且q”形式的复合命题真假: 例2:判断下列命题的真假:
(1)正方形ABCD是矩形,且是菱形;
(2)5是10的约数且是15的约数
(3)5是10的约数且是8的约数
(4)x2-5x=0的根是自然数当p、q为真时,p且q为真;
当p、q中至少有一个为假时,p且q为假。 “p或q”形式的复合命题真假: 例3:判断下列命题的真假:
(1)5是10的约数或是15的约数;
(2)5是12的约数或是8的约数;
(3)5是12的约数或是15的约数;
(4)方程x2-3x-4=0的判别式大于或等于零当p、q中至少有一个为真时,p或q为真;
当p、q都为假时,p或q为假。非p形式复合命题p且q形式复合命题P或q形式复合命题真值表假假假假假真真真真真(1) P或q
(2) P且q
(3) 非p同假为假,一真为真.同真为真,一假为假.真假相反.真假判定例1.分别指出由下列各组命题构成的p或q、p且q、非p形式的复合命题的真假:(1)p:2+2=5q:3>2 (2)p:9是质数q:8是12的约数(3)p:1∈{1,2} 解:(1) 因为p假q真 所以
“ p或q”为真 , “p且q”为假 ,“非p”为真 (2) 因为p假q假 所以
“p或q”为假 , “p且q”为假 ,“非p”为真(3) 因为p真q真 所以
“p 或q”为真 , “p且q”为真 ,“非p”为假(4) 因为p真q假 所以
“p 或q”为真 , “p且q”为假 ,“非p”为假判断复合命题真假的步骤:(1)写出构成复合命题的简单命题p与q(2)判断p 、q的真假(3)由真值表判断复合命题真假例2.判断下列命题的真假: (2)3≥3(1)4>3>2 (3)对一切实数解:(2)p:3>3,假;q:3=3,真;p或q为真(1)p:3>2,真;q:3<4,真;p且q为真(3)p:对一切实数 ,真;
q:对一切实数 ,假;
p或q为真P或qP或qP且q例3.判断下列命题的真假: (1)4≥3
(2)4≥4
(3)4≥5例4、判斷下列P∨q、 P∧q、┒p命題形式的真假﹔(2)、-1是偶数或奇数;提醒:1、P∨q的否定形式为:┒P或┒q ┒P且 ┒q为真命题,即P假q假2、P∧q的否定形式为:┒P且┒q3、P∨ q的否定形式为真命题,则p,q的真假是:4、若P∨ q是真命题, P∧q是假命题,则p,q的真假是:P真q假 或 P假q真5、若P∧q是真命题,则
P或┒q是真命题 ② P且┒q是真命题
③ ┒P且┒q是假命题 ④ ┒P或q是假命题
其中正确的是_______ ①③归纳总结简
单
的
逻
辑
联
结
词1、简单命题与复合命题3、注意逻辑联结与普通联结词的区分2、复合命題的真假﹔
