北师大八下2.6.1一元一次不等式组(1)
文档属性
| 名称 | 北师大八下2.6.1一元一次不等式组(1) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 16:09:47 | ||
图片预览








文档简介
(共27张PPT)
第二章 一元一次不等式及一元一次不等式组
2.6.1一元一次不等式组(1)
北师大版 数学 八年级 下册
学习目标
1.理解一元一次不等式组及不等式组的解集的概念;
2.会利用数轴求不等式组的解集;
3.能够正确地解出不等式组的解集.
情景导入
解下列一元一次不等式,并在数轴上表示它们的解集:
① 2x-3<6-x ; ②1-4x≤5x-2.
解: ①移项、合并同类项,得3x <9.
两边都除以3,得x <3.
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
情景导入
解下列一元一次不等式,并在数轴上表示它们的解集:
① 2x-3<6-x ; ②1-4x≤5x-2.
解: ②移项、合并同类项,得-9x ≤ -3.
两边都除以-9,得
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
情景导入
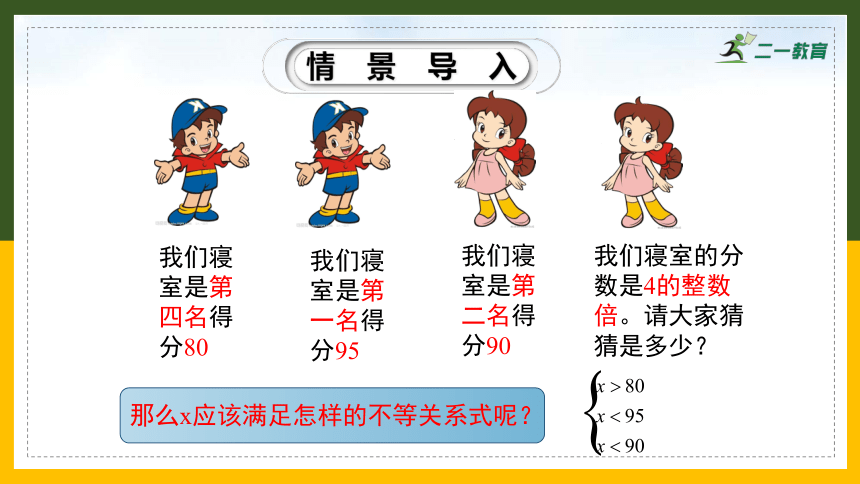
我们寝室是第二名得分90
我们寝室是第一名得分95
我们寝室是第四名得分80
我们寝室的分数是4的整数倍。请大家猜猜是多少?
那么x应该满足怎样的不等关系式呢?
核心知识点一:
一元一次不等式组的概念及解集
某校今年冬季烧煤取暖时间为4个月. 如果每月比计划多烧5t煤,那么取暖用煤总量将超过100t;如果每月比计划少烧5t煤,那么取暖用煤总量不足68t. 若该校计划每月烧煤xt,则x满足怎样的关系式?
分析:题中都有哪些不等关系呢?
1.如果每月比计划多烧5t煤,那么取暖用煤总量将超过100t.
2.如果每月比计划少烧5t煤,那么取暖用煤总量不足68t.
探索新知
根据题意得:
4(x+5)>100, ①
4(x-5)<68. ②
未知数x同时满足①②两个条件,把①②两个不等式合在一起
4(x+5)>100,
4(x-5)<68.
这个式子有什么特点?
探索新知
归纳总结
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
特点:
(1)每个不等式必须为一元一次不等式;
(2)所有不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个.
探索新知
练一练:下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
探索新知
核心知识点二:
解一元一次不等式组
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(1)现配制这种饮料10 kg,要求至少含有4 200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
600x+100(10-x) ≥ 4200
探索新知
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(kg)应满足的另一个不等式吗?
8x+4(10-x)≤72
探索新知
如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
探索新知
你能尝试找出下面一元一次不等式组中的未知数的值吗?
解不等式4(x+5)>100得:
x> 20
解不等式4(x-5)<68得:
x<22
在数轴上表示解集为:
17 18 19 20 21 22 23 24 25
在数轴上表示解集为:
17 18 19 20 21 22 23 24 25
4(x+5)>100,
4(x-5)<68.
探索新知
你能将上面两个解集表示在同一个数轴上吗?
17 18 19 20 21 22 23 24 25
公共部分
解集为:20探索新知
归纳总结
一元一次不等式组中各个不等式解集的公共部分,叫做不等式组的解集.
求不等式组的解集的过程叫做解不等式组。
注: 当它们没有公共部分时,则称这个不等式组无解.
探索新知
思考:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无解了
x>b
xa无解
探索新知
例: 解不等式组:
解不等式②,得
把不等式①、②的解集在数轴上表示出来,如图:
解: 解不等式①,得
因此,原不等式组的解集为
3
0
6
探索新知
例:解不等式组:
①
②
解: 解不等式①,得
解不等式②,得
x <-3.
x ≤ 3.
在同一数轴上表示不等式①②的解集如下:
∴这个不等式组的解集是 x<-3.
0
-3
3
○
●
探索新知
你能总结一下解一元一次不等式组的方法步骤吗?
(1)求各个不等式的解集;
(2)在同一数轴上表示出各个不等式的解集并找出这些不等式解集的公共部分;
(3)写出不等式组的解集.
归纳总结
探索新知
当堂检测
1.下列各式中是一元一次不等式组的是( )
A
当堂检测
A.x>-1 B.x<3
C.x<-1或x>3 D.-1<x<3
D
C
当堂检测
A.8 B.6
C.5 D.4
C
当堂检测
6.解下列不等式组:
解:(1)-3<x<3.
解:(2)1<x≤4.
x<2
当堂检测
解:解不等式①,得x≤1,
解不等式②,得x>-1,
不等式①②的解集在数轴上表示如图所示:
∴不等式组的解集为-1<x≤1.
当堂检测
8.某超市销售一批创意闹钟,先以55元/个的价格售出60个,然后调低价格,以50元/个的价格将剩下的闹钟全部售出,销售总额超过了5 500元,这批闹钟至少有个?
解:设这批创意闹钟有x个,根据题意,
得55×60+(x-60)×50>5 500,
解得x>104,
∴这批创意闹钟至少有105个.
1.一元一次不等式组中各个不等式的解集的公共部分,
叫做这个一元一次不等式组的解集.
求不等式组解集的过程,叫做解不等式组.
2.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
③表示这个不等式组的解集.
②利用数轴求出这些不等式解集的公共部分.
感谢收看
第二章 一元一次不等式及一元一次不等式组
2.6.1一元一次不等式组(1)
北师大版 数学 八年级 下册
学习目标
1.理解一元一次不等式组及不等式组的解集的概念;
2.会利用数轴求不等式组的解集;
3.能够正确地解出不等式组的解集.
情景导入
解下列一元一次不等式,并在数轴上表示它们的解集:
① 2x-3<6-x ; ②1-4x≤5x-2.
解: ①移项、合并同类项,得3x <9.
两边都除以3,得x <3.
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
情景导入
解下列一元一次不等式,并在数轴上表示它们的解集:
① 2x-3<6-x ; ②1-4x≤5x-2.
解: ②移项、合并同类项,得-9x ≤ -3.
两边都除以-9,得
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
情景导入
我们寝室是第二名得分90
我们寝室是第一名得分95
我们寝室是第四名得分80
我们寝室的分数是4的整数倍。请大家猜猜是多少?
那么x应该满足怎样的不等关系式呢?
核心知识点一:
一元一次不等式组的概念及解集
某校今年冬季烧煤取暖时间为4个月. 如果每月比计划多烧5t煤,那么取暖用煤总量将超过100t;如果每月比计划少烧5t煤,那么取暖用煤总量不足68t. 若该校计划每月烧煤xt,则x满足怎样的关系式?
分析:题中都有哪些不等关系呢?
1.如果每月比计划多烧5t煤,那么取暖用煤总量将超过100t.
2.如果每月比计划少烧5t煤,那么取暖用煤总量不足68t.
探索新知
根据题意得:
4(x+5)>100, ①
4(x-5)<68. ②
未知数x同时满足①②两个条件,把①②两个不等式合在一起
4(x+5)>100,
4(x-5)<68.
这个式子有什么特点?
探索新知
归纳总结
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
特点:
(1)每个不等式必须为一元一次不等式;
(2)所有不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个.
探索新知
练一练:下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
探索新知
核心知识点二:
解一元一次不等式组
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(1)现配制这种饮料10 kg,要求至少含有4 200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
600x+100(10-x) ≥ 4200
探索新知
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(kg)应满足的另一个不等式吗?
8x+4(10-x)≤72
探索新知
如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
探索新知
你能尝试找出下面一元一次不等式组中的未知数的值吗?
解不等式4(x+5)>100得:
x> 20
解不等式4(x-5)<68得:
x<22
在数轴上表示解集为:
17 18 19 20 21 22 23 24 25
在数轴上表示解集为:
17 18 19 20 21 22 23 24 25
4(x+5)>100,
4(x-5)<68.
探索新知
你能将上面两个解集表示在同一个数轴上吗?
17 18 19 20 21 22 23 24 25
公共部分
解集为:20
归纳总结
一元一次不等式组中各个不等式解集的公共部分,叫做不等式组的解集.
求不等式组的解集的过程叫做解不等式组。
注: 当它们没有公共部分时,则称这个不等式组无解.
探索新知
思考:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无解了
x>b
x
探索新知
例: 解不等式组:
解不等式②,得
把不等式①、②的解集在数轴上表示出来,如图:
解: 解不等式①,得
因此,原不等式组的解集为
3
0
6
探索新知
例:解不等式组:
①
②
解: 解不等式①,得
解不等式②,得
x <-3.
x ≤ 3.
在同一数轴上表示不等式①②的解集如下:
∴这个不等式组的解集是 x<-3.
0
-3
3
○
●
探索新知
你能总结一下解一元一次不等式组的方法步骤吗?
(1)求各个不等式的解集;
(2)在同一数轴上表示出各个不等式的解集并找出这些不等式解集的公共部分;
(3)写出不等式组的解集.
归纳总结
探索新知
当堂检测
1.下列各式中是一元一次不等式组的是( )
A
当堂检测
A.x>-1 B.x<3
C.x<-1或x>3 D.-1<x<3
D
C
当堂检测
A.8 B.6
C.5 D.4
C
当堂检测
6.解下列不等式组:
解:(1)-3<x<3.
解:(2)1<x≤4.
x<2
当堂检测
解:解不等式①,得x≤1,
解不等式②,得x>-1,
不等式①②的解集在数轴上表示如图所示:
∴不等式组的解集为-1<x≤1.
当堂检测
8.某超市销售一批创意闹钟,先以55元/个的价格售出60个,然后调低价格,以50元/个的价格将剩下的闹钟全部售出,销售总额超过了5 500元,这批闹钟至少有个?
解:设这批创意闹钟有x个,根据题意,
得55×60+(x-60)×50>5 500,
解得x>104,
∴这批创意闹钟至少有105个.
1.一元一次不等式组中各个不等式的解集的公共部分,
叫做这个一元一次不等式组的解集.
求不等式组解集的过程,叫做解不等式组.
2.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
③表示这个不等式组的解集.
②利用数轴求出这些不等式解集的公共部分.
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
