1.2充要条件

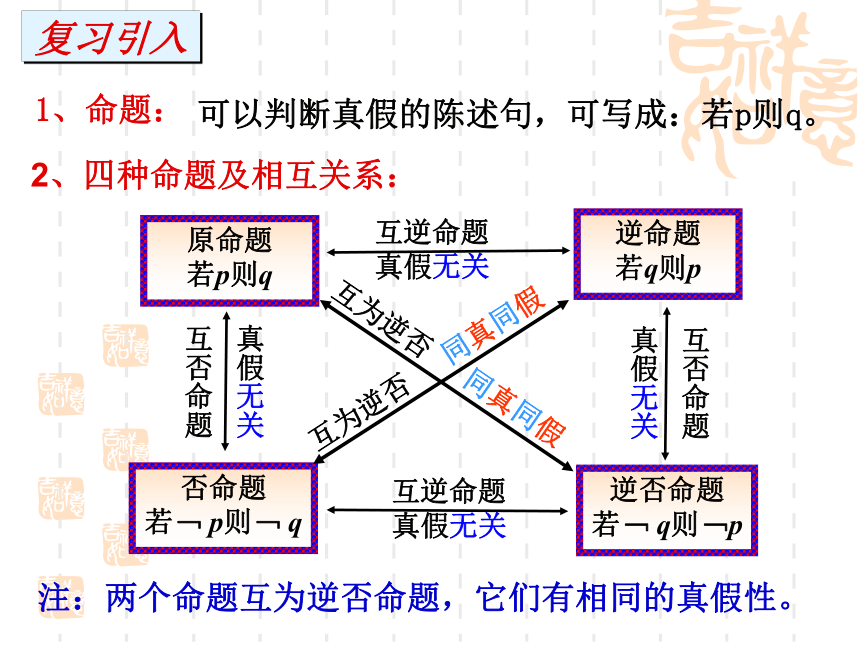
课件36张PPT。1.2 充要条件共2课时1、命题：可以判断真假的陈述句，可写成：若p则q。 2、四种命题及相互关系：复习引入注：两个命题互为逆否命题，它们有相同的真假性。互为逆否 同真同假互为逆否 同真同假互逆命题
真假无关互逆命题
真假无关真假无关
互否命题互否命题
真假无关推断符号“ ”的含义 如果命题“若p则q”为真，则记作p q
（或q p）。判断下列命题是真命题还是假命题： （3）对角线互相垂直的四边形是菱形； 真 假 假 假 真 (6) 若两三角形全等 ，则两三角形面积相等；
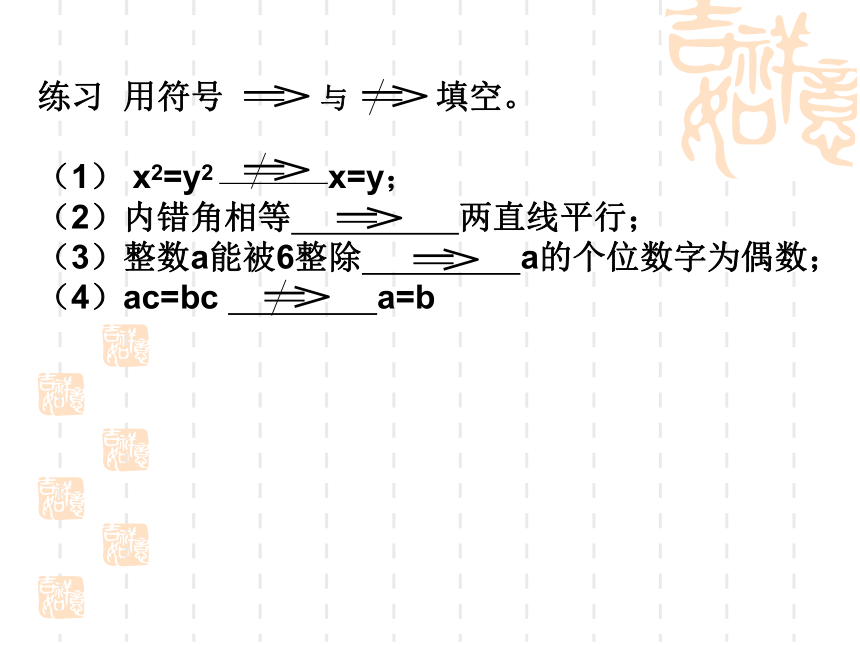
真练习 用符号 与 填空。 （1） x2=y2 x=y；（2）内错角相等 两直线平行；（3）整数a能被6整除 a的个位数字为偶数；（4）ac=bc a=b 定义：两三角形全等是两三角形面积相等的充分条件．两三角形面积相等是两三角形全等的必要条件．a = 0 ab=0。
要使结论ab=0成立，只要有条件a =0就足够了，“足够”就是“充分”的意思，因此称a =0是ab=0的充分条件。另一方面要使a =0，必须具备ab=0的条件，因此我们称ab=0是a =0的必要条件。
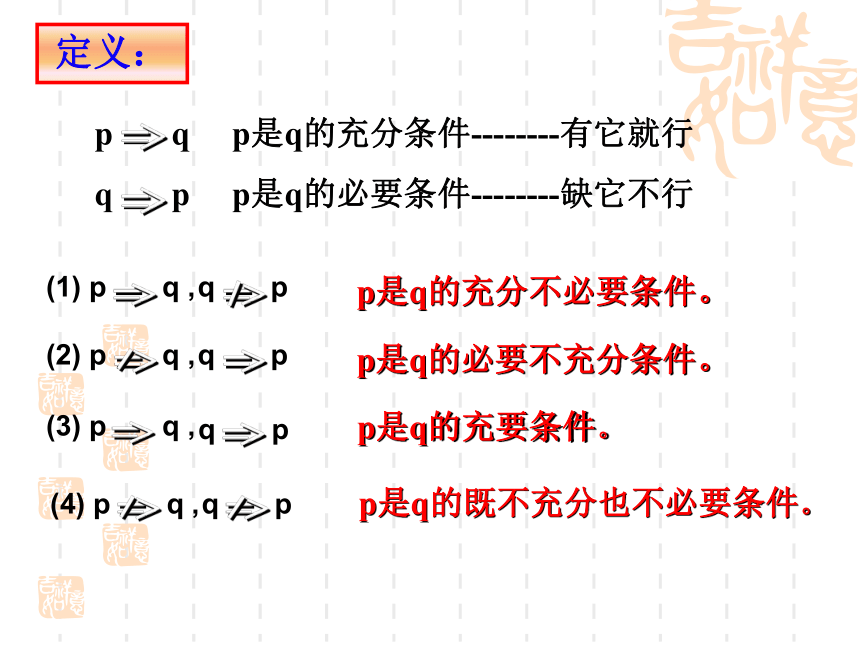
例1 ．指出下列各组命题中，p是q的什么条件 , q q是p的什么条件.p是q的必要条件。p是q的充分条件。p是q的充分条件。p是q的必要条件。p是q的充分条件。p是q的充分条件。p是q的必要条件。P不是q的充分条件或必要条件。p是q的充分不必要条件。p是q的充要条件。p是q的必要不充分条件。p是q的既不充分也不必要条件。定义：1、充分不必要条件
2、必要不充分条件
3、充分且必要条件
4、既不充分也不必要条件
各种条件的可能情况（充要条件） 例2、以“充分不必要条件”、“必要不充分条件”、“充
要条件”与”既不充分也不必要条件“中选出适当的一种
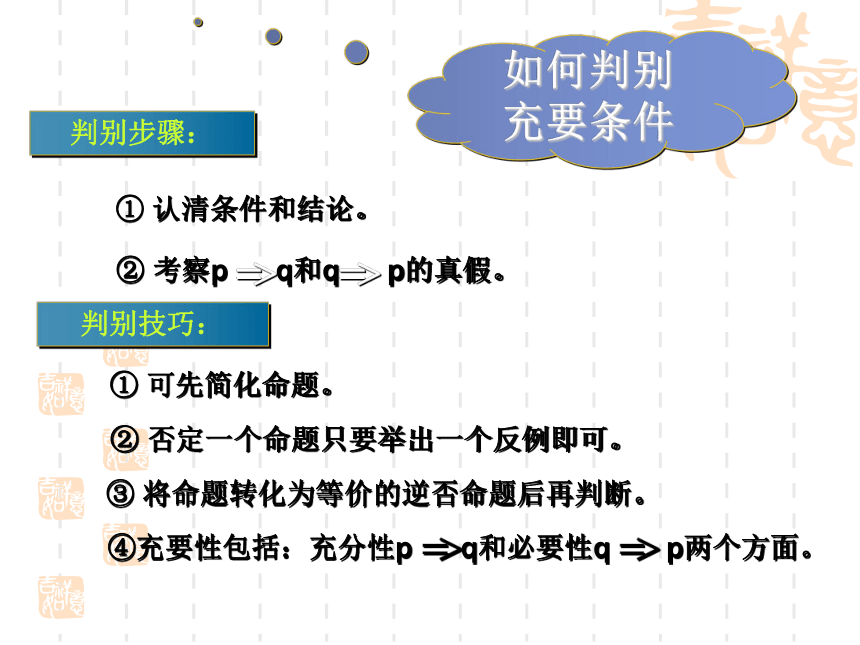
填空.（充分不必要条件）（充分不必要条件）（必要不充分条件）（必要不充分条件）（充要条件）（充要条件）（既不充分也不必要条件）① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判别步骤：判别技巧：如何判别
充要条件练习1.给出下列四组命题:
(1)p:x=1; q: x2-4x+3=0.
(2)p:两个三角形相似; q:两个三角形全等.
(3)p: m<-2; q:方程x2-x-m=0无实根.
(4)p:一个四边形是矩形; q:四边形的对角线相等.
试分别指出p是q的什么条件.P是q的充分不必要条件P是q的必要不充分条件P是q的充分不必要条件P是q的充分不必要条件2．设Ｐ,Q是非空集合，命题甲为P∩Q=P∪Q；命题乙为：P?Q，那么甲是乙的（　　　　）
A.充分非必要条件　　　B.必要非充分条件
C.充分必要条件　　D.既非充分条件，也非必要条件3.在?ABC中“B=600”是“三内角A,B,C满足2B=A+C”的( )
A.充分非必要条件　　　B.必要非充分条件
C.充分必要条件　　D.既非充分条件，也非必要条件AC1.2 充要条件第2课时p是q的充分不必要条件。p是q的充要条件。p是q的必要不充分条件。p是q的既不充分也不必要条件。各种条件的可能情况① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判别步骤：判别技巧：复习引入 A练习：2.下列四个结论:
①“x=y”是“x2=y2”的充分不必要条件;
②“|x|=|y|”是“x2=y2”的必要不充分条件:
③两个三角形面积相等是它们全等的必要不充分条件;
④在平面上,“一个四边形的四边相等”是“这个四边形为菱形”的充要条件.
其中,正确的有____________.①③④3、若p:a为奇数,b是偶数, q: ab是偶数,则p是q的( )
A.充分非必要条件　　　B.必要非充分条件
C.充分必要条件　　D.既非充分条件，也非必要条件
A4、使不等式2x2-5x-3≥0成立的一个充分非必要条件是（ ）
A.x<0 B.x≥0 C.x∈{-1,3,5} Dx≤-1/2或x≥3C6.已知p、q都是r的必要条件,s是r的充分条件,q是s的充分条件,那么，
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)p是q的什么条件?5.a=3的一个必要不充分条件是_________;
a+b>0的一个充分不必要条件是____________.a>0a>0且b>0s是q的充要条件,r是q的充要条件,
p是q的必要不充分条件新课：
充要条件的证明注意：1.注意大前提,
2.分清p与q.①从命题角度看引申(一)若p则q是真命题, 那么p是q的充分条件 q是p的必要条件.(二)若p则q是真命题，若q则p为假命题, 那么p是q 的充分不必要条件，q是p必要不充分条件.（四）若p则q，若q则p都是假命题, 那么p是q的既不充分也不必要条件，q是p既不充分也不必要条件.(三）若p则q，若q则p都是真命题, 那么p是q的充要条件②从集合角度看
引申p是q的充分不必要条件。p是q的充要条件。p是q的必要不充分条件。p是q的既不充分也不必要条件。各种条件的可能情况① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判别步骤：判别技巧：课堂小结探讨下列生活中名言名句的充要关系。（1） 水滴石穿。（2） 骄兵必败。（3） 有志者事竟成。（4） 头发长，见识短。（5） 名师出高徒。（6） 放下屠刀，立地成佛。（7） 兔子尾巴长不了。（8） 不到长城非好汉。（9） 春回大地，万物复苏。（10）海内存知己。（11）蜡炬成灰泪始干。（12）玉不琢，不成器。常用正面叙述词及它的否定. ?等于不等于小于不小于大于不大于是不是都是不都是至多有
一个至少有
两个
至少有
一个一个也
没有至多有
n个至少有
n+1个任意的某个所有的某些常用正面叙述词及它的否定. ? D B例7、若p是r的充分不必要条件，r是q的必要
条件，r又是s的充要条件，q是s的必要条件.
则：
1）s是p的什么条件？
2）r是q的什么条件？必要不充分条件充要条件6.ax2+2x+1=0至少有一个负的实根的充要条件是( )
A. 0即“若┐q ┐p成立，则p是q的充分条件，q是p的必要条件” （1）直接利用定义判断：即“若p q成立，则p是q的充分条件，q是p的必要条件”.
（条件与结论是相对的）例1：指出下列各组命题中，p是q的什么条件， q是p的什么条件：
（1） p：x-1=0；q：(x-1)(x+2)=0.
（2） p：两条直线平行；q：内错角相等.
（3） p：a>b；q：a2>b2
（4） p：四边形的四条边相等；
q：四边形是正四边形. 二、新课复 习小 结作 业新 课