二次函数的应用（1）

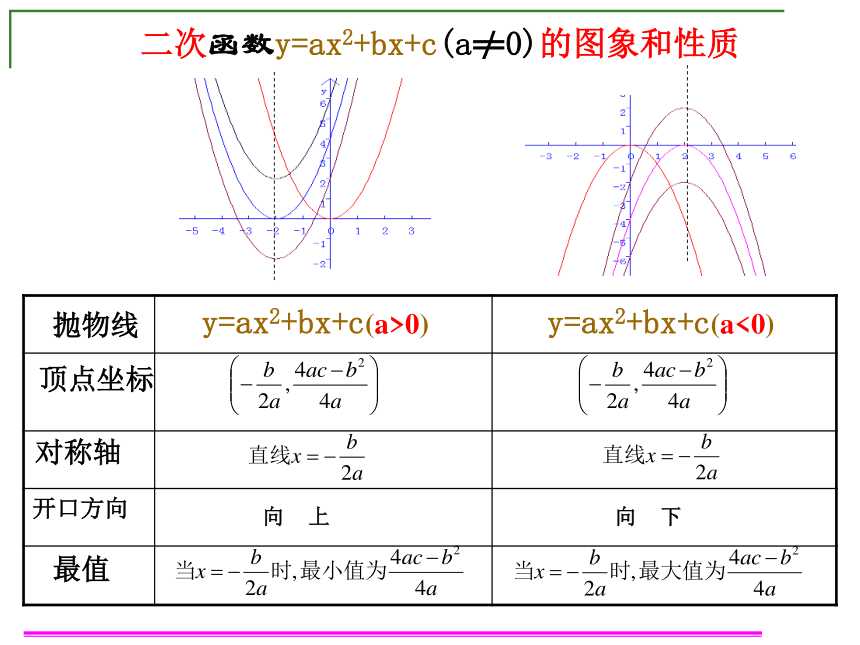
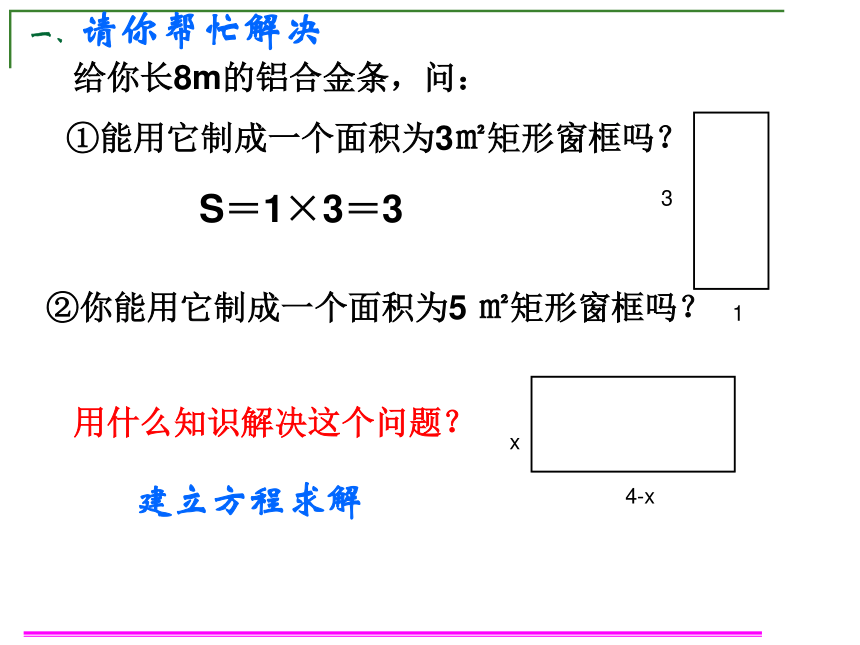
课件13张PPT。§6．4 二次函数的应用(1) 二次函数y=ax2+bx+c(a≠0)的图象和性质抛物线顶点坐标对称轴最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)向 上向 下一、请你帮忙解决给你长8m的铝合金条，问：①能用它制成一个面积为3㎡矩形窗框吗？S＝1×3＝3②你能用它制成一个面积为5 ㎡矩形窗框吗？ 用什么知识解决这个问题？建立方程求解一、请你帮忙解决给你长8m的铝合金条，问：③怎样设计，窗框的透光面积最大？为什么？ 在一些涉及到变量的最大值或最小值的应用问题中，可以考虑建立二次函数模型，利用二次函数最值方面的性质去解决。步骤：①设自变量； ②建立函数的解析式； ③确定自变量的取值范围；④根据顶点坐标公式或配方法求出最大值或最小值（在自变量的取值范围内）。用什么知识解决这个问题？例：某种粮大户去年种植优水稻360亩，今年计划多承租100～150亩稻田。预计原360亩稻田今年每亩可收益440元，新增稻田x今年每亩收益为（440-2x）元。试问：该种粮大户今年要承租多少亩稻田，才能使总收益最大？最大收益是多少？到新农村去 某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出30件，已知商品的进价为每件40元。 如何定价才能使利润最大？到商场去分析：
有涨价和降价两种情况;应分别考虑 某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出30件，已知商品的进价为每件40元，如何定价才能使利润最大？解： ⑴设每件涨价x元，每星期售出商品的利润为y元，则每星期少卖 件，实际卖出 件,每件获利为 元。　　　　　　　　　　　　　　　10x(300-10x)(20+x)y=(20+x)(300-10x)即(0≤X<30)所以：当x=5时，y有最大值6250 试一试（2）设降价x元，则每星期可多卖30x件，实际卖出（300+30x)件，每件获利为(20-x)元。答：定价为 55 元时，利润最大，最大利润为6750元 y=(20－x)(300＋30x) （0 ≤ X<20）综上所述，采用降价5元，即定价为55元时，可获最大利润。所以：当x=5时，y有最大值6750 分类研究是数学常用的思想方法练一练1、用长8m的铝合金条，设计成如图所示的矩形窗户框，窗户的宽和高各为多少时，该窗的透光面积最大（不计铝合金型材的宽度）？2.某商场以每件42元的价格购进一种服装，由试销知，每天的销量t（件）与的销售价x（元/件）之间的函数关系为t= -3x+240，每天的固定费用为200元. 问商场要想每天获得最大销售毛利润，每件的销售价应定为多少元？最大毛利润为多少？（每天的毛利润＝每天服装销售额－进货成本－固定费用）二次函数的应用二次函数是一类研究最优化问题的数学模型 1、分析和表示实际问题中变量之间的二次函数关系，建立二次函数模型 ；2、运用二次函数的知识求出最值；小 结3、根据实际意义、自变量的取值范围，给出实际问题的答案。思考题：某饮料经营部每天的固定成本为200元,某销售的饮料每瓶进价为5元,经调查得如下数据：
(1)设销售单价为x元时，日均销售量为y瓶，则y关于x的函数解析式是____________________
(3)设日均毛利润(毛利润＝销售额－进货成本－固定成本)为W元，求W关于x的函数解析式；
(3)若要使日均毛利润达到最大，销售单价应定为多少元(精确到0.1元)？最大日均毛利润为多少？来到商场再 见！