人教版2024—2025学年八年级下学期数学期中考试模拟试卷A卷(含解析)
文档属性
| 名称 | 人教版2024—2025学年八年级下学期数学期中考试模拟试卷A卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 739.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 06:25:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下学期数学期中考试模拟试卷A卷
满分:120分 时间:120分钟 范围:第十六章到第十八章
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各式中,属于最简二次根式的是( )
A. B. C. D.
2.如果二次根式有意义,那么x的取值范围是( )
A.x≥3 B.x≥0 C.x>3 D.x≠3
3.下列各组数据分别是线段a,b,c的长,能组成直角三角形的是( )
A.7,2,9 B.4,5,6 C.3,4,5 D.5,10,13
4.在平行四边形ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
5.下列计算正确的是( )
A. B.
C. D.
6.如图,在平行四边形ABCD中,AB=6,AD=10,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.2 B.4 C.6 D.8
7.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.AB=CD,AO=CO
C.AD∥BC,AD=BC D.∠BAD=∠BCD,AB∥CD
8.已知a、b、c在数轴上的位置如图所示,则|a+c+b|的化简结果是( )
A.b﹣2c B.b﹣2a C.﹣2a﹣b D.2c﹣b
9.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
10.如图,已知菱形ABCD的边长为12,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.已知直角三角形的两条直角边长分别为2和3,则第三边长为 .
12.若,则m﹣n的值为 .
13.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 .
14.已知,则代数式的值是 .
15.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A,B,C的面积分别是8cm2,10cm2,14cm2,则正方形D的面积是 cm2.
16.如图,在菱形ABCD中,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B=45°,BC,则GH的最小值为 .
人教版2024—2025学年八年级下学期数学期中考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
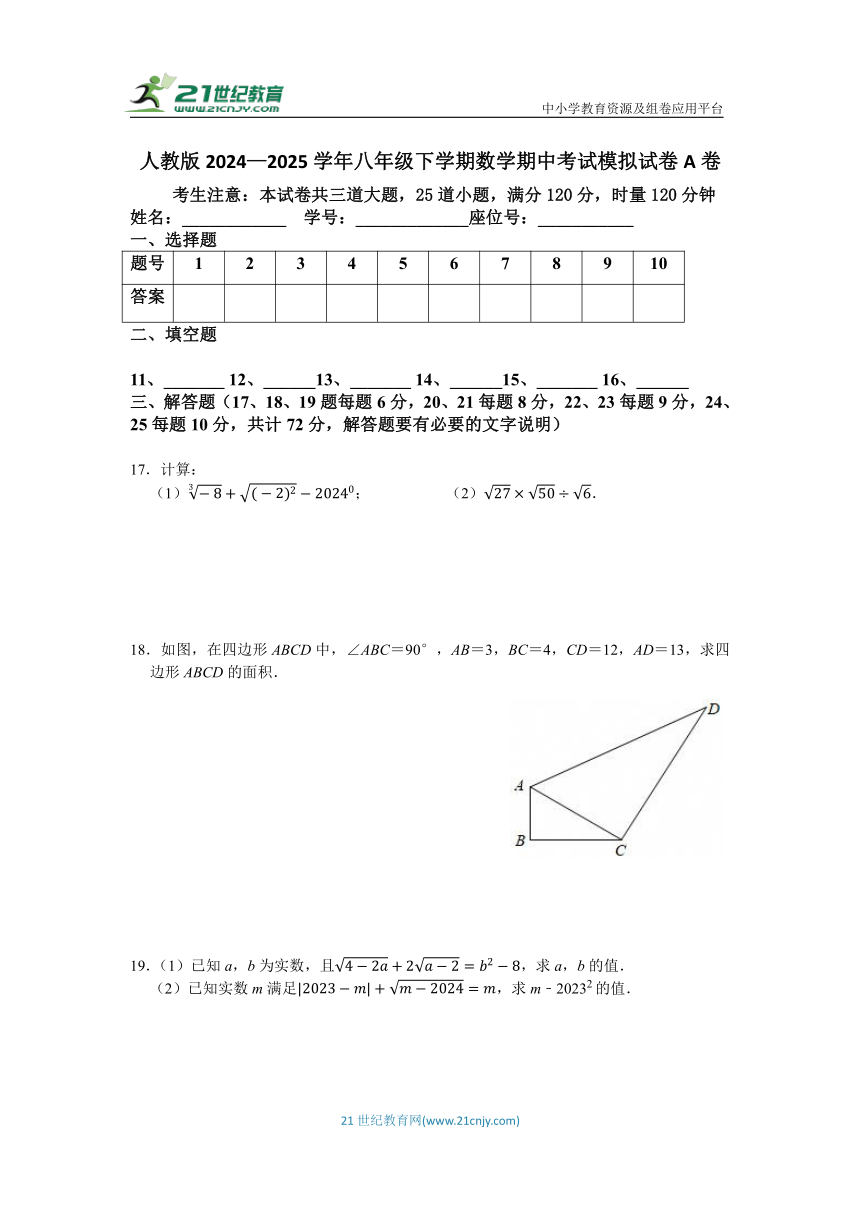
18.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
19.(1)已知a,b为实数,且,求a,b的值.
(2)已知实数m满足,求m﹣20232的值.
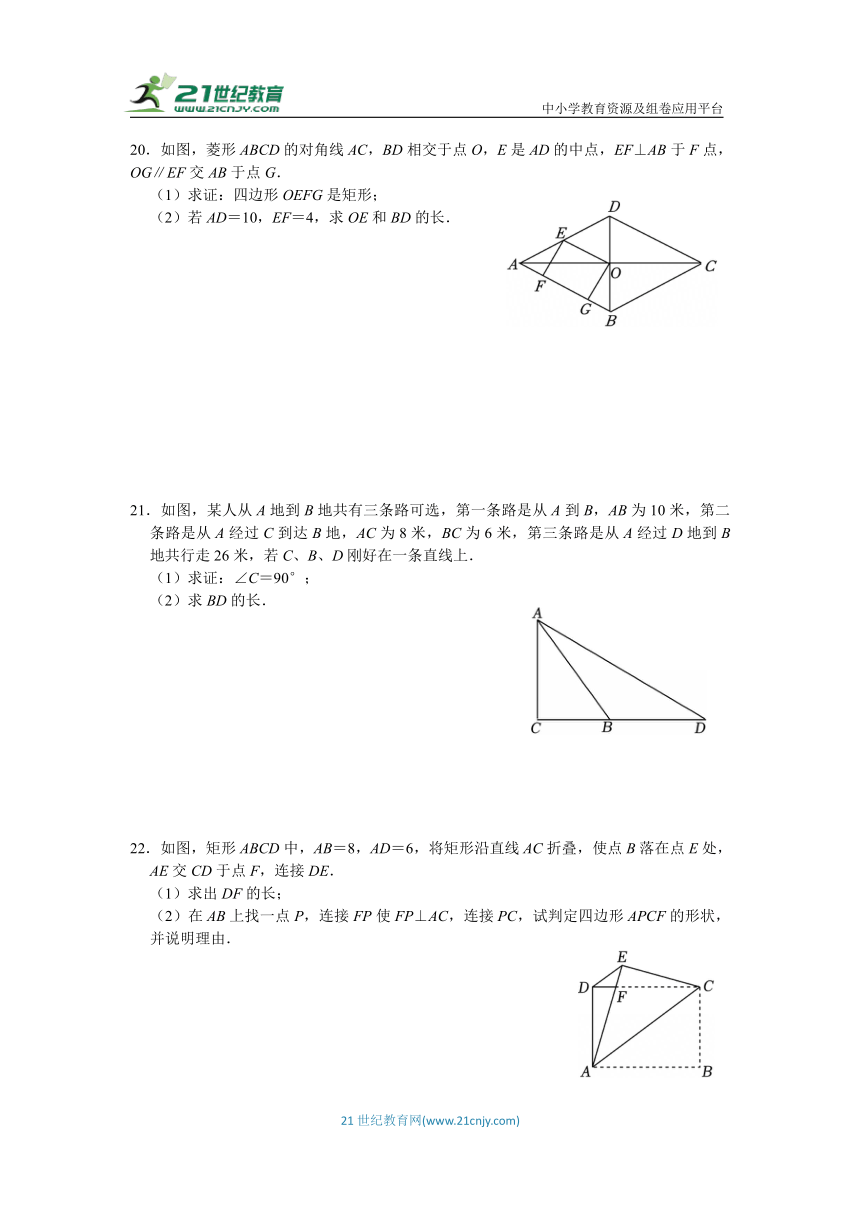
20.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,EF⊥AB于F点,OG∥EF交AB于点G.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BD的长.
21.如图,某人从A地到B地共有三条路可选,第一条路是从A到B,AB为10米,第二条路是从A经过C到达B地,AC为8米,BC为6米,第三条路是从A经过D地到B地共行走26米,若C、B、D刚好在一条直线上.
(1)求证:∠C=90°;
(2)求BD的长.
22.如图,矩形ABCD中,AB=8,AD=6,将矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求出DF的长;
(2)在AB上找一点P,连接FP使FP⊥AC,连接PC,试判定四边形APCF的形状,并说明理由.
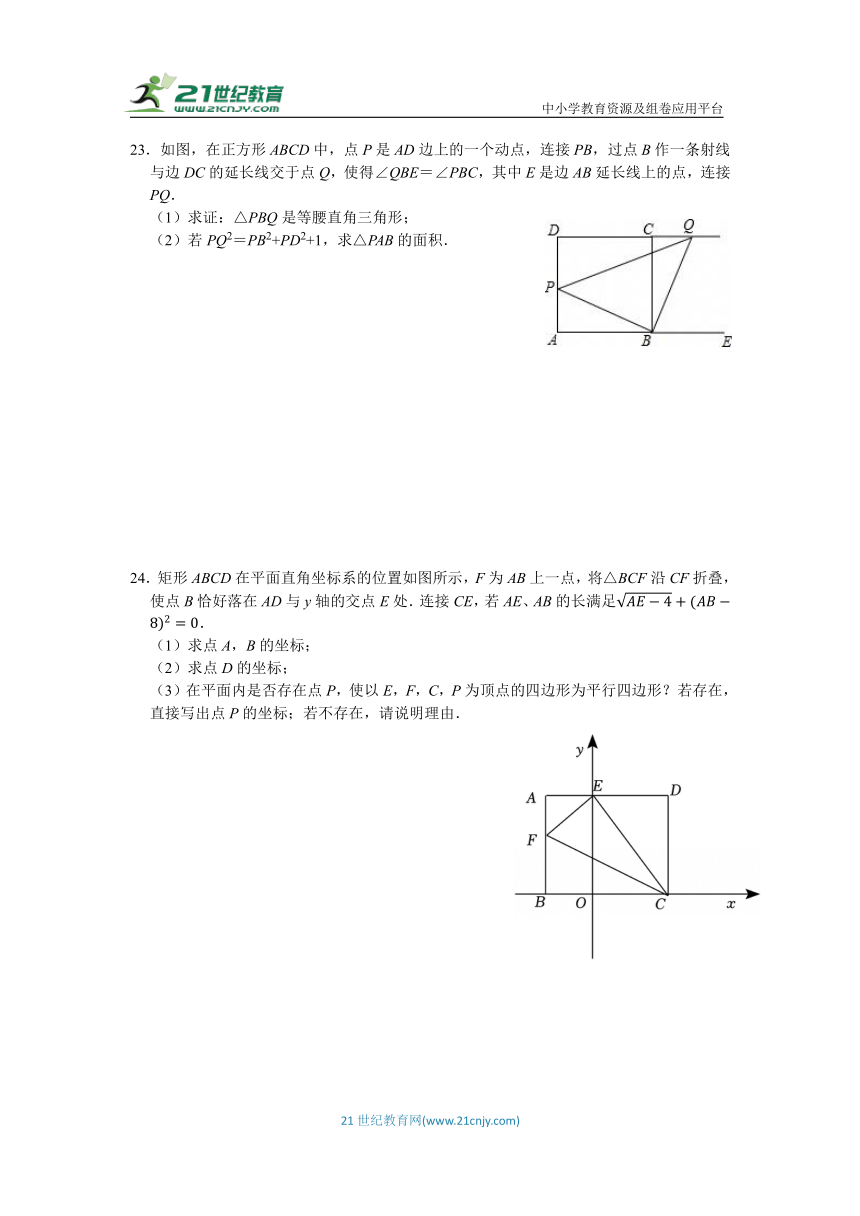
23.如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.
(1)求证:△PBQ是等腰直角三角形;
(2)若PQ2=PB2+PD2+1,求△PAB的面积.
24.矩形ABCD在平面直角坐标系的位置如图所示,F为AB上一点,将△BCF沿CF折叠,使点B恰好落在AD与y轴的交点E处.连接CE,若AE、AB的长满足.
(1)求点A,B的坐标;
(2)求点D的坐标;
(3)在平面内是否存在点P,使以E,F,C,P为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
25.如图,点A为y轴正半轴上一点,点B为x轴负半轴上一点,点C为x轴正半轴上一点,AO=a,BO=b,CO=c,且a,b,c满足.
(1)若c=3,求AB的值;
(2)已知点D为x轴上一动点,连接AD,以AD为边作等腰直角△ADE,∠DAE=90°.
①如图1,当点D在BC上运动时(点D不与B、C重合),连接CE,判断线段BD,CD,DE之间的数量关系,并说明理由;
②如图2,当点D在BC延长线上运动时,连接CE,BE,在(1)的条件下,若BE=10,求DE2的值;
(3)如图3,若点D在第一象限且在AC上方运动,连接AD,以AD为边作等腰直角△ADE,∠DAE=90°,连接BD,CE交于点F,连接CD,BE,在(1)的条件下,若CD=5,AD=6,求BE的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A C B D B B C C B
1.【解答】解:A、属于最简二次根式,故本选项符合题意;
B、不属于最简二次根式,故本选项不符合题意;
C、不属于最简二次根式,故本选项不符合题意;
D、不属于最简二次根式,故本选项不符合题意.
故选:A.
2.【解答】解:二次根式有意义,
则x的取值范围是:x≥3.
故选:A.
3.【解答】解:A.72+22=49+4=53≠92,所以7、2、9不能组成直角三角形;
B.42+52=16+25=41≠62,所以4、5、6不能组成直角三角形;
C.32+42=25=52,所以3、4、5可以组成直角三角形;
D.52+102=125≠132,所以5、10、13不能组成直角三角形;
故选:C.
4.【解答】解:在 ABCD中,∠A:∠B:∠C:∠D=2:3:2:3,
设每份比为x,则得到2x+3x+2x+3x=360°,
解得x=36°
则∠D=108°.
故选:B.
5.【解答】解:A. 2,所以A选项不符合题意;
B.236×2=12,所以B选项不符合题意;
C. (2)(2)=4﹣5=﹣1,所以C选项不符合题意;
D. 32,所以D选项符合题意;
故选:D.
6.【解答】解:如图,
∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=10,AB∥DC,
∴∠1=∠3,
又∵BF平分∠ABC,
∴∠1=∠2∠ABC,
∴∠2=∠3,
∴BC=CF,
∵BC=10,
∴CF=10,
∴DF=CF﹣DC=10﹣6=4.
所以DF的长为4,
故选:B.
7.【解答】解:A、根据对角线互相平分,可得四边形是平行四边形,可以证明四边形ABCD是平行四边形,故本选项错误;
B、AB=CD,AO=CO不能证明四边形ABCD是平行四边形,故本选项正确;
C、根据一组对边平行且相等的四边形是平行四边形可以证明四边形ABCD是平行四边形,故本选项错误;
D、根据AB∥CD可得:∠ABC+∠BCD=180°,∠BAD+∠ADC=180°,又由∠BAD=∠BCD可得:∠ABC=∠ADC,根据两组对角对应相等的四边形是平行四边形可以判定,故本选项错误;
故选:B.
8.【解答】解:由数轴可得:a+b+c<0,c﹣a<0,
|a+c+b|
=﹣(a+c+b)﹣(a﹣c)
=﹣a﹣c﹣b﹣a+c
=﹣2a﹣b.
故选:C.
9.【解答】解:连接AP,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=62+82=100,BC2=102=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∴当AP⊥BC时,AP有最小值,即EF有最小值,
∵△ABC的面积BC APAB AC,
∴BC AP=AB AC,
∴10AP=6×8,
∴AP,
∴AP=EF,
∴EF的最小值为,
故选:C.
10.【解答】解:∵菱形ABCD,∠ABC=120°,
∴∠DAB=60°,,AD=AB,
∵AD=AB,∠MAD=∠MAB,AM=AM,
∴△MAD≌△MAB(SAS),
∴DM=BM,
如图,作MH⊥AB于H,作DG⊥AB于G,
∴,
∴,
∴当D、M、H三点共线且DH⊥AB时,MA+MB+MD最小为2DG,
∴∠ADG=30°,
∴,
由勾股定理得,,
∴MA+MB+MD的最小值为,
故选:B.
二、填空题
11.【解答】解:∵直角三角形的两条直角边长分别为2和3,
∴第三边长为,
故答案为:.
12.【解答】解:根据题意得:,
解得:.
则m﹣n=3=(﹣1)=4.
故答案为:4.
13.【解答】解:∵AB=12,BC=5,
∴AD=5,BD13,
根据折叠可得:AD=A′D=5,
∴A′B=13﹣5=8,
设AE=x,则A′E=x,BE=12﹣x,
在Rt△A′EB中:(12﹣x)2=x2+82,
解得:x,
故答案为:.
14.【解答】解:
,
故答案为:.
15.【解答】解:根据勾股定理可知,
∵S正方形1+S正方形2=S大正方形=49cm2,
S正方形C+S正方形D=S正方形2,
S正方形A+S正方形B=S正方形1,
∴S大正方形=S正方形C+S正方形D+S正方形A+S正方形B=49cm2.
∴正方形D的面积=49﹣8﹣10﹣14=17(cm2);
故答案为:17.
16.【解答】解:连接AF,如图所示:
∵四边形ABCD是菱形,
∴AB=BC=2,
∵G,H分别为AE,EF的中点,
∴GH是△AEF的中位线,
∴GHAF,
当AF⊥BC时,AF最小,GH得到最小值,
则∠AFB=90°,
∵∠B=45°,
∴△ABF是等腰直角三角形,
∴AFAB2,
∴GH,
即GH的最小值为,
故答案为:.
三、解答题
17.【解答】解:(1)
=﹣2+2﹣1
=﹣1;
(2)
=15.
18.【解答】解:∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACDAB BCAC CD3×45×12=36.
故四边形ABCD的面积是36.
19.【解答】解:(1)∵和均有意义,
∴4﹣2a≥0且a﹣2≥0,
即a≤2且a≥2,
∴a=2,
当a=2时,,
可得b2﹣8=0,
∴b2=8,即,
∴a=2,;
(2)∵有意义,
∴m≥2024,
∴|2023﹣m|=m﹣2023,
因此,可变为,
即,
∴m﹣2024=20232,
即∴m﹣20232=2024,
∴m﹣20232的值是2024.
20.【解答】(1)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=10,AC⊥BD,
∴∠AOD=90°,
∵E是AD的中点,
∴,
由(1)可知,四边形EFCO是矩形,
∴FG=OE=5,
∵EF⊥AB,
∴∠EFA=90°,
∴,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2,
∵在直角三角形OGB中OB2=BG2+OG2=22+42=20,
∴,
∴.
21.【解答】(1)证明:∵AC=8米,BC=6米,AB=10米,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)解:设AD=x米,则BD=(26﹣x)米,
∴CD=BC+BD=6+26﹣x=(32﹣x)(米),
在Rt△ACD中,由勾股定理得:82+(32﹣x)2=x2,
解得:x=17,
则26﹣x=26﹣17=9,
答:BD的长为9米.
22.【解答】解:(1)∵矩形ABCD,
∴CD=AB=8,CD∥AB,∠ADC=90°,
∴∠DCA=∠BAC,
由折叠的性质可知,∠EAC=∠BAC,
∴∠EAC=∠DCA,
∴AF=CF,
设DF=x,则AF=CF=8﹣x,
由勾股定理得,AF2﹣DF2=AD2,即(8﹣x)2﹣x2=62,
解得,,
∴DF的长为;
(2)四边形APCF是菱形,理由如下;
如图,连接BD交AC于O,
∴O为AC的中点,
连接FO并延长,交AB于P,
∵AF=CF,OA=OC,
∴FP⊥AC,即点P即为所作;
∵∠FCO=∠PAO,OC=OA,∠FOC=∠POA,
∴△FCO≌△PAO(ASA),
∴OF=OP,
又∵OC=OA,FP⊥AC,
∴四边形APCF是菱形.
23.【解答】(1)证明:∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
,
∴△PAB≌△QCB(ASA),
∴PB=QB,
∴△PBQ是等腰直角三角形;
(2)解:设正方形的边长AB=a,PA=x,
∵△PAB≌△QCB,
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD﹣PA=a﹣x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a﹣x)2+(a+x)2=x2+a2+(a﹣x)2+1,
解得:2ax=1,
∴ax,
∵△PAB的面积SPA PBax.
24.【解答】解:(1)∵.
又∵0,(AB﹣8)2≥0,
∴AE=4,AB=8,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,AD∥BC,
∴AB⊥BC,
∴A(﹣4,8),B(﹣4,0);
(2)由翻折变换的性质可知CB=CE,
设CB=AD=CE=m,则DE=m﹣4,
∵∠D=90°,
∴CE2=DE2+CD2,
∴m2=(m﹣4)2+82,
∴m=10,
∴AD=BC=10,
∴DE=AD﹣AE=10﹣4=6,
∴D(6,8);
(3)由翻折变换的性质可知FE=FB,
设FE=FB=x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴EF2=AF2+AE2,
∴x2=(8﹣x)2+42,
∴x=5,
∴FE=FB=5,
∴F(﹣4,5),
∵E(0,8),C(6,0),
当EF是平行四边形的边时.P(2,﹣3),P′(10,3),
当EF是平行四边形的对角线时,P″(﹣10,13).
综上所述,满足条件的点P的坐标为(2,﹣3)或(10,3)或(﹣10,13).
25.【解答】解:(1)∵,
∴a﹣b≥0且b﹣a≥0,
∴a=b=c=3,
在Rt△AOB中,;
(2)①BD2+CD2=DE2;
理由如下:∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠ABD=45°,
∴∠DCE=∠ACE+∠ACD=45°+45°=90°,
∴在Rt△DCE中,CE2+CD2=DE2,
∴BD2+CD2=DE2;
②同①得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE=45°,BD=CE,
∴∠BCE=∠ACE+∠ACB=90°,
在Rt△BCE中,CE8,
∴BD=8,
∴CD=BD﹣BC=8﹣6=2,
∵∠BCE=90°,
∴∠DCE=90°,
在Rt△DCE中,DE2=CE2+CD2=82+22=68,
即DE2的值为68.
(3)∵AD=6,
∴在Rt△ADE中,DE2=AD2+AE2=62+62=72,
记EC与AD交于点G,同(2)得:△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,
又∠FGD=∠AGE,
∴∠DFE=∠EAD=90°,
在Rt△EFD和Rt△BFC中,DE2=EF2+DF2,BC2=BF2+CF2,
在Rt△EFB和Rt△DFC中,BE2=FE2+BF2,CD2=DF2+CF2,
∴DE2+BC2=BE2+CD2,
即72+36=BE2+25,
∴BE.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下学期数学期中考试模拟试卷A卷
满分:120分 时间:120分钟 范围:第十六章到第十八章
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列各式中,属于最简二次根式的是( )
A. B. C. D.
2.如果二次根式有意义,那么x的取值范围是( )
A.x≥3 B.x≥0 C.x>3 D.x≠3
3.下列各组数据分别是线段a,b,c的长,能组成直角三角形的是( )
A.7,2,9 B.4,5,6 C.3,4,5 D.5,10,13
4.在平行四边形ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
5.下列计算正确的是( )
A. B.
C. D.
6.如图,在平行四边形ABCD中,AB=6,AD=10,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.2 B.4 C.6 D.8
7.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.AB=CD,AO=CO
C.AD∥BC,AD=BC D.∠BAD=∠BCD,AB∥CD
8.已知a、b、c在数轴上的位置如图所示,则|a+c+b|的化简结果是( )
A.b﹣2c B.b﹣2a C.﹣2a﹣b D.2c﹣b
9.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
10.如图,已知菱形ABCD的边长为12,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.已知直角三角形的两条直角边长分别为2和3,则第三边长为 .
12.若,则m﹣n的值为 .
13.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 .
14.已知,则代数式的值是 .
15.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A,B,C的面积分别是8cm2,10cm2,14cm2,则正方形D的面积是 cm2.
16.如图,在菱形ABCD中,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B=45°,BC,则GH的最小值为 .
人教版2024—2025学年八年级下学期数学期中考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1); (2).
18.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
19.(1)已知a,b为实数,且,求a,b的值.
(2)已知实数m满足,求m﹣20232的值.
20.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,EF⊥AB于F点,OG∥EF交AB于点G.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BD的长.
21.如图,某人从A地到B地共有三条路可选,第一条路是从A到B,AB为10米,第二条路是从A经过C到达B地,AC为8米,BC为6米,第三条路是从A经过D地到B地共行走26米,若C、B、D刚好在一条直线上.
(1)求证:∠C=90°;
(2)求BD的长.
22.如图,矩形ABCD中,AB=8,AD=6,将矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求出DF的长;
(2)在AB上找一点P,连接FP使FP⊥AC,连接PC,试判定四边形APCF的形状,并说明理由.
23.如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.
(1)求证:△PBQ是等腰直角三角形;
(2)若PQ2=PB2+PD2+1,求△PAB的面积.
24.矩形ABCD在平面直角坐标系的位置如图所示,F为AB上一点,将△BCF沿CF折叠,使点B恰好落在AD与y轴的交点E处.连接CE,若AE、AB的长满足.
(1)求点A,B的坐标;
(2)求点D的坐标;
(3)在平面内是否存在点P,使以E,F,C,P为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
25.如图,点A为y轴正半轴上一点,点B为x轴负半轴上一点,点C为x轴正半轴上一点,AO=a,BO=b,CO=c,且a,b,c满足.
(1)若c=3,求AB的值;
(2)已知点D为x轴上一动点,连接AD,以AD为边作等腰直角△ADE,∠DAE=90°.
①如图1,当点D在BC上运动时(点D不与B、C重合),连接CE,判断线段BD,CD,DE之间的数量关系,并说明理由;
②如图2,当点D在BC延长线上运动时,连接CE,BE,在(1)的条件下,若BE=10,求DE2的值;
(3)如图3,若点D在第一象限且在AC上方运动,连接AD,以AD为边作等腰直角△ADE,∠DAE=90°,连接BD,CE交于点F,连接CD,BE,在(1)的条件下,若CD=5,AD=6,求BE的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A C B D B B C C B
1.【解答】解:A、属于最简二次根式,故本选项符合题意;
B、不属于最简二次根式,故本选项不符合题意;
C、不属于最简二次根式,故本选项不符合题意;
D、不属于最简二次根式,故本选项不符合题意.
故选:A.
2.【解答】解:二次根式有意义,
则x的取值范围是:x≥3.
故选:A.
3.【解答】解:A.72+22=49+4=53≠92,所以7、2、9不能组成直角三角形;
B.42+52=16+25=41≠62,所以4、5、6不能组成直角三角形;
C.32+42=25=52,所以3、4、5可以组成直角三角形;
D.52+102=125≠132,所以5、10、13不能组成直角三角形;
故选:C.
4.【解答】解:在 ABCD中,∠A:∠B:∠C:∠D=2:3:2:3,
设每份比为x,则得到2x+3x+2x+3x=360°,
解得x=36°
则∠D=108°.
故选:B.
5.【解答】解:A. 2,所以A选项不符合题意;
B.236×2=12,所以B选项不符合题意;
C. (2)(2)=4﹣5=﹣1,所以C选项不符合题意;
D. 32,所以D选项符合题意;
故选:D.
6.【解答】解:如图,
∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=10,AB∥DC,
∴∠1=∠3,
又∵BF平分∠ABC,
∴∠1=∠2∠ABC,
∴∠2=∠3,
∴BC=CF,
∵BC=10,
∴CF=10,
∴DF=CF﹣DC=10﹣6=4.
所以DF的长为4,
故选:B.
7.【解答】解:A、根据对角线互相平分,可得四边形是平行四边形,可以证明四边形ABCD是平行四边形,故本选项错误;
B、AB=CD,AO=CO不能证明四边形ABCD是平行四边形,故本选项正确;
C、根据一组对边平行且相等的四边形是平行四边形可以证明四边形ABCD是平行四边形,故本选项错误;
D、根据AB∥CD可得:∠ABC+∠BCD=180°,∠BAD+∠ADC=180°,又由∠BAD=∠BCD可得:∠ABC=∠ADC,根据两组对角对应相等的四边形是平行四边形可以判定,故本选项错误;
故选:B.
8.【解答】解:由数轴可得:a+b+c<0,c﹣a<0,
|a+c+b|
=﹣(a+c+b)﹣(a﹣c)
=﹣a﹣c﹣b﹣a+c
=﹣2a﹣b.
故选:C.
9.【解答】解:连接AP,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=62+82=100,BC2=102=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∴当AP⊥BC时,AP有最小值,即EF有最小值,
∵△ABC的面积BC APAB AC,
∴BC AP=AB AC,
∴10AP=6×8,
∴AP,
∴AP=EF,
∴EF的最小值为,
故选:C.
10.【解答】解:∵菱形ABCD,∠ABC=120°,
∴∠DAB=60°,,AD=AB,
∵AD=AB,∠MAD=∠MAB,AM=AM,
∴△MAD≌△MAB(SAS),
∴DM=BM,
如图,作MH⊥AB于H,作DG⊥AB于G,
∴,
∴,
∴当D、M、H三点共线且DH⊥AB时,MA+MB+MD最小为2DG,
∴∠ADG=30°,
∴,
由勾股定理得,,
∴MA+MB+MD的最小值为,
故选:B.
二、填空题
11.【解答】解:∵直角三角形的两条直角边长分别为2和3,
∴第三边长为,
故答案为:.
12.【解答】解:根据题意得:,
解得:.
则m﹣n=3=(﹣1)=4.
故答案为:4.
13.【解答】解:∵AB=12,BC=5,
∴AD=5,BD13,
根据折叠可得:AD=A′D=5,
∴A′B=13﹣5=8,
设AE=x,则A′E=x,BE=12﹣x,
在Rt△A′EB中:(12﹣x)2=x2+82,
解得:x,
故答案为:.
14.【解答】解:
,
故答案为:.
15.【解答】解:根据勾股定理可知,
∵S正方形1+S正方形2=S大正方形=49cm2,
S正方形C+S正方形D=S正方形2,
S正方形A+S正方形B=S正方形1,
∴S大正方形=S正方形C+S正方形D+S正方形A+S正方形B=49cm2.
∴正方形D的面积=49﹣8﹣10﹣14=17(cm2);
故答案为:17.
16.【解答】解:连接AF,如图所示:
∵四边形ABCD是菱形,
∴AB=BC=2,
∵G,H分别为AE,EF的中点,
∴GH是△AEF的中位线,
∴GHAF,
当AF⊥BC时,AF最小,GH得到最小值,
则∠AFB=90°,
∵∠B=45°,
∴△ABF是等腰直角三角形,
∴AFAB2,
∴GH,
即GH的最小值为,
故答案为:.
三、解答题
17.【解答】解:(1)
=﹣2+2﹣1
=﹣1;
(2)
=15.
18.【解答】解:∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACDAB BCAC CD3×45×12=36.
故四边形ABCD的面积是36.
19.【解答】解:(1)∵和均有意义,
∴4﹣2a≥0且a﹣2≥0,
即a≤2且a≥2,
∴a=2,
当a=2时,,
可得b2﹣8=0,
∴b2=8,即,
∴a=2,;
(2)∵有意义,
∴m≥2024,
∴|2023﹣m|=m﹣2023,
因此,可变为,
即,
∴m﹣2024=20232,
即∴m﹣20232=2024,
∴m﹣20232的值是2024.
20.【解答】(1)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=10,AC⊥BD,
∴∠AOD=90°,
∵E是AD的中点,
∴,
由(1)可知,四边形EFCO是矩形,
∴FG=OE=5,
∵EF⊥AB,
∴∠EFA=90°,
∴,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2,
∵在直角三角形OGB中OB2=BG2+OG2=22+42=20,
∴,
∴.
21.【解答】(1)证明:∵AC=8米,BC=6米,AB=10米,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)解:设AD=x米,则BD=(26﹣x)米,
∴CD=BC+BD=6+26﹣x=(32﹣x)(米),
在Rt△ACD中,由勾股定理得:82+(32﹣x)2=x2,
解得:x=17,
则26﹣x=26﹣17=9,
答:BD的长为9米.
22.【解答】解:(1)∵矩形ABCD,
∴CD=AB=8,CD∥AB,∠ADC=90°,
∴∠DCA=∠BAC,
由折叠的性质可知,∠EAC=∠BAC,
∴∠EAC=∠DCA,
∴AF=CF,
设DF=x,则AF=CF=8﹣x,
由勾股定理得,AF2﹣DF2=AD2,即(8﹣x)2﹣x2=62,
解得,,
∴DF的长为;
(2)四边形APCF是菱形,理由如下;
如图,连接BD交AC于O,
∴O为AC的中点,
连接FO并延长,交AB于P,
∵AF=CF,OA=OC,
∴FP⊥AC,即点P即为所作;
∵∠FCO=∠PAO,OC=OA,∠FOC=∠POA,
∴△FCO≌△PAO(ASA),
∴OF=OP,
又∵OC=OA,FP⊥AC,
∴四边形APCF是菱形.
23.【解答】(1)证明:∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
,
∴△PAB≌△QCB(ASA),
∴PB=QB,
∴△PBQ是等腰直角三角形;
(2)解:设正方形的边长AB=a,PA=x,
∵△PAB≌△QCB,
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD﹣PA=a﹣x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a﹣x)2+(a+x)2=x2+a2+(a﹣x)2+1,
解得:2ax=1,
∴ax,
∵△PAB的面积SPA PBax.
24.【解答】解:(1)∵.
又∵0,(AB﹣8)2≥0,
∴AE=4,AB=8,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,AD∥BC,
∴AB⊥BC,
∴A(﹣4,8),B(﹣4,0);
(2)由翻折变换的性质可知CB=CE,
设CB=AD=CE=m,则DE=m﹣4,
∵∠D=90°,
∴CE2=DE2+CD2,
∴m2=(m﹣4)2+82,
∴m=10,
∴AD=BC=10,
∴DE=AD﹣AE=10﹣4=6,
∴D(6,8);
(3)由翻折变换的性质可知FE=FB,
设FE=FB=x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴EF2=AF2+AE2,
∴x2=(8﹣x)2+42,
∴x=5,
∴FE=FB=5,
∴F(﹣4,5),
∵E(0,8),C(6,0),
当EF是平行四边形的边时.P(2,﹣3),P′(10,3),
当EF是平行四边形的对角线时,P″(﹣10,13).
综上所述,满足条件的点P的坐标为(2,﹣3)或(10,3)或(﹣10,13).
25.【解答】解:(1)∵,
∴a﹣b≥0且b﹣a≥0,
∴a=b=c=3,
在Rt△AOB中,;
(2)①BD2+CD2=DE2;
理由如下:∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ACE=∠ABD=45°,
∴∠DCE=∠ACE+∠ACD=45°+45°=90°,
∴在Rt△DCE中,CE2+CD2=DE2,
∴BD2+CD2=DE2;
②同①得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE=45°,BD=CE,
∴∠BCE=∠ACE+∠ACB=90°,
在Rt△BCE中,CE8,
∴BD=8,
∴CD=BD﹣BC=8﹣6=2,
∵∠BCE=90°,
∴∠DCE=90°,
在Rt△DCE中,DE2=CE2+CD2=82+22=68,
即DE2的值为68.
(3)∵AD=6,
∴在Rt△ADE中,DE2=AD2+AE2=62+62=72,
记EC与AD交于点G,同(2)得:△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,
又∠FGD=∠AGE,
∴∠DFE=∠EAD=90°,
在Rt△EFD和Rt△BFC中,DE2=EF2+DF2,BC2=BF2+CF2,
在Rt△EFB和Rt△DFC中,BE2=FE2+BF2,CD2=DF2+CF2,
∴DE2+BC2=BE2+CD2,
即72+36=BE2+25,
∴BE.
21世纪教育网(www.21cnjy.com)
同课章节目录
