19.1.2 函数的图像课件
图片预览



文档简介
课件21张PPT。19.1 函数第1课时 函数的图象19.1.2 函数的函数情景
导入合作
探究课堂
小结随堂
训练学习目标2.会用描点法画出函数图象,能说出画函数图象的步骤;1.会看函数图象,能用文字语言描述函数图象所反
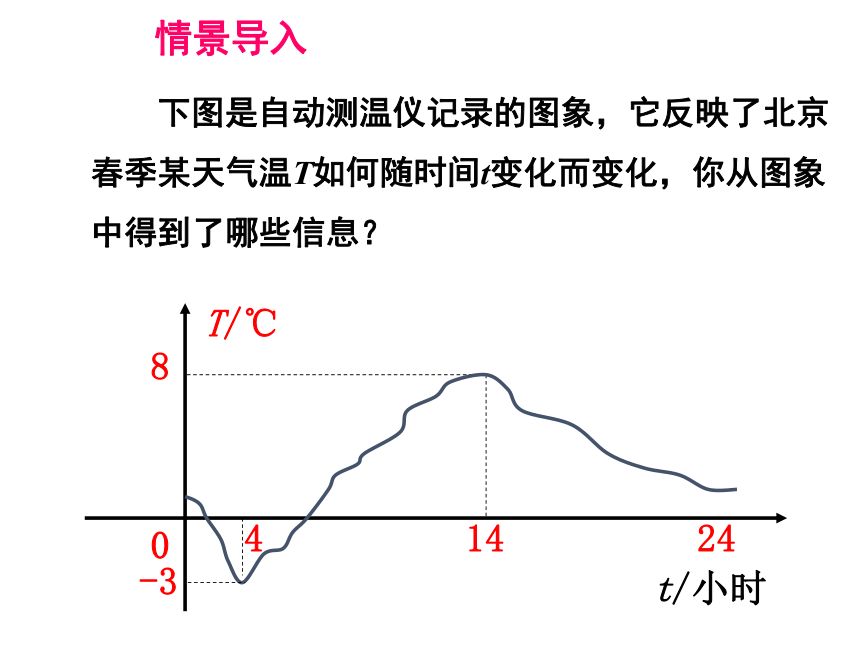
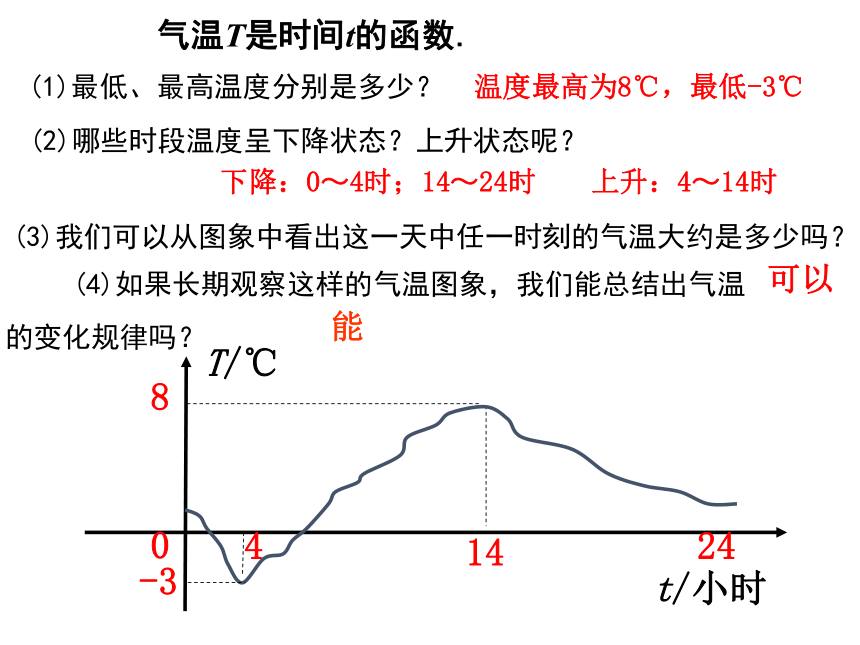
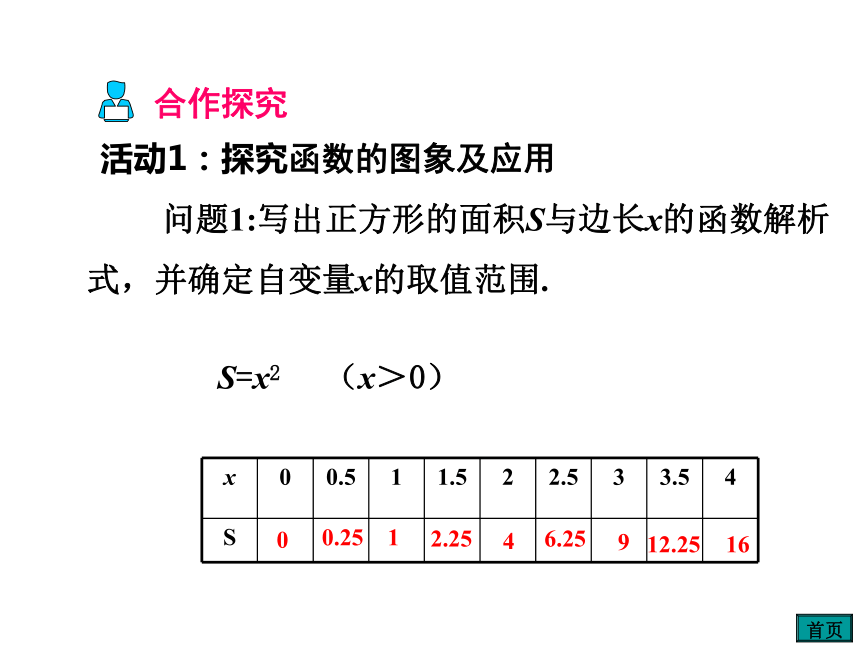
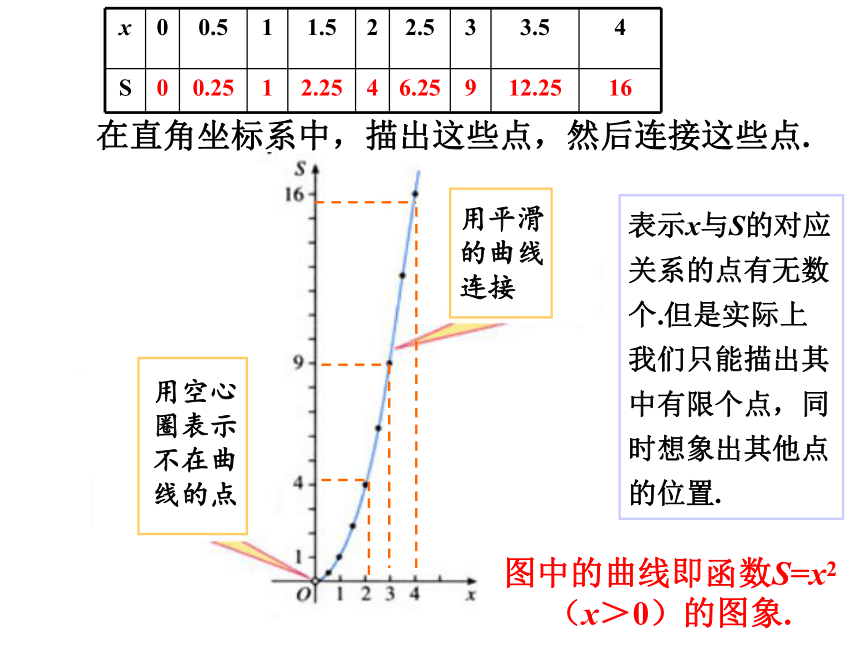
映的情形;3.会判断一个点是否在函数图象上. 下图是自动测温仪记录的图象,它反映了北京春季某天气温T如何随时间t变化而变化,你从图象中得到了哪些信息?414248T/℃0-3t/小时情景导入414248T/℃0-3t/小时气温T是时间t的函数.(1)最低、最高温度分别是多少?温度最高为8℃,最低-3℃ (2)哪些时段温度呈下降状态?上升状态呢?下降:0~4时;14~24时上升:4~14时(3)我们可以从图象中看出这一天中任一时刻的气温大约是多少吗?可以 (4)如果长期观察这样的气温图象,我们能总结出气温的变化规律吗?能 问题1:写出正方形的面积S与边长x的函数解析式,并确定自变量x的取值范围.S=x2(x>0)00.2512.2546.25912.2516合作探究活动1:探究函数的图象及应用在直角坐标系中,描出这些点,然后连接这些点.表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.用空心
圈表示
不在曲
线的点用平滑
的曲线
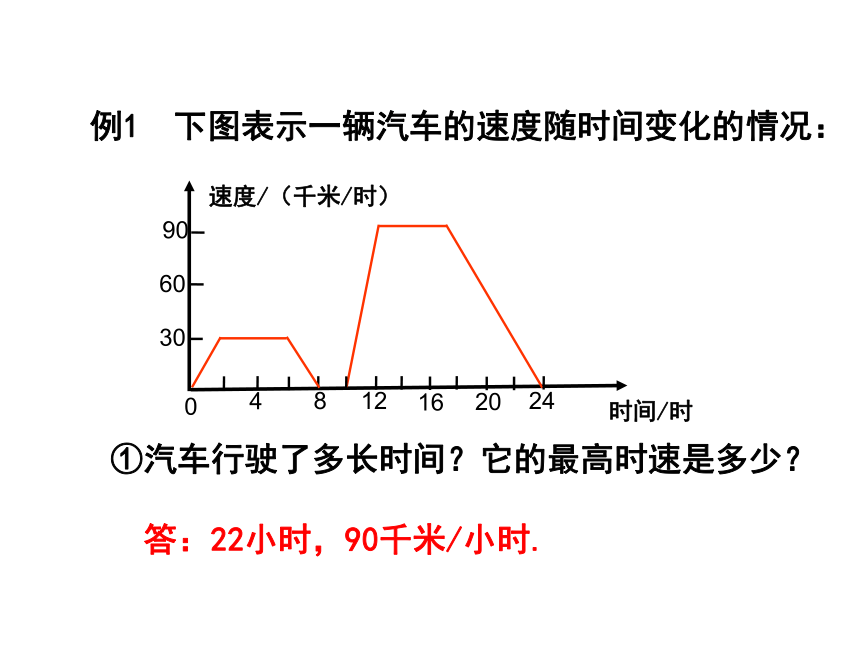
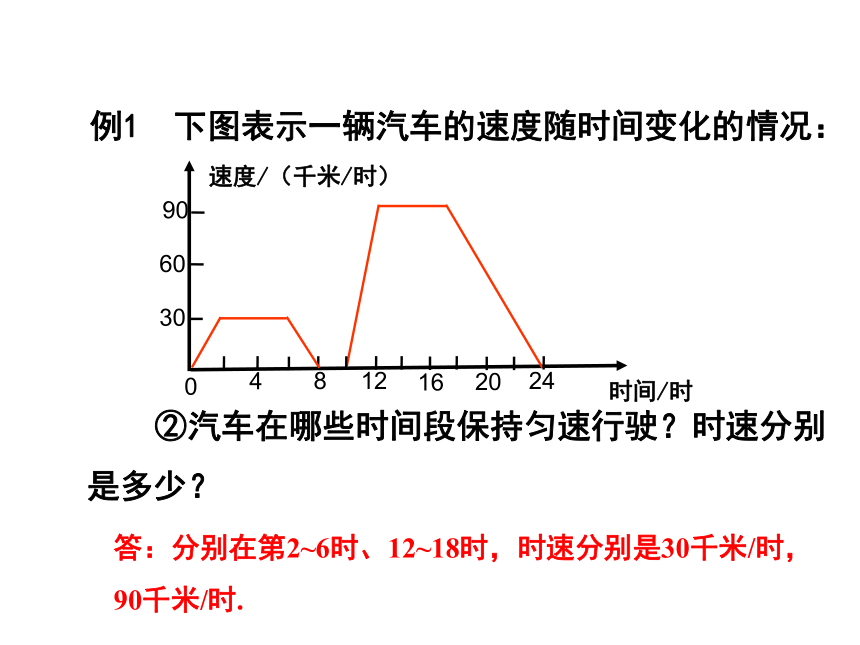
连接图中的曲线即函数S=x2 (x>0)的图象. 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象. 函数图象是典型的数形结合,图象应用广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.知识要点例1 下图表示一辆汽车的速度随时间变化的情况: ①汽车行驶了多长时间?它的最高时速是多少?
答:22小时,90千米/小时. ②汽车在哪些时间段保持匀速行驶?时速分别是多少? 答:分别在第2~6时、12~18时,时速分别是30千米/时,90千米/时.例1 下图表示一辆汽车的速度随时间变化的情况: ③出发后8时到10时之间可能发生了什么情况?答:可能发生了停车休息.例1 下图表示一辆汽车的速度随时间变化的情况: 速度/(千米/时)例1 下图表示一辆汽车的速度随时间变化的情况: ④用自己的语言大致描述这辆汽车的行驶情况. 答:这辆车从出发地开始启动至第2分钟处匀加速行驶,第2分钟至第6分钟保持30千米/时的速度行驶,第6分钟至第8分钟处于匀减速行驶,中途停车休息了2分钟,第10分钟到第12分钟处于匀加速到90千米/时,第12分钟至第18分钟保持90千米/时的速度行驶,第18分钟至第24分钟处于匀减速行驶行驶,到达了目的地.方法小结:
函数图象直观的反映两变量之间的关系.同学们在说图
象时可从以下“五个要素”去说:
①两变量之间的实际意义什么,各用哪一个轴表示;
②每个轴用的单位是什么;
③原点的实际意义是什么;
④图象上各点的意义,标出的端点,并说出他们的意义;
⑤图象上各个分段的解析式. 问题: 函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.那么,怎样画一个函数的图象呢? 活动2:探究画函数图象的方法 -6 6-3-2-1.2-1.5 3 21.51.2为什么没有“0”? 试画出函数 的图象.解:(1)列表 取自变量的一些值,并求出对应的函数值,填入表中.解:(1)列表(2)描点 分别以表中
对应的x、y为横纵
坐标,在坐标系中描
出对应的点.(3)连线 用光滑的曲
线把这些点依次连
接起来. -6 6-3-2-1.2-1.5 3 21.51.2(1,-6)(1)列表(表中给出一些自变量的值及其对应的函数)(2)描点:(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点)(3)连线:(按照横坐标由小到大的顺序把所描的各点用平滑的曲线连接起来)1.画函数的图象的一般步骤:注意:列表时自变量由小到大,相差一样,有时需对称.知识要点(1)函数图象上点的横坐标和纵坐标分别表示什么?
(2)画函数图象时,能画出满足函数关系的所有的点吗?
(3)你认为观察函数图象时要注意哪些问题?
(4)函数图像画法.图象信息(形) 图象上点的坐标特点(数) 对应关系和变化规律 2.画函数的图象应弄清的问题:例2.作出y=2x+1的图象?解:列表-3-1153连线:描点:y=2x+1函数y=2x+1的图象是一条直线.解:列表-3-1153我们知道,函数图象是以自变量的值和对应的函数值分别为横、纵坐标的点组成的图形,这样的点有无数个,那么怎样判断一个点是否在函数图象上? 判断下列各点是否在函数 的图象上?
①(-4,-7); ②(4,4.5).判断方法:通常的方法是把点的横坐标(即自变量x)的取值代入解析式求出相应的函数值y值,看是否等于该点的纵坐标,如果等于,则该点在函数图象上;如不在,则该点不在函数图象上.这节课我们学习了什么内容?了解了函数图象的概念;会用描点法画函数的图象;会判断一个点是否在函数图象上.课堂小结
导入合作
探究课堂
小结随堂
训练学习目标2.会用描点法画出函数图象,能说出画函数图象的步骤;1.会看函数图象,能用文字语言描述函数图象所反
映的情形;3.会判断一个点是否在函数图象上. 下图是自动测温仪记录的图象,它反映了北京春季某天气温T如何随时间t变化而变化,你从图象中得到了哪些信息?414248T/℃0-3t/小时情景导入414248T/℃0-3t/小时气温T是时间t的函数.(1)最低、最高温度分别是多少?温度最高为8℃,最低-3℃ (2)哪些时段温度呈下降状态?上升状态呢?下降:0~4时;14~24时上升:4~14时(3)我们可以从图象中看出这一天中任一时刻的气温大约是多少吗?可以 (4)如果长期观察这样的气温图象,我们能总结出气温的变化规律吗?能 问题1:写出正方形的面积S与边长x的函数解析式,并确定自变量x的取值范围.S=x2(x>0)00.2512.2546.25912.2516合作探究活动1:探究函数的图象及应用在直角坐标系中,描出这些点,然后连接这些点.表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.用空心
圈表示
不在曲
线的点用平滑
的曲线
连接图中的曲线即函数S=x2 (x>0)的图象. 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象. 函数图象是典型的数形结合,图象应用广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.知识要点例1 下图表示一辆汽车的速度随时间变化的情况: ①汽车行驶了多长时间?它的最高时速是多少?
答:22小时,90千米/小时. ②汽车在哪些时间段保持匀速行驶?时速分别是多少? 答:分别在第2~6时、12~18时,时速分别是30千米/时,90千米/时.例1 下图表示一辆汽车的速度随时间变化的情况: ③出发后8时到10时之间可能发生了什么情况?答:可能发生了停车休息.例1 下图表示一辆汽车的速度随时间变化的情况: 速度/(千米/时)例1 下图表示一辆汽车的速度随时间变化的情况: ④用自己的语言大致描述这辆汽车的行驶情况. 答:这辆车从出发地开始启动至第2分钟处匀加速行驶,第2分钟至第6分钟保持30千米/时的速度行驶,第6分钟至第8分钟处于匀减速行驶,中途停车休息了2分钟,第10分钟到第12分钟处于匀加速到90千米/时,第12分钟至第18分钟保持90千米/时的速度行驶,第18分钟至第24分钟处于匀减速行驶行驶,到达了目的地.方法小结:
函数图象直观的反映两变量之间的关系.同学们在说图
象时可从以下“五个要素”去说:
①两变量之间的实际意义什么,各用哪一个轴表示;
②每个轴用的单位是什么;
③原点的实际意义是什么;
④图象上各点的意义,标出的端点,并说出他们的意义;
⑤图象上各个分段的解析式. 问题: 函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.那么,怎样画一个函数的图象呢? 活动2:探究画函数图象的方法 -6 6-3-2-1.2-1.5 3 21.51.2为什么没有“0”? 试画出函数 的图象.解:(1)列表 取自变量的一些值,并求出对应的函数值,填入表中.解:(1)列表(2)描点 分别以表中
对应的x、y为横纵
坐标,在坐标系中描
出对应的点.(3)连线 用光滑的曲
线把这些点依次连
接起来. -6 6-3-2-1.2-1.5 3 21.51.2(1,-6)(1)列表(表中给出一些自变量的值及其对应的函数)(2)描点:(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点)(3)连线:(按照横坐标由小到大的顺序把所描的各点用平滑的曲线连接起来)1.画函数的图象的一般步骤:注意:列表时自变量由小到大,相差一样,有时需对称.知识要点(1)函数图象上点的横坐标和纵坐标分别表示什么?
(2)画函数图象时,能画出满足函数关系的所有的点吗?
(3)你认为观察函数图象时要注意哪些问题?
(4)函数图像画法.图象信息(形) 图象上点的坐标特点(数) 对应关系和变化规律 2.画函数的图象应弄清的问题:例2.作出y=2x+1的图象?解:列表-3-1153连线:描点:y=2x+1函数y=2x+1的图象是一条直线.解:列表-3-1153我们知道,函数图象是以自变量的值和对应的函数值分别为横、纵坐标的点组成的图形,这样的点有无数个,那么怎样判断一个点是否在函数图象上? 判断下列各点是否在函数 的图象上?
①(-4,-7); ②(4,4.5).判断方法:通常的方法是把点的横坐标(即自变量x)的取值代入解析式求出相应的函数值y值,看是否等于该点的纵坐标,如果等于,则该点在函数图象上;如不在,则该点不在函数图象上.这节课我们学习了什么内容?了解了函数图象的概念;会用描点法画函数的图象;会判断一个点是否在函数图象上.课堂小结
