第 17章 函数及其图象 评估检测题(B卷) 单元测试 (无答案)2024-2025学年八年级下册数学华师版
文档属性
| 名称 | 第 17章 函数及其图象 评估检测题(B卷) 单元测试 (无答案)2024-2025学年八年级下册数学华师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 88.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 20:40:37 | ||
图片预览


文档简介
第 17章评估检测题(B卷)
(时间 :90分钟 总分 :100分)
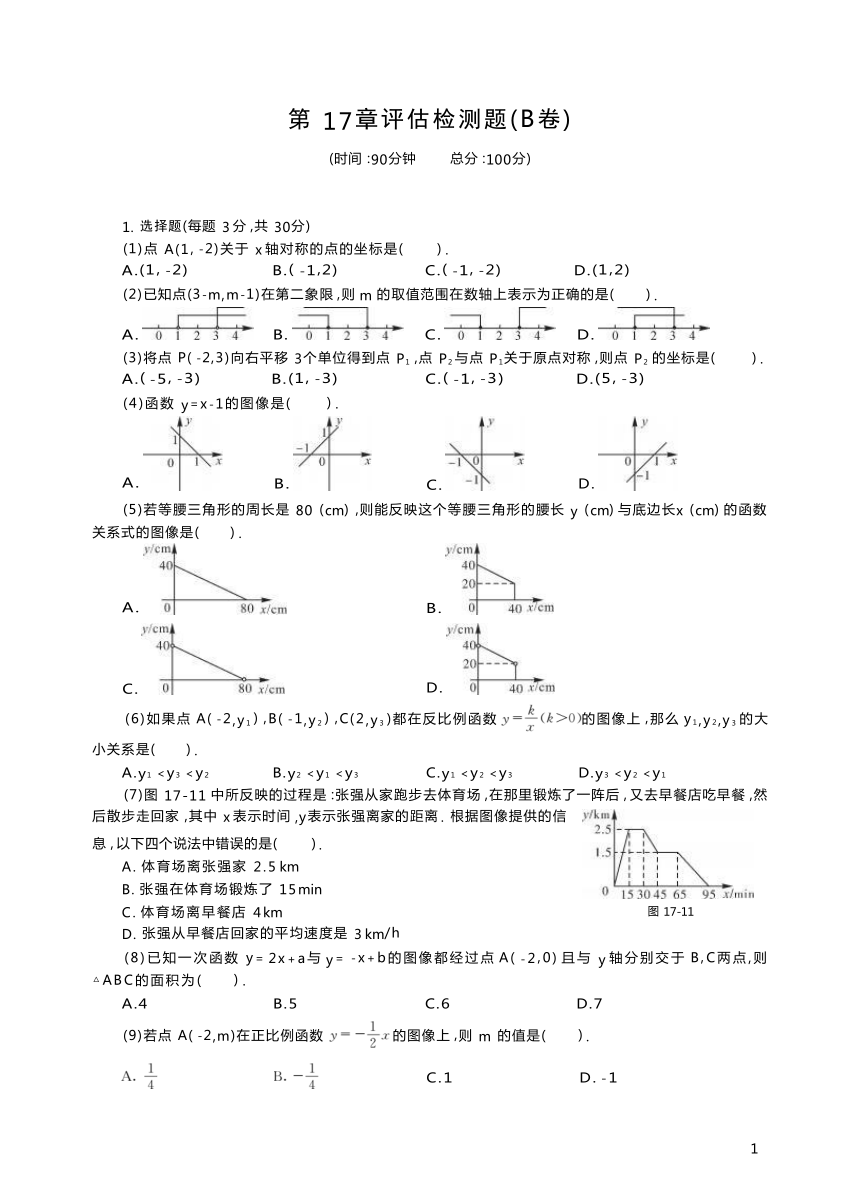
1. 选择题(每题 3 分 ,共 30分)
(1)点 A(1, -2)关于 x 轴对称的点的坐标是( ) .
A.(1, -2) B.( -1,2) C.( -1, -2) D.(1,2)
(2)已知点(3-m,m-1)在第二象限 ,则 m 的取值范围在数轴上表示为正确的是( ) .
A. B. C. D.
(3)将点 P( -2,3)向右平移 3个单位得到点 P1 ,点 P2 与点 P1关于原点对称 ,则点 P2 的坐标是( ) .
A.( -5, -3) B.(1, -3) C.( -1, -3) D.(5, -3)
(4)函数 y=x-1的图像是( ) .
1
A.
B.
C.
D.
(5)若等腰三角形的周长是 80 (cm) ,则能反映这个等腰三角形的腰长 y (cm) 与底边长x (cm) 的函数 关系式的图像是( ) .
A.
B.
C.
D.
(6)如果点 A( -2,y1 ) ,B( -1,y2 ) ,C(2,y3 )都在反比例函数 的图像上 ,那么 y1,y2,y3 的大
小关系是( ) .
A.y1(7)图 17-11 中所反映的过程是 :张强从家跑步去体育场 ,在那里锻炼了一阵后 , 又去早餐店吃早餐 ,然
后散步走回家 ,其中 x 表示时间 ,y表示张强离家的距离 . 根据图像提供的信
息 , 以下四个说法中错误的是( ) . A. 体育场离张强家 2.5 km
B. 张强在体育场锻炼了 15min C. 体育场离早餐店 4km
D. 张强从早餐店回家的平均速度是 3 km/h
图 17-11
(8)已知一次函数 y= 2x+a与 y= -x+b的图像都经过点 A( -2,0) 且与 y 轴分别交于 B,C两点,则
△ABC的面积为( ) .
A.4 B.5 C.6 D.7
(9)若点 A( -2,m)在正比例函数 的图像上 ,则 m 的值是( ) .
C.1 D. -1
(10)已知反比例函数的图像 有两点 A(x1,y1 ) 、B(x2,y2 ) ,若 y1 >y2 ,则 x1 -x2 的值是( ) .
A. 正数 B. 负数 C. 非正数 D. 不能确定
2. 填空题(每题 3 分 ,共 24分)
(1)已知反比例函数 则 自变量 x 的取值范围是 .
(2)若点 M(3,a)关于 y轴的对称点是点 N(b,2) ,则(a+b) 2 024 = .
(3)如图 17-12所示 ,直线 y= 2x+4与 x,y轴分别交于点 A,B两点 , 以 OB为边在 y 轴右侧作等边三 角形 OBC,将点 C向左平移 ,使其对应点 C'恰好落在直线 AB上 ,则点 C'的坐标为 .
(4)小明从家跑步到学校 ,接着马上原路步行回家 . 如图 17-13是小明离家的路程 y(m) 与时间 t(min) 的函数图像 ,则小明回家的速度是每分钟步行 m.
(5)直线 y=3x+2沿 y轴向下平移 5个单位 ,则平移后直线与 y轴的交点坐标为 .
(6)将一次函数 y= 3x- 1 的图像沿 y 轴向上平移 3 个单位后 ,得到的图像 对 应 的 函 数 关 系 式 为
.
(7)如图 17-14所示 , 已知直线 l1 :y=k1x+4与直线 l2 :y=k2x-5交于点 A,它们与 y轴的交点分别为 点 B,C,点 E,F分别为线段 AB,AC的中点,则线段 EF的长度为 .
图 17-12 图 17-13 图 17-14
(8)在反比例函数 的图像的每一条曲线上 ,y都随 x 的增大而减小 ,则 m 的取值范围是
.
3. 解答题(共 46分)
(1)已知某厂现有 A种金属 70t,B种金属 52t,现计划用这两种金属生产 M,N 两种型号的合金产品共 80000套 . 已知做一套 M 型号的合金产品需要 A 种金属 0.6 kg,B种金属 0.9 kg,可获利润 45元 ;做一套 N 种型号的合金产品需要 A种金属 1.1 kg,B种金属 0.4 kg,可获利润 50元 . 若设生产 N 种型号的合金产品 套数为 x,用这批金属生产这两种型号的合金产品所获总利润为 y元 . (6分)
①求 y与 x 的函数关系式 ,并求出 自变量 x 的取值范围 ;
②在生产这批合金产品时 ,N 型号的合金产品应生产多少套 ,该厂所获利润最大 最大利润是多少
2
(2)甲 、乙两支清雪队同时开始清理某路段积雪 ,一段时间后 , 乙队被调往别处 , 甲队又用了 3 h 完成了 剩余的清雪任务 , 已知甲队每小时的清雪量保持不变 , 乙队每小时清雪 50t, 甲 、乙两队在此路段的清雪总量 y(t)与清雪时间 x(时)之间的函数图像如图 17-15所示 . (8分)
①乙队调离时 , 甲 、乙两队已完成的清雪总量为 t.
②求此次任务的清雪总量 m.
③求乙队调离后 y与 x 之间的函数关系式 .
图 17-15
(3)如图 17-16(a)所示 ,长为 60 km 的某线路 AB上有甲 、乙两车 ,分别从南站 A 和北站 B 同时出发相 向而行 ,到达 B,A后立刻返回到出发站停止 ,速度均为 30 km/h. 设甲车 、乙车距南站 A 的路程分别为 y甲 , y乙 (km) ,行驶时间为 t(h) . (8分)
①图 17-16(b)已画出 y甲 与 t的函数图像 ,其中 a= ,b= ,c= ;
②分别写出 0≤t≤2及 2③在图 17-16(b)中补画 y乙 与 t的函数图像 ,并观察图像得出在整个行驶过程内两车相遇的次数 .
(a) (b)
图 17-16
3
(4)从甲地到乙地 ,先是一段平路 ,然后是一段上坡路 ,小明骑车从甲地出发 ,到达乙地后立即原路返回 甲地 . 途中休息了一段时间 . 假设小明骑车在平路 、上坡 、下坡时分别保持匀速前进 . 已知小明骑车上坡的速 度比在平路上的速度每小时少 5 km ,下坡的速度比在平路上的速度每小时多 5 km ,设小明出发 x h 后 , 到 达离甲地 y km 的地方 , 图 17-17中的折线 OABCDE 表示 y 与 x 之间的函数关系 . (8分)
①小明骑车在平路上的速度为 km/h;他途中休息了 h.
②求线段 AB,BC所表示的 y 与 x 之间的函数关系式 .
③如果小明两次经过途中某一地点的时间间隔为 0.15 h,那么该地点离甲地多远
图 17-17
(5)已知 A(x1 ,y1 ) ,B (x2,y2 )是反比例函数 图像上的两点,且 x1 - x2 = -2,x1 ·x2 = 3,y1 - y2 . 当 -3(6)如图 17-18所示 ,在平面直 角 坐 标 系 xOy中 , 直 线 y=mx 与 双 曲 线 相 交 于A( -1,a) ,B 两
点,BC垂直于 x 轴 ,垂足为 C,△AOC的面积是 1. (8分)
①求 m,n的值 ;
②求直线 AC的函数表达式 .
图 17-18
4
(时间 :90分钟 总分 :100分)
1. 选择题(每题 3 分 ,共 30分)
(1)点 A(1, -2)关于 x 轴对称的点的坐标是( ) .
A.(1, -2) B.( -1,2) C.( -1, -2) D.(1,2)
(2)已知点(3-m,m-1)在第二象限 ,则 m 的取值范围在数轴上表示为正确的是( ) .
A. B. C. D.
(3)将点 P( -2,3)向右平移 3个单位得到点 P1 ,点 P2 与点 P1关于原点对称 ,则点 P2 的坐标是( ) .
A.( -5, -3) B.(1, -3) C.( -1, -3) D.(5, -3)
(4)函数 y=x-1的图像是( ) .
1
A.
B.
C.
D.
(5)若等腰三角形的周长是 80 (cm) ,则能反映这个等腰三角形的腰长 y (cm) 与底边长x (cm) 的函数 关系式的图像是( ) .
A.
B.
C.
D.
(6)如果点 A( -2,y1 ) ,B( -1,y2 ) ,C(2,y3 )都在反比例函数 的图像上 ,那么 y1,y2,y3 的大
小关系是( ) .
A.y1
后散步走回家 ,其中 x 表示时间 ,y表示张强离家的距离 . 根据图像提供的信
息 , 以下四个说法中错误的是( ) . A. 体育场离张强家 2.5 km
B. 张强在体育场锻炼了 15min C. 体育场离早餐店 4km
D. 张强从早餐店回家的平均速度是 3 km/h
图 17-11
(8)已知一次函数 y= 2x+a与 y= -x+b的图像都经过点 A( -2,0) 且与 y 轴分别交于 B,C两点,则
△ABC的面积为( ) .
A.4 B.5 C.6 D.7
(9)若点 A( -2,m)在正比例函数 的图像上 ,则 m 的值是( ) .
C.1 D. -1
(10)已知反比例函数的图像 有两点 A(x1,y1 ) 、B(x2,y2 ) ,若 y1 >y2 ,则 x1 -x2 的值是( ) .
A. 正数 B. 负数 C. 非正数 D. 不能确定
2. 填空题(每题 3 分 ,共 24分)
(1)已知反比例函数 则 自变量 x 的取值范围是 .
(2)若点 M(3,a)关于 y轴的对称点是点 N(b,2) ,则(a+b) 2 024 = .
(3)如图 17-12所示 ,直线 y= 2x+4与 x,y轴分别交于点 A,B两点 , 以 OB为边在 y 轴右侧作等边三 角形 OBC,将点 C向左平移 ,使其对应点 C'恰好落在直线 AB上 ,则点 C'的坐标为 .
(4)小明从家跑步到学校 ,接着马上原路步行回家 . 如图 17-13是小明离家的路程 y(m) 与时间 t(min) 的函数图像 ,则小明回家的速度是每分钟步行 m.
(5)直线 y=3x+2沿 y轴向下平移 5个单位 ,则平移后直线与 y轴的交点坐标为 .
(6)将一次函数 y= 3x- 1 的图像沿 y 轴向上平移 3 个单位后 ,得到的图像 对 应 的 函 数 关 系 式 为
.
(7)如图 17-14所示 , 已知直线 l1 :y=k1x+4与直线 l2 :y=k2x-5交于点 A,它们与 y轴的交点分别为 点 B,C,点 E,F分别为线段 AB,AC的中点,则线段 EF的长度为 .
图 17-12 图 17-13 图 17-14
(8)在反比例函数 的图像的每一条曲线上 ,y都随 x 的增大而减小 ,则 m 的取值范围是
.
3. 解答题(共 46分)
(1)已知某厂现有 A种金属 70t,B种金属 52t,现计划用这两种金属生产 M,N 两种型号的合金产品共 80000套 . 已知做一套 M 型号的合金产品需要 A 种金属 0.6 kg,B种金属 0.9 kg,可获利润 45元 ;做一套 N 种型号的合金产品需要 A种金属 1.1 kg,B种金属 0.4 kg,可获利润 50元 . 若设生产 N 种型号的合金产品 套数为 x,用这批金属生产这两种型号的合金产品所获总利润为 y元 . (6分)
①求 y与 x 的函数关系式 ,并求出 自变量 x 的取值范围 ;
②在生产这批合金产品时 ,N 型号的合金产品应生产多少套 ,该厂所获利润最大 最大利润是多少
2
(2)甲 、乙两支清雪队同时开始清理某路段积雪 ,一段时间后 , 乙队被调往别处 , 甲队又用了 3 h 完成了 剩余的清雪任务 , 已知甲队每小时的清雪量保持不变 , 乙队每小时清雪 50t, 甲 、乙两队在此路段的清雪总量 y(t)与清雪时间 x(时)之间的函数图像如图 17-15所示 . (8分)
①乙队调离时 , 甲 、乙两队已完成的清雪总量为 t.
②求此次任务的清雪总量 m.
③求乙队调离后 y与 x 之间的函数关系式 .
图 17-15
(3)如图 17-16(a)所示 ,长为 60 km 的某线路 AB上有甲 、乙两车 ,分别从南站 A 和北站 B 同时出发相 向而行 ,到达 B,A后立刻返回到出发站停止 ,速度均为 30 km/h. 设甲车 、乙车距南站 A 的路程分别为 y甲 , y乙 (km) ,行驶时间为 t(h) . (8分)
①图 17-16(b)已画出 y甲 与 t的函数图像 ,其中 a= ,b= ,c= ;
②分别写出 0≤t≤2及 2
(a) (b)
图 17-16
3
(4)从甲地到乙地 ,先是一段平路 ,然后是一段上坡路 ,小明骑车从甲地出发 ,到达乙地后立即原路返回 甲地 . 途中休息了一段时间 . 假设小明骑车在平路 、上坡 、下坡时分别保持匀速前进 . 已知小明骑车上坡的速 度比在平路上的速度每小时少 5 km ,下坡的速度比在平路上的速度每小时多 5 km ,设小明出发 x h 后 , 到 达离甲地 y km 的地方 , 图 17-17中的折线 OABCDE 表示 y 与 x 之间的函数关系 . (8分)
①小明骑车在平路上的速度为 km/h;他途中休息了 h.
②求线段 AB,BC所表示的 y 与 x 之间的函数关系式 .
③如果小明两次经过途中某一地点的时间间隔为 0.15 h,那么该地点离甲地多远
图 17-17
(5)已知 A(x1 ,y1 ) ,B (x2,y2 )是反比例函数 图像上的两点,且 x1 - x2 = -2,x1 ·x2 = 3,y1 - y2 . 当 -3
点,BC垂直于 x 轴 ,垂足为 C,△AOC的面积是 1. (8分)
①求 m,n的值 ;
②求直线 AC的函数表达式 .
图 17-18
4
