第 18章 平行四边形 评估检测题(A卷) 单元测试 (无答案)2024-2025学年八年级下册数学华师版
文档属性
| 名称 | 第 18章 平行四边形 评估检测题(A卷) 单元测试 (无答案)2024-2025学年八年级下册数学华师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 75.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 00:00:00 | ||
图片预览


文档简介
第 18章评估检测题(A卷)
(时间 :90分钟 总分 :100分)
1. 选择题(每题 4分 ,共 32分)
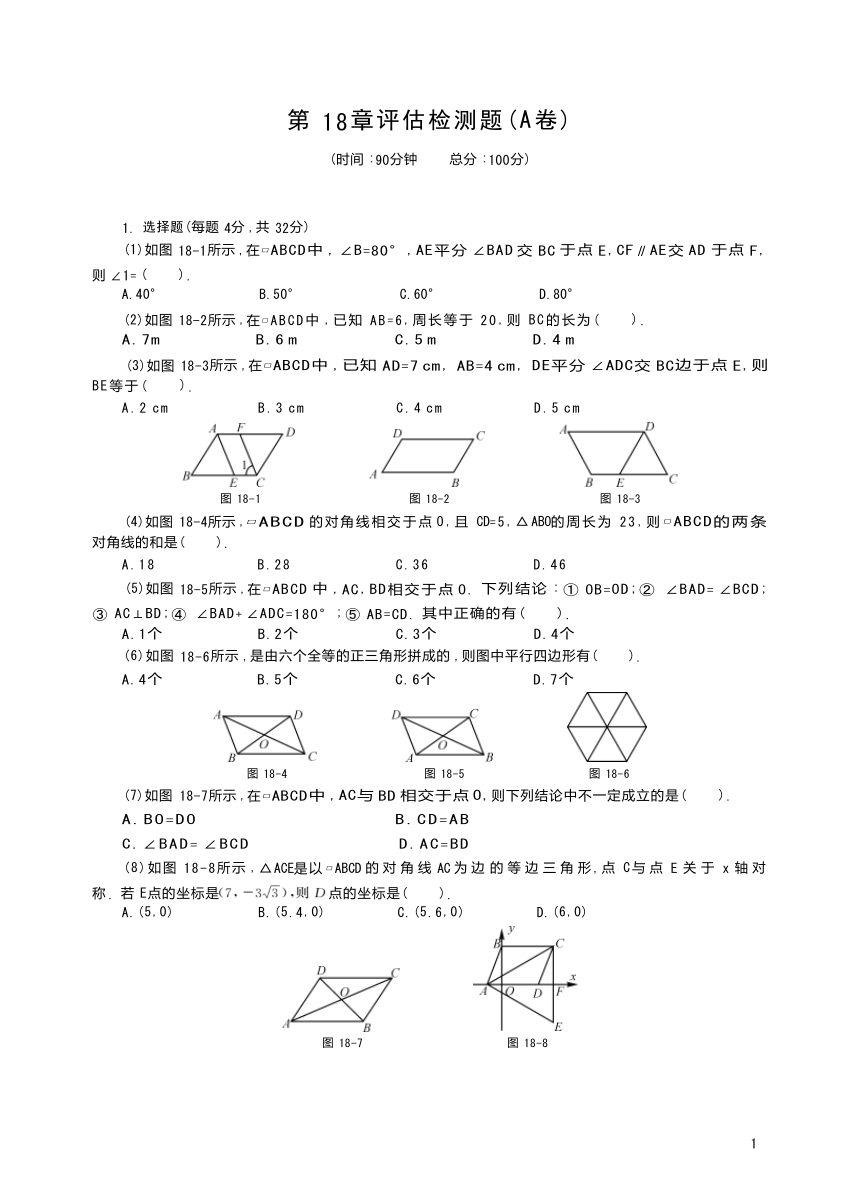
(1)如图 18-1所示 ,在 ABCD中 , ∠B=80°,AE平分 ∠BAD 交 BC 于点 E,CF∥AE交 AD 于点 F, 则 ∠1= ( ).
A.40° B.50° C.60° D.80°
(2)如图 18-2所示 ,在 ABCD中 ,已知 AB=6,周长等于 20,则 BC的长为( ).
A.7m B.6 m C.5 m D.4 m
(3)如图 18-3所示 ,在 ABCD中 ,已知 AD=7 cm, AB=4 cm, DE平分 ∠ADC交 BC边于点 E,则
BE等于( ).
A.2 cm B.3 cm C.4 cm D.5 cm
图 18-1 图 18-2 图 18-3
(4)如图 18-4所示 , ABCD 的对角线相交于点 O,且 CD=5,△ABO的周长为 23,则 ABCD的两条
对角线的和是( ).
A.18 B.28 C.36 D.46
(5)如图 18-5所示 ,在 ABCD 中 ,AC,BD相交于点 O. 下列结论 : ① OB=OD;② ∠BAD= ∠BCD;
③ AC⊥BD;④ ∠BAD+ ∠ADC=180°; ⑤ AB=CD. 其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
(6)如图 18-6所示 ,是由六个全等的正三角形拼成的 ,则图中平行四边形有( ).
A.4个 B.5个 C.6个 D.7个
图 18-4 图 18-5 图 18-6
(7)如图 18-7所示 ,在 ABCD中 ,AC与 BD 相交于点 O,则下列结论中不一定成立的是( ).
A.BO=DO B.CD=AB
C.∠BAD= ∠BCD D.AC=BD
(8)如图 18-8所示 ,△ACE是以 ABCD 的 对 角 线 AC 为 边 的 等 边 三 角 形,点 C与 点 E 关 于 x 轴 对 称 . 若 E点的坐标是点的坐标是( ).
A.(5,0) B.(5.4,0) C.(5.6,0) D.(6,0)
图 18-7 图 18-8
1
2. 填空题(每题 3分 ,共 24分)
(1)如图 18-9所示 ,在 ABCD中 ,点 B关于点 O的对称点是点 .
图 18-9
(
°
)(2)如图 18-10所示 ,在 ABCD中 ,CE⊥AB于 E,若 ∠A=125°,则 ∠BCE= .
图 18-10
(3)如图 18-11所示 ,把一张平行四边形纸 ABCD沿 BD 对折 ,使点 C落在 E 处 ,BE与 AD 相交于 O,
若 ∠DBC=15°,则 ∠BOD= °.
图 18-11
(4)用一根长度为 18 cm 的铁丝围成一个平行四边形 ,各边的长度恰好都是 3 的整数倍 ,则平行四边形 相邻的边长为 .
(5) ABCD的对角线相交于点 O,S△ AOB =3 cm2 ,则 S ABCD = cm2.
(6)如图 18-12所 示 , ABCD 的 对 角 线 AC 与 BD 相 交 于 点 O,其 周 长 为 18,且 △AOB 的 周 长 比 △BOC的周长小 1. 则边 AB和 BC 的长分别为 .
(7)如图 18-13所示 ,在 ABCD中 ,对 角 线 AC= 21 cm,DE⊥AC,垂 足 为 点 E,且 DE= 5 cm,AD= 7 cm. 则 AD和 BC之间的距离为 cm.
(8)如图 18-14所示 ,在四边形 ABCD 中 ,AD∥BC,AD=4,BC=12,E是 BC的中点 . 点 P 以每秒 1个 单位长度的速度从点 A出发 ,沿 AD 向点 D 运动 ;点 Q同时以每秒 2个单位长度的速度从点 C出发 ,沿 CB 向点B 运动 . 点 P停止运动时,点 Q也随之停止运动 . 当运动时间为 s时 ,以点 P,Q,E,D为顶点的
四边形是平行四边形 .
图 18-12 图 18-13 图 18-14
3. 解答题(共 44分)
(1)如图 18-15所示 ,在 △ABC中 ,AB=AC,D,E,F分别是 AC,BC,BA延长线上的点,四边形 ADEF 为平行四边形 ,求证 :AD=BF. (6分)
图 18-15
2
(2)如图 18-16所示 ,在 ABCD中 , ∠B= ∠AFE,EA是 ∠BEF的平分线 ,求证 :(6分)
①△ABE≌△AFE;
②∠FAD= ∠CDE.
图 18-16
(3)如图 18-17所示 ,在 ABCD中 ,点 E,F分别在边 BC和 AD 上 ,且 BE=DF. 求证 :(6分)
①△ABE≌△CDF;
②求证 :AE=CF.
图 18-17
(4)如图 18-18所示,点 A,F,C,D 在同一直线上,点 B和点 E 分别在直线 AD 的两侧 ,且 AB=DE, ∠A= ∠D,AF=DC. (8分)
①请直接写出图中两对全等的三角形 ;
②求证 :四边形 BCEF是平行四边形 .
图 18-18
3
(5)如图 18-19所示 , ABCD 中 ,BD⊥AD, ∠A=45°,E,F分别是 AB,CD上的点,且 BE=DF,连接 EF交 BD 于 O. (8分)
①求证 :BO=DO;
②若 EF⊥AB,延长 EF交 AD 的延长线于 G,当 FG=1时 ,求 AD 的长 .
图 18-19
(6)已知 :如图 18-20所示 ,在 △ABC中 , ∠ACB=90°,D是 BC 的中点,DE⊥BC,CE∥AD. 如果 AC= 2,CE=4. (10分)
①求证 :四边形 ACED是平行四边形 ;
②求四边形 ACEB的周长 ;
③直接写出 CE和 AD之间的距离 .
图 18-20
4
(时间 :90分钟 总分 :100分)
1. 选择题(每题 4分 ,共 32分)
(1)如图 18-1所示 ,在 ABCD中 , ∠B=80°,AE平分 ∠BAD 交 BC 于点 E,CF∥AE交 AD 于点 F, 则 ∠1= ( ).
A.40° B.50° C.60° D.80°
(2)如图 18-2所示 ,在 ABCD中 ,已知 AB=6,周长等于 20,则 BC的长为( ).
A.7m B.6 m C.5 m D.4 m
(3)如图 18-3所示 ,在 ABCD中 ,已知 AD=7 cm, AB=4 cm, DE平分 ∠ADC交 BC边于点 E,则
BE等于( ).
A.2 cm B.3 cm C.4 cm D.5 cm
图 18-1 图 18-2 图 18-3
(4)如图 18-4所示 , ABCD 的对角线相交于点 O,且 CD=5,△ABO的周长为 23,则 ABCD的两条
对角线的和是( ).
A.18 B.28 C.36 D.46
(5)如图 18-5所示 ,在 ABCD 中 ,AC,BD相交于点 O. 下列结论 : ① OB=OD;② ∠BAD= ∠BCD;
③ AC⊥BD;④ ∠BAD+ ∠ADC=180°; ⑤ AB=CD. 其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
(6)如图 18-6所示 ,是由六个全等的正三角形拼成的 ,则图中平行四边形有( ).
A.4个 B.5个 C.6个 D.7个
图 18-4 图 18-5 图 18-6
(7)如图 18-7所示 ,在 ABCD中 ,AC与 BD 相交于点 O,则下列结论中不一定成立的是( ).
A.BO=DO B.CD=AB
C.∠BAD= ∠BCD D.AC=BD
(8)如图 18-8所示 ,△ACE是以 ABCD 的 对 角 线 AC 为 边 的 等 边 三 角 形,点 C与 点 E 关 于 x 轴 对 称 . 若 E点的坐标是点的坐标是( ).
A.(5,0) B.(5.4,0) C.(5.6,0) D.(6,0)
图 18-7 图 18-8
1
2. 填空题(每题 3分 ,共 24分)
(1)如图 18-9所示 ,在 ABCD中 ,点 B关于点 O的对称点是点 .
图 18-9
(
°
)(2)如图 18-10所示 ,在 ABCD中 ,CE⊥AB于 E,若 ∠A=125°,则 ∠BCE= .
图 18-10
(3)如图 18-11所示 ,把一张平行四边形纸 ABCD沿 BD 对折 ,使点 C落在 E 处 ,BE与 AD 相交于 O,
若 ∠DBC=15°,则 ∠BOD= °.
图 18-11
(4)用一根长度为 18 cm 的铁丝围成一个平行四边形 ,各边的长度恰好都是 3 的整数倍 ,则平行四边形 相邻的边长为 .
(5) ABCD的对角线相交于点 O,S△ AOB =3 cm2 ,则 S ABCD = cm2.
(6)如图 18-12所 示 , ABCD 的 对 角 线 AC 与 BD 相 交 于 点 O,其 周 长 为 18,且 △AOB 的 周 长 比 △BOC的周长小 1. 则边 AB和 BC 的长分别为 .
(7)如图 18-13所示 ,在 ABCD中 ,对 角 线 AC= 21 cm,DE⊥AC,垂 足 为 点 E,且 DE= 5 cm,AD= 7 cm. 则 AD和 BC之间的距离为 cm.
(8)如图 18-14所示 ,在四边形 ABCD 中 ,AD∥BC,AD=4,BC=12,E是 BC的中点 . 点 P 以每秒 1个 单位长度的速度从点 A出发 ,沿 AD 向点 D 运动 ;点 Q同时以每秒 2个单位长度的速度从点 C出发 ,沿 CB 向点B 运动 . 点 P停止运动时,点 Q也随之停止运动 . 当运动时间为 s时 ,以点 P,Q,E,D为顶点的
四边形是平行四边形 .
图 18-12 图 18-13 图 18-14
3. 解答题(共 44分)
(1)如图 18-15所示 ,在 △ABC中 ,AB=AC,D,E,F分别是 AC,BC,BA延长线上的点,四边形 ADEF 为平行四边形 ,求证 :AD=BF. (6分)
图 18-15
2
(2)如图 18-16所示 ,在 ABCD中 , ∠B= ∠AFE,EA是 ∠BEF的平分线 ,求证 :(6分)
①△ABE≌△AFE;
②∠FAD= ∠CDE.
图 18-16
(3)如图 18-17所示 ,在 ABCD中 ,点 E,F分别在边 BC和 AD 上 ,且 BE=DF. 求证 :(6分)
①△ABE≌△CDF;
②求证 :AE=CF.
图 18-17
(4)如图 18-18所示,点 A,F,C,D 在同一直线上,点 B和点 E 分别在直线 AD 的两侧 ,且 AB=DE, ∠A= ∠D,AF=DC. (8分)
①请直接写出图中两对全等的三角形 ;
②求证 :四边形 BCEF是平行四边形 .
图 18-18
3
(5)如图 18-19所示 , ABCD 中 ,BD⊥AD, ∠A=45°,E,F分别是 AB,CD上的点,且 BE=DF,连接 EF交 BD 于 O. (8分)
①求证 :BO=DO;
②若 EF⊥AB,延长 EF交 AD 的延长线于 G,当 FG=1时 ,求 AD 的长 .
图 18-19
(6)已知 :如图 18-20所示 ,在 △ABC中 , ∠ACB=90°,D是 BC 的中点,DE⊥BC,CE∥AD. 如果 AC= 2,CE=4. (10分)
①求证 :四边形 ACED是平行四边形 ;
②求四边形 ACEB的周长 ;
③直接写出 CE和 AD之间的距离 .
图 18-20
4
