第 20章 数据的整理与初步处理 评估检测题(A卷) 单元测试 (无答案)2024-2025学年八年级下册数学华师版
文档属性
| 名称 | 第 20章 数据的整理与初步处理 评估检测题(A卷) 单元测试 (无答案)2024-2025学年八年级下册数学华师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 68.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 20:39:13 | ||
图片预览


文档简介
第 20章评估检测题(A卷)
(时间 :90分钟 总分 :100分)
1. 选择题(每题 3 分 ,共 24分)
(1)我省某市五月份第二周连续七天的空气质量指数分别为 : 111, 96,47, 68, 70, 77, 105,则这七天空气 质量指数的平均数是( ) .
A.71.8 B.77 C.82 D.95.7
(2)在一次 “爱心互助 ”捐款活动中 ,某班第一小组 8名同学捐款的金额(单位 :元)如下表所示 .
金额/元 5 6 7 10
人数/人 2 3 2 1
这 8名同学捐款的平均金额为( ) .
A.3.5元 B.6元 C.6.5元 D.7元
(3)一组数据 6, -3,0,1,6 的中位数是( ) .
A.0 B.1 C.2 D.6
(4)下列选项中 ,显示部分在总体中所占百分比的统计图是( ) .
A. 扇形图 B. 条形图 C. 折线图 D. 直方图
(5)某班组织了一次读书活动 ,统计了 10名同学在一周内的读书时间 ,他们一周内的读书时间累计如下 表 ,则这 10名同学在一周内累计读书时间的中位数是( ) .
一周 内 累计的读书时间/h 5 8 10 14
人数/人 1 4 3 2
A.8 B.7 C.9 D.10
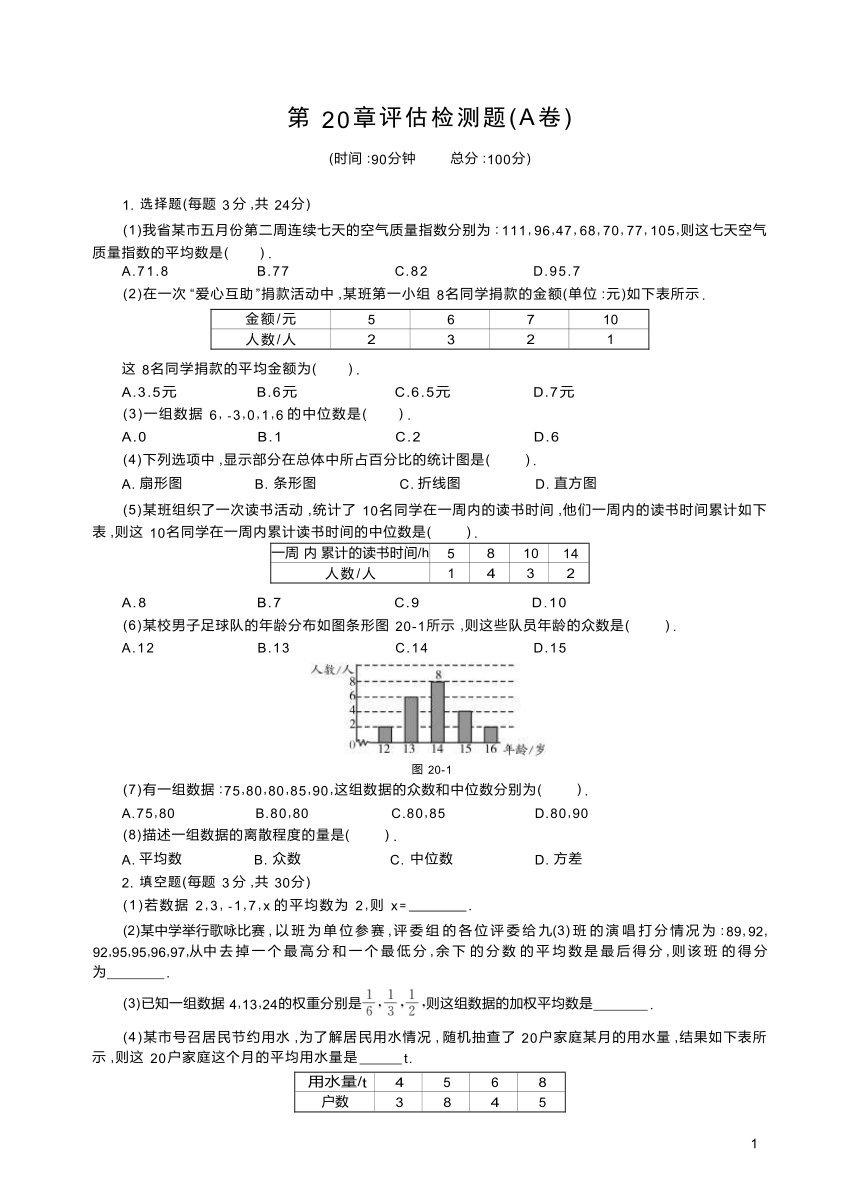
(6)某校男子足球队的年龄分布如图条形图 20-1所示 ,则这些队员年龄的众数是( ) .
A.12 B.13 C.14 D.15
图 20-1
(7)有一组数据 :75,80,80,85,90,这组数据的众数和中位数分别为( ) .
A.75,80 B.80,80 C.80,85 D.80,90
(8)描述一组数据的离散程度的量是( ) .
A. 平均数 B. 众数 C. 中位数 D. 方差
2. 填空题(每题 3 分 ,共 30分)
(1)若数据 2,3, -1,7,x 的平均数为 2,则 x= .
(2)某中学举行歌咏比赛 , 以 班 为 单 位 参 赛 , 评 委 组 的 各 位 评 委 给 九(3) 班 的 演 唱 打 分 情 况 为 : 89, 92, 92,95,95,96,97,从中 去 掉 一 个 最 高 分 和 一 个 最 低 分 , 余 下 的 分 数 的 平 均 数 是 最 后 得 分 , 则 该 班 的 得 分 为 .
(3)已知一组数据 4,13,24的权重分别是则这组数据的加权平均数是 .
(4)某市号召居民节约用水 ,为了解居民用水情况 , 随机抽查了 20户家庭某月的用水量 ,结果如下表所 示 ,则这 20户家庭这个月的平均用水量是 t.
用水量/t 4 5 6 8
户数 3 8 4 5
1
(5)在一次数学测验中 , 随机抽取了 10份试卷 ,其成绩如下 :85,81,89,81, 72,82, 77,81, 79,83. 则这组 数据的中位数为 .
(6)两组数据 :3,a,2b,5 与 a,6,b的平均数都是 6,若将这两组数据合并为一组数据 ,则这组新数据的中 位数为 .
(7)高一新生入学军训射击训练中 ,小张同学的射击成绩(单位 :环)为 :5,7,9, 10, 7,则这组数据的众数 是 .
(8) “植树节 ”时 ,九年级(1)班 6个小组的植树棵数分别是 : 5, 7,3,x,6,4. 已知这组数据的众数是 5,则 该组数据的平均数是 .
(9)若数据 1,2,x,4 的众数是 1,则这组数据的方差为 .
(10)下表是在某市某一天不同时段测得的气温情况 .
时间 0:00 4:00 8:00 12:00 16:00 18:00
气温/℃ 25 27 29 32 34 30
则这一天气温的温差是 ℃ .
3. 解答题(共 46分)
(1)某校为了招聘一名优秀教师 ,对入选的三名候选人进行教学技能与专业知识两种考核 ,现将甲 、乙 、 丙三人的考核成绩统计如下表(百分制) . (8分)
候选人 教学技能考核成绩 专业知识考核成绩
甲 85 92
乙 91 85
丙 80 90
①如果校方认为教师的教学技能水平与专业知识水平同等重要 ,则候选人 将被录取 .
②如果校方认为教师的教学技能水平比专业知识水平重要 , 因此分别赋予它们 6 和 4 的权 . 计算他们赋 权后各自的平均成绩 ,并说明谁将被录取 .
(2)作为宁波市政府民生实事之一的公共自行车建设工作已基本完成 ,某部门对今年 4 月份的 7 天进行 了公共自行车日租车量的统计 ,结果如图 20-2所示 . (8分)
图 20-2
①求这 7 天日租车量的众数 、中位数和平均数 ;
②用 ①中的平均数估计 4 月份(30天)共租车多少万车次 .
2
(3)某校为了选拔学生参加 “汉字听写大赛 ”,对九年级(1)班 、(2)班各 10名学生进行汉字听写测试 ,计 分采用 10分制(得分均取整数) ,成绩达到 6分或 6 分以上为及格 ,达到 9 分或 10分为优秀 . 成绩如表 1 所 示 ,并制作了表 2成绩分析表 . (10分)
表 1
(1) 班 5 8 8 9 8 10 10 8 5 5
(2) 班 10 6 6 9 10 4 5 7 10 8
表 2
班级 平均分 中位数 众数 方差 及格率 优秀率
(1) 班 7.6 8 a 3.82 70% 30%
(2) 班 b 7.5 10 4.94 80% 40%
①在表 2 中 ,a= ,b= ;
②有人说二班的及格率 、优秀率均高于一班 ,所以二班成绩比一班成绩好 ;但也有人坚定认为一班成绩 比二班成绩好 . 请你给出支持一班成绩好的两条理由 .
(4)要从甲 , 乙两名同学中选出一名 ,代表班级参加射击比赛 . 两人最近 10次射击训练成绩的折线统计 图如图 20-3所示 . (10分)
图 20-3
①已求得甲的平均数成绩为 8环 ,求乙的平均成绩 ;
②观察统计图 ,直接写出甲 , 乙这 10次射击成绩的方差 s ,s 哪个大 ;
③如果其他班级参赛选手的射击成绩都在 7环左右 ,本班应该选 参赛更适合 ;如果其他班级参 赛选手的射击成绩都在 9环左右 ,本班应该选 参赛更适合 .
3
(5)某市 2010-2014年社会消费品零售总额及增速统计如图 20-4所示 . (10分)
某市社会消费品总额统计图 某市社会消费品零售增速统计图
(a) (b)
图 20-4
请根据图中信息 ,解答下列问题 :
①求该市 2010-2014年社会消费品零售总额增速这组数据的中位数 ;
②求该市近三年(2012-2014年)的社会消费品零售总额这组数据的平均数 ;
③用适当的方法预测该市 2015年社会消费品总额 . (只要求列出算式 , 不必计算出结果)
4
(时间 :90分钟 总分 :100分)
1. 选择题(每题 3 分 ,共 24分)
(1)我省某市五月份第二周连续七天的空气质量指数分别为 : 111, 96,47, 68, 70, 77, 105,则这七天空气 质量指数的平均数是( ) .
A.71.8 B.77 C.82 D.95.7
(2)在一次 “爱心互助 ”捐款活动中 ,某班第一小组 8名同学捐款的金额(单位 :元)如下表所示 .
金额/元 5 6 7 10
人数/人 2 3 2 1
这 8名同学捐款的平均金额为( ) .
A.3.5元 B.6元 C.6.5元 D.7元
(3)一组数据 6, -3,0,1,6 的中位数是( ) .
A.0 B.1 C.2 D.6
(4)下列选项中 ,显示部分在总体中所占百分比的统计图是( ) .
A. 扇形图 B. 条形图 C. 折线图 D. 直方图
(5)某班组织了一次读书活动 ,统计了 10名同学在一周内的读书时间 ,他们一周内的读书时间累计如下 表 ,则这 10名同学在一周内累计读书时间的中位数是( ) .
一周 内 累计的读书时间/h 5 8 10 14
人数/人 1 4 3 2
A.8 B.7 C.9 D.10
(6)某校男子足球队的年龄分布如图条形图 20-1所示 ,则这些队员年龄的众数是( ) .
A.12 B.13 C.14 D.15
图 20-1
(7)有一组数据 :75,80,80,85,90,这组数据的众数和中位数分别为( ) .
A.75,80 B.80,80 C.80,85 D.80,90
(8)描述一组数据的离散程度的量是( ) .
A. 平均数 B. 众数 C. 中位数 D. 方差
2. 填空题(每题 3 分 ,共 30分)
(1)若数据 2,3, -1,7,x 的平均数为 2,则 x= .
(2)某中学举行歌咏比赛 , 以 班 为 单 位 参 赛 , 评 委 组 的 各 位 评 委 给 九(3) 班 的 演 唱 打 分 情 况 为 : 89, 92, 92,95,95,96,97,从中 去 掉 一 个 最 高 分 和 一 个 最 低 分 , 余 下 的 分 数 的 平 均 数 是 最 后 得 分 , 则 该 班 的 得 分 为 .
(3)已知一组数据 4,13,24的权重分别是则这组数据的加权平均数是 .
(4)某市号召居民节约用水 ,为了解居民用水情况 , 随机抽查了 20户家庭某月的用水量 ,结果如下表所 示 ,则这 20户家庭这个月的平均用水量是 t.
用水量/t 4 5 6 8
户数 3 8 4 5
1
(5)在一次数学测验中 , 随机抽取了 10份试卷 ,其成绩如下 :85,81,89,81, 72,82, 77,81, 79,83. 则这组 数据的中位数为 .
(6)两组数据 :3,a,2b,5 与 a,6,b的平均数都是 6,若将这两组数据合并为一组数据 ,则这组新数据的中 位数为 .
(7)高一新生入学军训射击训练中 ,小张同学的射击成绩(单位 :环)为 :5,7,9, 10, 7,则这组数据的众数 是 .
(8) “植树节 ”时 ,九年级(1)班 6个小组的植树棵数分别是 : 5, 7,3,x,6,4. 已知这组数据的众数是 5,则 该组数据的平均数是 .
(9)若数据 1,2,x,4 的众数是 1,则这组数据的方差为 .
(10)下表是在某市某一天不同时段测得的气温情况 .
时间 0:00 4:00 8:00 12:00 16:00 18:00
气温/℃ 25 27 29 32 34 30
则这一天气温的温差是 ℃ .
3. 解答题(共 46分)
(1)某校为了招聘一名优秀教师 ,对入选的三名候选人进行教学技能与专业知识两种考核 ,现将甲 、乙 、 丙三人的考核成绩统计如下表(百分制) . (8分)
候选人 教学技能考核成绩 专业知识考核成绩
甲 85 92
乙 91 85
丙 80 90
①如果校方认为教师的教学技能水平与专业知识水平同等重要 ,则候选人 将被录取 .
②如果校方认为教师的教学技能水平比专业知识水平重要 , 因此分别赋予它们 6 和 4 的权 . 计算他们赋 权后各自的平均成绩 ,并说明谁将被录取 .
(2)作为宁波市政府民生实事之一的公共自行车建设工作已基本完成 ,某部门对今年 4 月份的 7 天进行 了公共自行车日租车量的统计 ,结果如图 20-2所示 . (8分)
图 20-2
①求这 7 天日租车量的众数 、中位数和平均数 ;
②用 ①中的平均数估计 4 月份(30天)共租车多少万车次 .
2
(3)某校为了选拔学生参加 “汉字听写大赛 ”,对九年级(1)班 、(2)班各 10名学生进行汉字听写测试 ,计 分采用 10分制(得分均取整数) ,成绩达到 6分或 6 分以上为及格 ,达到 9 分或 10分为优秀 . 成绩如表 1 所 示 ,并制作了表 2成绩分析表 . (10分)
表 1
(1) 班 5 8 8 9 8 10 10 8 5 5
(2) 班 10 6 6 9 10 4 5 7 10 8
表 2
班级 平均分 中位数 众数 方差 及格率 优秀率
(1) 班 7.6 8 a 3.82 70% 30%
(2) 班 b 7.5 10 4.94 80% 40%
①在表 2 中 ,a= ,b= ;
②有人说二班的及格率 、优秀率均高于一班 ,所以二班成绩比一班成绩好 ;但也有人坚定认为一班成绩 比二班成绩好 . 请你给出支持一班成绩好的两条理由 .
(4)要从甲 , 乙两名同学中选出一名 ,代表班级参加射击比赛 . 两人最近 10次射击训练成绩的折线统计 图如图 20-3所示 . (10分)
图 20-3
①已求得甲的平均数成绩为 8环 ,求乙的平均成绩 ;
②观察统计图 ,直接写出甲 , 乙这 10次射击成绩的方差 s ,s 哪个大 ;
③如果其他班级参赛选手的射击成绩都在 7环左右 ,本班应该选 参赛更适合 ;如果其他班级参 赛选手的射击成绩都在 9环左右 ,本班应该选 参赛更适合 .
3
(5)某市 2010-2014年社会消费品零售总额及增速统计如图 20-4所示 . (10分)
某市社会消费品总额统计图 某市社会消费品零售增速统计图
(a) (b)
图 20-4
请根据图中信息 ,解答下列问题 :
①求该市 2010-2014年社会消费品零售总额增速这组数据的中位数 ;
②求该市近三年(2012-2014年)的社会消费品零售总额这组数据的平均数 ;
③用适当的方法预测该市 2015年社会消费品总额 . (只要求列出算式 , 不必计算出结果)
4
