9.3.1 图形的旋转 教案 华师大版(2024)数学七年级下册
文档属性
| 名称 | 9.3.1 图形的旋转 教案 华师大版(2024)数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 774.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览

文档简介
9.3 旋 转
1.图形的旋转
1.了解图形旋转变换的意义.
2.理解旋转中心在旋转过程中保持不动,图形的旋转由旋转中心和旋转角度决定.(重点)
3.观察图形,判断两个图形是否能通过旋转后重合,以及旋转中心和旋转角度的识别.(难点)
一、新课导入
[情境导入]在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的旋转现象.生活中的这些现象有什么共同特点?(课件动态展示)
二、新知探究
知识点:图形的旋转及其有关概念
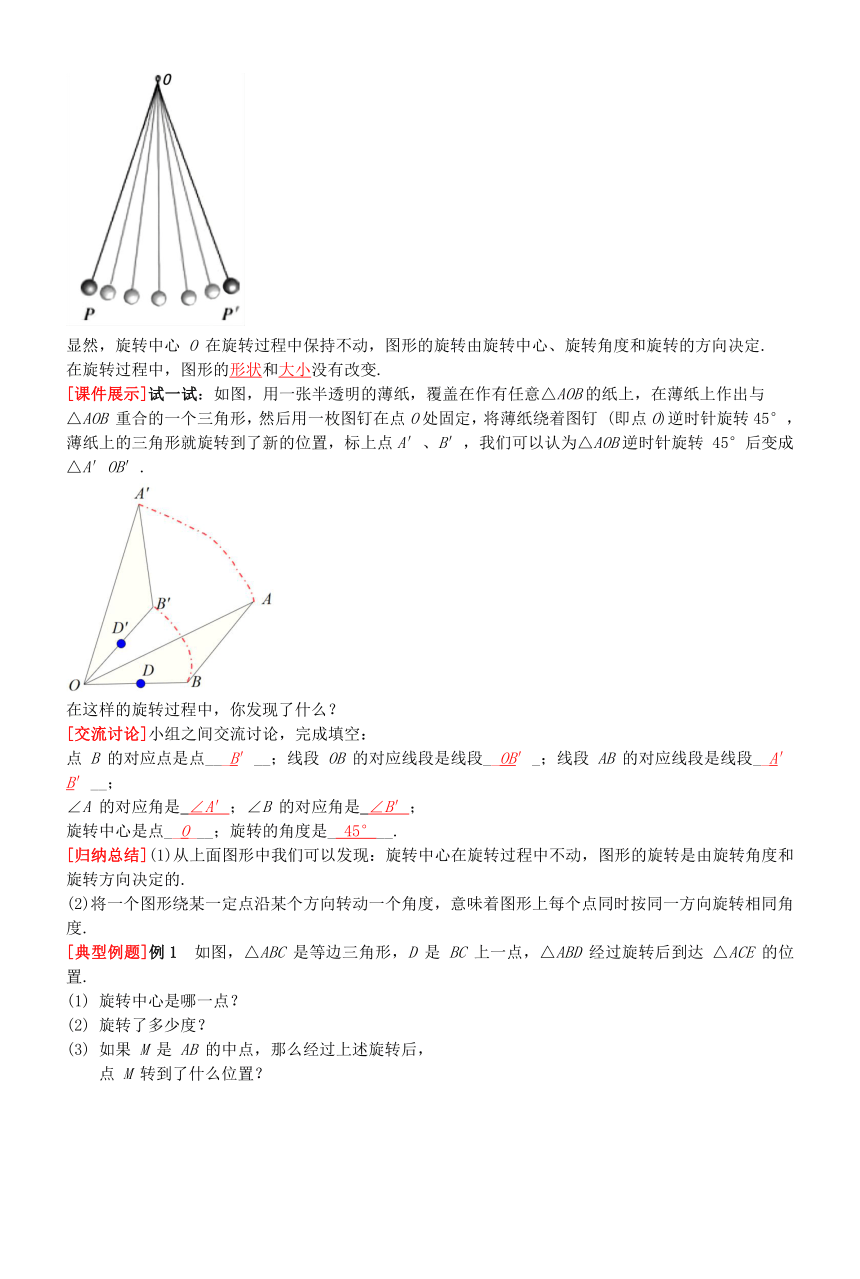
[课件展示]如图,单摆上小球的转动,由位置P转到位置P′,像这样的运动就叫做旋转,这个悬挂点O就叫做小球旋转的旋转中心.
显然,旋转中心 O 在旋转过程中保持不动,图形的旋转由旋转中心、旋转角度和旋转的方向决定.
在旋转过程中,图形的形状和大小没有改变.
[课件展示]试一试:如图,用一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与
△AOB 重合的一个三角形,然后用一枚图钉在点O处固定,将薄纸绕着图钉 (即点O)逆时针旋转45°,薄纸上的三角形就旋转到了新的位置,标上点A′、B′,我们可以认为△AOB逆时针旋转 45°后变成△A′OB′.
在这样的旋转过程中,你发现了什么?
[交流讨论]小组之间交流讨论,完成填空:
点 B 的对应点是点___B′__;线段 OB 的对应线段是线段__OB′_;线段 AB 的对应线段是线段__A′B′__;
∠A 的对应角是 ∠A′;∠B 的对应角是 ∠B′;
旋转中心是点__O___;旋转的角度是_ 45°__.
[归纳总结](1)从上面图形中我们可以发现:旋转中心在旋转过程中不动,图形的旋转是由旋转角度和旋转方向决定的.
(2)将一个图形绕某一定点沿某个方向转动一个角度,意味着图形上每个点同时按同一方向旋转相同角度.
[典型例题]例1 如图,△ABC 是等边三角形,D 是 BC 上一点,△ABD 经过旋转后到达 △ACE 的位置.
(1) 旋转中心是哪一点?
(2) 旋转了多少度?
(3) 如果 M 是 AB 的中点,那么经过上述旋转后,
点 M 转到了什么位置?
解: (1) 旋转中心是点 A.
(2) 旋转了 60°.
(3) 点 M 转到了 AC 的中点位置上.
[典型例题]例2 如图 (1) ,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针方向旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢?
解:如图 (2),顺时针旋转 90°,A'B' 与 AB 互相垂直.
如图 (3),逆时针旋转 90°,A'B' 与 AB 互相垂直.
三、课堂小结
四、课堂训练
1.下列运动形式属于旋转的是( B )
A.飞驰的动车 B.匀速转动的摩天轮
C.运动员投掷标枪 D.乘坐升降电梯
2.如图,若叶片A绕O顺时针旋转到叶片B,则旋转中心是__O__,旋转角是__∠AOB___,旋转角等于__60 _度 .
3.如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置.
(1)指出它的旋转中心;
(2)说出它的旋转方向和旋转角是多少度;
(3)分别写出点A、B、C的对应点.
解:(1)它的旋转中心为点A.
(2)它的旋转方向为逆时针方向,旋转角是45度.
(3)点A、B、C的对应点分别为点A、E、F.
五、布置作业
本节课通过对日常生活的观察,引入旋转的概念,进一步研究构成旋转的三要素,会找出旋转前后的对应点、对应角、对应线段,并解决与旋转相关的数学问题,在探索的过程中知识与能力逐步得到提升,更体现了数学来源于生活并服务于生活的理念.
1.图形的旋转
1.了解图形旋转变换的意义.
2.理解旋转中心在旋转过程中保持不动,图形的旋转由旋转中心和旋转角度决定.(重点)
3.观察图形,判断两个图形是否能通过旋转后重合,以及旋转中心和旋转角度的识别.(难点)
一、新课导入
[情境导入]在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的旋转现象.生活中的这些现象有什么共同特点?(课件动态展示)
二、新知探究
知识点:图形的旋转及其有关概念
[课件展示]如图,单摆上小球的转动,由位置P转到位置P′,像这样的运动就叫做旋转,这个悬挂点O就叫做小球旋转的旋转中心.
显然,旋转中心 O 在旋转过程中保持不动,图形的旋转由旋转中心、旋转角度和旋转的方向决定.
在旋转过程中,图形的形状和大小没有改变.
[课件展示]试一试:如图,用一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与
△AOB 重合的一个三角形,然后用一枚图钉在点O处固定,将薄纸绕着图钉 (即点O)逆时针旋转45°,薄纸上的三角形就旋转到了新的位置,标上点A′、B′,我们可以认为△AOB逆时针旋转 45°后变成△A′OB′.
在这样的旋转过程中,你发现了什么?
[交流讨论]小组之间交流讨论,完成填空:
点 B 的对应点是点___B′__;线段 OB 的对应线段是线段__OB′_;线段 AB 的对应线段是线段__A′B′__;
∠A 的对应角是 ∠A′;∠B 的对应角是 ∠B′;
旋转中心是点__O___;旋转的角度是_ 45°__.
[归纳总结](1)从上面图形中我们可以发现:旋转中心在旋转过程中不动,图形的旋转是由旋转角度和旋转方向决定的.
(2)将一个图形绕某一定点沿某个方向转动一个角度,意味着图形上每个点同时按同一方向旋转相同角度.
[典型例题]例1 如图,△ABC 是等边三角形,D 是 BC 上一点,△ABD 经过旋转后到达 △ACE 的位置.
(1) 旋转中心是哪一点?
(2) 旋转了多少度?
(3) 如果 M 是 AB 的中点,那么经过上述旋转后,
点 M 转到了什么位置?
解: (1) 旋转中心是点 A.
(2) 旋转了 60°.
(3) 点 M 转到了 AC 的中点位置上.
[典型例题]例2 如图 (1) ,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针方向旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢?
解:如图 (2),顺时针旋转 90°,A'B' 与 AB 互相垂直.
如图 (3),逆时针旋转 90°,A'B' 与 AB 互相垂直.
三、课堂小结
四、课堂训练
1.下列运动形式属于旋转的是( B )
A.飞驰的动车 B.匀速转动的摩天轮
C.运动员投掷标枪 D.乘坐升降电梯
2.如图,若叶片A绕O顺时针旋转到叶片B,则旋转中心是__O__,旋转角是__∠AOB___,旋转角等于__60 _度 .
3.如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置.
(1)指出它的旋转中心;
(2)说出它的旋转方向和旋转角是多少度;
(3)分别写出点A、B、C的对应点.
解:(1)它的旋转中心为点A.
(2)它的旋转方向为逆时针方向,旋转角是45度.
(3)点A、B、C的对应点分别为点A、E、F.
五、布置作业
本节课通过对日常生活的观察,引入旋转的概念,进一步研究构成旋转的三要素,会找出旋转前后的对应点、对应角、对应线段,并解决与旋转相关的数学问题,在探索的过程中知识与能力逐步得到提升,更体现了数学来源于生活并服务于生活的理念.
