9.4 中心对称 教案 华师大版(2024)数学七年级下册
文档属性
| 名称 | 9.4 中心对称 教案 华师大版(2024)数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 665.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 00:00:00 | ||
图片预览

文档简介
第9章 轴对称、平移与旋转
9.4 中心对称
1.理解中心对称的定义,掌握中心对称的性质.(重点)
2.培养观察、分析和归纳能力,感受中心对称美,发掘作图能力.(重点)
一、新课导入
[复习导入]在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.
它们的旋转角度分别是多少?
二、新知探究
(一)中心对称图形的认识
[提出问题]问题1:将下面的图形绕 O 点旋转,你有什么发现?
共同点:(1) 都绕一点旋转了180°;(2) 都与原图形完全重合.
[归纳总结]若一个图形绕着中心旋转180°后能与自身重合,我们把这种图形叫做中心对称图形.这个中心叫做对称中心.所以,中心对称图形是旋转角度为180°的旋转对称图形.
你能举出一些这样的实例吗?
[课件展示]
如下面冬天的雪花,太极的图案,还有一些商标等都是中心对称图形.
[提出问题]问题2:观察下列图形的运动,说一说它们有什么共同点.
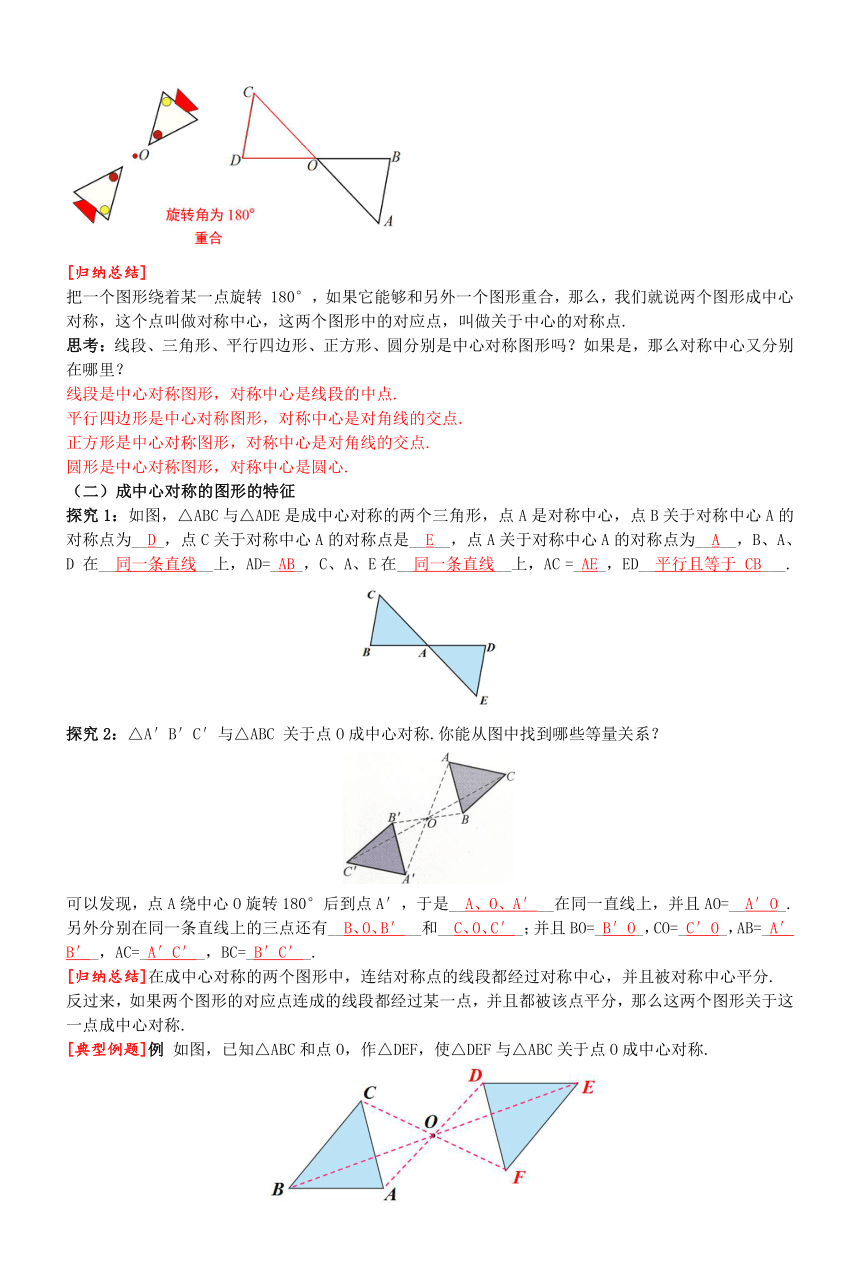
[归纳总结]
把一个图形绕着某一点旋转 180°,如果它能够和另外一个图形重合,那么,我们就说两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
思考:线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗?如果是,那么对称中心又分别在哪里?
线段是中心对称图形,对称中心是线段的中点.
平行四边形是中心对称图形,对称中心是对角线的交点.
正方形是中心对称图形,对称中心是对角线的交点.
圆形是中心对称图形,对称中心是圆心.
(二)成中心对称的图形的特征
探究1:如图,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,点B关于对称中心A的对称点为__D_,点C关于对称中心A的对称点是__E__,点A关于对称中心A的对称点为__A__,B、A、D 在__同一条直线__上,AD=_AB_,C、A、E在__同一条直线__上,AC =_AE_,ED__平行且等于 CB___.
探究2:△A′B′C′与△ABC 关于点O成中心对称.你能从图中找到哪些等量关系?
可以发现,点A绕中心O旋转180°后到点A′,于是__A、O、A′__在同一直线上,并且AO=__A′O_.另外分别在同一条直线上的三点还有__B、O、B′__和__C、O、C′_;并且BO=_B′O_,CO=_C′O_,AB=_A′B′_,AC=_A′C′_,BC=_B′C′_.
[归纳总结]在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
[典型例题]例 如图,已知△ABC和点O,作△DEF,使△DEF与△ABC关于点O成中心对称.
解:(1) 连结AO并延长AO到点D,使OD = OA,于是得到点A关于点O的对称点D;
(2)同样作出点B和点C关于点O的对称点E和F;
(3)顺次连结DE、EF、FD.如图,△DFF即为所求的三角形.
试一试:如图,已知 △ABC 与 △A′B′C′ 中心对称,找出它们的对称中心 O.
解法1:根据观察,B、B′应是对应点,连接 BB′,用刻度尺找出 BB′的中点 O,则点 O 即为所求(如图).
解法2:根据观察,B、B′及 C、C′应是两组对应点,连接 BB′、CC′,BB′、CC′相交于点 O,则点 O 即为所求(如图).
[归纳总结]填写下表:
中心对称与轴对称的异同
三、课堂小结
四、课堂训练
1.如下所示的4组图形中,左边数字与右边数字成中心对称的有( C )
A.1组 B.2组 C.3组 D.4组
2.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( B )
A.2 B.4 C.6 D.8
3. 如图,已知等边三角形 ABC 和点 O,画△A′B′C′,使△A′B′C′ 和 △ABC 关于点 O 成中心对称.
解:如图,△A′B′C′即为所求.
4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形 A′B′C′D′和四边形ABCD关于点O成中心对称.
解:如图,四边形A′B′C′D′即为所求.
五、布置作业
教学过程中,强调学生自主探索和合作交流,结合图形的旋转学习中心对称,体会图形变换思想方法,从类比中感受两者的异同,加深对知识的掌握,要总结中心对称图形和轴对称图形、成中心对称的区别,能够通过作图和联系生活实际进一步感受数学几何问题的趣味性.
9.4 中心对称
1.理解中心对称的定义,掌握中心对称的性质.(重点)
2.培养观察、分析和归纳能力,感受中心对称美,发掘作图能力.(重点)
一、新课导入
[复习导入]在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.
它们的旋转角度分别是多少?
二、新知探究
(一)中心对称图形的认识
[提出问题]问题1:将下面的图形绕 O 点旋转,你有什么发现?
共同点:(1) 都绕一点旋转了180°;(2) 都与原图形完全重合.
[归纳总结]若一个图形绕着中心旋转180°后能与自身重合,我们把这种图形叫做中心对称图形.这个中心叫做对称中心.所以,中心对称图形是旋转角度为180°的旋转对称图形.
你能举出一些这样的实例吗?
[课件展示]
如下面冬天的雪花,太极的图案,还有一些商标等都是中心对称图形.
[提出问题]问题2:观察下列图形的运动,说一说它们有什么共同点.
[归纳总结]
把一个图形绕着某一点旋转 180°,如果它能够和另外一个图形重合,那么,我们就说两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
思考:线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗?如果是,那么对称中心又分别在哪里?
线段是中心对称图形,对称中心是线段的中点.
平行四边形是中心对称图形,对称中心是对角线的交点.
正方形是中心对称图形,对称中心是对角线的交点.
圆形是中心对称图形,对称中心是圆心.
(二)成中心对称的图形的特征
探究1:如图,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,点B关于对称中心A的对称点为__D_,点C关于对称中心A的对称点是__E__,点A关于对称中心A的对称点为__A__,B、A、D 在__同一条直线__上,AD=_AB_,C、A、E在__同一条直线__上,AC =_AE_,ED__平行且等于 CB___.
探究2:△A′B′C′与△ABC 关于点O成中心对称.你能从图中找到哪些等量关系?
可以发现,点A绕中心O旋转180°后到点A′,于是__A、O、A′__在同一直线上,并且AO=__A′O_.另外分别在同一条直线上的三点还有__B、O、B′__和__C、O、C′_;并且BO=_B′O_,CO=_C′O_,AB=_A′B′_,AC=_A′C′_,BC=_B′C′_.
[归纳总结]在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
[典型例题]例 如图,已知△ABC和点O,作△DEF,使△DEF与△ABC关于点O成中心对称.
解:(1) 连结AO并延长AO到点D,使OD = OA,于是得到点A关于点O的对称点D;
(2)同样作出点B和点C关于点O的对称点E和F;
(3)顺次连结DE、EF、FD.如图,△DFF即为所求的三角形.
试一试:如图,已知 △ABC 与 △A′B′C′ 中心对称,找出它们的对称中心 O.
解法1:根据观察,B、B′应是对应点,连接 BB′,用刻度尺找出 BB′的中点 O,则点 O 即为所求(如图).
解法2:根据观察,B、B′及 C、C′应是两组对应点,连接 BB′、CC′,BB′、CC′相交于点 O,则点 O 即为所求(如图).
[归纳总结]填写下表:
中心对称与轴对称的异同
三、课堂小结
四、课堂训练
1.如下所示的4组图形中,左边数字与右边数字成中心对称的有( C )
A.1组 B.2组 C.3组 D.4组
2.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( B )
A.2 B.4 C.6 D.8
3. 如图,已知等边三角形 ABC 和点 O,画△A′B′C′,使△A′B′C′ 和 △ABC 关于点 O 成中心对称.
解:如图,△A′B′C′即为所求.
4.如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形 A′B′C′D′和四边形ABCD关于点O成中心对称.
解:如图,四边形A′B′C′D′即为所求.
五、布置作业
教学过程中,强调学生自主探索和合作交流,结合图形的旋转学习中心对称,体会图形变换思想方法,从类比中感受两者的异同,加深对知识的掌握,要总结中心对称图形和轴对称图形、成中心对称的区别,能够通过作图和联系生活实际进一步感受数学几何问题的趣味性.
