7.4 解一元一次不等式组 教案 华师大版(2024)数学七年级下册
文档属性
| 名称 | 7.4 解一元一次不等式组 教案 华师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 11:26:19 | ||
图片预览


文档简介
7.4 解一元一次不等式组
第1课时 一元一次不等式组及其解法(1)
1.通过具体操作,在解一元一次不等式组的过程
中形成正确的解不等式组的思路与方法.(重点、难点)
2.能够将一元一次不等式组的解集在数轴上正确表示.
一、新课导入
[情境导入]
1.同学们,你能根据上图对话片段估计出这头大象的体重范围吗 请说说你的理由.
2.若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
x≥3① x<5②
二、新知探究
(一)一元一次不等式组的定义
[合作探究]
问题 某工程队用每小时可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,求将污水抽完所用时间的范围.
解:设用xh将污水抽完,则x同时满足不等式
30x>1200,① 30x<1500.②
类比方程组和不等式组
类似于方程组,把这两个含有同一个未知数的一元一次不等式合起来,组成一个一元一次不等式组,记作
[归纳总结]
把两个(或两个以上)含有相同未知数的一元一次不等式合在一起,就得到一个一元一次不等式组.
[针对练习]判断下列不等式组是否为一元一次不等式组.
解:(1)× (2)√ (3)× (4)√
(二)一元一次不等式组的解集
思考 怎样确定上面的不等式组中x的取值范围呢?
类似方程组的解,不等式组中的各不等式解集的公共部分,就是不等式组中x的取值范围.
由不等式①,解得x>40.
由不等式②,解得x<50.
把不等式①和②的解集在数轴上表示出来(如图).
从图容易看出,x取值的范围为40<x<50.
这就是说,将污水抽完所用时间多于40h而少于50h.
[归纳总结]
不等式组中几个不等式的解集的公共部分,叫做这个不等式组的解集.解不等式组就是求它的解集.
备注:利用数轴可以找到几个不等式的解集的公共部分,从而找到不等式组的解集.
[典型例题]例1 求下列不等式组的解集:
(1) (2)
(3) (4)
解:(1)原不等式组的解集为x>7;
(2)原不等式组的解集为x≤-5;
(3)原不等式组的解集为-5<x<-2.
(4)原不等式组无解.
[归纳总结]
(三)一元一次不等式组的解法
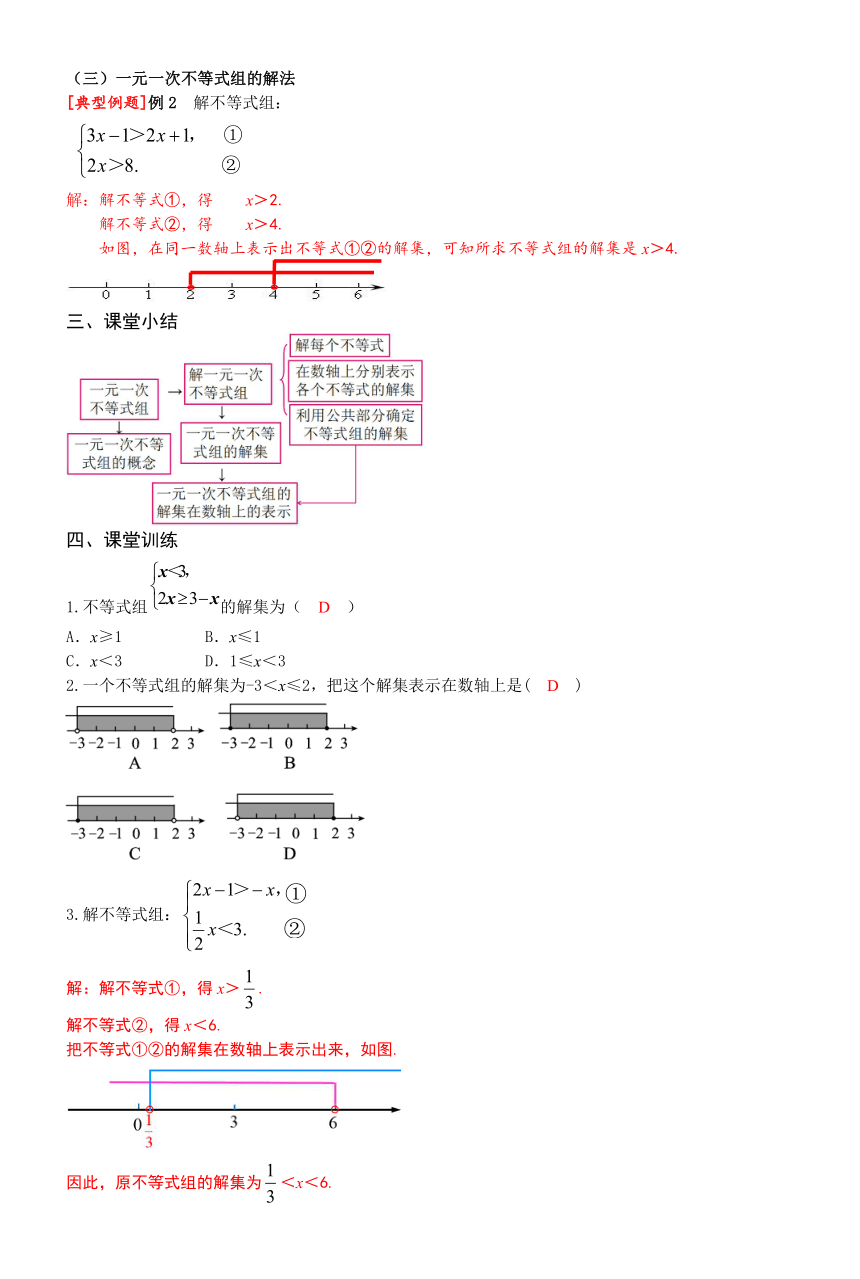
[典型例题]例2 解不等式组:
解:解不等式①,得 x>2.
解不等式②,得 x>4.
如图,在同一数轴上表示出不等式①②的解集,可知所求不等式组的解集是x>4.
三、课堂小结
四、课堂训练
1.不等式组的解集为( D )
A.x≥1 B.x≤1
C.x<3 D.1≤x<3
2.一个不等式组的解集为-3<x≤2,把这个解集表示在数轴上是( D )
3.解不等式组:
解:解不等式①,得x>.
解不等式②,得x<6.
把不等式①②的解集在数轴上表示出来,如图.
因此,原不等式组的解集为<x<6.
五、布置作业
本节课在探究对一元一次不等式组的解法上,着重讲解结合数轴观察不等式的解集,培养学生的数形结合思想,感受“形”在解题上的直观和便捷.
第2课时 一元一次不等式组及其解法(2)
1.掌握解不等式组的步骤,能熟练确定不等式组的解集.(重点)
2.会根据条件求不等式组的特殊解.(重点、难点)
一、新课导入
[复习导入]
怎么确定一元一次不等式组的解集?
(1)数轴法:在数轴上表示出各解集,找出公共部分.
(2)口诀法:同大取大,同小取小,大小小大中间找,大大小小找不到.
二、新知探究
(一)无解的一元一次不等式组
[典型例题]例1 解不等式组:
解:解不等式①,得x<-1.
解不等式②,得x≥2.
如图,在同一数轴上表示出不等式①②的解集。容易看出,这两个不等式的解集没有公共部分.因此,这个不等式组无解.
[针对训练]解不等式:
解:解不等式①,得x<-6.
解不等式②,得x>2.
把①②的解集在数轴上表示出来为:
所以不等式组无解.
一元一次不等式组的特殊解
[典型例题]例2 解不等式组:
并写出它的所有的非负整数解.
解:解不等式5x-17<8(x-1),得x>-3,
解不等式x-5≤,得x≤2,
∴不等式组的解集为-3<x≤2,
∴不等式组的非负整数解为0、1、2.
[方法总结]先求出不等式组的解集,再根据解集得出待定的整数解.
[针对训练]
不等式组的最小整数解是( B )
A.-1 B.0 C.1 D.2
2.求不等式组的所有整数解.
解:解不等式3-4x≥-1,得x≤1,
解不等式x-1≥-2(x+2),得x≥-1,
∴不等式组的解集为-1≤x≤1,
∴不等式组的所有整数解是-1、0、1.
三、课堂小结
四、课堂训练
1.不等式组的解集为( A )
A.x<-1 B.x>1
C.x<-1或x>1 D.无解
2.不等式组1<3x-7<8的所有整数解的和为 7 .
3.解不等式组:
无解
4.解不等式组把不等式组的解集在数轴上表示出来,并写出不等式组的整数解.
解:
由①,得x≥-1.
由②,得x<3.
如图,在同一数轴上表示出不等式①②的解集,可知所求不等式组的解集是-1≤x<3.
所以不等式组的整数解为-1、0、1、2.
五、布置作业
在上一节解不等式组的基础上,利用数轴解无解的一元一次不等式组,并且会求不等式组的特殊解,逐渐提高学生的解题效率.
第1课时 一元一次不等式组及其解法(1)
1.通过具体操作,在解一元一次不等式组的过程
中形成正确的解不等式组的思路与方法.(重点、难点)
2.能够将一元一次不等式组的解集在数轴上正确表示.
一、新课导入
[情境导入]
1.同学们,你能根据上图对话片段估计出这头大象的体重范围吗 请说说你的理由.
2.若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
x≥3① x<5②
二、新知探究
(一)一元一次不等式组的定义
[合作探究]
问题 某工程队用每小时可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,求将污水抽完所用时间的范围.
解:设用xh将污水抽完,则x同时满足不等式
30x>1200,① 30x<1500.②
类比方程组和不等式组
类似于方程组,把这两个含有同一个未知数的一元一次不等式合起来,组成一个一元一次不等式组,记作
[归纳总结]
把两个(或两个以上)含有相同未知数的一元一次不等式合在一起,就得到一个一元一次不等式组.
[针对练习]判断下列不等式组是否为一元一次不等式组.
解:(1)× (2)√ (3)× (4)√
(二)一元一次不等式组的解集
思考 怎样确定上面的不等式组中x的取值范围呢?
类似方程组的解,不等式组中的各不等式解集的公共部分,就是不等式组中x的取值范围.
由不等式①,解得x>40.
由不等式②,解得x<50.
把不等式①和②的解集在数轴上表示出来(如图).
从图容易看出,x取值的范围为40<x<50.
这就是说,将污水抽完所用时间多于40h而少于50h.
[归纳总结]
不等式组中几个不等式的解集的公共部分,叫做这个不等式组的解集.解不等式组就是求它的解集.
备注:利用数轴可以找到几个不等式的解集的公共部分,从而找到不等式组的解集.
[典型例题]例1 求下列不等式组的解集:
(1) (2)
(3) (4)
解:(1)原不等式组的解集为x>7;
(2)原不等式组的解集为x≤-5;
(3)原不等式组的解集为-5<x<-2.
(4)原不等式组无解.
[归纳总结]
(三)一元一次不等式组的解法
[典型例题]例2 解不等式组:
解:解不等式①,得 x>2.
解不等式②,得 x>4.
如图,在同一数轴上表示出不等式①②的解集,可知所求不等式组的解集是x>4.
三、课堂小结
四、课堂训练
1.不等式组的解集为( D )
A.x≥1 B.x≤1
C.x<3 D.1≤x<3
2.一个不等式组的解集为-3<x≤2,把这个解集表示在数轴上是( D )
3.解不等式组:
解:解不等式①,得x>.
解不等式②,得x<6.
把不等式①②的解集在数轴上表示出来,如图.
因此,原不等式组的解集为<x<6.
五、布置作业
本节课在探究对一元一次不等式组的解法上,着重讲解结合数轴观察不等式的解集,培养学生的数形结合思想,感受“形”在解题上的直观和便捷.
第2课时 一元一次不等式组及其解法(2)
1.掌握解不等式组的步骤,能熟练确定不等式组的解集.(重点)
2.会根据条件求不等式组的特殊解.(重点、难点)
一、新课导入
[复习导入]
怎么确定一元一次不等式组的解集?
(1)数轴法:在数轴上表示出各解集,找出公共部分.
(2)口诀法:同大取大,同小取小,大小小大中间找,大大小小找不到.
二、新知探究
(一)无解的一元一次不等式组
[典型例题]例1 解不等式组:
解:解不等式①,得x<-1.
解不等式②,得x≥2.
如图,在同一数轴上表示出不等式①②的解集。容易看出,这两个不等式的解集没有公共部分.因此,这个不等式组无解.
[针对训练]解不等式:
解:解不等式①,得x<-6.
解不等式②,得x>2.
把①②的解集在数轴上表示出来为:
所以不等式组无解.
一元一次不等式组的特殊解
[典型例题]例2 解不等式组:
并写出它的所有的非负整数解.
解:解不等式5x-17<8(x-1),得x>-3,
解不等式x-5≤,得x≤2,
∴不等式组的解集为-3<x≤2,
∴不等式组的非负整数解为0、1、2.
[方法总结]先求出不等式组的解集,再根据解集得出待定的整数解.
[针对训练]
不等式组的最小整数解是( B )
A.-1 B.0 C.1 D.2
2.求不等式组的所有整数解.
解:解不等式3-4x≥-1,得x≤1,
解不等式x-1≥-2(x+2),得x≥-1,
∴不等式组的解集为-1≤x≤1,
∴不等式组的所有整数解是-1、0、1.
三、课堂小结
四、课堂训练
1.不等式组的解集为( A )
A.x<-1 B.x>1
C.x<-1或x>1 D.无解
2.不等式组1<3x-7<8的所有整数解的和为 7 .
3.解不等式组:
无解
4.解不等式组把不等式组的解集在数轴上表示出来,并写出不等式组的整数解.
解:
由①,得x≥-1.
由②,得x<3.
如图,在同一数轴上表示出不等式①②的解集,可知所求不等式组的解集是-1≤x<3.
所以不等式组的整数解为-1、0、1、2.
五、布置作业
在上一节解不等式组的基础上,利用数轴解无解的一元一次不等式组,并且会求不等式组的特殊解,逐渐提高学生的解题效率.
