湖北省恩施土家族苗族自治州利川市忠路镇初中2024-2025学年八年级下学期数学第一次月考卷(含答案)
文档属性
| 名称 | 湖北省恩施土家族苗族自治州利川市忠路镇初中2024-2025学年八年级下学期数学第一次月考卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-12 21:40:30 | ||
图片预览




文档简介
2024-2025学年八年级数学下学期第一次月考卷
(考试时间:90分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版八年级下第16、17、18.1章(二次根式+勾股定理+平行四边形)。
5.难度系数:0.65。
第一部分(选择题 共36分)
一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.若有意义,则实数的取值范围是( )
A. B. C. D.
2.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形的边长为( )
A.6 B.36 C.64 D.
3.下面是一位同学做的练习题,他的得分应是( )
填空(每小题4分,共分)①的倒数是;②的绝对值是;③;④;⑤体积为的立方体的棱长为
A.4分 B.8分 C.12分 D.16分
4.图给出了四边形的部分数据,若使得四边形为平行四边形,添加的条件可以是( )
A. B. C. D.
5.张老师在黑板上出了一道计算题:,要求同学们在“○”中填入适当的运算符号,使得计算结果是有理数,“○”中可以填的符号是( )
A.×或÷ B.+或÷ C.+或× D.—或×
6.有5个边长为1的正方形,排列形式如图1,把它们分割后拼接成图2的大正方形,则下列判断错误的是( )
A. B.
C.大正方形的边长是 D.小正方形的面积是1
7.已知三角形的三边长分别为a、b、c,求其面积.
对此问题,中外数学家曾经进行过深入研究.
古希腊几何学家海伦(Heron,约公元50年),给出了求其面积的海伦公式:
,其中 ①
我国南宋时期数学家秦九韶(约1202~1261),给出了著名的秦九韶公式:
.②
若一个三角形的三边长依次为,,,请选用适当的公式求出这个三角形的面积为( )
A. B. C. D.
8.五根小木棒的长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列图形正确的是( )
A. B. C. D.
9.如图,在中,,.若点P在边上移动,则的最小值是( )
A.3.5 B.4 C.4.5 D.4.8
10.如图所示,有一块直角三角形纸片,,将斜边翻折,使点B落在直角边的延长线上的点E处,折痕为,则的长为( )
A. B. C. D.
11.已知:,,关于下列两个说法,判断正确的是( )
①若Q有意义,则;
②设,当时,.
A.只有①正确 B.只有②正确 C.①②都正确 D.①②都不正确
12.如图,,,点M是射线上一个动点,当为直角三角形时,的长为( )
A. B. C. D.或
第二部分(非选择题 共84分)
二、填空题(本大题共4小题,每小题3分,满分12分)
13.写出一个正整数n,使是最简二次根式,则n可以是 .
14.若,则的值为 .
15.在平面直角坐标系中,已知点、、,在坐标平面内找一点D,使得以A,B,C,D四点组成的四边形为平行四边形,请写出D点坐标 .
16.如图四边形中,,,,点,分别是线段,上任意一点(含端点,但不与重合),点,分别为,的中点,则长度的最大值为 .
三、解答题(本大题共8小题,满分72分.解答应写出文字说明,证明过程或演算步骤)
17.(7分)计算:
(1)
(2)
18.(8分)如图,在中,,,.
(1)试判断与是否垂直?并通过计算进行说明;
(2)若的面积为3,求的长.
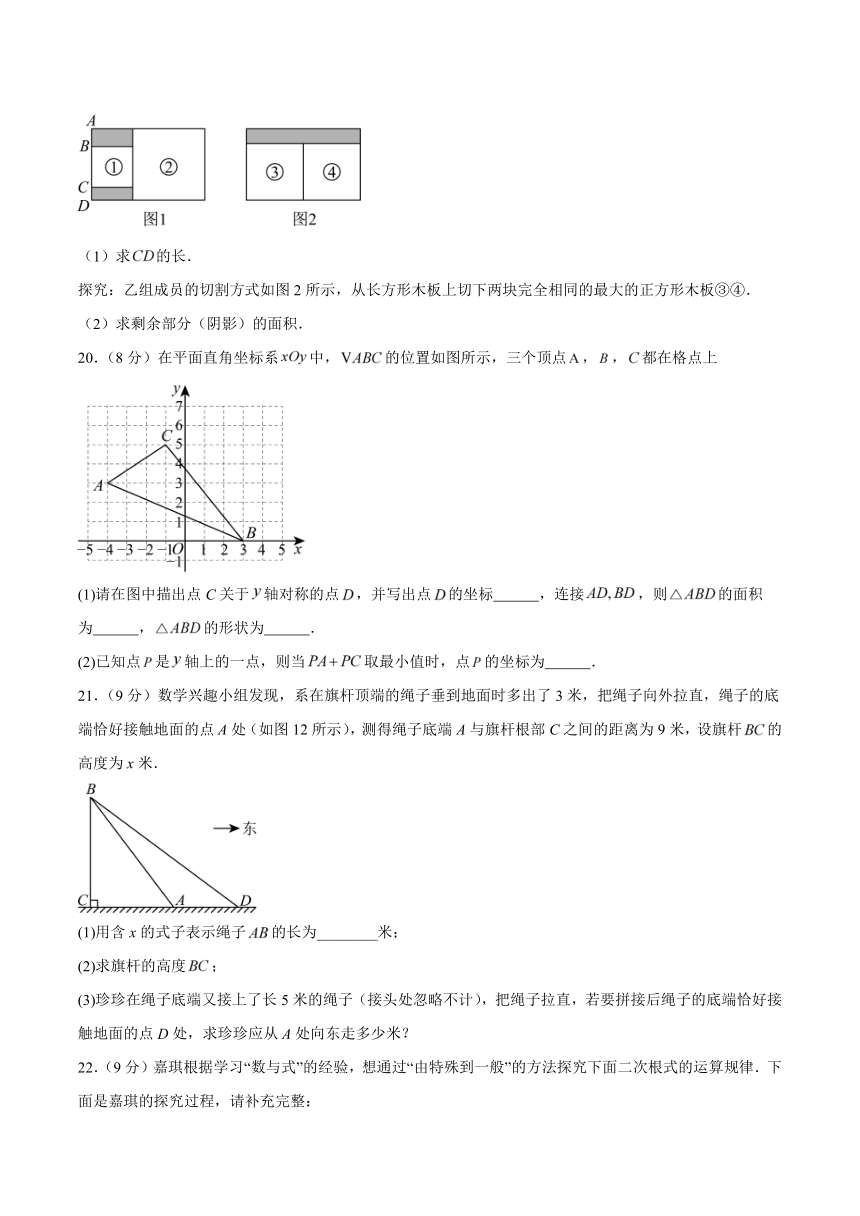
19.(8分)情景:实践小组成员利用两块相同的长方形木板各切割两个正方形木板.
操作:甲组成员的切割方式如图1所示,小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,.
(1)求的长.
探究:乙组成员的切割方式如图2所示,从长方形木板上切下两块完全相同的最大的正方形木板③④.
(2)求剩余部分(阴影)的面积.
20.(8分)在平面直角坐标系中,的位置如图所示,三个顶点,,都在格点上
(1)请在图中描出点C关于轴对称的点,并写出点的坐标 ,连接,则的面积为 ,的形状为 .
(2)已知点是轴上的一点,则当取最小值时,点的坐标为 .
21.(9分)数学兴趣小组发现,系在旗杆顶端的绳子垂到地面时多出了3米,把绳子向外拉直,绳子的底端恰好接触地面的点A处(如图12所示),测得绳子底端A与旗杆根部C之间的距离为9米,设旗杆的高度为x米.
(1)用含x的式子表示绳子的长为________米;
(2)求旗杆的高度;
(3)珍珍在绳子底端又接上了长5米的绳子(接头处忽略不计),把绳子拉直,若要拼接后绳子的底端恰好接触地面的点D处,求珍珍应从A处向东走多少米?
22.(9分)嘉琪根据学习“数与式”的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是嘉琪的探究过程,请补充完整:
(1)具体运算,发现规律:
特例1:,
特例2:,
特例3:,
特例4:______(填写一个符合上述运算特征的式子).
(2)观察、归纳,得出猜想:
如果n为正整数,用含n的式子表示上述的运算规律为:______.
(3)证明你的猜想;
(4)应用运算规律:
①化简:______;
②若(a,b均为正整数),则的值为______.
23.(11分)【模型学习】如图①,在中,,,直线l经过点C,分别过点A、B作于点D,于点E.求证:.
【模型应用】如图②,在中,,,,,直线l经过点D(不与重合).动点P从点D出发,以每秒2个单位长度的速度沿线段向点B运动,同时动点Q从点C出发,以每秒4个单位的速度沿折线向点A运动,其中一个动点到达终点时,整个运动停止.当点P、Q不与点D重合时,分别过点P、Q作于点M,于点N.设运动时间为t秒.
(1)求线段的长度;
(2)线段的长度为 ;当点Q在线段上运动时,线段的长度为 ;(用含t的代数式表示)
(3)当与全等时,求出t的值.
24.(12分)如图,在中,,,.动点从点出发沿以速度向终点运动,同时点从点出发,以速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒.
(1)的长为______.
(2)当时,用含的代数式表示线段的长______.
(3)连接.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由.
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
参考答案
一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1 2 3 4 5 6 7 8 9 10 11 12
C D C D C A B B D A A D
二、填空题(本大题共4小题,每小题3分,满分12分)
13.1(答案不唯一)
14.11
15.,,
16.
三、解答题(本大题共8小题,满分72分.解答应写出文字说明,证明过程或演算步骤)
17.(7分)
【详解】(1)解:
;·····(3分)
(2)解:
.·····(4分)
18.(8分)
【详解】(1)解:,理由如下,
,
,
是直角三角形,且,
;····(4分)
(2)解:,
,
,
.····(8分)
19.(8分)
【详解】(1)解:∵小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,
∴小正方形①的边长,小正方形②的边长,
∵,
∴,
∴的长为;···(4分)
(2)解:由(1)知大长方形的长为,宽为,
∴大长方形的面积为,
∵从长方形木板上切下两块完全相同的最大的正方形木板③④,
∴切下两块完全相同的最大的正方形边长为,
∴切下两块完全相同的最大的正方形面积为,
∴剩余部分(阴影)的面积.···(8分)
20.(8分)
【详解】(1)解:如图,点D为所作;······(1分)
由图知:,······(2分)
∵,
∴,,,
,,
,
为等腰直角三角形,······(5分)
∴;······(3分)
(2)解:如图,取格点E,F,H,根据点C与点D关于y轴对称,的最小值为的长,
·
设,网格中小正方形边长为1,
,
,即,
解得:,
,
,
,
故答案为:.······(8分)
21.(9分)
【详解】(1)解:用含x的式子表示绳子的长为米,
故答案为:;······(2分)
(2)解:由题意知:米,,
,
,
解得:,······(6分)
旗杆的高度米;
(3)解:由(2)知,米,则米,
米,
米,
珍珍应从A处向东走7米.······(9分)
22.(9分)
【详解】(1)解:根据材料提示可得,特例 4 为:,
故答案为:;······(1分)
(2)解:由上述计算可得,如果为正整数,上述的运算规律为:,
故答案为:;······(3分)
(3)解:,
等式左边等式右边;······(4分)
(4)①解:
.
②,
,
,
.······(9分)
23.(11分)
【详解】模型学习,,
,
,
,
,
,
,
;······(3分)
模型应用(1),
,
在中,由勾股定理得:,
;······(5分)
(2)动点从点出发,以每秒个单位长度的速度沿线段向点运动,
,
动点从点出发,以每秒个单位的速度沿折线向点运动,
当点在线段上运动时,线段的长度为,
故答案为:;;······(7分)
(3)当时,,
,
则,
解得;
当时,,
,
则,
解得,
综上所述:的值为或.······(11分)
24.(12分)
【详解】(1)解:∵四边形是平行四边形,
∴,
∵,
∴;·····(2分)
(2)在中,,,
由题意得,,
当点Q与点B重合时,,
∴,
当时,点Q在线段的延长线上,,
故答案为:;·····(4分)
(3)存在,理由如下:·····(5分)
如图,连接,,
若与互相平分,则四边形是平行四边形,
∴,
∴,
∴,
∴当时,与互相平分;·····(8分)
(4)当点P关于直线对称的点落在点A下方时,如图,
由对称得,,
∵,
∴,
∴,即,
∴,
∴,
∴,
解得;
当点P关于直线对称的点落在点A上方时,如图,
由对称得,,
∵,
∴,
∵
∴,
∴,
∴,
∴,
解得,
综上所述,t的值为或2.·····(12分)
试卷第2页,共28页
(考试时间:90分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版八年级下第16、17、18.1章(二次根式+勾股定理+平行四边形)。
5.难度系数:0.65。
第一部分(选择题 共36分)
一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.若有意义,则实数的取值范围是( )
A. B. C. D.
2.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形的边长为( )
A.6 B.36 C.64 D.
3.下面是一位同学做的练习题,他的得分应是( )
填空(每小题4分,共分)①的倒数是;②的绝对值是;③;④;⑤体积为的立方体的棱长为
A.4分 B.8分 C.12分 D.16分
4.图给出了四边形的部分数据,若使得四边形为平行四边形,添加的条件可以是( )
A. B. C. D.
5.张老师在黑板上出了一道计算题:,要求同学们在“○”中填入适当的运算符号,使得计算结果是有理数,“○”中可以填的符号是( )
A.×或÷ B.+或÷ C.+或× D.—或×
6.有5个边长为1的正方形,排列形式如图1,把它们分割后拼接成图2的大正方形,则下列判断错误的是( )
A. B.
C.大正方形的边长是 D.小正方形的面积是1
7.已知三角形的三边长分别为a、b、c,求其面积.
对此问题,中外数学家曾经进行过深入研究.
古希腊几何学家海伦(Heron,约公元50年),给出了求其面积的海伦公式:
,其中 ①
我国南宋时期数学家秦九韶(约1202~1261),给出了著名的秦九韶公式:
.②
若一个三角形的三边长依次为,,,请选用适当的公式求出这个三角形的面积为( )
A. B. C. D.
8.五根小木棒的长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列图形正确的是( )
A. B. C. D.
9.如图,在中,,.若点P在边上移动,则的最小值是( )
A.3.5 B.4 C.4.5 D.4.8
10.如图所示,有一块直角三角形纸片,,将斜边翻折,使点B落在直角边的延长线上的点E处,折痕为,则的长为( )
A. B. C. D.
11.已知:,,关于下列两个说法,判断正确的是( )
①若Q有意义,则;
②设,当时,.
A.只有①正确 B.只有②正确 C.①②都正确 D.①②都不正确
12.如图,,,点M是射线上一个动点,当为直角三角形时,的长为( )
A. B. C. D.或
第二部分(非选择题 共84分)
二、填空题(本大题共4小题,每小题3分,满分12分)
13.写出一个正整数n,使是最简二次根式,则n可以是 .
14.若,则的值为 .
15.在平面直角坐标系中,已知点、、,在坐标平面内找一点D,使得以A,B,C,D四点组成的四边形为平行四边形,请写出D点坐标 .
16.如图四边形中,,,,点,分别是线段,上任意一点(含端点,但不与重合),点,分别为,的中点,则长度的最大值为 .
三、解答题(本大题共8小题,满分72分.解答应写出文字说明,证明过程或演算步骤)
17.(7分)计算:
(1)
(2)
18.(8分)如图,在中,,,.
(1)试判断与是否垂直?并通过计算进行说明;
(2)若的面积为3,求的长.
19.(8分)情景:实践小组成员利用两块相同的长方形木板各切割两个正方形木板.
操作:甲组成员的切割方式如图1所示,小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,.
(1)求的长.
探究:乙组成员的切割方式如图2所示,从长方形木板上切下两块完全相同的最大的正方形木板③④.
(2)求剩余部分(阴影)的面积.
20.(8分)在平面直角坐标系中,的位置如图所示,三个顶点,,都在格点上
(1)请在图中描出点C关于轴对称的点,并写出点的坐标 ,连接,则的面积为 ,的形状为 .
(2)已知点是轴上的一点,则当取最小值时,点的坐标为 .
21.(9分)数学兴趣小组发现,系在旗杆顶端的绳子垂到地面时多出了3米,把绳子向外拉直,绳子的底端恰好接触地面的点A处(如图12所示),测得绳子底端A与旗杆根部C之间的距离为9米,设旗杆的高度为x米.
(1)用含x的式子表示绳子的长为________米;
(2)求旗杆的高度;
(3)珍珍在绳子底端又接上了长5米的绳子(接头处忽略不计),把绳子拉直,若要拼接后绳子的底端恰好接触地面的点D处,求珍珍应从A处向东走多少米?
22.(9分)嘉琪根据学习“数与式”的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是嘉琪的探究过程,请补充完整:
(1)具体运算,发现规律:
特例1:,
特例2:,
特例3:,
特例4:______(填写一个符合上述运算特征的式子).
(2)观察、归纳,得出猜想:
如果n为正整数,用含n的式子表示上述的运算规律为:______.
(3)证明你的猜想;
(4)应用运算规律:
①化简:______;
②若(a,b均为正整数),则的值为______.
23.(11分)【模型学习】如图①,在中,,,直线l经过点C,分别过点A、B作于点D,于点E.求证:.
【模型应用】如图②,在中,,,,,直线l经过点D(不与重合).动点P从点D出发,以每秒2个单位长度的速度沿线段向点B运动,同时动点Q从点C出发,以每秒4个单位的速度沿折线向点A运动,其中一个动点到达终点时,整个运动停止.当点P、Q不与点D重合时,分别过点P、Q作于点M,于点N.设运动时间为t秒.
(1)求线段的长度;
(2)线段的长度为 ;当点Q在线段上运动时,线段的长度为 ;(用含t的代数式表示)
(3)当与全等时,求出t的值.
24.(12分)如图,在中,,,.动点从点出发沿以速度向终点运动,同时点从点出发,以速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒.
(1)的长为______.
(2)当时,用含的代数式表示线段的长______.
(3)连接.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由.
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
参考答案
一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1 2 3 4 5 6 7 8 9 10 11 12
C D C D C A B B D A A D
二、填空题(本大题共4小题,每小题3分,满分12分)
13.1(答案不唯一)
14.11
15.,,
16.
三、解答题(本大题共8小题,满分72分.解答应写出文字说明,证明过程或演算步骤)
17.(7分)
【详解】(1)解:
;·····(3分)
(2)解:
.·····(4分)
18.(8分)
【详解】(1)解:,理由如下,
,
,
是直角三角形,且,
;····(4分)
(2)解:,
,
,
.····(8分)
19.(8分)
【详解】(1)解:∵小正方形①(一边与长方形边重合)的面积为,小正方形②(三边与长方形边重合)的面积为,
∴小正方形①的边长,小正方形②的边长,
∵,
∴,
∴的长为;···(4分)
(2)解:由(1)知大长方形的长为,宽为,
∴大长方形的面积为,
∵从长方形木板上切下两块完全相同的最大的正方形木板③④,
∴切下两块完全相同的最大的正方形边长为,
∴切下两块完全相同的最大的正方形面积为,
∴剩余部分(阴影)的面积.···(8分)
20.(8分)
【详解】(1)解:如图,点D为所作;······(1分)
由图知:,······(2分)
∵,
∴,,,
,,
,
为等腰直角三角形,······(5分)
∴;······(3分)
(2)解:如图,取格点E,F,H,根据点C与点D关于y轴对称,的最小值为的长,
·
设,网格中小正方形边长为1,
,
,即,
解得:,
,
,
,
故答案为:.······(8分)
21.(9分)
【详解】(1)解:用含x的式子表示绳子的长为米,
故答案为:;······(2分)
(2)解:由题意知:米,,
,
,
解得:,······(6分)
旗杆的高度米;
(3)解:由(2)知,米,则米,
米,
米,
珍珍应从A处向东走7米.······(9分)
22.(9分)
【详解】(1)解:根据材料提示可得,特例 4 为:,
故答案为:;······(1分)
(2)解:由上述计算可得,如果为正整数,上述的运算规律为:,
故答案为:;······(3分)
(3)解:,
等式左边等式右边;······(4分)
(4)①解:
.
②,
,
,
.······(9分)
23.(11分)
【详解】模型学习,,
,
,
,
,
,
,
;······(3分)
模型应用(1),
,
在中,由勾股定理得:,
;······(5分)
(2)动点从点出发,以每秒个单位长度的速度沿线段向点运动,
,
动点从点出发,以每秒个单位的速度沿折线向点运动,
当点在线段上运动时,线段的长度为,
故答案为:;;······(7分)
(3)当时,,
,
则,
解得;
当时,,
,
则,
解得,
综上所述:的值为或.······(11分)
24.(12分)
【详解】(1)解:∵四边形是平行四边形,
∴,
∵,
∴;·····(2分)
(2)在中,,,
由题意得,,
当点Q与点B重合时,,
∴,
当时,点Q在线段的延长线上,,
故答案为:;·····(4分)
(3)存在,理由如下:·····(5分)
如图,连接,,
若与互相平分,则四边形是平行四边形,
∴,
∴,
∴,
∴当时,与互相平分;·····(8分)
(4)当点P关于直线对称的点落在点A下方时,如图,
由对称得,,
∵,
∴,
∴,即,
∴,
∴,
∴,
解得;
当点P关于直线对称的点落在点A上方时,如图,
由对称得,,
∵,
∴,
∵
∴,
∴,
∴,
∴,
解得,
综上所述,t的值为或2.·····(12分)
试卷第2页,共28页
同课章节目录
