9.4 矩形、菱形、正方形(1) 同步练习 (无答案)2024-2025学年八年级下册数学苏科版
文档属性
| 名称 | 9.4 矩形、菱形、正方形(1) 同步练习 (无答案)2024-2025学年八年级下册数学苏科版 |
|
|
| 格式 | docx | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 09:18:27 | ||
图片预览

文档简介
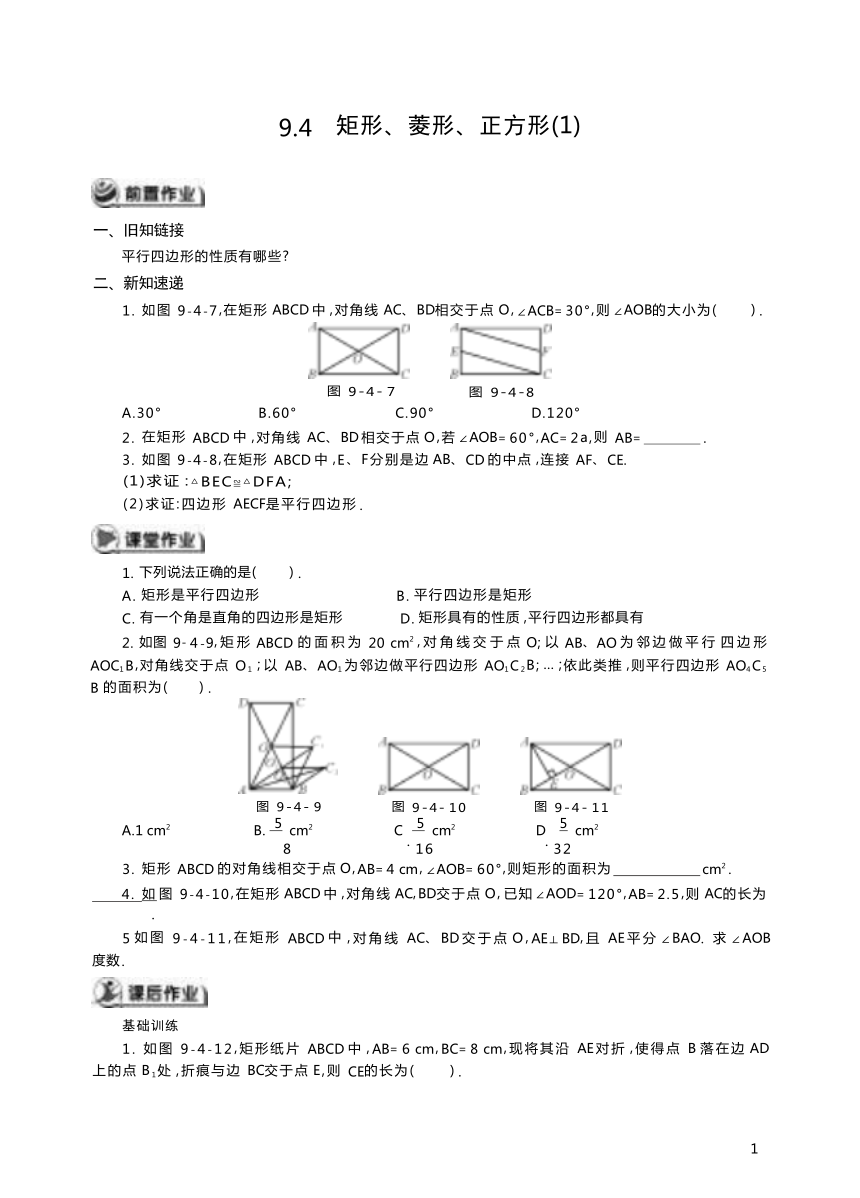
9.4 矩形、菱形、正方形(1)
一、旧知链接
平行四边形的性质有哪些
二、新知速递
1. 如图 9-4-7,在矩形 ABCD 中 ,对角线 AC、BD相交于点 O, ∠ACB= 30°,则 ∠AOB的大小为( ) .
图 9-4- 7 图 9-4-8
A.30° B.60° C.90° D.120°
2. 在矩形 ABCD 中 ,对角线 AC、BD 相交于点 O,若 ∠AOB= 60°,AC= 2a,则 AB= .
3. 如图 9-4-8,在矩形 ABCD 中 ,E、F分别是边 AB、CD 的中点 ,连接 AF、CE.
(1)求证 :△BEC≌△DFA;
(2)求证:四边形 AECF是平行四边形 .
1. 下列说法正确的是( ) .
A. 矩形是平行四边形 B. 平行四边形是矩形
C. 有一个角是直角的四边形是矩形 D. 矩形具有的性质 ,平行四边形都具有
2. 如图 9- 4 -9, 矩 形 ABCD 的 面 积 为 20 cm2 , 对 角 线 交 于 点 O; 以 AB、AO 为 邻 边 做 平 行 四 边 形 AOC1B,对角线交于点 O1 ; 以 AB、AO1 为邻边做平行四边形 AO1C2B; … ;依此类推 ,则平行四边形 AO4C5 B 的面积为( ) .
图 9-4- 9 图 9-4- 10 图 9-4- 11
A.1 cm2 B. 5 cm2 C 5 cm2 D 5 cm2
8 . 16 . 32
3. 矩形 ABCD 的对角线相交于点 O,AB= 4 cm , ∠AOB= 60°,则矩形的面积为 cm2 .
4. 如 图 9-4-10,在矩形 ABCD 中 ,对角线 AC,BD交于点 O, 已知 ∠AOD= 120°,AB= 2.5,则 AC的长为
.
5 如图 9-4-11,在矩形 ABCD 中 ,对角线 AC、BD 交于点 O,AE⊥BD,且 AE 平分 ∠BAO. 求 ∠AOB 度数 .
基础训练
1. 如图 9-4-12,矩形纸片 ABCD 中 ,AB= 6 cm ,BC= 8 cm ,现将其沿 AE 对折 ,使得点 B 落在边 AD 上的点 B1处 ,折痕与边 BC交于点 E,则 CE的长为( ) .
1
图 9-4- 12 图 9-4- 13 图 9-4- 14
A.6 cm B.4 cm C.2 cm D.1 cm
2. 如图 9-4-13,矩形 ABCD 的两条对角线相交于点 O, ∠AOD= 60°,AD= 2,则 AC的长是( ) .
A.2 B.4 C.2 3 D.4 3
3. 矩形 ABCD 的对角线 AC、BD 相交于点 O,如果 △ABC的周长比 △AOB的周长长 10厘米 ,则矩形 边 AD 的长是 厘米 .
4. 如图 9-4- 14所 示 ,E、F 是 矩 形 ABCD 对 角 线 AC 上 的 两 点 , 试 添 加 一 个 条 件 : , 使 得 △ADF≌△CBE.
5. 如图 9-4-15, 已知矩形 ABCD 中 ,E 是 AD 上的一点 ,F 是 AB 上的一点 ,EF⊥EC,且 EF= EC, DE= 4cm ,矩形 ABCD 的周长为 32 cm ,求 AE的长
图 9-4- 15 图 9-4- 16
拓展提高
6. 在矩形 ABCD 中 , 点 O 是 BC 的 中 点 , ∠AOD= 90°, 矩 形 ABCD 的 周 长 为 20 cm , 则 AB 的 长 为
( ) .
A.1 cm B.2 cm C. cm D.
7. 如图 9-4-16,在矩形 ABCD 中 ,点 E 是边 CD 的中点 ,将 △ADE 沿 AE 折叠后得到 △AFE,且点 F 在矩形 ABCD 内 部 . 将 AF延 长 交 边 BC 于 点 G. 若
则 (用含 k的代数式表示) .
8. 如图 9-4-17,在矩形 ABCD 中 ,点 E 是 BC 上一点 ,AE=AD,DF⊥AE,
垂足为 F. 求证 :DF=DC. 图 9-4-17
发散思维
9. 阅读下面短文:如 图 9- 4- 18 图(1) , △ABC 是 直 角 三 角 形 , ∠C= 90°, 现 将 △ABC 补 成 矩 形 , 使 △ABC的两个顶点为矩形一边的两个端点 ,第三个顶点落在矩形这一边的对边上 ,那么符合要求的矩形可 以画出两个矩形 ACBD 和矩形 AEFB,如图 9-4-18图(2)所示 .
(1) (2) (3) (4) 图 9-4- 18
解答问题:(1)设图(2)中矩形 ACBD 和 矩 形 AEFB 的 面 积 分 别 为 S1 、S2 , 则 S1 S2 (填 “> ”、 “= ”或“< ”) ;
(2)如图(3) ,△ABC是钝角三角形 ,按短文中的要求把它补成矩形 ,那么符合要求的矩形可以画 个 ,利用图(3)把它们画出来 ;
(3)如图(4) ,△ABC是锐角三角形且三边满足 BC>AC>AB,按短文中的要求把它补成矩形 ,那么符 合要求的矩形可以画出 个 ,利用图(4)把它们画出来 ;
(4)在(3)中所画出的矩形中 ,哪一个的周长最小 为什么
2
一、旧知链接
平行四边形的性质有哪些
二、新知速递
1. 如图 9-4-7,在矩形 ABCD 中 ,对角线 AC、BD相交于点 O, ∠ACB= 30°,则 ∠AOB的大小为( ) .
图 9-4- 7 图 9-4-8
A.30° B.60° C.90° D.120°
2. 在矩形 ABCD 中 ,对角线 AC、BD 相交于点 O,若 ∠AOB= 60°,AC= 2a,则 AB= .
3. 如图 9-4-8,在矩形 ABCD 中 ,E、F分别是边 AB、CD 的中点 ,连接 AF、CE.
(1)求证 :△BEC≌△DFA;
(2)求证:四边形 AECF是平行四边形 .
1. 下列说法正确的是( ) .
A. 矩形是平行四边形 B. 平行四边形是矩形
C. 有一个角是直角的四边形是矩形 D. 矩形具有的性质 ,平行四边形都具有
2. 如图 9- 4 -9, 矩 形 ABCD 的 面 积 为 20 cm2 , 对 角 线 交 于 点 O; 以 AB、AO 为 邻 边 做 平 行 四 边 形 AOC1B,对角线交于点 O1 ; 以 AB、AO1 为邻边做平行四边形 AO1C2B; … ;依此类推 ,则平行四边形 AO4C5 B 的面积为( ) .
图 9-4- 9 图 9-4- 10 图 9-4- 11
A.1 cm2 B. 5 cm2 C 5 cm2 D 5 cm2
8 . 16 . 32
3. 矩形 ABCD 的对角线相交于点 O,AB= 4 cm , ∠AOB= 60°,则矩形的面积为 cm2 .
4. 如 图 9-4-10,在矩形 ABCD 中 ,对角线 AC,BD交于点 O, 已知 ∠AOD= 120°,AB= 2.5,则 AC的长为
.
5 如图 9-4-11,在矩形 ABCD 中 ,对角线 AC、BD 交于点 O,AE⊥BD,且 AE 平分 ∠BAO. 求 ∠AOB 度数 .
基础训练
1. 如图 9-4-12,矩形纸片 ABCD 中 ,AB= 6 cm ,BC= 8 cm ,现将其沿 AE 对折 ,使得点 B 落在边 AD 上的点 B1处 ,折痕与边 BC交于点 E,则 CE的长为( ) .
1
图 9-4- 12 图 9-4- 13 图 9-4- 14
A.6 cm B.4 cm C.2 cm D.1 cm
2. 如图 9-4-13,矩形 ABCD 的两条对角线相交于点 O, ∠AOD= 60°,AD= 2,则 AC的长是( ) .
A.2 B.4 C.2 3 D.4 3
3. 矩形 ABCD 的对角线 AC、BD 相交于点 O,如果 △ABC的周长比 △AOB的周长长 10厘米 ,则矩形 边 AD 的长是 厘米 .
4. 如图 9-4- 14所 示 ,E、F 是 矩 形 ABCD 对 角 线 AC 上 的 两 点 , 试 添 加 一 个 条 件 : , 使 得 △ADF≌△CBE.
5. 如图 9-4-15, 已知矩形 ABCD 中 ,E 是 AD 上的一点 ,F 是 AB 上的一点 ,EF⊥EC,且 EF= EC, DE= 4cm ,矩形 ABCD 的周长为 32 cm ,求 AE的长
图 9-4- 15 图 9-4- 16
拓展提高
6. 在矩形 ABCD 中 , 点 O 是 BC 的 中 点 , ∠AOD= 90°, 矩 形 ABCD 的 周 长 为 20 cm , 则 AB 的 长 为
( ) .
A.1 cm B.2 cm C. cm D.
7. 如图 9-4-16,在矩形 ABCD 中 ,点 E 是边 CD 的中点 ,将 △ADE 沿 AE 折叠后得到 △AFE,且点 F 在矩形 ABCD 内 部 . 将 AF延 长 交 边 BC 于 点 G. 若
则 (用含 k的代数式表示) .
8. 如图 9-4-17,在矩形 ABCD 中 ,点 E 是 BC 上一点 ,AE=AD,DF⊥AE,
垂足为 F. 求证 :DF=DC. 图 9-4-17
发散思维
9. 阅读下面短文:如 图 9- 4- 18 图(1) , △ABC 是 直 角 三 角 形 , ∠C= 90°, 现 将 △ABC 补 成 矩 形 , 使 △ABC的两个顶点为矩形一边的两个端点 ,第三个顶点落在矩形这一边的对边上 ,那么符合要求的矩形可 以画出两个矩形 ACBD 和矩形 AEFB,如图 9-4-18图(2)所示 .
(1) (2) (3) (4) 图 9-4- 18
解答问题:(1)设图(2)中矩形 ACBD 和 矩 形 AEFB 的 面 积 分 别 为 S1 、S2 , 则 S1 S2 (填 “> ”、 “= ”或“< ”) ;
(2)如图(3) ,△ABC是钝角三角形 ,按短文中的要求把它补成矩形 ,那么符合要求的矩形可以画 个 ,利用图(3)把它们画出来 ;
(3)如图(4) ,△ABC是锐角三角形且三边满足 BC>AC>AB,按短文中的要求把它补成矩形 ,那么符 合要求的矩形可以画出 个 ,利用图(4)把它们画出来 ;
(4)在(3)中所画出的矩形中 ,哪一个的周长最小 为什么
2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
