11.2 反比例函数的图像与性质(2) 同步练习 (无答案))2024-2025学年八年级下册数学苏科版
文档属性
| 名称 | 11.2 反比例函数的图像与性质(2) 同步练习 (无答案))2024-2025学年八年级下册数学苏科版 | 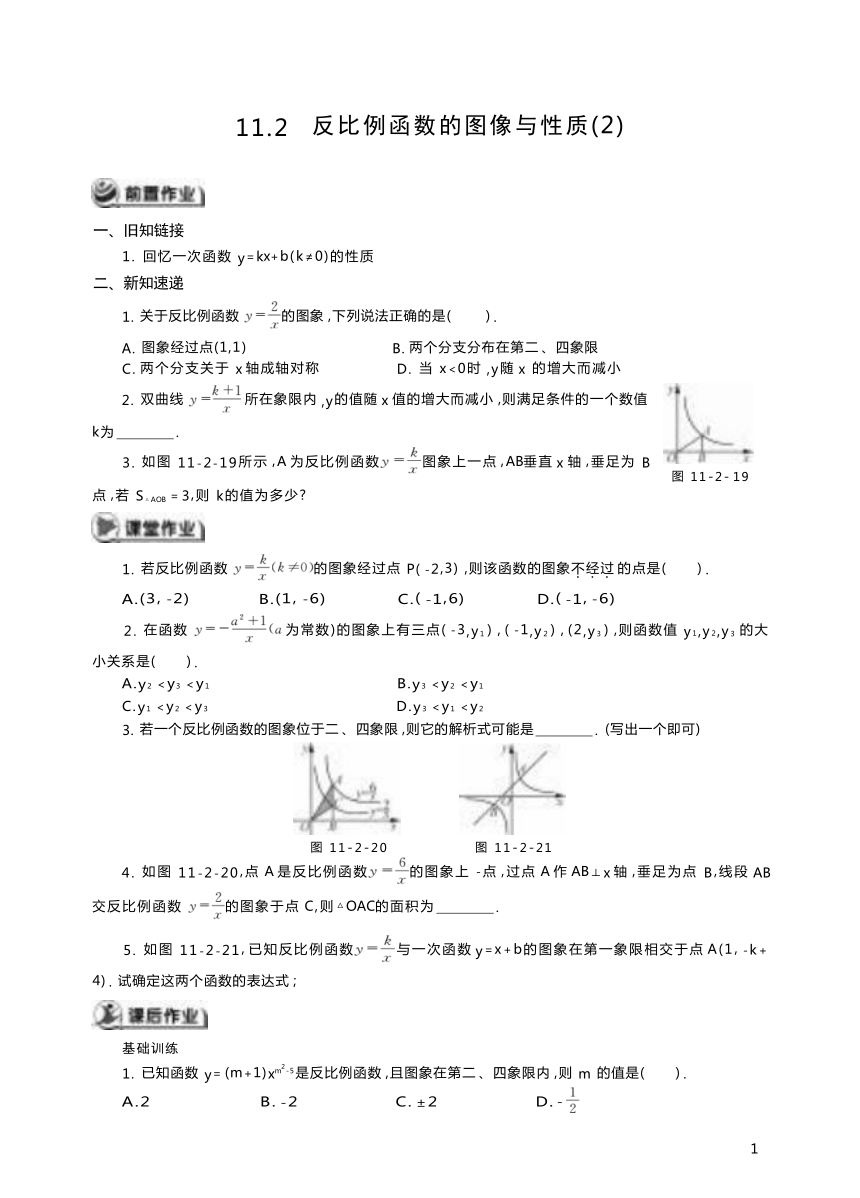 | |
| 格式 | docx | ||
| 文件大小 | 68.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 09:37:20 | ||
图片预览

文档简介
11.2 反比例函数的图像与性质(2)
1
一、旧知链接
1. 回忆一次函数 y=kx+b(k≠0)的性质
二、新知速递
1. 关于反比例函数 的图象 ,下列说法正确的是( ) .
A. 图象经过点(1,1) B. 两个分支分布在第二 、四象限
C. 两个分支关于 x 轴成轴对称 D. 当 x<0时 ,y随 x 的增大而减小
2. 双曲线 所在象限内 ,y的值随 x 值的增大而减小 ,则满足条件的一个数值
k为 .
3. 如图 11-2-19所示 ,A 为反比例函数图象上一点 ,AB垂直 x 轴 ,垂足为 B
点 ,若 S△AOB = 3,则 k的值为多少
图 11-2- 19
1. 若反比例函数 的图象经过点 P( -2,3) ,则该函数的图象不经过 的点是( ) .
A.(3, -2) B.(1, -6) C.( -1,6) D.( -1, -6)
2. 在函数 为常数)的图象上有三点( -3,y1 ) , ( -1,y2 ) , (2,y3 ) ,则函数值 y1,y2,y3 的大
小关系是( ) .
A.y2C.y1 3. 若一个反比例函数的图象位于二 、四象限 ,则它的解析式可能是 . (写出一个即可)
图 11-2-20 图 11-2-21
4. 如图 11-2-20,点 A 是反比例函数的图象上 -点 ,过点 A 作 AB ⊥x 轴 ,垂足为点 B,线段 AB 交反比例函数 的图象于点 C,则 △OAC的面积为 .
5. 如图 11-2-21, 已知反比例函数与一次函数 y=x+b的图象在第一象限相交于点 A(1, -k+
4) . 试确定这两个函数的表达式 ;
基础训练
1. 已知函数 y= (m+1)xm2-5是反比例函数 ,且图象在第二 、四象限内 ,则 m 的值是( ) .
A.2 B. -2 C. ±2 D. -
2. 平面直角坐标系中有六个点 A(1, 5) ,B -3, - ),÷ ,C( - 5, -1) ,D -2, ),÷ ,E 3, ),÷ ,F ,2),÷ ,
其中有五个点在同一反比例函数图像上 ,不在这个反比例函数图像上的点是( ) .
A. 点 C B. 点 D C. 点 E D. 点 F
3. 如图 11-2-22,三个反比例函数在 x 轴上方的图像 ,则 k1 ,k2 ,k3 的大小关系为 . (用“< ”号 连接)
图 11-2-22 图 11-2-23 图 11-2-24
4. 如图 11-2-23所示 ,一次函数 y1 =x-1与反比例函数 的图像交于点 A(2, 1) ,B( -1, -2) ,
则使 y1 >y2 的 x 的取值范围是 .
5. 如图 11-2-24,Rt△OAB中 , ∠OAB= 90°,OA=AB,且△OAB的面积为 9, 函数 y= 的图象经
过点 B.
(1)求点 B 的坐标 ;
(2)求反比例函数的解析式 . 拓展提高
6. 已知点 P 是反比例函数的图象上任一点 ,过 P 点分别作 x 轴 ,y轴的平行线 ,若两平行
线与坐标轴围成矩形的面积为 2,则 k的值为( ) .
A.2 B. -2 C. ±2 D.4
7. 下列图形中 , 阴影部分面积最大的是( ) .
A B C D
8. 在反比例函数 的图象上有两点 A(x1,y1 ) ,B(x2,y2 ) , 当 x1 <0取值范围是 .
9. 如图 11-2-25,正比例函数 的图象与反比例函数 在第
一象限的图象交于 A 点 ,过 A 点作 x 轴的垂线 ,垂足为 M, 已知 △OAM 的面积为 1.
(1)求反比例函数的解析式 ;
(2)如果 B 为反比例函数在第一象限图象上的点(点 B 与点 A 不重合) ,且 B 点 的横坐标为 1,在 x 轴上求一点 P ,使 PA + PB 最小 .
(
图
11
-
2
-
25
)发散思维
10. 已知点 A(x1,y1 ) ,B(x2,y2 ) 是 函 数 图 象 上 的 两 点 , 且 x1.
2
1
一、旧知链接
1. 回忆一次函数 y=kx+b(k≠0)的性质
二、新知速递
1. 关于反比例函数 的图象 ,下列说法正确的是( ) .
A. 图象经过点(1,1) B. 两个分支分布在第二 、四象限
C. 两个分支关于 x 轴成轴对称 D. 当 x<0时 ,y随 x 的增大而减小
2. 双曲线 所在象限内 ,y的值随 x 值的增大而减小 ,则满足条件的一个数值
k为 .
3. 如图 11-2-19所示 ,A 为反比例函数图象上一点 ,AB垂直 x 轴 ,垂足为 B
点 ,若 S△AOB = 3,则 k的值为多少
图 11-2- 19
1. 若反比例函数 的图象经过点 P( -2,3) ,则该函数的图象不经过 的点是( ) .
A.(3, -2) B.(1, -6) C.( -1,6) D.( -1, -6)
2. 在函数 为常数)的图象上有三点( -3,y1 ) , ( -1,y2 ) , (2,y3 ) ,则函数值 y1,y2,y3 的大
小关系是( ) .
A.y2
图 11-2-20 图 11-2-21
4. 如图 11-2-20,点 A 是反比例函数的图象上 -点 ,过点 A 作 AB ⊥x 轴 ,垂足为点 B,线段 AB 交反比例函数 的图象于点 C,则 △OAC的面积为 .
5. 如图 11-2-21, 已知反比例函数与一次函数 y=x+b的图象在第一象限相交于点 A(1, -k+
4) . 试确定这两个函数的表达式 ;
基础训练
1. 已知函数 y= (m+1)xm2-5是反比例函数 ,且图象在第二 、四象限内 ,则 m 的值是( ) .
A.2 B. -2 C. ±2 D. -
2. 平面直角坐标系中有六个点 A(1, 5) ,B -3, - ),÷ ,C( - 5, -1) ,D -2, ),÷ ,E 3, ),÷ ,F ,2),÷ ,
其中有五个点在同一反比例函数图像上 ,不在这个反比例函数图像上的点是( ) .
A. 点 C B. 点 D C. 点 E D. 点 F
3. 如图 11-2-22,三个反比例函数在 x 轴上方的图像 ,则 k1 ,k2 ,k3 的大小关系为 . (用“< ”号 连接)
图 11-2-22 图 11-2-23 图 11-2-24
4. 如图 11-2-23所示 ,一次函数 y1 =x-1与反比例函数 的图像交于点 A(2, 1) ,B( -1, -2) ,
则使 y1 >y2 的 x 的取值范围是 .
5. 如图 11-2-24,Rt△OAB中 , ∠OAB= 90°,OA=AB,且△OAB的面积为 9, 函数 y= 的图象经
过点 B.
(1)求点 B 的坐标 ;
(2)求反比例函数的解析式 . 拓展提高
6. 已知点 P 是反比例函数的图象上任一点 ,过 P 点分别作 x 轴 ,y轴的平行线 ,若两平行
线与坐标轴围成矩形的面积为 2,则 k的值为( ) .
A.2 B. -2 C. ±2 D.4
7. 下列图形中 , 阴影部分面积最大的是( ) .
A B C D
8. 在反比例函数 的图象上有两点 A(x1,y1 ) ,B(x2,y2 ) , 当 x1 <0
9. 如图 11-2-25,正比例函数 的图象与反比例函数 在第
一象限的图象交于 A 点 ,过 A 点作 x 轴的垂线 ,垂足为 M, 已知 △OAM 的面积为 1.
(1)求反比例函数的解析式 ;
(2)如果 B 为反比例函数在第一象限图象上的点(点 B 与点 A 不重合) ,且 B 点 的横坐标为 1,在 x 轴上求一点 P ,使 PA + PB 最小 .
(
图
11
-
2
-
25
)发散思维
10. 已知点 A(x1,y1 ) ,B(x2,y2 ) 是 函 数 图 象 上 的 两 点 , 且 x1
2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
