2025年九年级中考数学三轮冲刺练习圆中相似与锐角三角函数综合问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习圆中相似与锐角三角函数综合问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 06:41:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习圆中相似与锐角三角函数综合问题
1.如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE,OE.
(1)求证:DE是⊙O的切线(提示:利用DE是直角三角形斜边的中线进行证明);
(2)若BD=8,CD=6,DE=4,求∠EOC的正切值.
2.如图,△ABC内接于⊙O,AB为直径,作弦DE分别交AB,BC于点F,G,且点C是的中点,连结CD,BD.
(1)若∠ABC=α,则∠BCD= .(用含α的代数式表示)
(2)若AB⊥ED,当△GCD为等腰三角形时,求∠ABC的度数.
(3)若,求的值.
3.如图,已知AB为⊙O的直径,弦CD⊥AB于点E,G是上的动点,连结AD,AG,DG,CG.DG与AB交于点P,延长AG,DC相交于点F.
(1)求证:∠ADG=∠F;
(2)已知CDAB,
①若AB=10,tan∠F,求△CGF的周长;
②在点G的运动过程中,当△APG成为以AP为腰的等腰三角形时,求的值.
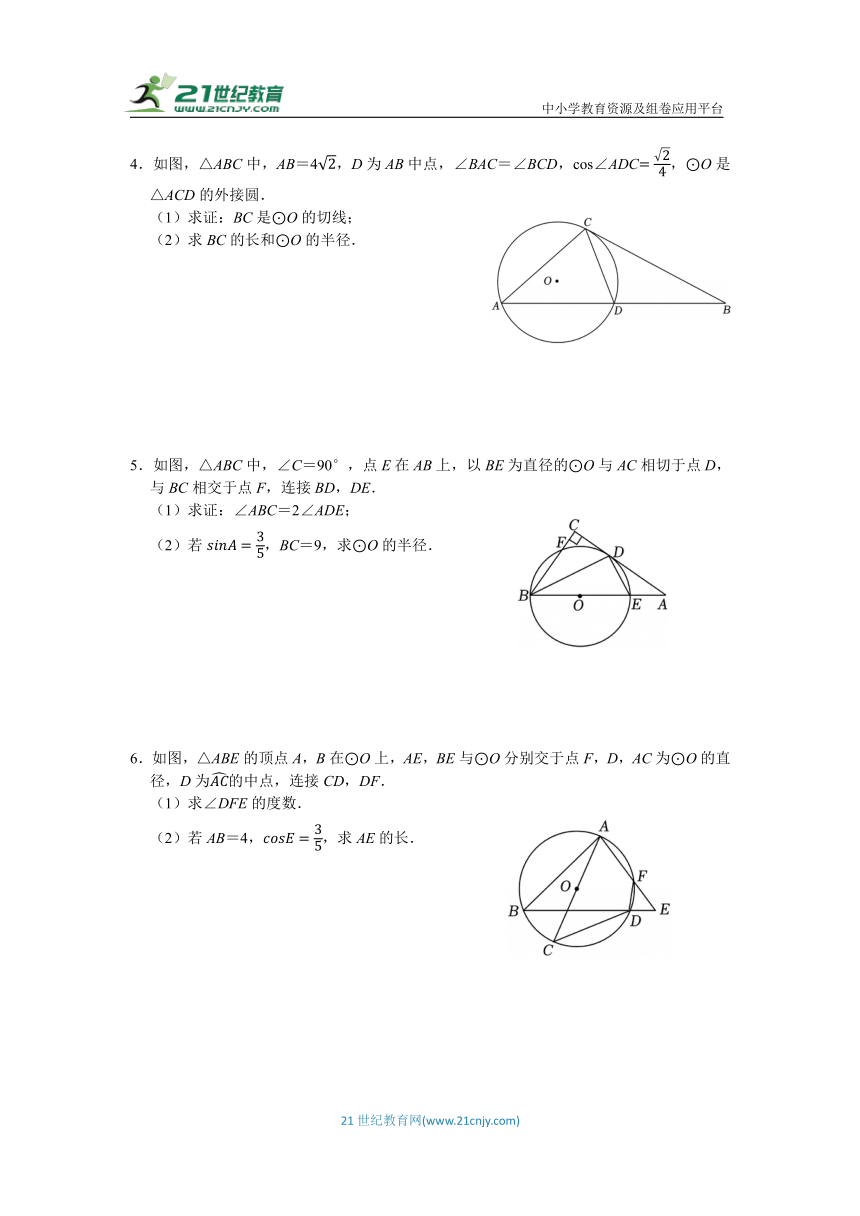
4.如图,△ABC中,AB=4,D为AB中点,∠BAC=∠BCD,cos∠ADC,⊙O是△ACD的外接圆.
(1)求证:BC是⊙O的切线;
(2)求BC的长和⊙O的半径.
5.如图,△ABC中,∠C=90°,点E在AB上,以BE为直径的⊙O与AC相切于点D,与BC相交于点F,连接BD,DE.
(1)求证:∠ABC=2∠ADE;
(2)若,BC=9,求⊙O的半径.
6.如图,△ABE的顶点A,B在⊙O上,AE,BE与⊙O分别交于点F,D,AC为⊙O的直径,D为的中点,连接CD,DF.
(1)求∠DFE的度数.
(2)若AB=4,,求AE的长.
7.如图,已知AB是⊙O的直径,直线DC是⊙O的切线,切点为C,AE⊥DC,垂足为E,连接AC.
(1)求证:AC平分∠BAE;
(2)若AC=6,,求⊙O的半径.
8.如图,在△ABC的边BC上取一点O,以O为圆心,OC为半径画⊙O与边AB相切于点D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O切线;
(2)若AB=10,,求⊙O的半径;
(3)若F是AB中点,直接写出BD、CE与AF的数量关系.
9.四边形ABCD内接于⊙O,AC为⊙O直径,连结BD,过A作AH⊥BD于点H.
(1)如图1,求证:∠BAC=∠DAH;
(2)如图2,延长AH交CD于点G,连结OD,且OD∥AB;
①求证:BD=CD;
②若cos∠BAC,AH=3,求CG的长.
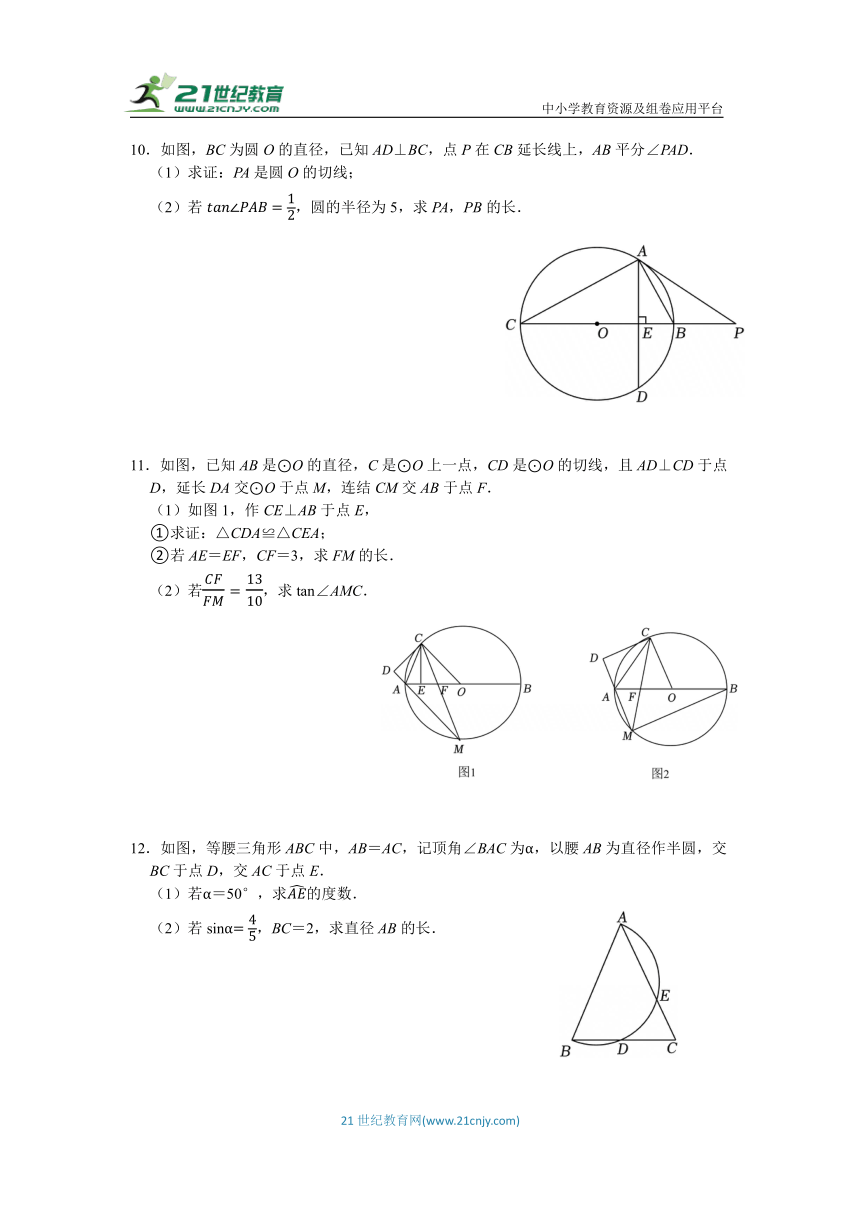
10.如图,BC为圆O的直径,已知AD⊥BC,点P在CB延长线上,AB平分∠PAD.
(1)求证:PA是圆O的切线;
(2)若,圆的半径为5,求PA,PB的长.
11.如图,已知AB是⊙O的直径,C是⊙O上一点,CD是⊙O的切线,且AD⊥CD于点D,延长DA交⊙O于点M,连结CM交AB于点F.
(1)如图1,作CE⊥AB于点E,
①求证:△CDA≌△CEA;
②若AE=EF,CF=3,求FM的长.
(2)若,求tan∠AMC.
12.如图,等腰三角形ABC中,AB=AC,记顶角∠BAC为α,以腰AB为直径作半圆,交BC于点D,交AC于点E.
(1)若α=50°,求的度数.
(2)若sinα,BC=2,求直径AB的长.
13.⊙O是等腰△ABC的外接圆,AB=AC,⊙O的直径为10,点D是弧ACB上的一点,连结BD,AD,过点A作AE⊥BD于点E.
(1)如图1,若点D在上,∠EAD=α,求∠BAC的度数(用含α的代数式表示).
(2)在(1)的条件下,若tanα,求S△ABC.
(3)若弦BD经过圆心O,连结CD,且,求DE的长.
14.如图,AB是⊙O的直径,C,D是⊙O上两点,CO平分∠BCD,过点C作CE⊥AD,垂足为E.
(1)求证:CE是⊙O的切线;
(2)已知AB=10,,求AD的长.
15.如图,在△ABC中,∠ACB=90°,AO平分∠BAC,交BC于点O.以O为圆心,OC为半径作⊙O,分别交AO,BC于点E,F.
(1)求证:AB是⊙O的切线;
(2)延长AO交⊙O于点D,连接CD,CE,若AD=6,AC=2,求tanD的值.
16.如图,四边形ABCD内接于⊙O,AB=AC,AC⊥BD于点H.
(1)求的值;
(2)求证:BH﹣HD=CD;
(3)若tan∠ABC=3,求的值.
17.如图,AB是⊙O的直径,点C在⊙O上,∠BAC的平分线交⊙O于点D,交BC于点H,过点D的直线EF∥BC,分别交AB,AC的延长线于点E,F.
(1)求证:直线EF是⊙O的切线;
(2)若,,求BC和AH的长.
18.如图,△ABC内接于⊙O,∠ACB=45°,连接OA,过B作⊙O的切线交AC的延长线于点D.
(1)求证:∠DBC=∠BAD;
(2)若,,求⊙O半径的长.
参考答案
1.【解答】(1)证明:连接OD,如图,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠ADC=90°,
∵,
∴∠EDC=∠ECD,
∵OD=OC,
∴∠ODC=∠OCD,
由题意可得:AC⊥OC,
∴∠EDC+∠ODC=∠ECD+∠OCD=90°,
∴DE⊥OD
∴DE是⊙O的切线
(2)解:∵BD=8,CD=6,
∴,
∵∠BDC=∠BCA=90°,∠B=∠B,
∴△BCD∽△BAC,
∴,
即,
∴
连接OE,则OE∥AB,
∴∠EOC=∠B,
∴.
2.【解答】解:(1)如图a所示,连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵点C是的中点,
∴∠ABC=∠DBC=α,即∠ABD=2α,
∴∠BAD=90°﹣2α,
又∵∠BAD与∠BCD所对弧为弧BD,
故∠BCD=90°﹣2α,
故答案为:90°﹣2α.
(2)当△GCD为等腰三角形时,可分为GD=CD或CG=CD或GC=GD三类情形:
设∠ABC=α,
∵AB⊥ED,
则有①当GD=CD时,∠CGD=∠BCD,如图b所示,
∴∠FGB=90°﹣α=∠CGD,
由(1)知∠BCD=90°﹣2α,
即90°﹣α=90°﹣2α,无解,故此种情形不成立;
②当CG=CD时,有∠CGD=∠CDG,如图c所示,
同理得∠CGD=90°﹣α,连接AD,
∵∠CDA=∠ABC=α,
由(1)知∠BAD=90°﹣2α,从而知∠ADE=2α,
故∠CDG=α+2α=3α,
即90°﹣α=3α,解得α=22.5°;
③当GC=GD时,有∠GCD=∠GDC,如图d所示,连接AD,
∵∠GCD=90°﹣2α,同理得∠GDC=3α,
即90°﹣2α=3α,解得α=18°,
综上,∠ABC=22.5°或18°.
(3)如图e所示,
∵tan∠BAC,设AC=2k,BC=3k,则由勾股定理有AB,
∴sin∠ABC=sin∠CBD,
∵点C是的中点,
∴AC=DC,
又∵CD=CG,
∴AC=DC=CG=2k,
∴BG=BC﹣CG=3k﹣2k=k.
延长BD至H,
从而有AC=HC.
设∠ABC=α,由(1)可得∠BCD=90°﹣2α,
∵四边形ABDC为⊙O内接四边形,
∴∠BAC+∠BDC=180°,
又∵∠BDC+∠CDH=180°,
∴∠CDH=∠BAC=90°﹣α,
∵CD=CG,
∴∠GDC45°+α,
∴∠GDB=180°﹣∠CDH﹣∠GDC=45°.
作GM⊥BD于点M,
∵sin∠CBD,
∴GMk,
∴GD.
连接EB,
∵∠BEG=∠DCG,∠EGB=∠CGD,
∴△EBG∽△CDG,
∴,
∴EG,
∴DE=EG+DG,
∴.
3.【解答】(1)证明:连接BG,如图:
∵CD⊥AB,
∴∠AEF=90°,
∴∠F+∠BAF=90°,
∵AB为⊙O的直径,
∴∠AGB=90°,
∴∠ABG+∠BAF=90°,
∴∠ABG=∠F,
∵,
∴∠ADG=∠ABG,
∴∠ADG=∠F;
(2)解:①连接BG,OD,如图:
∵AB=10,CDAB,
∴CD10=6,
∵CD⊥AB,
∴DECD6=3,
∵ODAB=5,
∴OE4,
∴AE=OA+OE=5+4=9,
∴AD2=DE2+AE2=32+92=90,
∴AD=3,
由(1)知,∠ABG=∠F,
∵tanF,
∴tan∠ABG,
∴,
设AG=3x,则BG=4x,
∵∠AGB=90°,AB=10,
∴(3x)2+(4x)2=102,
解得x=2(负值已舍去),
∴AG=3x=3×2=6,
∵∠DAG=∠FAD,∠ADG=∠F,
∴△ADG∽△AFD,
∴,即,
∴AF=15,
∴GF=AF﹣AG=15﹣6=9,
∵四边形ADCG为圆的内接四边形,
∴∠GCF=∠DAF,
∵∠F=∠F,
∴△GCF∽△DAF,
∴,
∴,
解得CG,CF=9,
∴CF+GF+CG=9+918,
∴△CGF的周长为18;
②连接OD,BD,如图:
设AB=10k,
∵CDAB,
∴CD10k=6k,
∵CD⊥AB,
∴DECD6k=3k,
∵ODAB=5k,
∴OE4k,
∴AE=OA+OE=9k,BE=OB﹣OE=k,
∴BDk,AD3k,
(Ⅰ)当AP=AG时,
∴∠AGP=∠APG=∠DPB,
∵,
∴∠AGP=∠ABD,
∴∠DPB=∠ABD,
∴PD=BDk,
∴PEk,
∴AP=AE﹣PE=9k﹣k=8k=AG,BP=BE+PE=k+k=2k,
由相交弦定理可得AP BP=PD PG,
∴PGk,
∴DG=PD+PGkkk,
∵∠GCF=∠DAG,∠F=∠ADG,
∴△GCF∽△GAD,
∴;
(Ⅱ)当AP=GP时,如图:
∵AP=GP,
∴∠PAG=∠PGA.
∵CD⊥AB,
∴,
∴∠PGA=∠ADC,
∴∠PAG=∠ADC.
∵∠ADC+∠DAE=90°,
∴∠PAG+∠DAE=90°,
∴∠DAG=90°,
∴DG为⊙O的直径,
∴DG=AB=10k,AGk,
∵∠GCF=∠DAG,∠F=∠ADG,
∴△GCF∽△GAD,
∴10;
综上所述,的值为或10.
4.【解答】(1)证明:连接OC并延长交⊙O于点M,连接MD,
则:∠M=∠A,∠CDM=90°,
∴∠M+∠MCD=90°,
∵∠BAC=∠BCD,
∴∠M=∠BCD,
∴∠BCD+∠MCD=90°,
∴∠OCB=90°,
∴OC⊥BC,
∵OC是⊙O的半径,
∴BC是⊙O的切线;
(2)解:∵∠BAC=∠BCD,∠B=∠B,
∴△BAC∽△BCD.
∴,即BC2=AB BD;
∵,D为AB中点,
∴,
∴BC2=AB BD=16,
∴BC=4.
过点A作AE⊥CD,垂足为E,连接CO,并延长交⊙O于F,连接AF,
∵在Rt△AED中,.
∵,
∴DE=1.
∴.
∵△BAC∽△BCD,
∴.
设CD=x,则,CE=CD﹣DE=x﹣1.
∵AC2=CE2+AE2,
∴,
解得x1=2,x2=﹣4(舍去).
∴CD=2,,
∵,
∴∠AFC=∠ADC,
∵CF为⊙O的直径,
∴∠CAF=90°,
∴,
∴,
∴⊙O的半径为.
5.【解答】(1)证明:连接OD,如图,
由切线性质可知:OD⊥AD,
∴∠ODA=90°,
∵BE为直径,
∴∠BDE=90°,
∴∠DBE+∠BED=90°,∠ADE+∠ODE=90°,
∵OD=OE,
∴∠ODE=∠OED,
∴∠ADE=∠DBE,
∵∠C=∠ADO=90°,
∴BC∥OD,
∴∠CBD=∠BDO,
∵OD=OB,
∴∠BDO=∠DBE,
∴∠CBD=∠DBE,即∠ABC=2∠DBE,
∴∠ABC=2∠ADE;
(2)解:设⊙O的半径为r,
在Rt△ACB中,,
∴,
由条件可知OD∥BC,
∴∠ADO=∠ACB,∠AOD=∠ABC,
∴△ADO∽△ACB,
∴,即,
解得,
即⊙O的半径为.
6.【解答】解:(1)如图,连接AD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∵D为的中点,
∴,
∴∠C=∠CAD=45°,
∵,
∴∠B=∠C=45°,
∵四边形ABDF是圆内接四边形,
∴∠B+∠AFD=180°,
∵∠AFD+∠DFE=180°,
∴∠DFE=∠B=45°;
(2)如图,过点A作AH⊥BE于点H,
由(1)知,∠B=45°,
∴△ABH为等腰直角三角形,
∵AB=4,
∴,
∵,
∴设AE=5x,则EH=3x,
∴AH2+EH2=AE2,
即,
解得(负值已舍去),
∴.
7.【解答】(1)证明:连接OC,则OC=OA,
∴∠BAC=∠OCA,
∵直线DC是⊙O的切线,切点为C,
∴DC⊥OC,
∵AE⊥DC,
∴AE∥OC,
∴∠EAC=∠OCA,
∴∠BAC=∠EAC,
∴AC平分∠BAE.
(2)解:连接BC,
∵AB是⊙O的直径,DE⊥OC于点C,
∴∠ACB=∠OCE=90°,
∴∠OCB=∠ACE=90°﹣∠OCA,
∵OC=OB,AC=6,
∴∠OCB=∠B,
∴∠B=∠ACE,
∴tanB=tan∠ACE,
∴BC=2AC=12,
∴AB6,
∴OAAB=3,
∴⊙O的半径长为3.
8.【解答】(1)证明:连OD,如图1,
在△AOC和△AOD中,
,
∴△AOC≌△AOD(SSS),
∴∠ACO=∠ADO,
∵AB与⊙O相切,
∴OD⊥AB,
∴∠ADO=90°,
∴∠ACO=90°,
∴OC⊥AC,
∵OC为半径,
∴AC是⊙O切线;
(2)解:连接OD,如图2,
∵,
∴设BC=3x,则CA=4x,
∴(4x)2+(3x)2=100,
∴x=2,
∴BC=6,
设OD=OC=a,则OB=6﹣a,
∵,
∴,
∴,
∴,
∴,
∴⊙O半径为;
(3)解:AF=BD+CE,理由如下:
连接OD,DE,如图3,
由(1)可知:△AOC≌△AOD,
∴∠ACO=∠ADO=90°,∠AOC=∠AOD,
在△COE和△DOE中,
,
∴△COE≌△DOE(SAS),
∴∠OCE=∠ODE,CE=DE,
∵OC=OE=OD,
∴∠OCE=∠OEC=∠OED=∠ODE,
∴∠DEF=180°﹣∠OEC﹣∠OED=180°﹣2∠OCE,
∵点F是AB中点,∠ACB=90°,
∴CF=BF=AF,
∴∠FCB=∠FBC,
∴∠DFE=180°﹣∠FCB﹣∠FBC=180°﹣2∠FCB=180°﹣2∠OCE,
∴∠DEF=∠DFE,
∴DE=DF=CE,
∴AF=BF=DF+BD=BD+CE.
9.【解答】(1)证明:∵AC为⊙O直径,AH⊥BD于点H,
∴∠ABC=∠AHD=90°,
∴∠BAC+∠ACB=90°,∠DAH+∠ADB=90°,
∵∠ACB=∠ADB,
∴∠BAC=∠DAH.
(2)①证明:∵OD∥AB,
∴∠AOD=∠BAC,
∵∠BAC=∠BDC,
∴∠AOD=∠BDC,
∵∠OAD=∠DBC,
∴△OAD∽△DBC,
∴∠ODA=∠DCB,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠DBC=∠DCB,
∴BD=CD.
②解:如图2,作DL⊥AC于点L,则∠OLD=∠ALD=∠ADC=90°,
∵∠ABC=∠AHD=90°,∠BAC=∠DAH,
∴cos∠AHD=cos∠BAC,
∵AH=3,
∴ADAD3=5,
∴AGAD5,
∴DG,
设OD=OA=5m,
∵∠AOD=∠BAC,
∴cos∠AOD=cos∠BAC,
∴OLOD5m=3m,
∴AL=OA﹣OL=5m﹣3m=2m,DL4m,
∴tan∠CAD2,
∴CD=2AD=2×5=10,
∴CG=CD﹣DG=10,
∴CG的长是.
10.【解答】(1)证明:连接OA,则∠AOB=2∠C,
∵BC为⊙O的直径,AD⊥BC,
∴,∠AEC=90°,
∴∠DAB=∠C,
∵AB平分∠PAD,
∴∠PAD=2∠DAB=2∠C,
∴∠PAD=∠AOB,
∴∠OAP=∠PAD+∠OAD=∠AOB+∠OAD=90°,
∵OA是⊙O的半径,且PA⊥OA,
∴PA是⊙O的切线.
(2)解:∵∠BAC=90°,∠PAB=∠DAB=∠C,
∴tanC=tan∠PAB,
∵∠PAB=∠C,∠P=∠P,
∴△PAB∽△PCA,
∴,
∴PC=2PA,PA=2PB,
∴PC=4PB,
∵⊙O的半径为5,
∴BC=2×5=10,
∴PB+10=4PB,
∴PB,
∴PA=2,
∴PA的长为,PB的长为.
11.【解答】(1)①证明:∵CD是切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠DCA+∠ACO=90°,
∵OA=OC,
∴∠OCA=∠OAC,
∵CE⊥AB,CD⊥DM,
∴∠D=∠AEC=90°,
∴∠ACE+∠OAC=90°,
∴∠ACD=∠ACE,
∵AC=AC,
∴△CDA≌△CEA(AAS);
②解:如图1中,连接OM.
∵∠D+∠DCO=180°,
∴OC∥DM,
∴∠OCM=∠DMC,
∵AE=EF,CE⊥AF,
∴CA=CF,
∴∠ACE=∠FCE,
∵DC是切线,
∴∠DCA=∠DMC.
∵∠ACD=∠ACE,
∴∠ACD=∠ACE=∠ECF=∠OCM=22.5°,
∵OC=OM,
∴∠OCM=∠OMC=∠DMC=22.5°,
∴∠AMO=45°,
∴AMOAOC,
∵OC∥AM,
∴,
∵CF=3,
∴FM=3;
(2)解:如图2中,过点O作OH⊥AM于点H.
∵CO∥DM,
∴,
设OA=OC=13k,则AM=10k,
∵AB是直径,AB=26k,
∴∠AMB=90°,
∴BM24k,
∵OH⊥AM,
∴∠AHO=∠AMB=90°,
∴OH∥BM,
∵AO=OB,
∴AH=HM=5k,
∴OHBM=12k,
∵∠D=∠DCO=∠OHD=90°,
∴四边形CDHO是矩形,
∴CO=DH=13k,CD=OH=12k,
∴DM=DH+HM=13k+5k=18k,
∴tan∠AMC.
12.【解答】解:(1)连接AD,OE,
∵以腰AB为直径作半圆,
∴AD⊥BC,
∵∠BAC为α,α=50°,
∴∠BOE=2∠BAC=2α=100°,
∴∠AOE=80°,
∴的度数为80°;
(2)∵sinα,
∴设AB=AC=5x,则BE=4x,
在Rt△ABE中,AE3x,
∴CE=AC﹣AE=2x,
在Rt△BCE中,BE2+CE2=BC2,
∴16x2+4x2=4,解得x(负值舍去),
∴AB=5x,
∴直径AB的长为.
13.【解答】解:(1)连接AO并延长,交BC于点H,如图,
∵AB=AC,
∴,
∴AH⊥BC,
∴∠BAH=∠CAHBAC.
∵∠ADB=∠ACB,∠AED=∠AHC=90°,
∴△ADE∽△ACH,
∴∠DAE=∠CAH=α,
∴∠BAC=2∠CAH=2α;
(2)连接AO并延长,交BC于点H,交⊙O于点F,连接FC,如图,
由(1)知:∠DAE=∠CAH=α,
∵tanα,
∴tan∠CAF,
∵AF为⊙O的直径,
∴∠AFC=90°,
∴tan∠CAF,
设FC=a,则AC=2a,
∵FC2+AC2=AF2,
∴a2+(2a)2=102,
∵a>0,
∴a=2,
∴AC=4,FC=2,
∵,
∴CH4,
∴BC=2CH=8,AH8,
∴S△ABC32;
(3)连接AO并延长交BC于点G,如图,
∵,
∴设AC=2k,则CD=3k,AB=AC=2k,
∵AB=AC,
∴,
∴AG⊥BC,
∴BG=GCBC.
∵弦BD经过圆心O,
∴BD为⊙O的直径,
∴∠BCD=∠BAD=90°,
∴DC⊥BC,
∴OG∥DC,
∵OB=OD,
∴OGCDk,
∵⊙O的直径为10,
∴BD=10,OA=5,BC,
∴AG=5,BG,
∵BG2+AG2=AB2,
∴,
∴k=2或k.
经检验,它们都是原方程的根,但负数不合题意,舍去,
∴k=2,
∴AB=4,
∴AD2,
∵,
∴AE4,
∴DE2.
14.【解答】(1)证明:∵CE⊥AD,
∴∠E=90°,
∵CO平分∠BCD,
∴∠OCB=∠OCD(角平分线的定义),
∵OB=OC,
∴∠B=∠BCO=∠D,
∴∠D=∠OCD,
∴OC∥DE(内错角相等,两直线平行),
∴∠OCE+∠E=180°,
∴∠OCE=∠E=90°,
∴CE⊥OC,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=10,,
∴BC,
∴,
∵∠OCE=∠BCA=90°,
∴∠ACE=∠BCO,
∵OC=OB,
∴∠B=∠BCO,
∴∠ACE=∠B,
∴△ACE∽△ABC,
∴,
∴,
∴,,
∵∠DEC=∠ACB=90°,∠B=∠CDE,
∴△ABC∽△CDE,
∴,
∴,
∴,
∴.
15.【解答】(1)证明:如图,过点O作OM⊥AB,垂足为点M,
由条件可知OC=OM,
∴OM为⊙O半径,且OM⊥AB,
∴AB是⊙O切线.
(2)解:∵DE是⊙O的直径,
∴∠DCE=90°,,
∴∠DCE=∠ACB,
∴∠DCO=∠ACE,
∴∠D=∠DCO,
∴∠ACE=∠D,且∠EAC=∠DAC,
∴△ACE∽△ADC,
∴.
∵AD=6,AC=2,
∴.
16.【解答】(1)解:如图1,
作射线AO,交BC于E,连接OB,OC,
∵OB=OC,AB=AC,
∴AE是BC的垂直平分线,
∴∠BAC=2∠BAE=∠CAE,
∴∠AEC=90°,
∴∠CAE+∠ACB=90°,
∵BD⊥AC,
∴∠BHC=90°,
∴∠CBD+∠ACB=90°,
∴∠CAE=∠CBD,
∵,
∴∠CAD=∠CBD,
∴∠CAE=∠CAD,
∴2;
(2)证明:如图2,
作射线AO,交BD于F,连接CF,连接OA,OB,
由(1)知,
∠CAF=∠CAD,AF是BC的垂直平分线,
∴BF=CF,
∵∠AHF=∠AHD=90°,
∴∠AFH=∠ADH,
∴AF=AD,
∴FH=DH,
∴CF=CD,
∴BH﹣HD=BH﹣FH=BF=CD;
(3)解:如图3,
作射线AO,交BD于F,交BC于E,连接CF,连接OA,OB,
由(1)(2)知,
AE⊥BC,∠BAE=∠CAE=∠CAD=∠CBD,AF=AD,CD=CF=BF,
∴∠BFE=∠ABC,
∴tan∠BFE=tan∠ABC,
∴,
设EF=a,则BE=3a,AE=9a,BFa,
∴AD=AF=AE﹣EF=9a﹣a=8a,CD,
∴.
故答案为:.
17.【解答】(1)证明:如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠BAC,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴AC∥OD,
∴∠ODE=∠F.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵EF∥BC,
∴∠F=∠ACB=∠ODE=90°,
即OD⊥EF,
∴直线EF是⊙O的切线;
(2)解:∵,
设⊙O的半径为r,则.
由条件可知∠ABC=∠E.
∵,
在Rt△OED中,,
即,
解得r=5,
∴,
∴,根据勾股定理,得.
∵,
∴AC=6,AF=8.
根据勾股定理,得.
∴DF=EF﹣DE=4,
根据勾股定理,得AD=4,
由平行线性质可知:,
即,
解得.
18.【解答】(1)证明:连接OB,则OB=OA,
∵BD与⊙O相切于点B,
∴BD⊥OB,
∴∠OBD=90°,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∴∠AOB=∠OBD,∠OAB=∠OBA=45°,
∴OA∥BD,
∴∠OAE=∠D,
∴∠BAD=∠OAB﹣∠OAE=45°﹣∠D,
∴∠DBC=∠ACB﹣∠D=45°﹣∠D,
∴∠DBC=∠BAD.
(2)解:设OB交AD于点E,OA=OB=4m,
∵∠AOE=∠EBD=90°,∠OAE=∠D,
∴tan∠OAE=tanD,
∴OEOA=3m,
∴AE5m,BE=OB﹣OE=4m﹣3m=m,
∴BDBEm,
∴DEm,
∴AD=AE+DE=5mmm,
∵∠DBC=∠BAD,∠D=∠D,BC=2,
∴△BCD∽△ABD,
∴,
∴AB=5BC=5×210,
∵ABOA=10,
∴OA=10,
∴⊙O半径的长为10.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习圆中相似与锐角三角函数综合问题
1.如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE,OE.
(1)求证:DE是⊙O的切线(提示:利用DE是直角三角形斜边的中线进行证明);
(2)若BD=8,CD=6,DE=4,求∠EOC的正切值.
2.如图,△ABC内接于⊙O,AB为直径,作弦DE分别交AB,BC于点F,G,且点C是的中点,连结CD,BD.
(1)若∠ABC=α,则∠BCD= .(用含α的代数式表示)
(2)若AB⊥ED,当△GCD为等腰三角形时,求∠ABC的度数.
(3)若,求的值.
3.如图,已知AB为⊙O的直径,弦CD⊥AB于点E,G是上的动点,连结AD,AG,DG,CG.DG与AB交于点P,延长AG,DC相交于点F.
(1)求证:∠ADG=∠F;
(2)已知CDAB,
①若AB=10,tan∠F,求△CGF的周长;
②在点G的运动过程中,当△APG成为以AP为腰的等腰三角形时,求的值.
4.如图,△ABC中,AB=4,D为AB中点,∠BAC=∠BCD,cos∠ADC,⊙O是△ACD的外接圆.
(1)求证:BC是⊙O的切线;
(2)求BC的长和⊙O的半径.
5.如图,△ABC中,∠C=90°,点E在AB上,以BE为直径的⊙O与AC相切于点D,与BC相交于点F,连接BD,DE.
(1)求证:∠ABC=2∠ADE;
(2)若,BC=9,求⊙O的半径.
6.如图,△ABE的顶点A,B在⊙O上,AE,BE与⊙O分别交于点F,D,AC为⊙O的直径,D为的中点,连接CD,DF.
(1)求∠DFE的度数.
(2)若AB=4,,求AE的长.
7.如图,已知AB是⊙O的直径,直线DC是⊙O的切线,切点为C,AE⊥DC,垂足为E,连接AC.
(1)求证:AC平分∠BAE;
(2)若AC=6,,求⊙O的半径.
8.如图,在△ABC的边BC上取一点O,以O为圆心,OC为半径画⊙O与边AB相切于点D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O切线;
(2)若AB=10,,求⊙O的半径;
(3)若F是AB中点,直接写出BD、CE与AF的数量关系.
9.四边形ABCD内接于⊙O,AC为⊙O直径,连结BD,过A作AH⊥BD于点H.
(1)如图1,求证:∠BAC=∠DAH;
(2)如图2,延长AH交CD于点G,连结OD,且OD∥AB;
①求证:BD=CD;
②若cos∠BAC,AH=3,求CG的长.
10.如图,BC为圆O的直径,已知AD⊥BC,点P在CB延长线上,AB平分∠PAD.
(1)求证:PA是圆O的切线;
(2)若,圆的半径为5,求PA,PB的长.
11.如图,已知AB是⊙O的直径,C是⊙O上一点,CD是⊙O的切线,且AD⊥CD于点D,延长DA交⊙O于点M,连结CM交AB于点F.
(1)如图1,作CE⊥AB于点E,
①求证:△CDA≌△CEA;
②若AE=EF,CF=3,求FM的长.
(2)若,求tan∠AMC.
12.如图,等腰三角形ABC中,AB=AC,记顶角∠BAC为α,以腰AB为直径作半圆,交BC于点D,交AC于点E.
(1)若α=50°,求的度数.
(2)若sinα,BC=2,求直径AB的长.
13.⊙O是等腰△ABC的外接圆,AB=AC,⊙O的直径为10,点D是弧ACB上的一点,连结BD,AD,过点A作AE⊥BD于点E.
(1)如图1,若点D在上,∠EAD=α,求∠BAC的度数(用含α的代数式表示).
(2)在(1)的条件下,若tanα,求S△ABC.
(3)若弦BD经过圆心O,连结CD,且,求DE的长.
14.如图,AB是⊙O的直径,C,D是⊙O上两点,CO平分∠BCD,过点C作CE⊥AD,垂足为E.
(1)求证:CE是⊙O的切线;
(2)已知AB=10,,求AD的长.
15.如图,在△ABC中,∠ACB=90°,AO平分∠BAC,交BC于点O.以O为圆心,OC为半径作⊙O,分别交AO,BC于点E,F.
(1)求证:AB是⊙O的切线;
(2)延长AO交⊙O于点D,连接CD,CE,若AD=6,AC=2,求tanD的值.
16.如图,四边形ABCD内接于⊙O,AB=AC,AC⊥BD于点H.
(1)求的值;
(2)求证:BH﹣HD=CD;
(3)若tan∠ABC=3,求的值.
17.如图,AB是⊙O的直径,点C在⊙O上,∠BAC的平分线交⊙O于点D,交BC于点H,过点D的直线EF∥BC,分别交AB,AC的延长线于点E,F.
(1)求证:直线EF是⊙O的切线;
(2)若,,求BC和AH的长.
18.如图,△ABC内接于⊙O,∠ACB=45°,连接OA,过B作⊙O的切线交AC的延长线于点D.
(1)求证:∠DBC=∠BAD;
(2)若,,求⊙O半径的长.
参考答案
1.【解答】(1)证明:连接OD,如图,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠ADC=90°,
∵,
∴∠EDC=∠ECD,
∵OD=OC,
∴∠ODC=∠OCD,
由题意可得:AC⊥OC,
∴∠EDC+∠ODC=∠ECD+∠OCD=90°,
∴DE⊥OD
∴DE是⊙O的切线
(2)解:∵BD=8,CD=6,
∴,
∵∠BDC=∠BCA=90°,∠B=∠B,
∴△BCD∽△BAC,
∴,
即,
∴
连接OE,则OE∥AB,
∴∠EOC=∠B,
∴.
2.【解答】解:(1)如图a所示,连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵点C是的中点,
∴∠ABC=∠DBC=α,即∠ABD=2α,
∴∠BAD=90°﹣2α,
又∵∠BAD与∠BCD所对弧为弧BD,
故∠BCD=90°﹣2α,
故答案为:90°﹣2α.
(2)当△GCD为等腰三角形时,可分为GD=CD或CG=CD或GC=GD三类情形:
设∠ABC=α,
∵AB⊥ED,
则有①当GD=CD时,∠CGD=∠BCD,如图b所示,
∴∠FGB=90°﹣α=∠CGD,
由(1)知∠BCD=90°﹣2α,
即90°﹣α=90°﹣2α,无解,故此种情形不成立;
②当CG=CD时,有∠CGD=∠CDG,如图c所示,
同理得∠CGD=90°﹣α,连接AD,
∵∠CDA=∠ABC=α,
由(1)知∠BAD=90°﹣2α,从而知∠ADE=2α,
故∠CDG=α+2α=3α,
即90°﹣α=3α,解得α=22.5°;
③当GC=GD时,有∠GCD=∠GDC,如图d所示,连接AD,
∵∠GCD=90°﹣2α,同理得∠GDC=3α,
即90°﹣2α=3α,解得α=18°,
综上,∠ABC=22.5°或18°.
(3)如图e所示,
∵tan∠BAC,设AC=2k,BC=3k,则由勾股定理有AB,
∴sin∠ABC=sin∠CBD,
∵点C是的中点,
∴AC=DC,
又∵CD=CG,
∴AC=DC=CG=2k,
∴BG=BC﹣CG=3k﹣2k=k.
延长BD至H,
从而有AC=HC.
设∠ABC=α,由(1)可得∠BCD=90°﹣2α,
∵四边形ABDC为⊙O内接四边形,
∴∠BAC+∠BDC=180°,
又∵∠BDC+∠CDH=180°,
∴∠CDH=∠BAC=90°﹣α,
∵CD=CG,
∴∠GDC45°+α,
∴∠GDB=180°﹣∠CDH﹣∠GDC=45°.
作GM⊥BD于点M,
∵sin∠CBD,
∴GMk,
∴GD.
连接EB,
∵∠BEG=∠DCG,∠EGB=∠CGD,
∴△EBG∽△CDG,
∴,
∴EG,
∴DE=EG+DG,
∴.
3.【解答】(1)证明:连接BG,如图:
∵CD⊥AB,
∴∠AEF=90°,
∴∠F+∠BAF=90°,
∵AB为⊙O的直径,
∴∠AGB=90°,
∴∠ABG+∠BAF=90°,
∴∠ABG=∠F,
∵,
∴∠ADG=∠ABG,
∴∠ADG=∠F;
(2)解:①连接BG,OD,如图:
∵AB=10,CDAB,
∴CD10=6,
∵CD⊥AB,
∴DECD6=3,
∵ODAB=5,
∴OE4,
∴AE=OA+OE=5+4=9,
∴AD2=DE2+AE2=32+92=90,
∴AD=3,
由(1)知,∠ABG=∠F,
∵tanF,
∴tan∠ABG,
∴,
设AG=3x,则BG=4x,
∵∠AGB=90°,AB=10,
∴(3x)2+(4x)2=102,
解得x=2(负值已舍去),
∴AG=3x=3×2=6,
∵∠DAG=∠FAD,∠ADG=∠F,
∴△ADG∽△AFD,
∴,即,
∴AF=15,
∴GF=AF﹣AG=15﹣6=9,
∵四边形ADCG为圆的内接四边形,
∴∠GCF=∠DAF,
∵∠F=∠F,
∴△GCF∽△DAF,
∴,
∴,
解得CG,CF=9,
∴CF+GF+CG=9+918,
∴△CGF的周长为18;
②连接OD,BD,如图:
设AB=10k,
∵CDAB,
∴CD10k=6k,
∵CD⊥AB,
∴DECD6k=3k,
∵ODAB=5k,
∴OE4k,
∴AE=OA+OE=9k,BE=OB﹣OE=k,
∴BDk,AD3k,
(Ⅰ)当AP=AG时,
∴∠AGP=∠APG=∠DPB,
∵,
∴∠AGP=∠ABD,
∴∠DPB=∠ABD,
∴PD=BDk,
∴PEk,
∴AP=AE﹣PE=9k﹣k=8k=AG,BP=BE+PE=k+k=2k,
由相交弦定理可得AP BP=PD PG,
∴PGk,
∴DG=PD+PGkkk,
∵∠GCF=∠DAG,∠F=∠ADG,
∴△GCF∽△GAD,
∴;
(Ⅱ)当AP=GP时,如图:
∵AP=GP,
∴∠PAG=∠PGA.
∵CD⊥AB,
∴,
∴∠PGA=∠ADC,
∴∠PAG=∠ADC.
∵∠ADC+∠DAE=90°,
∴∠PAG+∠DAE=90°,
∴∠DAG=90°,
∴DG为⊙O的直径,
∴DG=AB=10k,AGk,
∵∠GCF=∠DAG,∠F=∠ADG,
∴△GCF∽△GAD,
∴10;
综上所述,的值为或10.
4.【解答】(1)证明:连接OC并延长交⊙O于点M,连接MD,
则:∠M=∠A,∠CDM=90°,
∴∠M+∠MCD=90°,
∵∠BAC=∠BCD,
∴∠M=∠BCD,
∴∠BCD+∠MCD=90°,
∴∠OCB=90°,
∴OC⊥BC,
∵OC是⊙O的半径,
∴BC是⊙O的切线;
(2)解:∵∠BAC=∠BCD,∠B=∠B,
∴△BAC∽△BCD.
∴,即BC2=AB BD;
∵,D为AB中点,
∴,
∴BC2=AB BD=16,
∴BC=4.
过点A作AE⊥CD,垂足为E,连接CO,并延长交⊙O于F,连接AF,
∵在Rt△AED中,.
∵,
∴DE=1.
∴.
∵△BAC∽△BCD,
∴.
设CD=x,则,CE=CD﹣DE=x﹣1.
∵AC2=CE2+AE2,
∴,
解得x1=2,x2=﹣4(舍去).
∴CD=2,,
∵,
∴∠AFC=∠ADC,
∵CF为⊙O的直径,
∴∠CAF=90°,
∴,
∴,
∴⊙O的半径为.
5.【解答】(1)证明:连接OD,如图,
由切线性质可知:OD⊥AD,
∴∠ODA=90°,
∵BE为直径,
∴∠BDE=90°,
∴∠DBE+∠BED=90°,∠ADE+∠ODE=90°,
∵OD=OE,
∴∠ODE=∠OED,
∴∠ADE=∠DBE,
∵∠C=∠ADO=90°,
∴BC∥OD,
∴∠CBD=∠BDO,
∵OD=OB,
∴∠BDO=∠DBE,
∴∠CBD=∠DBE,即∠ABC=2∠DBE,
∴∠ABC=2∠ADE;
(2)解:设⊙O的半径为r,
在Rt△ACB中,,
∴,
由条件可知OD∥BC,
∴∠ADO=∠ACB,∠AOD=∠ABC,
∴△ADO∽△ACB,
∴,即,
解得,
即⊙O的半径为.
6.【解答】解:(1)如图,连接AD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∵D为的中点,
∴,
∴∠C=∠CAD=45°,
∵,
∴∠B=∠C=45°,
∵四边形ABDF是圆内接四边形,
∴∠B+∠AFD=180°,
∵∠AFD+∠DFE=180°,
∴∠DFE=∠B=45°;
(2)如图,过点A作AH⊥BE于点H,
由(1)知,∠B=45°,
∴△ABH为等腰直角三角形,
∵AB=4,
∴,
∵,
∴设AE=5x,则EH=3x,
∴AH2+EH2=AE2,
即,
解得(负值已舍去),
∴.
7.【解答】(1)证明:连接OC,则OC=OA,
∴∠BAC=∠OCA,
∵直线DC是⊙O的切线,切点为C,
∴DC⊥OC,
∵AE⊥DC,
∴AE∥OC,
∴∠EAC=∠OCA,
∴∠BAC=∠EAC,
∴AC平分∠BAE.
(2)解:连接BC,
∵AB是⊙O的直径,DE⊥OC于点C,
∴∠ACB=∠OCE=90°,
∴∠OCB=∠ACE=90°﹣∠OCA,
∵OC=OB,AC=6,
∴∠OCB=∠B,
∴∠B=∠ACE,
∴tanB=tan∠ACE,
∴BC=2AC=12,
∴AB6,
∴OAAB=3,
∴⊙O的半径长为3.
8.【解答】(1)证明:连OD,如图1,
在△AOC和△AOD中,
,
∴△AOC≌△AOD(SSS),
∴∠ACO=∠ADO,
∵AB与⊙O相切,
∴OD⊥AB,
∴∠ADO=90°,
∴∠ACO=90°,
∴OC⊥AC,
∵OC为半径,
∴AC是⊙O切线;
(2)解:连接OD,如图2,
∵,
∴设BC=3x,则CA=4x,
∴(4x)2+(3x)2=100,
∴x=2,
∴BC=6,
设OD=OC=a,则OB=6﹣a,
∵,
∴,
∴,
∴,
∴,
∴⊙O半径为;
(3)解:AF=BD+CE,理由如下:
连接OD,DE,如图3,
由(1)可知:△AOC≌△AOD,
∴∠ACO=∠ADO=90°,∠AOC=∠AOD,
在△COE和△DOE中,
,
∴△COE≌△DOE(SAS),
∴∠OCE=∠ODE,CE=DE,
∵OC=OE=OD,
∴∠OCE=∠OEC=∠OED=∠ODE,
∴∠DEF=180°﹣∠OEC﹣∠OED=180°﹣2∠OCE,
∵点F是AB中点,∠ACB=90°,
∴CF=BF=AF,
∴∠FCB=∠FBC,
∴∠DFE=180°﹣∠FCB﹣∠FBC=180°﹣2∠FCB=180°﹣2∠OCE,
∴∠DEF=∠DFE,
∴DE=DF=CE,
∴AF=BF=DF+BD=BD+CE.
9.【解答】(1)证明:∵AC为⊙O直径,AH⊥BD于点H,
∴∠ABC=∠AHD=90°,
∴∠BAC+∠ACB=90°,∠DAH+∠ADB=90°,
∵∠ACB=∠ADB,
∴∠BAC=∠DAH.
(2)①证明:∵OD∥AB,
∴∠AOD=∠BAC,
∵∠BAC=∠BDC,
∴∠AOD=∠BDC,
∵∠OAD=∠DBC,
∴△OAD∽△DBC,
∴∠ODA=∠DCB,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠DBC=∠DCB,
∴BD=CD.
②解:如图2,作DL⊥AC于点L,则∠OLD=∠ALD=∠ADC=90°,
∵∠ABC=∠AHD=90°,∠BAC=∠DAH,
∴cos∠AHD=cos∠BAC,
∵AH=3,
∴ADAD3=5,
∴AGAD5,
∴DG,
设OD=OA=5m,
∵∠AOD=∠BAC,
∴cos∠AOD=cos∠BAC,
∴OLOD5m=3m,
∴AL=OA﹣OL=5m﹣3m=2m,DL4m,
∴tan∠CAD2,
∴CD=2AD=2×5=10,
∴CG=CD﹣DG=10,
∴CG的长是.
10.【解答】(1)证明:连接OA,则∠AOB=2∠C,
∵BC为⊙O的直径,AD⊥BC,
∴,∠AEC=90°,
∴∠DAB=∠C,
∵AB平分∠PAD,
∴∠PAD=2∠DAB=2∠C,
∴∠PAD=∠AOB,
∴∠OAP=∠PAD+∠OAD=∠AOB+∠OAD=90°,
∵OA是⊙O的半径,且PA⊥OA,
∴PA是⊙O的切线.
(2)解:∵∠BAC=90°,∠PAB=∠DAB=∠C,
∴tanC=tan∠PAB,
∵∠PAB=∠C,∠P=∠P,
∴△PAB∽△PCA,
∴,
∴PC=2PA,PA=2PB,
∴PC=4PB,
∵⊙O的半径为5,
∴BC=2×5=10,
∴PB+10=4PB,
∴PB,
∴PA=2,
∴PA的长为,PB的长为.
11.【解答】(1)①证明:∵CD是切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠DCA+∠ACO=90°,
∵OA=OC,
∴∠OCA=∠OAC,
∵CE⊥AB,CD⊥DM,
∴∠D=∠AEC=90°,
∴∠ACE+∠OAC=90°,
∴∠ACD=∠ACE,
∵AC=AC,
∴△CDA≌△CEA(AAS);
②解:如图1中,连接OM.
∵∠D+∠DCO=180°,
∴OC∥DM,
∴∠OCM=∠DMC,
∵AE=EF,CE⊥AF,
∴CA=CF,
∴∠ACE=∠FCE,
∵DC是切线,
∴∠DCA=∠DMC.
∵∠ACD=∠ACE,
∴∠ACD=∠ACE=∠ECF=∠OCM=22.5°,
∵OC=OM,
∴∠OCM=∠OMC=∠DMC=22.5°,
∴∠AMO=45°,
∴AMOAOC,
∵OC∥AM,
∴,
∵CF=3,
∴FM=3;
(2)解:如图2中,过点O作OH⊥AM于点H.
∵CO∥DM,
∴,
设OA=OC=13k,则AM=10k,
∵AB是直径,AB=26k,
∴∠AMB=90°,
∴BM24k,
∵OH⊥AM,
∴∠AHO=∠AMB=90°,
∴OH∥BM,
∵AO=OB,
∴AH=HM=5k,
∴OHBM=12k,
∵∠D=∠DCO=∠OHD=90°,
∴四边形CDHO是矩形,
∴CO=DH=13k,CD=OH=12k,
∴DM=DH+HM=13k+5k=18k,
∴tan∠AMC.
12.【解答】解:(1)连接AD,OE,
∵以腰AB为直径作半圆,
∴AD⊥BC,
∵∠BAC为α,α=50°,
∴∠BOE=2∠BAC=2α=100°,
∴∠AOE=80°,
∴的度数为80°;
(2)∵sinα,
∴设AB=AC=5x,则BE=4x,
在Rt△ABE中,AE3x,
∴CE=AC﹣AE=2x,
在Rt△BCE中,BE2+CE2=BC2,
∴16x2+4x2=4,解得x(负值舍去),
∴AB=5x,
∴直径AB的长为.
13.【解答】解:(1)连接AO并延长,交BC于点H,如图,
∵AB=AC,
∴,
∴AH⊥BC,
∴∠BAH=∠CAHBAC.
∵∠ADB=∠ACB,∠AED=∠AHC=90°,
∴△ADE∽△ACH,
∴∠DAE=∠CAH=α,
∴∠BAC=2∠CAH=2α;
(2)连接AO并延长,交BC于点H,交⊙O于点F,连接FC,如图,
由(1)知:∠DAE=∠CAH=α,
∵tanα,
∴tan∠CAF,
∵AF为⊙O的直径,
∴∠AFC=90°,
∴tan∠CAF,
设FC=a,则AC=2a,
∵FC2+AC2=AF2,
∴a2+(2a)2=102,
∵a>0,
∴a=2,
∴AC=4,FC=2,
∵,
∴CH4,
∴BC=2CH=8,AH8,
∴S△ABC32;
(3)连接AO并延长交BC于点G,如图,
∵,
∴设AC=2k,则CD=3k,AB=AC=2k,
∵AB=AC,
∴,
∴AG⊥BC,
∴BG=GCBC.
∵弦BD经过圆心O,
∴BD为⊙O的直径,
∴∠BCD=∠BAD=90°,
∴DC⊥BC,
∴OG∥DC,
∵OB=OD,
∴OGCDk,
∵⊙O的直径为10,
∴BD=10,OA=5,BC,
∴AG=5,BG,
∵BG2+AG2=AB2,
∴,
∴k=2或k.
经检验,它们都是原方程的根,但负数不合题意,舍去,
∴k=2,
∴AB=4,
∴AD2,
∵,
∴AE4,
∴DE2.
14.【解答】(1)证明:∵CE⊥AD,
∴∠E=90°,
∵CO平分∠BCD,
∴∠OCB=∠OCD(角平分线的定义),
∵OB=OC,
∴∠B=∠BCO=∠D,
∴∠D=∠OCD,
∴OC∥DE(内错角相等,两直线平行),
∴∠OCE+∠E=180°,
∴∠OCE=∠E=90°,
∴CE⊥OC,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=10,,
∴BC,
∴,
∵∠OCE=∠BCA=90°,
∴∠ACE=∠BCO,
∵OC=OB,
∴∠B=∠BCO,
∴∠ACE=∠B,
∴△ACE∽△ABC,
∴,
∴,
∴,,
∵∠DEC=∠ACB=90°,∠B=∠CDE,
∴△ABC∽△CDE,
∴,
∴,
∴,
∴.
15.【解答】(1)证明:如图,过点O作OM⊥AB,垂足为点M,
由条件可知OC=OM,
∴OM为⊙O半径,且OM⊥AB,
∴AB是⊙O切线.
(2)解:∵DE是⊙O的直径,
∴∠DCE=90°,,
∴∠DCE=∠ACB,
∴∠DCO=∠ACE,
∴∠D=∠DCO,
∴∠ACE=∠D,且∠EAC=∠DAC,
∴△ACE∽△ADC,
∴.
∵AD=6,AC=2,
∴.
16.【解答】(1)解:如图1,
作射线AO,交BC于E,连接OB,OC,
∵OB=OC,AB=AC,
∴AE是BC的垂直平分线,
∴∠BAC=2∠BAE=∠CAE,
∴∠AEC=90°,
∴∠CAE+∠ACB=90°,
∵BD⊥AC,
∴∠BHC=90°,
∴∠CBD+∠ACB=90°,
∴∠CAE=∠CBD,
∵,
∴∠CAD=∠CBD,
∴∠CAE=∠CAD,
∴2;
(2)证明:如图2,
作射线AO,交BD于F,连接CF,连接OA,OB,
由(1)知,
∠CAF=∠CAD,AF是BC的垂直平分线,
∴BF=CF,
∵∠AHF=∠AHD=90°,
∴∠AFH=∠ADH,
∴AF=AD,
∴FH=DH,
∴CF=CD,
∴BH﹣HD=BH﹣FH=BF=CD;
(3)解:如图3,
作射线AO,交BD于F,交BC于E,连接CF,连接OA,OB,
由(1)(2)知,
AE⊥BC,∠BAE=∠CAE=∠CAD=∠CBD,AF=AD,CD=CF=BF,
∴∠BFE=∠ABC,
∴tan∠BFE=tan∠ABC,
∴,
设EF=a,则BE=3a,AE=9a,BFa,
∴AD=AF=AE﹣EF=9a﹣a=8a,CD,
∴.
故答案为:.
17.【解答】(1)证明:如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠BAC,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴AC∥OD,
∴∠ODE=∠F.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵EF∥BC,
∴∠F=∠ACB=∠ODE=90°,
即OD⊥EF,
∴直线EF是⊙O的切线;
(2)解:∵,
设⊙O的半径为r,则.
由条件可知∠ABC=∠E.
∵,
在Rt△OED中,,
即,
解得r=5,
∴,
∴,根据勾股定理,得.
∵,
∴AC=6,AF=8.
根据勾股定理,得.
∴DF=EF﹣DE=4,
根据勾股定理,得AD=4,
由平行线性质可知:,
即,
解得.
18.【解答】(1)证明:连接OB,则OB=OA,
∵BD与⊙O相切于点B,
∴BD⊥OB,
∴∠OBD=90°,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∴∠AOB=∠OBD,∠OAB=∠OBA=45°,
∴OA∥BD,
∴∠OAE=∠D,
∴∠BAD=∠OAB﹣∠OAE=45°﹣∠D,
∴∠DBC=∠ACB﹣∠D=45°﹣∠D,
∴∠DBC=∠BAD.
(2)解:设OB交AD于点E,OA=OB=4m,
∵∠AOE=∠EBD=90°,∠OAE=∠D,
∴tan∠OAE=tanD,
∴OEOA=3m,
∴AE5m,BE=OB﹣OE=4m﹣3m=m,
∴BDBEm,
∴DEm,
∴AD=AE+DE=5mmm,
∵∠DBC=∠BAD,∠D=∠D,BC=2,
∴△BCD∽△ABD,
∴,
∴AB=5BC=5×210,
∵ABOA=10,
∴OA=10,
∴⊙O半径的长为10.
21世纪教育网(www.21cnjy.com)
同课章节目录
