2025年九年级中考数学三轮冲刺练习图形的相似综合问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习图形的相似综合问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 06:40:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习图形的相似综合问题
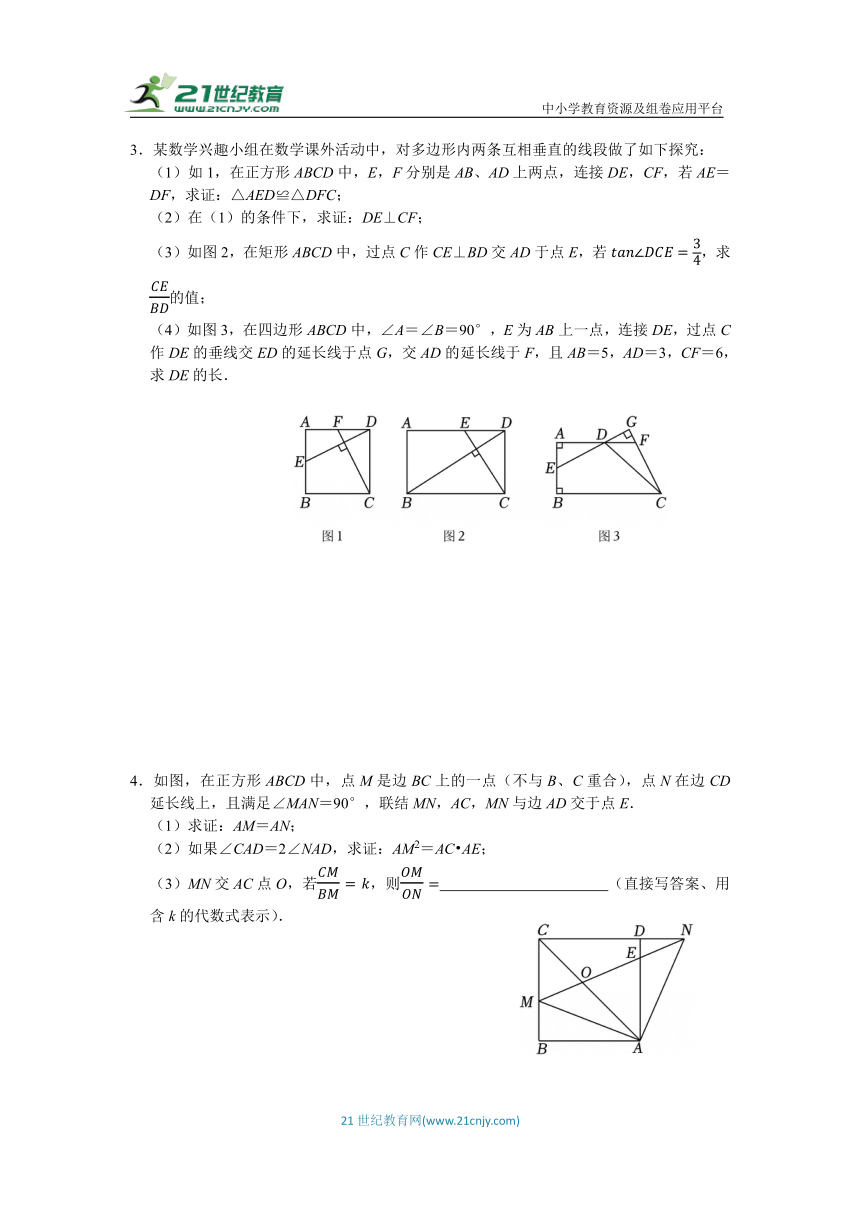
1.在Rt△ABC中,∠ACB=90°,点M为AB的中点,点F是线段CM上一动点,过点F作DE⊥CM分别交边CA,CB于点D,E.
(1)如图1,求证△CDE∽△CBA;
(2)如图1,若DE=CM,求证:BC=2DC;
(3)如图2,若点F为CM的中点,求的值.
2.如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=4,AD=6,,求AE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,,直接写出的值.
3.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
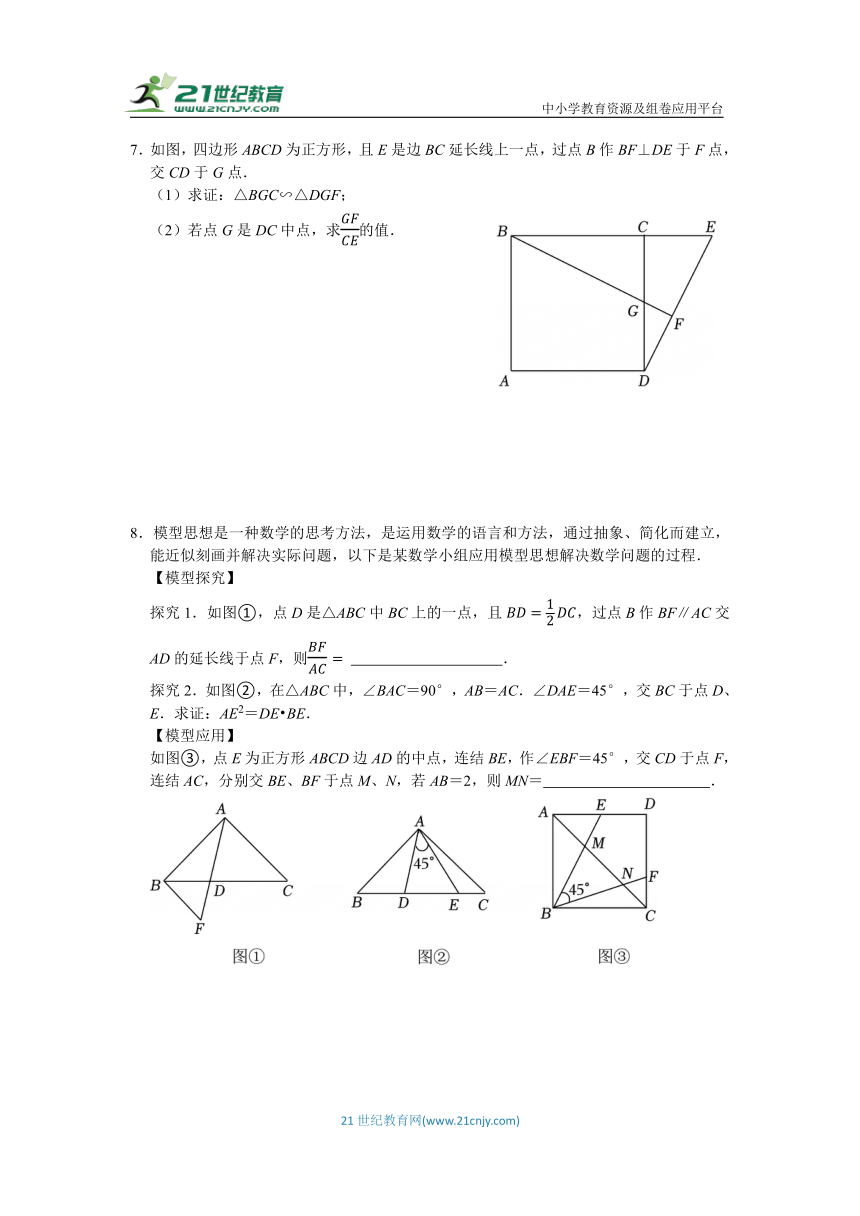
(1)如1,在正方形ABCD中,E,F分别是AB、AD上两点,连接DE,CF,若AE=DF,求证:△AED≌△DFC;
(2)在(1)的条件下,求证:DE⊥CF;
(3)如图2,在矩形ABCD中,过点C作CE⊥BD交AD于点E,若,求的值;
(4)如图3,在四边形ABCD中,∠A=∠B=90°,E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于F,且AB=5,AD=3,CF=6,求DE的长.
4.如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在边CD延长线上,且满足∠MAN=90°,联结MN,AC,MN与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=AC AE;
(3)MN交AC点O,若,则 (直接写答案、用含k的代数式表示).
5.如图,在正方形ABCD中,点E在CA的延长线上,将△ABE绕点B顺时针旋转90°至△CBG,EG与AD交于点F,与BC延长线交于点H,已知AE=4,EF=6.请解答以下问题:
(1)∠BCG的度数是 °;
(2)求证:BG2=BC BH;
(3)求GH的长.
6.如图1,E为凸四边形ABCD内一点,EC⊥CD,分别连接AC,DE,已知:∠BAC=∠EDC,AC⊥BC.
(1)求证:△ABC∽△DEC;
(2)连接BE,求证:tan∠BAC;
(3)如图2,延长BE交AD于点F,连接CF,若∠BAC=30°,AF=1,CF=3,求BF的长.
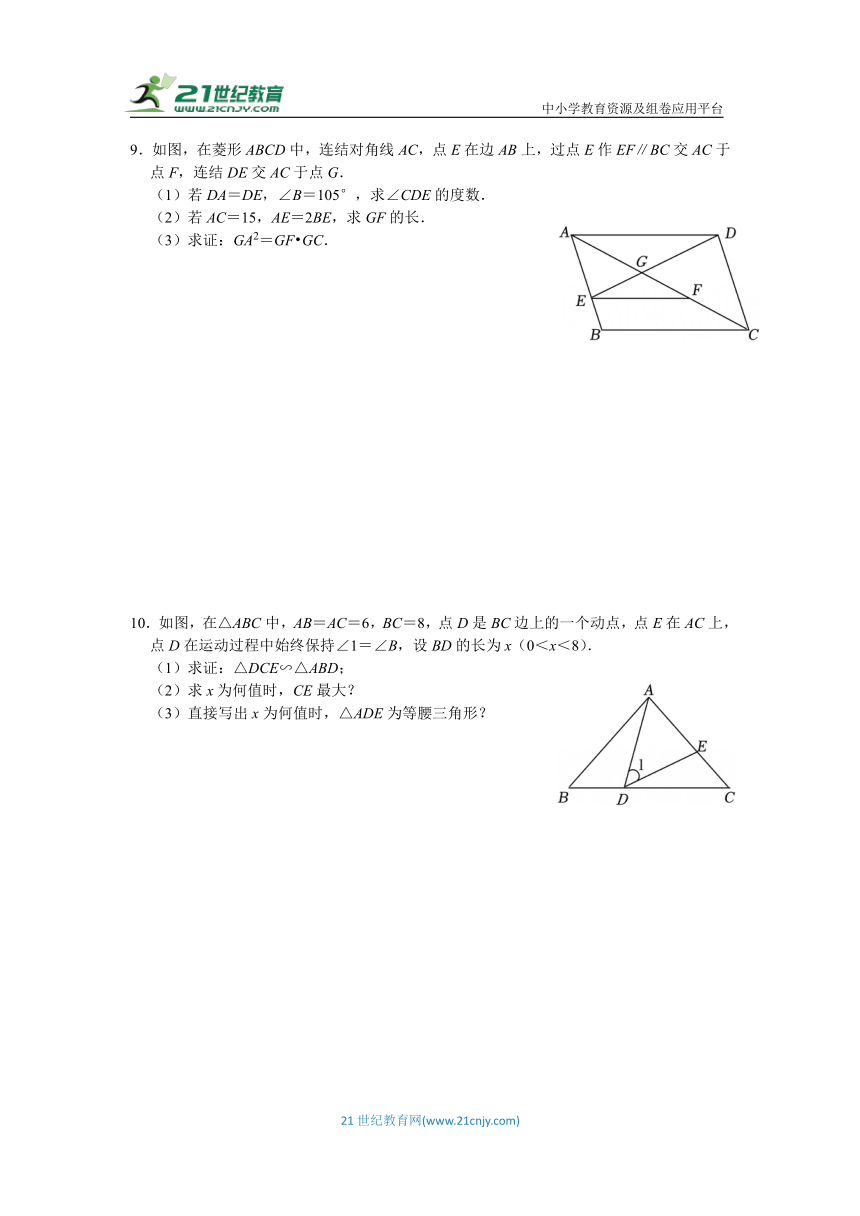
7.如图,四边形ABCD为正方形,且E是边BC延长线上一点,过点B作BF⊥DE于F点,交CD于G点.
(1)求证:△BGC∽△DGF;
(2)若点G是DC中点,求的值.
8.模型思想是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化而建立,能近似刻画并解决实际问题,以下是某数学小组应用模型思想解决数学问题的过程.
【模型探究】
探究1.如图①,点D是△ABC中BC上的一点,且,过点B作BF∥AC交AD的延长线于点F,则 .
探究2.如图②,在△ABC中,∠BAC=90°,AB=AC.∠DAE=45°,交BC于点D、E.求证:AE2=DE BE.
【模型应用】
如图③,点E为正方形ABCD边AD的中点,连结BE,作∠EBF=45°,交CD于点F,连结AC,分别交BE、BF于点M、N,若AB=2,则MN= .
9.如图,在菱形ABCD中,连结对角线AC,点E在边AB上,过点E作EF∥BC交AC于点F,连结DE交AC于点G.
(1)若DA=DE,∠B=105°,求∠CDE的度数.
(2)若AC=15,AE=2BE,求GF的长.
(3)求证:GA2=GF GC.
10.如图,在△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC上,点D在运动过程中始终保持∠1=∠B,设BD的长为x(0<x<8).
(1)求证:△DCE∽△ABD;
(2)求x为何值时,CE最大?
(3)直接写出x为何值时,△ADE为等腰三角形?
11.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D是线段AC上的点,且满足tan∠ADB=3,将线段DB绕点D逆时针旋转90°得到DE,连结CE.
(1)求证:AC⊥CE;
(2)连结DE交线段BC于点F,求的值;
(3)点P在直线AC上,当时,求AP的长.
12.△ABC中,∠ABC=90°,BD⊥AC,点E为BD的中点,连接AE并延长交BC于点F,且有AF=CF,过F点作FH⊥AC于点H.
(1)求证:△ADE∽△CDB;
(2)求证:AE=2EF;
(3)若FH,求BC的长.
13.如图,矩形ABCD中,AB=mBC,E是AB上一点,连结DE,过点D作DF⊥DE交直线BC于点F,连结EF交CD于点G,作DM⊥EF交EF于点M,交直线AB于点N.
(1)若m=1,求值.
(2)设tan∠BFE=k.
①若,求的值.(用含m的代数式表示)
②若△DMG的面积为S1,△EMN的面积为S2,求的值.(用含m,k的代数式表示)
14.正方形ABCD边长为2,点E在边BC上.将△ABE沿AE翻折至△AEF,延长EF交CD于点G,连接AG.
(1)如图1,求证:∠DAG=∠FAG;
(2)当点E是BC中点时,
①如图2,求tan∠CGE的值;
②如图3,连接BD,取BD中点O,连接OF并延长交CD于点M.求的值.
15.如图,AD∥BC,点E在边AB上.
(1)如图1,点F在边CD上,若,求证:EF∥BC;
(2)如图2,若,点M在边BC上,DM,CE相交于点N,已知CD2=DM DN,∠CEM=∠DMC.
①判断四边形ABMD的形状;
②求线段CD的长.
16.如图,在矩形ABCD中,AB=6,BC=8,点P在射线AD上运动,以BP为直角边向右作Rt△PBQ,使得∠BPQ=90°,BP=2PQ,连接CQ.
(1)若△ABP与△BPQ相似,则AP= ;
(2)当AP=2时,求CQ的值;
(3)求CQ的最小值.
17.如图,在正方形ABCD中,M为BC边上一动点(点M不与B,C重合),连接DM,将线段DM绕点M逆时针旋转90°得到线段MN,连接BD、BN、DN,DN交AB边于点P.
(1)如图1,求证:△DCM∽△DBN;
(2)如图2,设,,
①当x=1时,请探究得出y的值;
②求出y与x之间满足的关系式.并解决问题:如图3所示,连接MP,若,当∠PMN=30°时,求CM的长.
18.如图,菱形ABCD中,∠A=60°,点E在对角线BD上,且BE=3DE,点F为边AB上一动点,作∠FEP=60°,交BC于点P,交AB延长线于点G.
(1)求证:△EFB∽△GFE;
(2)连接PF,求证:△EFP是等边三角形;
(3)连接PF,延长FE交CD于点Q,连接PQ,当△PEQ与△BFP相似时,求的值.
参考答案
1.【解答】(1)证明:∵DE⊥CM,
∴∠CDF+∠DCF=90°,
∵∠ACB=90°,点M为AB的中点,
∴,
∴∠B=∠BCM,
∵∠BCM+∠DCF=90°,
∴∠CDF=∠BCM=∠B,
又∵∠BCA=∠DCE,
∴△CDE∽△CBA;
(2)证明:由(1)可知,,△CDE∽△CBA,
∵DE=CM,
∴,
∴,
即BC=2DC;
(3)解:过点A作AP⊥CM于点P,过点B作BQ⊥CM交CM延长线于点Q,如图2,
∵DE⊥CM,AP⊥CM,BQ⊥CM,
∴AP∥DE∥BQ,
∴,,
∵点M为AB的中点,
∴AM=BM,
∵∠AMP=∠BMQ,∠Q=∠APM,
在△AMP和△BMQ中,
,
∴△AMP≌△BMQ(AAS),
∴PM=QM,
∵点F为CM的中点,
∴,
∴
=2.
2.【解答】(1)证明:∵矩形ABCD,
∴∠BAD=90°,
∴∠ABE+∠AEB=90°,
∵∠ABE=∠DAF,
∴∠DAF+∠AEB=90°,
∴∠AOE=90°,
∴AF⊥BE;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABF=∠GDF,∠BAF=∠DGF,
∴△ABF∽△GDF,
∴,
∴,
∴,
∵四边形ABCD是矩形,
∴∠BAE=∠ADG=90°,
∵∠ABE=∠DAF,
∴△ABE∽△DAG,
∴,
∵AB=4,AD=6,DG=2,
∴,
∴,
故答案为:;
(3)解:∵正方形ABCD,
∴∠ABF=∠GDF,∠BAF=∠DGF,
∴△ABF∽△GDF,
∴.
∵,
∴,
设正方形ABCD的边长为a,则AB=AD=a,
∴,AF=2GF,
∴,
∵AF=2GF,
∴,
∴,
故答案为:.
3.【解答】(1)证明:由正方形可知∠A=∠FDC=90°,AD=CD,
在△AED与△DFC中,
,
∴△AED≌△DFC(SAS);
(2)证明:由正方形性质可知∠ADE+∠AED=90°,
∵△AED≌△DFC(AAS),
∴∠DFC=∠AED,
∴∠DFC+∠ADE=90°,
∴DE⊥CF;
(3)解:如图2,设BD与CE交于点G,
由条件可知∠A=∠EDC=90°,AB=CD,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
∵,
∴;
(4)解:如图3,过点C作CH⊥AF交AF的延长线于点H,
由条件可知∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴,
∴.
4.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠CAD=45°=∠ACB,∠BAD=90°=∠CDA=∠B,
∴∠BAM+∠MAD=90°,
∵∠MAN=90°,
∴∠MAD+∠DAN=90°,
∴∠BAM=∠DAN,
∵AD=AB,∠ABC=∠ADN=90°,
∴△ABM≌△ADN(ASA),
∴AM=AN;
(2)证明:∵AM=AN,∠MAN=90°,
∴∠MNA=45°,
∵∠CAD=2∠NAD=45°,
∴∠NAD=22.5°,
∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°,
∴∠CAM=∠NAD,∠ACB=∠MNA=45°,
∴△AMC∽△AEN,
∴,
∴AM AN=AC AE,
∵AN=AM,
∴AM2=AC AE;
(3)解:如图,过点M作MF∥AB交AC于点F,
设BM=a,
∵k,
∴BM=a,BC=(k+1)a,
即ND=BM=a,AB=CD=BC=(k+1)a,
∵MF∥AB∥CD,
∴,
∴MF=ka,
∴.
故答案为:.
5.【解答】(1)解:∵△ABE绕点B顺时针旋转90°至△CBG,
∴BE=BG,∠EBA=∠GBC,△ABE≌△CBG,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴∠BAE=180°﹣∠BAC=135°,
∵△ABE≌△CBG,
∴∠BCG=∠BAE=135°,
故答案为:135°;
(2)证明:∵△ABE绕点B顺时针旋转90°至△CBG,
∴∠EBA=∠GBC,
∴∠EBA+∠ABG=∠ABG+∠GBC=∠ABC=90°,
∴∠EBG=90°,
又∵BE=BG,
∴∠BGE=45°,
∴∠BGH=135°,
在△BCG和△BGH中,∠GBC=∠HBG,∠BCG=∠BGH=135°,
∴△BCG∽△BGH,
∴,
∴BG2=BC BH;
(3)解:∵△BCG∽△BGH,
∴△BAE∽△BGH,
∴∠BEA=∠H,
∵四边形ABCD是正方形,AC是正方形ABCD的对角线,AE=4,EF=6,
∴AD∥BH,∠DAC=∠BCA=45°
∴∠H=∠EFA,∠EAF=135°,
∴∠BEA=∠EFA,∠EAF=∠BAE,
∴△BAE∽△EAF,
∴,
设AB=2x,BE=3x,
则有AB=BC=2x,BE=BG=3x,
在直角三角形BEG中,由勾股定理得:,
在直角三角形ABC中,由勾股定理得:,
∴,
∵∠BCG=135°,
∴∠HCG=45°,
∴∠ECG=180°﹣∠BCA﹣∠HCG=90°,
在Rt△ECG中,由勾股定理得:EG2=CG2+EC2,
由旋转可知CG=AE=4,
∴
解得:,(负值,舍去),
∴,
∴,
又∵AF∥CH,
∴,
∴,
∴.
6.【解答】(1)证明:E为凸四边形ABCD内一点,EC⊥CD,AC⊥BC,∠BAC=∠EDC,
∴∠ACB=∠ECD=90°,
∴△ABC∽△DEC;
(2)证明:由(1)知:△ABC∽△DEC,
∴,
∴,
∵∠ACB=∠ECD=90°,
∴∠BCE=∠ACD=90°﹣∠ACE,
∴△BCE∽△ACD,
∴,
在Rt△ABC中,,
∴;
(3)解:∠BAC=30°,AF=1,CF=3,如图2,过点C作CG⊥CF,则∠GCF=∠ACB=90°,
∴∠BCG=∠ACF=90°﹣∠ACG,
∵△BCE∽△ACD,
∴∠CBE=∠CAF,
∴△BCG∽△ACF,
∴,
∵,
∴,
∴,
在直角三角形CFG中,由勾股定理得:,
∴.
7.【解答】(1)证明:∵四边形ABCD为正方形,且E是边BC延长线上一点,BF⊥DE于F点,
∴∠BCG=∠DFG=90°,
又∵∠BGC=∠DGF,
∴△BGC∽△DGF;
(2)解:∵∠DCE=∠DFG=90°,∠CDE=∠FDG,
∴△DCE∽△DFG,
由(1)得△BGC∽△DGF,且点G是DC中点,
∴,
设BC=2a,则CG=a.
在Rt△BCG中,由勾股定理得:,
故.
8.【解答】【模型探究】
探究1.解:∵BF∥AC,
∴△BDF∽△CDA,
∴,
∵,
∴,
故答案为:;
探究2.证明:在Rt△ABC中,
∵AB=AC,
∴∠B=∠DAE=45°.
又∵∠AEB=∠BEA,
∴△ADE∽△BAE.
∴,
∴AE2=DE BE;
【模型应用】解:∵四边形ABCD是正方形,
∴AD=AB=BC=2,∠BAC=∠ACB=45°,∠ABC=90°,
∴ACAB=2,
∵点E为正方形ABCD边AD的中点,
∴AE1,
∴BE,
∵AD∥BC,
∴△AME∽△CMB,
∴,
∴,
∴BM,CM,
∵∠MBN=∠BCM=45°,∠BMN=∠CMB,
∴△BMN∽△CMB,
∴,
∴,
∴MN,
故答案为:.
9.【解答】(1)解:∵∠B=105°,AD∥BC,
∴∠BAD=75°,
∵DA=DE,
∴∠AED=∠BAD=75°,
∴∠ADE=30°,
由菱形对角相等可得∠ADC=∠B=105°,
∴∠CDE=105°﹣30°=75°.
(2)解:∵EF∥BC,
∴,
又∵AC=15,
∴AF10,
由EF∥BC,可得△AEF∽△ABC,
∴,
又∵BC=AD,
∴,
∵EF∥AD,
∴△GEF∽△GDA,
∴,
故GF4.
(3)证明:由菱形性质知∠DAC=∠BAC,
又∵EF∥AD,
∴∠DAC=∠AFE,
∴∠BAC=∠AFE,
∴AE=EF.
∵DC∥AB,
∴△AGE∽△CGD,
∴,
由(2)中知,
∴,
∴GA2=GF GC.
10.【解答】(1)证明:如图,
∵∠ADC=∠1+∠2=∠B+∠3,∠1=∠B,
∴∠2=∠3.
又∵AB=AC,
∴∠B=∠C,
∴△DCE∽△ABD;
(2)解:∵△DCE∽△ABD,
∴,即,
∴,
∵,
∴CE有最大值,
∴当x=4时,CE有最大值;
(3)解:当x=2或时,△ADE为等腰三角形.理由如下:
①当DA=DE时,
∵∠2=∠3,∠C=∠B,
在△DCE和△ABD中,
,
∴△DCE≌△ABD(AAS),
∴DC=AB=6,即8﹣x=6,
解得 x=2.
②当EA=ED时,∠DAE=∠1=∠B=∠C.
∴△DAC∽△ABC.
∴,即.
解得 .
③当AD=AE时,点D与点B重合,点E与点C重合,此时x=0.
或当AD=AE时,∠1=∠AED>∠C,
∵∠1=∠B=∠C,
∴AD=AE情况不成立.
综上所述,当x=2或时,△ADE为等腰三角形.
11.【解答】(1)证明:在Rt△ABC中,∠A=90°,
∵tan,AB=3,
∴AD=1,CD=AC﹣AD=3,
由旋转的性质得:DB=DE,
∴∠ADB+∠ABD=∠ADB+∠CDE=90°,
∴∠ABD=∠CDE,
在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴∠DCE=∠BAD=90°,
∴AC⊥CE;
(2)解:如图2,过点D作DG∥AB交BC于点G,
∴△CDG∽△CAB,
∴,
即
∴,
由(1)知CE∥AB,CE=AD=1,
∴DG∥CE,
∴△CEF∽△GDF,
∴,
即,
∴,
∵BD=ED,
∴,
(3)解:在Rt△ADB中,,
①当点P在点D下方时,
如图3,连结PB,过点P作PM⊥BD于点M,
在Rt△PBM中,tan,
设PM=a,则BM=2a,
在Rt△PDM和Rt△ADB中,
tan,
∴,
∵BD=DM+BM,
∴,
解得,
∴,
在Rt△ADB中,sin,
在Rt△PDM中,sin,
∴,
∴,
∴,
②当点P在点D上方时,
如图4,连结PB,过点P作PN⊥BD交BD的延长线于点N
在Rt△PBN中,tan,
设PN=b,则BN=2b,
∵∠ADB=∠NDP,
∴tan∠ADB=tan∠NDP,
∴,
∴,
∴,
∴,
∵∠ADB=∠NDP,
∴sin∠ADB=sin∠NDP,
∴,
∴,
∴AP=DP+AD=3,
综上所述:AP的长为.
12.【解答】证明:(1)∵BD⊥AC,FH⊥AC,
∴∠ADE=∠CDB=90°,BD∥FH,
∵AF=CF,
∴∠DAE=∠DCB,
在△ADE与△CDB中,
∠ADE=∠CDB,∠DAE=∠DCB,
∴△ADE∽△CDB;
(2)∵点E为BD的中点,
∴DE=BE,
∵△ADE∽△CDB,
∴,
设AD=a(a>0),则CD=2a,AC=AD+CD=3a,
∵FH⊥AC,AF=CF,
∴AH=CH,
又∵BD∥FH,
∴,
即AE=2EF;
(3)解:由(2)知,AE=2EF,
∴AE,
∵BD∥FH,
∴△ADE∽△AHF,
∴,
即,
解得:DE,
∴BD=2DE,
∵∠ABC=90°,BD⊥AC,
∴∠BAC+∠ABD=∠BAC+∠C=90°,
∴∠ABD=∠C,
∵∠ADB=∠BDC,∠ABD=∠C,
∴△ABD∽△BCD,
∴,
由(2)知,设AD=b(b>0),则CD=2b,
∴,
解得:b或(舍去),
∴CD=2b,
在Rt△BCD中,BC4.
13.【解答】解:(1)∵矩形ABCD,AB=mBC,
∴,∠EDF=∠ADC=90°,
∴∠ADE=∠CDF=90°﹣∠EDC,
∵∠DAE=∠DCF=90°,
∴△ADE∽△CDF,
∴;
(2)①∵DM⊥EF,
∴∠DMG=∠FCG=90°,
∵∠DGM=∠FGC,
∴∠MDG=∠CFG,
∴,,
∴,
即,
∴,
∴,
∴;
②由(1)得,∠EDF=90°,
∴,,
∴,
∵CD∥AB,
∴△DMG∽△NME,
∴.
14.【解答】(1)证明:∵正方形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
由翻折变换的性质可知AB=AF,∠B=∠AFE=90°,
∴AF=AD,∠AFG=∠D=90°,
∵AG=AG,
∴Rt△AGD≌Rt△AGF(HL),
∴∠DAG=∠FAG;
(2)解:①由(1)可知△AGD≌△AGF,
∴GD=GF,
∵E是BC的中点,
∴BE=CE=EF=1,
设GD=GF=x,
在Rt△CGE中,EG2=CG2+EC2,
∴(1+x)2=(2﹣x)2+12,
∴x,
∴CG=2,
∴tan∠CGE;
②如图3中,连接BF,CF,BF交AE于点J,过点F作FH⊥BC于点H.
∵AB=2,BE=1,∠ABE=90°,
∴AE,
由翻折变换的性质可知,AB=AF=2,BE=EF=1,
∴AE垂直平分线段BF,
∴BJ=JF,
∵ AB BE AE BJ,
∴BJ,
∴BF,
∵∠FBC+∠ABF=90°,∠ABF+∠BAE=90°,
∴∠BAE=∠FBC,
∴tan∠FBC=tan∠BAE,
∴,
∴,
∴CF,
∵ BF CF BC FH,
∴FH,
∴CH,
∴EH=CE﹣CH=1,
∵OE∥FH∥CM,
∴.
15.【解答】(1)证明:连接DE,并延长DE,交CB的延长线于点G,
∵AD∥BC,
∴△ADE∽△BGE,
∴,
∴,即,
∵,
∴,
∵∠EDF=∠GDC,
∴△DEF∽△DGC,
∴∠DEF=∠DGC,
∴EF∥GC,即EF∥BC.
(2)解:①四边形ABMD是平行四边形;理由如下:
如图2,延长BA,CD相交于点P,
∵,
∴AB=2,BC=3,
∵AD∥BC,
∴△PAD∽△PBC,
∴,即,
∴PA=1,
∴BP=BE+AE+AP=1+1+1=3.
∵CD2=DM DN,
∴,
∵∠CDN=∠MDC,
∴△CDN∽△MDC,
∴∠DCN=∠DMC,
∵∠CEM=∠DMC,
∴∠DCN=∠CEM,
∴EM∥CD,
∴△BEM∽△BPC,
∴,即,
∴BM=1,
∴BM=AD,
∵AD∥BM,
∴四边形ABMD是平行四边形.
②延长BA,CD相交于点P,如图3,
∵△PAD∽△PBC,
∴,
∴,
∴,
∵△BEM∽△BPC,
∴,即,
∴,
∴,
∵EM∥CD,
∴△EMN∽△CDN,
∴,
设EN=a,则CN=2a,EC=EN+CN=3a,
∵∠MEC=∠NMC,∠ECM=∠MCN,
∴△ECM∽△MCN,
∴,即,
解得,
∴.
延长BA,CD相交于点P,过点E作EQ⊥BC于点Q,
设MQ=x,则BQ=BM﹣MQ=1﹣x,CQ=QM+MC=x+2,
在Rt△BEQ中,由勾股定理得:EQ2=BE2﹣BQ2,
在Rt△CEQ中,由勾股定理得:EQ2=EC2﹣CQ2,
∴BE2﹣BQ2=EC2﹣CQ2,
∴,
解得,
∴,,
在Rt△BEQ中,由勾股定理得:,
在Rt△EQM中,由勾股定理得:,
∵,
∴.
16.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=90°,
∴∠BPQ=∠A=90°,
∵△ABP与△BPQ相似,
∴或,
∵AB=6,BP=2PQ,
∴或,
∴AP=3或AP=12,
故答案为:3或12;
(2)解:过点Q作MN⊥AD于点M,与BC交于点N,
则∠A=∠PMQ=∠CNQ=90°,AB=MN=6,
∵∠BPQ=90°,
∴∠APB+∠MPQ=∠MPQ+∠PQM=90°,
∴∠APB=∠MQP,
∴△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,AP=2,
∴2,
∴x=1,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2=3,
∴CQ2=QN2+CN2=52+32=34,
∴CQ;
(3)由(2)得,△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,
∴2,
∴AP=2x,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2x=5﹣2x,
∴CQ2=QN2+CN2=(6﹣x)2+(5﹣2x)2,
=5(x)2,
当x时,CQ2的最小值为,
∴CQ长的最小值为.
17.【解答】(1)证明:如图1中,过点N作NH⊥CB交CB的延长线于点H.
∵MD=MN,∠DMN=90°,
∴△DMN是等腰直角三角形,
∴∠MDN=45°,
∵四边形ABCD是正方形,
∴CD=CB,∠C=∠ABC=90°,∠BDC=∠DBC=45°,
∵NH⊥CH,
∴∠H=∠DCM=90°,
∵∠NMH+∠DMC=90°,∠DMC+∠CDM=90°,
∴∠NMH=∠CDM,
∵MD=MN,
∴△DCM≌△MHN(AAS),
∴CD=MH=BC,CM=NH,
∴BH=CM=NH,
∴∠NBH=45°,
∴∠DBN=∠DCM=90°,
∵∠NDM=∠BDC,
∴∠NDB=∠MDC,
∴△DCM∽△DBN;
(2)解:①如图2中,过点P作PE⊥BD于点E,PF⊥BN于点F,NH⊥CB交CB的延长线于点H.
当x=1时,设CM=BM=a,则BD=2a,
由(1)可知NH=BH=CM=a,
∴BNa,
∵∠PBN=∠PBD=45°,PE⊥BD.PF⊥BN,
∴PE=PF,
∴,
∴,
∴y;
②如图3中,延长BC到T,使得CT=AP.
∵AD=CD,∠DAP=∠DCT=90°,AP=CT,
∴△DAP≌△DCT(SAS),
∴∠ADP=∠CDT,DP=DT,
∴∠PDT=∠ADC=90°,
∵∠PDM=45°,
∴∠PDM=∠TDM,
∵DM=DM,
∴△DMP≌△DMT(SAS),
∴∠DMP=∠DMT,
∵∠PMN=30°,∠DMN=90°,
∴∠DMT=∠DMP=90°﹣30°=60°,
∵CD=AB=2,
∴tan60°,
∴,
∴CM=2.
18.【解答】(1)证明:∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD为等边三角形,
∴∠ABD=60°,
∴∠G+∠BEP=60°,
∵∠FEP=60°=∠BEF+∠BEP,
∴∠BEF=∠G,
又∵∠BFE=∠EFG,
∴△EFB∽△GFE;
(2)证明:方法一:如图,过E作EM∥AD交AB于点M,则∠EMF=∠A=60°,
由(1)可知∠EBM=60°,
∴△EBM是等边三角形,
∴EM=EB,
∴EM=EB,∠MEB=60°,
∵∠FEP=60°,‘
∴∠MEF=∠BEP,
在△EMF和△EBP中,
,
∴△EMF≌△EBP(AAS),
∴EF=EP,
∴△EFP是等边三角形;
方法二:如图,过E作EM⊥AB于点M,作EN⊥BC于点N,则∠EMB=∠ENB=90°,
∵四边形ABCD是菱形,
∴BD平分∠ABC,∠ABC=120°,
∴∠EM=EN,
∵∠FEP=60°,
∴∠ABC+∠FEP=180°,
∴∠EFM+∠EPB=180°,
∵∠EPN+∠EPB=180°,
∴∠EFM=∠EPN,
在△EFM和△EPN中,
,
∴△EFM≌△EPN(AAS),
∴EF=EP,
∴△EFP是等边三角形;
(3)解:过E作EM∥AD交AB于点M,
设DE=1,FM=x,则BE=3,
∵△ABD是等边三角形,
∴AM=1,BM=3,
∴BF=3﹣x,
由(2)知△EMF≌△EBP,
∴BP=FM=x,
∵DC∥BF,
∴,
∵EF=EP,
∴,
∵∠FEP=60°,
∴∠PEQ=120°=∠PBF,
∴当△PEQ与△BFP相似时可以分两种情况讨论,
①△PEQ∽△FBP,
此时,
∴,
∴,
解得x,
由(1)知△EFB∽△GFE,
∴;
②△PEQ∽△PBF,
此时,
即,
解得x,
∴;
综上,的值为或.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习图形的相似综合问题
1.在Rt△ABC中,∠ACB=90°,点M为AB的中点,点F是线段CM上一动点,过点F作DE⊥CM分别交边CA,CB于点D,E.
(1)如图1,求证△CDE∽△CBA;
(2)如图1,若DE=CM,求证:BC=2DC;
(3)如图2,若点F为CM的中点,求的值.
2.如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=4,AD=6,,求AE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,,直接写出的值.
3.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如1,在正方形ABCD中,E,F分别是AB、AD上两点,连接DE,CF,若AE=DF,求证:△AED≌△DFC;
(2)在(1)的条件下,求证:DE⊥CF;
(3)如图2,在矩形ABCD中,过点C作CE⊥BD交AD于点E,若,求的值;
(4)如图3,在四边形ABCD中,∠A=∠B=90°,E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于F,且AB=5,AD=3,CF=6,求DE的长.
4.如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在边CD延长线上,且满足∠MAN=90°,联结MN,AC,MN与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=AC AE;
(3)MN交AC点O,若,则 (直接写答案、用含k的代数式表示).
5.如图,在正方形ABCD中,点E在CA的延长线上,将△ABE绕点B顺时针旋转90°至△CBG,EG与AD交于点F,与BC延长线交于点H,已知AE=4,EF=6.请解答以下问题:
(1)∠BCG的度数是 °;
(2)求证:BG2=BC BH;
(3)求GH的长.
6.如图1,E为凸四边形ABCD内一点,EC⊥CD,分别连接AC,DE,已知:∠BAC=∠EDC,AC⊥BC.
(1)求证:△ABC∽△DEC;
(2)连接BE,求证:tan∠BAC;
(3)如图2,延长BE交AD于点F,连接CF,若∠BAC=30°,AF=1,CF=3,求BF的长.
7.如图,四边形ABCD为正方形,且E是边BC延长线上一点,过点B作BF⊥DE于F点,交CD于G点.
(1)求证:△BGC∽△DGF;
(2)若点G是DC中点,求的值.
8.模型思想是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化而建立,能近似刻画并解决实际问题,以下是某数学小组应用模型思想解决数学问题的过程.
【模型探究】
探究1.如图①,点D是△ABC中BC上的一点,且,过点B作BF∥AC交AD的延长线于点F,则 .
探究2.如图②,在△ABC中,∠BAC=90°,AB=AC.∠DAE=45°,交BC于点D、E.求证:AE2=DE BE.
【模型应用】
如图③,点E为正方形ABCD边AD的中点,连结BE,作∠EBF=45°,交CD于点F,连结AC,分别交BE、BF于点M、N,若AB=2,则MN= .
9.如图,在菱形ABCD中,连结对角线AC,点E在边AB上,过点E作EF∥BC交AC于点F,连结DE交AC于点G.
(1)若DA=DE,∠B=105°,求∠CDE的度数.
(2)若AC=15,AE=2BE,求GF的长.
(3)求证:GA2=GF GC.
10.如图,在△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC上,点D在运动过程中始终保持∠1=∠B,设BD的长为x(0<x<8).
(1)求证:△DCE∽△ABD;
(2)求x为何值时,CE最大?
(3)直接写出x为何值时,△ADE为等腰三角形?
11.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D是线段AC上的点,且满足tan∠ADB=3,将线段DB绕点D逆时针旋转90°得到DE,连结CE.
(1)求证:AC⊥CE;
(2)连结DE交线段BC于点F,求的值;
(3)点P在直线AC上,当时,求AP的长.
12.△ABC中,∠ABC=90°,BD⊥AC,点E为BD的中点,连接AE并延长交BC于点F,且有AF=CF,过F点作FH⊥AC于点H.
(1)求证:△ADE∽△CDB;
(2)求证:AE=2EF;
(3)若FH,求BC的长.
13.如图,矩形ABCD中,AB=mBC,E是AB上一点,连结DE,过点D作DF⊥DE交直线BC于点F,连结EF交CD于点G,作DM⊥EF交EF于点M,交直线AB于点N.
(1)若m=1,求值.
(2)设tan∠BFE=k.
①若,求的值.(用含m的代数式表示)
②若△DMG的面积为S1,△EMN的面积为S2,求的值.(用含m,k的代数式表示)
14.正方形ABCD边长为2,点E在边BC上.将△ABE沿AE翻折至△AEF,延长EF交CD于点G,连接AG.
(1)如图1,求证:∠DAG=∠FAG;
(2)当点E是BC中点时,
①如图2,求tan∠CGE的值;
②如图3,连接BD,取BD中点O,连接OF并延长交CD于点M.求的值.
15.如图,AD∥BC,点E在边AB上.
(1)如图1,点F在边CD上,若,求证:EF∥BC;
(2)如图2,若,点M在边BC上,DM,CE相交于点N,已知CD2=DM DN,∠CEM=∠DMC.
①判断四边形ABMD的形状;
②求线段CD的长.
16.如图,在矩形ABCD中,AB=6,BC=8,点P在射线AD上运动,以BP为直角边向右作Rt△PBQ,使得∠BPQ=90°,BP=2PQ,连接CQ.
(1)若△ABP与△BPQ相似,则AP= ;
(2)当AP=2时,求CQ的值;
(3)求CQ的最小值.
17.如图,在正方形ABCD中,M为BC边上一动点(点M不与B,C重合),连接DM,将线段DM绕点M逆时针旋转90°得到线段MN,连接BD、BN、DN,DN交AB边于点P.
(1)如图1,求证:△DCM∽△DBN;
(2)如图2,设,,
①当x=1时,请探究得出y的值;
②求出y与x之间满足的关系式.并解决问题:如图3所示,连接MP,若,当∠PMN=30°时,求CM的长.
18.如图,菱形ABCD中,∠A=60°,点E在对角线BD上,且BE=3DE,点F为边AB上一动点,作∠FEP=60°,交BC于点P,交AB延长线于点G.
(1)求证:△EFB∽△GFE;
(2)连接PF,求证:△EFP是等边三角形;
(3)连接PF,延长FE交CD于点Q,连接PQ,当△PEQ与△BFP相似时,求的值.
参考答案
1.【解答】(1)证明:∵DE⊥CM,
∴∠CDF+∠DCF=90°,
∵∠ACB=90°,点M为AB的中点,
∴,
∴∠B=∠BCM,
∵∠BCM+∠DCF=90°,
∴∠CDF=∠BCM=∠B,
又∵∠BCA=∠DCE,
∴△CDE∽△CBA;
(2)证明:由(1)可知,,△CDE∽△CBA,
∵DE=CM,
∴,
∴,
即BC=2DC;
(3)解:过点A作AP⊥CM于点P,过点B作BQ⊥CM交CM延长线于点Q,如图2,
∵DE⊥CM,AP⊥CM,BQ⊥CM,
∴AP∥DE∥BQ,
∴,,
∵点M为AB的中点,
∴AM=BM,
∵∠AMP=∠BMQ,∠Q=∠APM,
在△AMP和△BMQ中,
,
∴△AMP≌△BMQ(AAS),
∴PM=QM,
∵点F为CM的中点,
∴,
∴
=2.
2.【解答】(1)证明:∵矩形ABCD,
∴∠BAD=90°,
∴∠ABE+∠AEB=90°,
∵∠ABE=∠DAF,
∴∠DAF+∠AEB=90°,
∴∠AOE=90°,
∴AF⊥BE;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ABF=∠GDF,∠BAF=∠DGF,
∴△ABF∽△GDF,
∴,
∴,
∴,
∵四边形ABCD是矩形,
∴∠BAE=∠ADG=90°,
∵∠ABE=∠DAF,
∴△ABE∽△DAG,
∴,
∵AB=4,AD=6,DG=2,
∴,
∴,
故答案为:;
(3)解:∵正方形ABCD,
∴∠ABF=∠GDF,∠BAF=∠DGF,
∴△ABF∽△GDF,
∴.
∵,
∴,
设正方形ABCD的边长为a,则AB=AD=a,
∴,AF=2GF,
∴,
∵AF=2GF,
∴,
∴,
故答案为:.
3.【解答】(1)证明:由正方形可知∠A=∠FDC=90°,AD=CD,
在△AED与△DFC中,
,
∴△AED≌△DFC(SAS);
(2)证明:由正方形性质可知∠ADE+∠AED=90°,
∵△AED≌△DFC(AAS),
∴∠DFC=∠AED,
∴∠DFC+∠ADE=90°,
∴DE⊥CF;
(3)解:如图2,设BD与CE交于点G,
由条件可知∠A=∠EDC=90°,AB=CD,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
∵,
∴;
(4)解:如图3,过点C作CH⊥AF交AF的延长线于点H,
由条件可知∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴,
∴.
4.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠CAD=45°=∠ACB,∠BAD=90°=∠CDA=∠B,
∴∠BAM+∠MAD=90°,
∵∠MAN=90°,
∴∠MAD+∠DAN=90°,
∴∠BAM=∠DAN,
∵AD=AB,∠ABC=∠ADN=90°,
∴△ABM≌△ADN(ASA),
∴AM=AN;
(2)证明:∵AM=AN,∠MAN=90°,
∴∠MNA=45°,
∵∠CAD=2∠NAD=45°,
∴∠NAD=22.5°,
∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°,
∴∠CAM=∠NAD,∠ACB=∠MNA=45°,
∴△AMC∽△AEN,
∴,
∴AM AN=AC AE,
∵AN=AM,
∴AM2=AC AE;
(3)解:如图,过点M作MF∥AB交AC于点F,
设BM=a,
∵k,
∴BM=a,BC=(k+1)a,
即ND=BM=a,AB=CD=BC=(k+1)a,
∵MF∥AB∥CD,
∴,
∴MF=ka,
∴.
故答案为:.
5.【解答】(1)解:∵△ABE绕点B顺时针旋转90°至△CBG,
∴BE=BG,∠EBA=∠GBC,△ABE≌△CBG,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴∠BAE=180°﹣∠BAC=135°,
∵△ABE≌△CBG,
∴∠BCG=∠BAE=135°,
故答案为:135°;
(2)证明:∵△ABE绕点B顺时针旋转90°至△CBG,
∴∠EBA=∠GBC,
∴∠EBA+∠ABG=∠ABG+∠GBC=∠ABC=90°,
∴∠EBG=90°,
又∵BE=BG,
∴∠BGE=45°,
∴∠BGH=135°,
在△BCG和△BGH中,∠GBC=∠HBG,∠BCG=∠BGH=135°,
∴△BCG∽△BGH,
∴,
∴BG2=BC BH;
(3)解:∵△BCG∽△BGH,
∴△BAE∽△BGH,
∴∠BEA=∠H,
∵四边形ABCD是正方形,AC是正方形ABCD的对角线,AE=4,EF=6,
∴AD∥BH,∠DAC=∠BCA=45°
∴∠H=∠EFA,∠EAF=135°,
∴∠BEA=∠EFA,∠EAF=∠BAE,
∴△BAE∽△EAF,
∴,
设AB=2x,BE=3x,
则有AB=BC=2x,BE=BG=3x,
在直角三角形BEG中,由勾股定理得:,
在直角三角形ABC中,由勾股定理得:,
∴,
∵∠BCG=135°,
∴∠HCG=45°,
∴∠ECG=180°﹣∠BCA﹣∠HCG=90°,
在Rt△ECG中,由勾股定理得:EG2=CG2+EC2,
由旋转可知CG=AE=4,
∴
解得:,(负值,舍去),
∴,
∴,
又∵AF∥CH,
∴,
∴,
∴.
6.【解答】(1)证明:E为凸四边形ABCD内一点,EC⊥CD,AC⊥BC,∠BAC=∠EDC,
∴∠ACB=∠ECD=90°,
∴△ABC∽△DEC;
(2)证明:由(1)知:△ABC∽△DEC,
∴,
∴,
∵∠ACB=∠ECD=90°,
∴∠BCE=∠ACD=90°﹣∠ACE,
∴△BCE∽△ACD,
∴,
在Rt△ABC中,,
∴;
(3)解:∠BAC=30°,AF=1,CF=3,如图2,过点C作CG⊥CF,则∠GCF=∠ACB=90°,
∴∠BCG=∠ACF=90°﹣∠ACG,
∵△BCE∽△ACD,
∴∠CBE=∠CAF,
∴△BCG∽△ACF,
∴,
∵,
∴,
∴,
在直角三角形CFG中,由勾股定理得:,
∴.
7.【解答】(1)证明:∵四边形ABCD为正方形,且E是边BC延长线上一点,BF⊥DE于F点,
∴∠BCG=∠DFG=90°,
又∵∠BGC=∠DGF,
∴△BGC∽△DGF;
(2)解:∵∠DCE=∠DFG=90°,∠CDE=∠FDG,
∴△DCE∽△DFG,
由(1)得△BGC∽△DGF,且点G是DC中点,
∴,
设BC=2a,则CG=a.
在Rt△BCG中,由勾股定理得:,
故.
8.【解答】【模型探究】
探究1.解:∵BF∥AC,
∴△BDF∽△CDA,
∴,
∵,
∴,
故答案为:;
探究2.证明:在Rt△ABC中,
∵AB=AC,
∴∠B=∠DAE=45°.
又∵∠AEB=∠BEA,
∴△ADE∽△BAE.
∴,
∴AE2=DE BE;
【模型应用】解:∵四边形ABCD是正方形,
∴AD=AB=BC=2,∠BAC=∠ACB=45°,∠ABC=90°,
∴ACAB=2,
∵点E为正方形ABCD边AD的中点,
∴AE1,
∴BE,
∵AD∥BC,
∴△AME∽△CMB,
∴,
∴,
∴BM,CM,
∵∠MBN=∠BCM=45°,∠BMN=∠CMB,
∴△BMN∽△CMB,
∴,
∴,
∴MN,
故答案为:.
9.【解答】(1)解:∵∠B=105°,AD∥BC,
∴∠BAD=75°,
∵DA=DE,
∴∠AED=∠BAD=75°,
∴∠ADE=30°,
由菱形对角相等可得∠ADC=∠B=105°,
∴∠CDE=105°﹣30°=75°.
(2)解:∵EF∥BC,
∴,
又∵AC=15,
∴AF10,
由EF∥BC,可得△AEF∽△ABC,
∴,
又∵BC=AD,
∴,
∵EF∥AD,
∴△GEF∽△GDA,
∴,
故GF4.
(3)证明:由菱形性质知∠DAC=∠BAC,
又∵EF∥AD,
∴∠DAC=∠AFE,
∴∠BAC=∠AFE,
∴AE=EF.
∵DC∥AB,
∴△AGE∽△CGD,
∴,
由(2)中知,
∴,
∴GA2=GF GC.
10.【解答】(1)证明:如图,
∵∠ADC=∠1+∠2=∠B+∠3,∠1=∠B,
∴∠2=∠3.
又∵AB=AC,
∴∠B=∠C,
∴△DCE∽△ABD;
(2)解:∵△DCE∽△ABD,
∴,即,
∴,
∵,
∴CE有最大值,
∴当x=4时,CE有最大值;
(3)解:当x=2或时,△ADE为等腰三角形.理由如下:
①当DA=DE时,
∵∠2=∠3,∠C=∠B,
在△DCE和△ABD中,
,
∴△DCE≌△ABD(AAS),
∴DC=AB=6,即8﹣x=6,
解得 x=2.
②当EA=ED时,∠DAE=∠1=∠B=∠C.
∴△DAC∽△ABC.
∴,即.
解得 .
③当AD=AE时,点D与点B重合,点E与点C重合,此时x=0.
或当AD=AE时,∠1=∠AED>∠C,
∵∠1=∠B=∠C,
∴AD=AE情况不成立.
综上所述,当x=2或时,△ADE为等腰三角形.
11.【解答】(1)证明:在Rt△ABC中,∠A=90°,
∵tan,AB=3,
∴AD=1,CD=AC﹣AD=3,
由旋转的性质得:DB=DE,
∴∠ADB+∠ABD=∠ADB+∠CDE=90°,
∴∠ABD=∠CDE,
在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴∠DCE=∠BAD=90°,
∴AC⊥CE;
(2)解:如图2,过点D作DG∥AB交BC于点G,
∴△CDG∽△CAB,
∴,
即
∴,
由(1)知CE∥AB,CE=AD=1,
∴DG∥CE,
∴△CEF∽△GDF,
∴,
即,
∴,
∵BD=ED,
∴,
(3)解:在Rt△ADB中,,
①当点P在点D下方时,
如图3,连结PB,过点P作PM⊥BD于点M,
在Rt△PBM中,tan,
设PM=a,则BM=2a,
在Rt△PDM和Rt△ADB中,
tan,
∴,
∵BD=DM+BM,
∴,
解得,
∴,
在Rt△ADB中,sin,
在Rt△PDM中,sin,
∴,
∴,
∴,
②当点P在点D上方时,
如图4,连结PB,过点P作PN⊥BD交BD的延长线于点N
在Rt△PBN中,tan,
设PN=b,则BN=2b,
∵∠ADB=∠NDP,
∴tan∠ADB=tan∠NDP,
∴,
∴,
∴,
∴,
∵∠ADB=∠NDP,
∴sin∠ADB=sin∠NDP,
∴,
∴,
∴AP=DP+AD=3,
综上所述:AP的长为.
12.【解答】证明:(1)∵BD⊥AC,FH⊥AC,
∴∠ADE=∠CDB=90°,BD∥FH,
∵AF=CF,
∴∠DAE=∠DCB,
在△ADE与△CDB中,
∠ADE=∠CDB,∠DAE=∠DCB,
∴△ADE∽△CDB;
(2)∵点E为BD的中点,
∴DE=BE,
∵△ADE∽△CDB,
∴,
设AD=a(a>0),则CD=2a,AC=AD+CD=3a,
∵FH⊥AC,AF=CF,
∴AH=CH,
又∵BD∥FH,
∴,
即AE=2EF;
(3)解:由(2)知,AE=2EF,
∴AE,
∵BD∥FH,
∴△ADE∽△AHF,
∴,
即,
解得:DE,
∴BD=2DE,
∵∠ABC=90°,BD⊥AC,
∴∠BAC+∠ABD=∠BAC+∠C=90°,
∴∠ABD=∠C,
∵∠ADB=∠BDC,∠ABD=∠C,
∴△ABD∽△BCD,
∴,
由(2)知,设AD=b(b>0),则CD=2b,
∴,
解得:b或(舍去),
∴CD=2b,
在Rt△BCD中,BC4.
13.【解答】解:(1)∵矩形ABCD,AB=mBC,
∴,∠EDF=∠ADC=90°,
∴∠ADE=∠CDF=90°﹣∠EDC,
∵∠DAE=∠DCF=90°,
∴△ADE∽△CDF,
∴;
(2)①∵DM⊥EF,
∴∠DMG=∠FCG=90°,
∵∠DGM=∠FGC,
∴∠MDG=∠CFG,
∴,,
∴,
即,
∴,
∴,
∴;
②由(1)得,∠EDF=90°,
∴,,
∴,
∵CD∥AB,
∴△DMG∽△NME,
∴.
14.【解答】(1)证明:∵正方形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
由翻折变换的性质可知AB=AF,∠B=∠AFE=90°,
∴AF=AD,∠AFG=∠D=90°,
∵AG=AG,
∴Rt△AGD≌Rt△AGF(HL),
∴∠DAG=∠FAG;
(2)解:①由(1)可知△AGD≌△AGF,
∴GD=GF,
∵E是BC的中点,
∴BE=CE=EF=1,
设GD=GF=x,
在Rt△CGE中,EG2=CG2+EC2,
∴(1+x)2=(2﹣x)2+12,
∴x,
∴CG=2,
∴tan∠CGE;
②如图3中,连接BF,CF,BF交AE于点J,过点F作FH⊥BC于点H.
∵AB=2,BE=1,∠ABE=90°,
∴AE,
由翻折变换的性质可知,AB=AF=2,BE=EF=1,
∴AE垂直平分线段BF,
∴BJ=JF,
∵ AB BE AE BJ,
∴BJ,
∴BF,
∵∠FBC+∠ABF=90°,∠ABF+∠BAE=90°,
∴∠BAE=∠FBC,
∴tan∠FBC=tan∠BAE,
∴,
∴,
∴CF,
∵ BF CF BC FH,
∴FH,
∴CH,
∴EH=CE﹣CH=1,
∵OE∥FH∥CM,
∴.
15.【解答】(1)证明:连接DE,并延长DE,交CB的延长线于点G,
∵AD∥BC,
∴△ADE∽△BGE,
∴,
∴,即,
∵,
∴,
∵∠EDF=∠GDC,
∴△DEF∽△DGC,
∴∠DEF=∠DGC,
∴EF∥GC,即EF∥BC.
(2)解:①四边形ABMD是平行四边形;理由如下:
如图2,延长BA,CD相交于点P,
∵,
∴AB=2,BC=3,
∵AD∥BC,
∴△PAD∽△PBC,
∴,即,
∴PA=1,
∴BP=BE+AE+AP=1+1+1=3.
∵CD2=DM DN,
∴,
∵∠CDN=∠MDC,
∴△CDN∽△MDC,
∴∠DCN=∠DMC,
∵∠CEM=∠DMC,
∴∠DCN=∠CEM,
∴EM∥CD,
∴△BEM∽△BPC,
∴,即,
∴BM=1,
∴BM=AD,
∵AD∥BM,
∴四边形ABMD是平行四边形.
②延长BA,CD相交于点P,如图3,
∵△PAD∽△PBC,
∴,
∴,
∴,
∵△BEM∽△BPC,
∴,即,
∴,
∴,
∵EM∥CD,
∴△EMN∽△CDN,
∴,
设EN=a,则CN=2a,EC=EN+CN=3a,
∵∠MEC=∠NMC,∠ECM=∠MCN,
∴△ECM∽△MCN,
∴,即,
解得,
∴.
延长BA,CD相交于点P,过点E作EQ⊥BC于点Q,
设MQ=x,则BQ=BM﹣MQ=1﹣x,CQ=QM+MC=x+2,
在Rt△BEQ中,由勾股定理得:EQ2=BE2﹣BQ2,
在Rt△CEQ中,由勾股定理得:EQ2=EC2﹣CQ2,
∴BE2﹣BQ2=EC2﹣CQ2,
∴,
解得,
∴,,
在Rt△BEQ中,由勾股定理得:,
在Rt△EQM中,由勾股定理得:,
∵,
∴.
16.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=90°,
∴∠BPQ=∠A=90°,
∵△ABP与△BPQ相似,
∴或,
∵AB=6,BP=2PQ,
∴或,
∴AP=3或AP=12,
故答案为:3或12;
(2)解:过点Q作MN⊥AD于点M,与BC交于点N,
则∠A=∠PMQ=∠CNQ=90°,AB=MN=6,
∵∠BPQ=90°,
∴∠APB+∠MPQ=∠MPQ+∠PQM=90°,
∴∠APB=∠MQP,
∴△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,AP=2,
∴2,
∴x=1,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2=3,
∴CQ2=QN2+CN2=52+32=34,
∴CQ;
(3)由(2)得,△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,
∴2,
∴AP=2x,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2x=5﹣2x,
∴CQ2=QN2+CN2=(6﹣x)2+(5﹣2x)2,
=5(x)2,
当x时,CQ2的最小值为,
∴CQ长的最小值为.
17.【解答】(1)证明:如图1中,过点N作NH⊥CB交CB的延长线于点H.
∵MD=MN,∠DMN=90°,
∴△DMN是等腰直角三角形,
∴∠MDN=45°,
∵四边形ABCD是正方形,
∴CD=CB,∠C=∠ABC=90°,∠BDC=∠DBC=45°,
∵NH⊥CH,
∴∠H=∠DCM=90°,
∵∠NMH+∠DMC=90°,∠DMC+∠CDM=90°,
∴∠NMH=∠CDM,
∵MD=MN,
∴△DCM≌△MHN(AAS),
∴CD=MH=BC,CM=NH,
∴BH=CM=NH,
∴∠NBH=45°,
∴∠DBN=∠DCM=90°,
∵∠NDM=∠BDC,
∴∠NDB=∠MDC,
∴△DCM∽△DBN;
(2)解:①如图2中,过点P作PE⊥BD于点E,PF⊥BN于点F,NH⊥CB交CB的延长线于点H.
当x=1时,设CM=BM=a,则BD=2a,
由(1)可知NH=BH=CM=a,
∴BNa,
∵∠PBN=∠PBD=45°,PE⊥BD.PF⊥BN,
∴PE=PF,
∴,
∴,
∴y;
②如图3中,延长BC到T,使得CT=AP.
∵AD=CD,∠DAP=∠DCT=90°,AP=CT,
∴△DAP≌△DCT(SAS),
∴∠ADP=∠CDT,DP=DT,
∴∠PDT=∠ADC=90°,
∵∠PDM=45°,
∴∠PDM=∠TDM,
∵DM=DM,
∴△DMP≌△DMT(SAS),
∴∠DMP=∠DMT,
∵∠PMN=30°,∠DMN=90°,
∴∠DMT=∠DMP=90°﹣30°=60°,
∵CD=AB=2,
∴tan60°,
∴,
∴CM=2.
18.【解答】(1)证明:∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD为等边三角形,
∴∠ABD=60°,
∴∠G+∠BEP=60°,
∵∠FEP=60°=∠BEF+∠BEP,
∴∠BEF=∠G,
又∵∠BFE=∠EFG,
∴△EFB∽△GFE;
(2)证明:方法一:如图,过E作EM∥AD交AB于点M,则∠EMF=∠A=60°,
由(1)可知∠EBM=60°,
∴△EBM是等边三角形,
∴EM=EB,
∴EM=EB,∠MEB=60°,
∵∠FEP=60°,‘
∴∠MEF=∠BEP,
在△EMF和△EBP中,
,
∴△EMF≌△EBP(AAS),
∴EF=EP,
∴△EFP是等边三角形;
方法二:如图,过E作EM⊥AB于点M,作EN⊥BC于点N,则∠EMB=∠ENB=90°,
∵四边形ABCD是菱形,
∴BD平分∠ABC,∠ABC=120°,
∴∠EM=EN,
∵∠FEP=60°,
∴∠ABC+∠FEP=180°,
∴∠EFM+∠EPB=180°,
∵∠EPN+∠EPB=180°,
∴∠EFM=∠EPN,
在△EFM和△EPN中,
,
∴△EFM≌△EPN(AAS),
∴EF=EP,
∴△EFP是等边三角形;
(3)解:过E作EM∥AD交AB于点M,
设DE=1,FM=x,则BE=3,
∵△ABD是等边三角形,
∴AM=1,BM=3,
∴BF=3﹣x,
由(2)知△EMF≌△EBP,
∴BP=FM=x,
∵DC∥BF,
∴,
∵EF=EP,
∴,
∵∠FEP=60°,
∴∠PEQ=120°=∠PBF,
∴当△PEQ与△BFP相似时可以分两种情况讨论,
①△PEQ∽△FBP,
此时,
∴,
∴,
解得x,
由(1)知△EFB∽△GFE,
∴;
②△PEQ∽△PBF,
此时,
即,
解得x,
∴;
综上,的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
