2025年九年级中考数学三轮冲刺练习圆的证明与计算(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习圆的证明与计算(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 06:39:51 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习圆的证明与计算
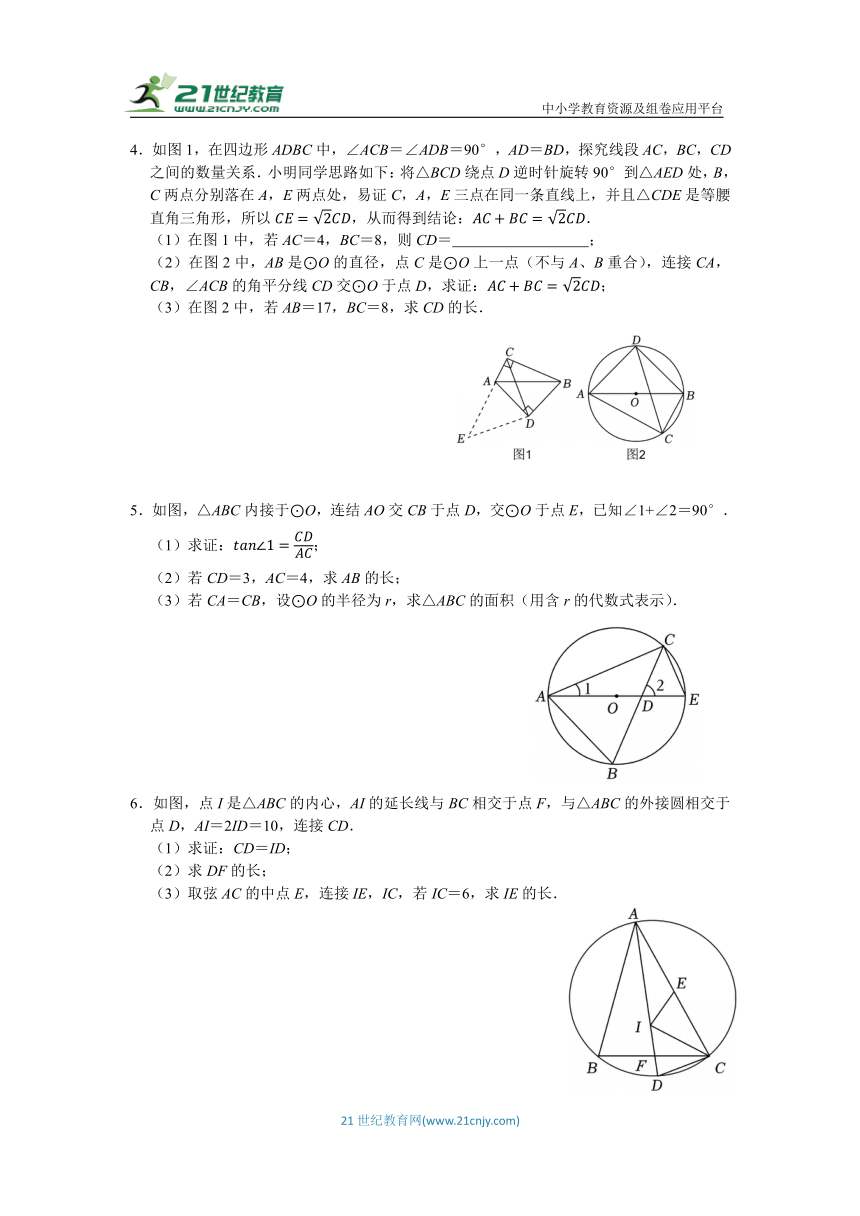
1.如图,点D在△ABC的BC边上,CD=2BD,顶点A在以CD为直径的⊙O上,过D作DE⊥BC交CA的延长线于点E,交AB于点F,FE=FA.
(1)求证:AB是⊙O的切线;
(2)若DE=2,求阴影部分面积.
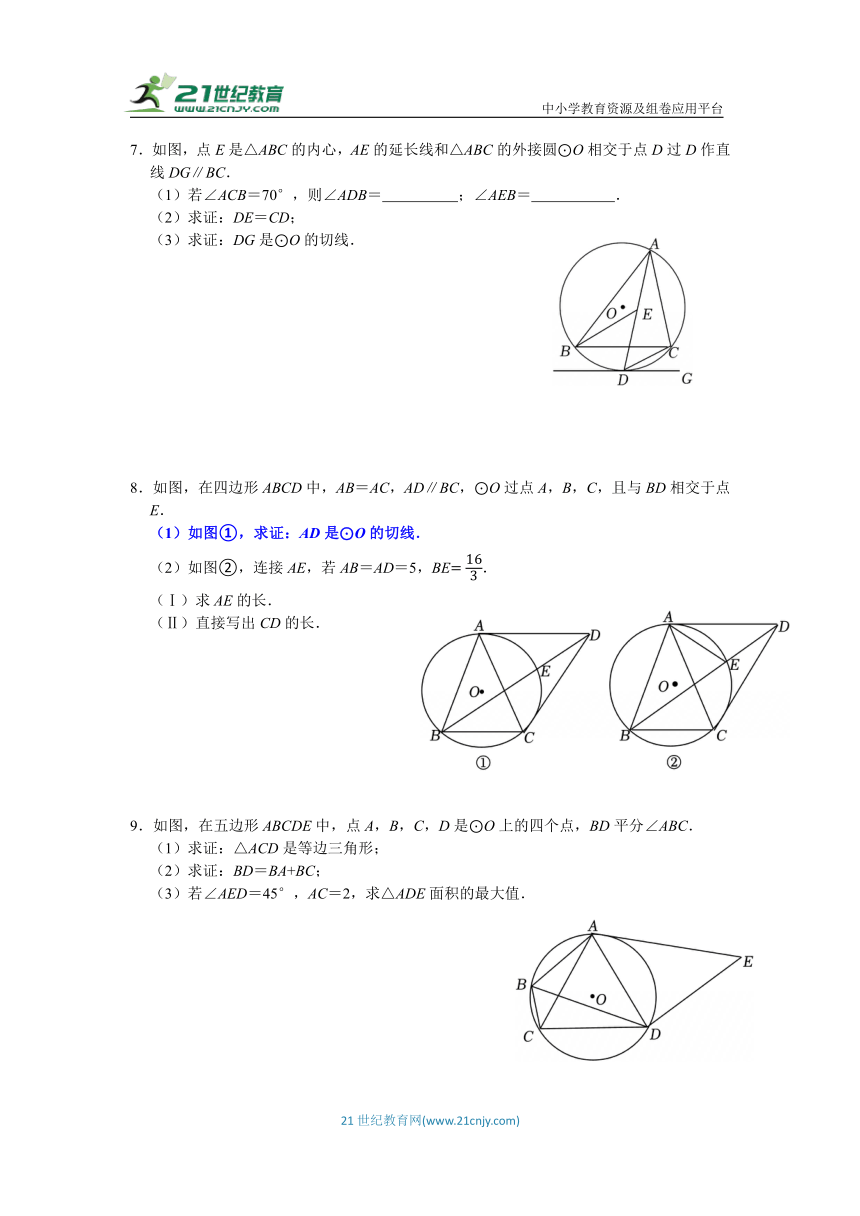
2.如图,AB为⊙O的直径,CB是⊙O的切线,切点为点B,点D为⊙O上一点,连接CD并延长交BA的延长线于点E,CD=CB.
(1)求证:CD是⊙O的切线;
(2)若AE=2,DE=4,求⊙O的半径长.
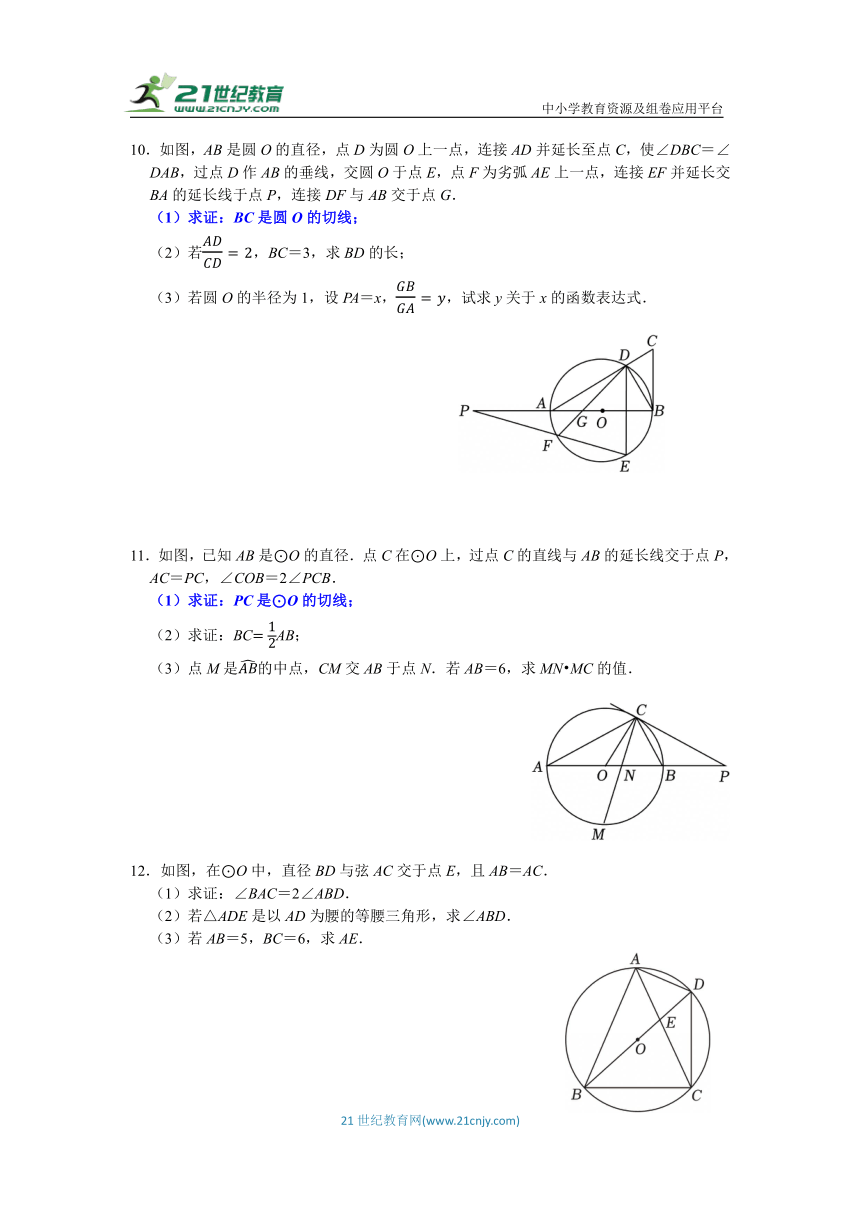
3.如图1,在⊙O中,直径AB=6,P是线段AB延长线上的一点,PC切⊙O于点C,D是⊙O上一点,切PC=PD,连接AC,BD.
(1)求证:PD是⊙O的切线;
(2)当∠CPD=90°时(如图2),求BP的长;
(3)若四边形ACPD是菱形(如图2),求弧CD与线段PC,PD围成的阴影图形的面积.
4.如图1,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.小明同学思路如下:将△BCD绕点D逆时针旋转90°到△AED处,B,C两点分别落在A,E两点处,易证C,A,E三点在同一条直线上,并且△CDE是等腰直角三角形,所以,从而得到结论:.
(1)在图1中,若AC=4,BC=8,则CD= ;
(2)在图2中,AB是⊙O的直径,点C是⊙O上一点(不与A、B重合),连接CA,CB,∠ACB的角平分线CD交⊙O于点D,求证:;
(3)在图2中,若AB=17,BC=8,求CD的长.
5.如图,△ABC内接于⊙O,连结AO交CB于点D,交⊙O于点E,已知∠1+∠2=90°.
(1)求证:;
(2)若CD=3,AC=4,求AB的长;
(3)若CA=CB,设⊙O的半径为r,求△ABC的面积(用含r的代数式表示).
6.如图,点I是△ABC的内心,AI的延长线与BC相交于点F,与△ABC的外接圆相交于点D,AI=2ID=10,连接CD.
(1)求证:CD=ID;
(2)求DF的长;
(3)取弦AC的中点E,连接IE,IC,若IC=6,求IE的长.
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D过D作直线DG∥BC.
(1)若∠ACB=70°,则∠ADB= ;∠AEB= .
(2)求证:DE=CD;
(3)求证:DG是⊙O的切线.
8.如图,在四边形ABCD中,AB=AC,AD∥BC,⊙O过点A,B,C,且与BD相交于点E.
(1)如图①,求证:AD是⊙O的切线.
(2)如图②,连接AE,若AB=AD=5,BE.
(Ⅰ)求AE的长.
(Ⅱ)直接写出CD的长.
9.如图,在五边形ABCDE中,点A,B,C,D是⊙O上的四个点,BD平分∠ABC.
(1)求证:△ACD是等边三角形;
(2)求证:BD=BA+BC;
(3)若∠AED=45°,AC=2,求△ADE面积的最大值.
10.如图,AB是圆O的直径,点D为圆O上一点,连接AD并延长至点C,使∠DBC=∠DAB,过点D作AB的垂线,交圆O于点E,点F为劣弧AE上一点,连接EF并延长交BA的延长线于点P,连接DF与AB交于点G.
(1)求证:BC是圆O的切线;
(2)若,BC=3,求BD的长;
(3)若圆O的半径为1,设PA=x,,试求y关于x的函数表达式.
11.如图,已知AB是⊙O的直径.点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BCAB;
(3)点M是的中点,CM交AB于点N.若AB=6,求MN MC的值.
12.如图,在⊙O中,直径BD与弦AC交于点E,且AB=AC.
(1)求证:∠BAC=2∠ABD.
(2)若△ADE是以AD为腰的等腰三角形,求∠ABD.
(3)若AB=5,BC=6,求AE.
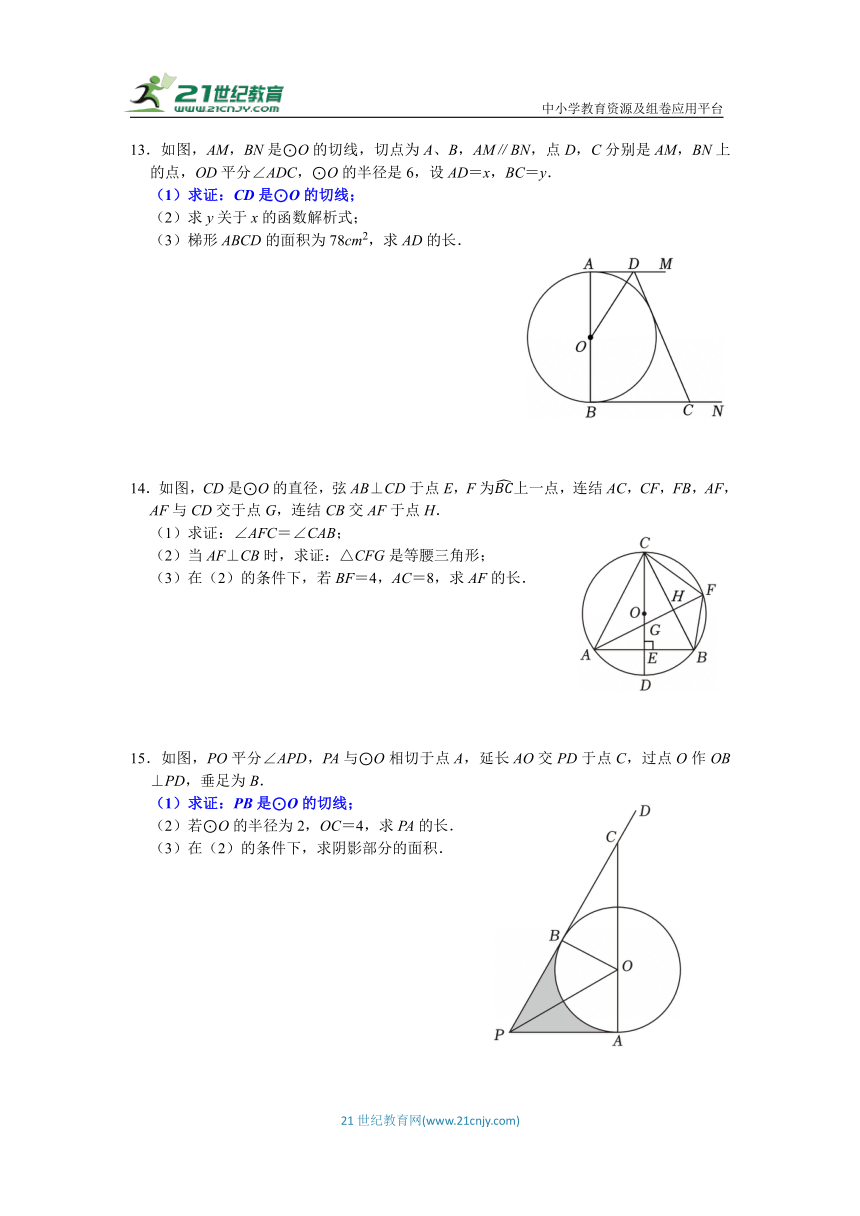
13.如图,AM,BN是⊙O的切线,切点为A、B,AM∥BN,点D,C分别是AM,BN上的点,OD平分∠ADC,⊙O的半径是6,设AD=x,BC=y.
(1)求证:CD是⊙O的切线;
(2)求y关于x的函数解析式;
(3)梯形ABCD的面积为78cm2,求AD的长.
14.如图,CD是⊙O的直径,弦AB⊥CD于点E,F为上一点,连结AC,CF,FB,AF,AF与CD交于点G,连结CB交AF于点H.
(1)求证:∠AFC=∠CAB;
(2)当AF⊥CB时,求证:△CFG是等腰三角形;
(3)在(2)的条件下,若BF=4,AC=8,求AF的长.
15.如图,PO平分∠APD,PA与⊙O相切于点A,延长AO交PD于点C,过点O作OB⊥PD,垂足为B.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,OC=4,求PA的长.
(3)在(2)的条件下,求阴影部分的面积.
16.如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,G是上的一点,连结DG交AB于点H,AG,DC的延长线交于点F.
(1)求证:∠FGC=∠AGD;
(2)①连结BD,若AG∥BD,求HE:CG的值;
②连结AD,若CG∥AD,OH=2,BE=1,求⊙O的半径r.
17.如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O分别交边AB,BC于点E,F,连结EF交CD于点K,已知BF=CF.
(1)求证:∠B=∠DCB;
(2)若,EF=2,求AC和DE的长;
(3)设,①若,求证:∠B=30°;
②设tanB=x(0<x<1),请直接写出y关于x的函数解析式.
18.如图,AB是⊙O的直径,弦AC=OA,点D在上,点E是CD中点,连结AD分别交OC,OE于点F,G.
(1)请直接写出∠AOC与∠EGD的度数.
(2)求证:△ACF∽△OGF.
(3)△AFC,△ODG的面积分别记为S1,S2.若CF=kOF,求的值.(用含k的式子表示)
参考答案
1.【解答】(1)证明:如图,连接OA,AD,
∵CD为⊙O的直径,
∴∠DAC=90°,
∴∠DAE=90°,
∴∠EAF+∠DAF=90°,∠E+∠ADE=90°.
∵FE=FA,
∴∠FAE=∠E.
∴∠DAF=∠ADE.
∵OA=OD,
∴∠OAD=∠ODA.
∵DE⊥BC,
∴∠ADF+∠ODA=90°,
∴∠OAD+∠DAF=90°,
∴∠OAF=90°,
∴OA⊥AB.
∵OA为⊙O的半径,
∴⊙O与AB相切;
(2)解:由(1)知:OA⊥AB,
∵CD=2BD,CD=2DO,
∴BD=OD,
∴ADOB=OD,
∴OD=OA=AD,
∴△OAD为等边三角形,
∴∠AOD=∠OAD=∠ODA=60°,
∴∠ADE=30°,
∵AD⊥EC,
∴AEDE=1,AD.
∴OA=OD.
过点A作AH⊥BC于点H,则DH=OH,
∴AH,
∴阴影部分面积=S△ADE﹣S弓形AD
AD AE﹣(S扇形OAD﹣S△OAD)
1 OD AH
.
2.【解答】(1)证明:连接OD,
∵AB为⊙O的直径,CB与⊙O相切于点B,
∴CB⊥AB,
∴∠B=90°,
∵CD=CB,OD=OB,
∴CD2+OD2=CB2+OB2=OC2,
∴△ODC是直角三角形,且∠ODC=90°,
∵OD是⊙O的半径,且CD⊥OD,
∴CD是⊙O的切线.
(2)解:∵∠ODE=∠B=90°,
∴DE2+OD2=OE2,
∵AE=2,DE=4,OD=OA,
∴42+OA2=(2+OA)2,
解得OA=3,
∴⊙O的半径长为3.
3.【解答】(1)证明:在⊙O中,P是线段AB延长线上的一点,如图1,连接OC、OD,则OC=OD.
在△OCP和△ODP中,
,
∴△OCP≌△ODP(SSS),
∴∠OCP=∠ODP,
∵PC切⊙O于点C,
∴∠OCP=90°,
∴∠ODP=∠OCP=90°,即PD⊥OD,
∴PD是⊙O的切线;
(2)解:在⊙O中,直径AB=6,P是线段AB延长线上的一点,PC切⊙O于点C,如图2,连接 OC、OD,由(1)可知,∠ODP=∠OCP=90°.
当∠CPD=90°时,四边形OCPD为矩形.
又∵OC=OD,
∴四边形OCPD为正方形.
∵AB=6,
∴OB=OC=3,即OD=OP=OC=3,
∴,
∴;
(3)解:在⊙O中,直径AB=6,P是线段AB延长线上的一点,PC切⊙O于点C,四边形ACPD是菱形,如图3,连接OC、OD,设∠OAC=α,则∠POC=2α,
∴∠CPO=∠OAC=α.则∠OOP=2α,
∵PC是⊙O的切线,即∠OCP=90°.
∴∠COP+∠OPC=2a+a=90°,即α=30°.
∴∠POC=2α=60°,
∴∠CPO=30°,
∵OC=3,
∴,
∴.
4.【解答】(1)解:将△BCD绕点D逆时针旋转90°到△AED处,B,C两点分别落在A,E两点处,
∴BC=EA,∠ADB=∠CDE=90°,CD=ED,∠CBD=∠EAD,
∵∠ACB=∠ADB=90°,
∴∠CBD+∠CAD=180°,
∴∠CAD+∠EAD=180°,
∴点C,A,E三点在同一条直线上,
∴△CDE是等腰直角三角形,
∴CECD,
∵CE=AC+EA=AC+BC,
∴AC+BCCD,
∵AC=4,BC=8,
∴CD=12,
∴CD=6,
故答案为:6;
(2)证明:∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴AD=BD,
如图,将△DAC绕点D逆时针旋转90°到△DBF处,A,C两点分别落在B,F两点处,
∴CD=FD,∠CDF=90°,AC=BF,CD=DF,
∵90°=∠ACB=∠ADB,
∴180°=∠CBD+∠CAD,
∴180°=∠FBD+∠DBC,
∴点C,B,F三点在同一条直线上,
∴△CDF是等腰直角三角形,
∴CFCD,
∵CE=AC+BC=AC+EA,
∴AC+BCCD;
(3)解:由(2)得:AC+BCCD,∠ACB=90°,
∴AC15,
∴18+8CD,
∴CD.
5.【解答】(1)证明:如图1,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴∠1+∠AEC=90°,
∵∠1+∠2=90°,
∴∠AEC=∠2,
∴CD=CE,
∵tan∠1,
∴;
(2)解:如图2,过点C作CM⊥AE于M,
∵CD=CE=3,AC=4,∠ACE=90°,
∴AE5,
∴S△ABE3×45CM,
∴CM,
由勾股定理得:EM,
∵CD=CE,CM⊥DE,
∴DE=2EM,
∴AD=5,
∵∠ADB=∠2,∠B=∠E,∠2=∠E,
∴∠ADB=∠B,
∴AB=AD;
(3)解:如图3,连接CO并延长交AB于F,连接OB,
∵CA=CB,
∴,∠CAB=∠CBA,
∴CF⊥AB,
∴∠AFO=∠BFO=90°,AF=BF,
由(2)知:∠2=∠E=∠ADB=∠CBA,
∴∠DCE=∠ACB,
∴,
∴∠AOB=∠EOB=90°,
∵OA=OB,
∴△AOB是等腰直角三角形,
∴∠OAB=∠OBA=45°,
在Rt△AOB中,AF=BF,
∴OFAB=AF=BF,
设AF=a,则OF=a,
∵OA2=AF2+OF2,
∴r2=a2+a2,
∴ra,
∵S△ABC AB CF,
∴S△ABC 2a(a+r)=a2+ay.
6.【解答】解:(1)∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠BCI=∠ACI,
∵∠BAD=∠BCD,
∴∠CAD=∠BCD,
又∵∠DIC=∠CAD+∠ACI,∠DCI=∠BCD+∠BCI,
∴∠DIC=∠DCI,
∴CD=ID.
(2)∵AI=2ID=10,
∴AD=15,ID=5,
∵∠D=∠D,∠BCD=∠DAC,
∴△DCF∽△DAC,
∴,即CD2=DF AD
∴52=DF×15,解得:.
(3)延长ID到M,使得DM=ID,连接CM,
∵DI=DC,
∴DI=DC=DM,
∴点I,C,M在以点D为圆心,5为半径的圆上,
∴IM是直径,
∴∠ICM=90°,
∴,
∵AI=2ID=10,AE=EC,
∴AI=IM,.
7.【解答】(1)解:如图,连接BD,OD,
∵,
∴∠ACB=∠ADB=70°,
∴∠ABC+∠BAC=110°,
∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE,
∴∠BAE+∠ABE=55°,
∴∠AEB=125°,
故答案为:70°,125°;
(2)证明:∵∠BAE=∠CAE,
∴,
∴BD=CD,
∵∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BED=∠BAE+∠ABE=∠CBD+∠CBE=∠DBE,
∴BD=DE,
∴DE=CD;
(3)证明:∵,
∴OD⊥BC,
∵DG∥BC,
∴OD⊥DG,
又∵OD是半径,
∴DG是⊙O的切线.
8.【解答】(1)证明:如图①,连接AO,并延长交⊙O于T,交BC于K,
∵AB=AC,
∴,
∴AO⊥BC,
∵AD∥BC,
∴AO⊥AD,
∴AD是⊙O的切线;
(2)解:(I)如图②,连接AO,并延长交⊙O于T,连接TE,
∴∠ABD=∠T,
∵AT为直径,
∴∠AET=90°=∠TAD,
∴∠T=90°﹣∠TAE=∠DAE,
∴∠DAE=∠ABD,
∵∠ADE=∠BDA,
∴△DAE∽△DBA,
∴,
∵,
∴,
解得:DE=3(负根舍去),
∴AE=DE=3;
(II)连接AO,并延长交⊙O于T,连接TE,过A作AN⊥BD于N,过C作CM⊥AD于M,如图③,
由(1)得:AK⊥BC,AK⊥AD,
∴四边形AKCM为矩形,
∴AM=CK,AK=CM,
∵AB=AD=5,,
∴,,
在直角三角形ABN中,由勾股定理得:,
∵AE=DE=3,∠AKC=∠ANE=90°,AB=AC=AD=5,
∴,
∴,
∴,
在直角三角形ACK中,由勾股定理得:,
∴,
∴.
9.【解答】(1)证明:∵∠ABC=120°,BD平分∠ABC,
∴∠ABD=∠CBD∠ABC=60°,
∵,,
∴∠ACD=∠ABD=60°,∠CAD=∠CBD=60°,
∴∠ACD=∠CAD=60°,
∴∠ADC=180°﹣∠ACD﹣∠CAD=60°,
∴∠ADC=∠ACD=∠CAD=60°,
∴△ACD是等边三角形;
(2)证明:延长AB至F,使BF=BC,如图1,
∴△BCF是等腰三角形,
∵∠CBF=180°﹣∠ABD﹣∠CBD=60°,
∴△BCF是等边三角形,
∴CF=CB,∠FCB=60°,
由(1)知,CA=CD,∠ACD=60°,
∴∠FCB+∠BCA=∠ACD+∠BCA,
即∠FCA=∠BCD,
在△FCA和△BCD中,
,
∴△FCA≌△BCD(SAS),
∴FA=BD,
∵FA=AB+BF=AB+BC,
∴BD=AB+BC;
(3)解:设△ADE的外心为M,连接AM,DM,
∴AM=MD,
∵∠AED=45°,
∴∠AMD=90°,
∴点M为定点,
∵AD=AC=2,
∴点E在以M为圆心,AM为半径的圆上,如图2,
在等腰直角三角形ADM中,MN⊥AD于点N,MN=1,
当点E,M,N三点共线时,△ADE的面积最大,
∴ME=MD,
∴EN=ME+MN,
∴S△ADEAD EN1.
10.【解答】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵∠DBC=∠DAB,
∴∠ABD+∠DBC=90°,
∴∠ABC=90°,
又∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)解:设CD=a,
∵,
∴AD=2a,
∴AC=3a,
∵∠DBC=∠DAB,∠BCD=∠ACB,
∴△BCD∽△ACB,
∴,即,
解得(负值已舍),
∴,
∵∠CDB=180°﹣∠ADB=90°,
∴;
(3)解:如图,连接OD,OE,AE,BF,
∵∠PEA=∠PBF,∠P=∠P,
∴△PAE∽△PFB,
∴,
∴PE PF=PA PB,
∵DE⊥AB,且AB为⊙O的直径,
∴,
∵,
∴∠BOE=∠DFE,
∵∠PFG+∠DFE=180°,∠POE+∠BOE=180°,
∴∠POE=∠PFG,
∵∠P=∠P,
∴△PEO∽△PGF,
∴,
∴PE PF=PO PG,
∴PA PB=PO PG,
设AG=m,则PG=x+m,
∴x(x+2)=(x+1)(x+m),
∴,
∴.
11.【解答】(1)证明:∵OA=OC,
∴∠A=∠ACO,
又∵∠COB=A+∠ACO=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB,
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线;
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P,
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC,
∴;
(3)解:连接MA,MB,
∵点M是的中点,
∴,
∴∠ACM=∠BCM,
∵∠ACM=∠ABM,
∴∠BCM=∠ABM,
∵∠BMN=∠BMC,
∴△MBN∽△MCB,
∴,
∴BM2=MN MC,
又∵AB是⊙O的直径,,
∴∠AMB=90°,AM=BM,
∵AB=6,
∴,
∴.
12.【解答】(1)证明:连接OA并延长交BC于H点,如图,
∵AB=AC,
∴,
∴AH垂直平分BC,
∴AH平分∠BAC,
即∠BAC=2∠BAH,
∵OA=OB,
∴∠ABD=∠BAH,
∴∠BAC=2∠ABD;
(2)解:设∠ABD=α,则∠BAC=2α,
∴∠AED=∠ABD+∠BAC=α+2α=3α,
∵AB为直径,
∴∠BAD=90°,
当AD=AE时,∠ADB=∠AED=3α,
∴α+3α=90°,
解得α=22.5°;
当DA=DE时,∠DAE=∠AED=3α,
∴2α+3α=90°,
解得α=18°,
综上所述,∠ABD的度数为18°或22.5°;
(3)解:∵AH⊥BC,
∴BH=CHBC=3,
在Rt△ABH中,AH4,
设⊙O的半径为r,则OA=OB=r,OH=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,
解得r,
∴BD=2r,
在Rt△ABD中,AD,
在Rt△BCD中,CD,
∵AH∥CD,
∴△AEO∽△CED,
∴,
∴,
∴AE5.
13.【解答】(1)证明:,AM,BN是⊙O的切线,OD平分∠ADC,如图1,过点O作OE⊥CD于点E,则∠OED=90°,
∴∠OAD=90°,∠ADO=∠EDO,
在△OAD和△OED中,
,
∴△OAD≌△OED(AAS),
∴OA=OE,
∵OA是⊙O的半径,
∴OE是⊙O的半径,
∴CD是⊙O的切线;
(2)解:AM,BN,CD是⊙O的切线,⊙O的半径是6,如图2,过点D作DF⊥BC于点F,
∴∠MAO=∠NBO=90°,
∴四边形ABFD是矩形,
∴DF=AB=2r=12,
由切线长定理得:AD=DE,CB=CE,
∵AD=x,BC=y,
∴CF=BC﹣BF=y﹣x,CD=x+y,
在Rt△DCF中,CD2=DF2+CF2,即(x+y)2=122+(y﹣x)2,
化简得;
(3)解:∵梯形ABCD是直角梯形,则cm2,
设AD=x,由(2)可知,
∴,
化简得x2﹣13x+36=0,
解得x=4或x=9,
∴AD长为4cm或9cm.
14.【解答】(1)证明:∵弦AB⊥直径CD,
∴,
∴∠AFC=∠CAB;
(2)证明:如图1,
△CFG是等腰三角形,理由如下:
设AF,BC交于点H,
∵AF⊥BC,
∴∠CHF=90°,
∴∠BCF+∠AFC=90°,
∵CD⊥AB,
∴∠CEB=90°,
∴∠B+∠BCD=90°,
∵,
∴∠ABC=∠AFC,
∴∠BCD=∠BCF,
∴∠CGH=∠AFC,
∴CG=CF,
∴△CFG是等腰三角形;
(3)解:如图2,
连接BG,AD,
由(2)知,
CG=CF,AF⊥BC,∠BCF=∠BAF,
∴CH=FH,∠BDC=∠BCF,
∴BG=BF=4,
∵CD⊥AB,
∴AE=BE,∠DAC=∠BCD,
∴AG=BG=4,∠BAF=∠ACD,
∴∠AEG=∠AEC,
∴△AEG∽△CEA,
∴,
∵AE2+EG2=AG2,
∴(2EG)2+EG2=42,
∴EG,
∴BE=AE=2EG,
∴CE=2AE,
∴CG=CE﹣EG,
∵,
∴∠BAD=∠BCD,
∵∠AED=∠BEC,
∴△AED=∠BEC,
∴△AED∽△CEB,
∴,
∴DE CE=AE BE,
DE,
∴DE,
∴DG=DE+EG,
同理可得,
AG FG=DG CG,
∴4FG,
∴FG,
∴AF=AG+FG.
15.【解答】(1)证明:∵PA与⊙O相切于点A,
∴OA⊥PA,
∵PO平分∠APD,OB⊥PD,
∴OA=OB,
∴OB是圆的半径,
∴PB是⊙O的切线;
(2)解:∵⊙O的半径为2,
∴OA=OB=2,
∵OB⊥PD,OC=4,
∴,AC=OA+OC=2+4=6,
∵PA,PB都是⊙O的切线,
∴设PA=PB=x,则,
∴在Rt△PAC中,PA2+AC2=PC2,
∴,
解得,
∴;
(3)在Rt△BCO中,∠CBO=90°,OC=2OB,
∴∠BCO=30°,∠BOC=60°,
∴∠BOA=120°,
∴,
,,
∴.
16.【解答】(1))证明:连接AD,如图,
∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴∠ADC=∠AGD,
∵四边形AGCD为圆的内接四边形,
∴∠FGC=∠ADC.
∴∠FGC=∠AGD;
(2)解:①连接OG,如图,
∵OA=OG,
∴∠A=∠OGA,
∵AG∥BD,
∴∠B=∠A,
∵∠B=∠AGD,
∴∠A=∠AGD,
∴∠AGD=∠OGA,
∴DG经过点O,
∴O,H重合,即DG为圆的直径,
∴∠GCD=90°,
∴CG⊥DC,
∵CD⊥AB,
∴HE∥GC,
∴△DHE∽△DCG,
∴;
②连接BD,AC,如图,
∵⊙O的半径r,OH=2,BE=1,
∴BH=r﹣2,AH=r+2,HE=r﹣3,AE=2r﹣1,
∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴AD=AC.
∵CG∥AD,
∴,
∴,
∴AC=DG,
∴AD=DG.
∵AB是⊙O的直径,
∴∠ADB=90°,
∵CD⊥AB,
∴△BDE∽△EAD,
∴,
∴DE2=BE AE=1×(2r﹣1)=2r﹣1,
∴ADDG,
∵DH2=DE2+HE2,
∴DH,
∴HG=DG﹣DH.
∵∠DHB=∠GHA,∠AGD=∠DBA,
∴△BDH∽△GAH,
∴,
∴,
∴r3﹣4r2﹣8r+8=0,
∴(r+2)(r2﹣6r+4)=0,
∵r>0,
∴r2﹣6r+4=0,
∴r=3±,
∵由题意:r>3,
∴r=3.
∴⊙O的半径为3.
17.【解答】(1)证明:如图1,连接DF,
∵DC为⊙O的直径,
∴∠DFC=90°,
∴DF⊥BC,
∵BF=CF,
∴DF是BC的垂直平分线,
∴BD=CD,
∴∠B=∠DCB;
(2)解:如图2,连接DF,CE,过点E作EM⊥BC于M,
∵,
∴设DF=3x,BF=4x,
∴BD=CD=5x,
∵∠ACB=90°,
∴∠A+∠B=∠ACD+∠DCB=90°,
∴∠A=∠ACD,
∴AD=CD=5x,
∵DC为⊙O的直径,
∴∠DEC=90°,
由勾股定理得:AC6x,
∵S△ABC AC BC AB CE,
∴ 6x 8x 10x CE,
∴CE=4.8x,
∴DE1.4x,
∵EM⊥BC,AC⊥BC,
∴EM∥AC,
∴△BEM∽△BAC,
∴,
∴,
∴BM=5.12x,EM=3.84x,
∴FM=5.12x﹣4x=1.12x,
在Rt△EFM中,EF2=EM2+FM2,
∴22=(3.84x)2+(1.12x)2,
∴x(负值舍),
∴AC=6x=63,DE=1.4x=1.40.7;
(3)①证明:如图3,延长CA,FE交于点P,连接DG,CE,DF,
∵DE是⊙O的直径,
∴∠DEC=∠DGC=90°,
∴DG⊥AC,
由(1)知:AD=CD=BD,
∴AG=CG,
∵∠DFC=∠DGC=∠FCG=90°,
∴四边形DFCG是矩形,
∴DF=CG,DF∥AC,
∴△DKF∽△CKP,∠P=∠DFE,
∴,
∴CP=3DF,
∴AP=DF,
∵∠DEF=∠PEA,
∴△DEF≌△AEP(AAS),
∴DE=AE,
∴CE是AD的垂直平分线,
∴AC=CD=AD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴∠DCB=90°﹣60°=30°,
∴∠B=30°;
②解:如图4,延长CA,FE交于点P,连接DF,CE,
∵∠BFD=∠BCA=90°,
∴DF∥AC,
∴△BDF∽△BAC,△DFK∽△CPK,
∴,y,
∴AC=2DF,DF=CP y,
∵tanBx,
∴DF=BF x,
设BF=m,则DF=mx,AC=2mx,
∴y,
由勾股定理得:DCm,
∵∠AEC=∠DFC,∠ACE=∠B=∠DCB,
∴△AEC∽△DFC,
∴,
∴AE,
∴DE=AD﹣AE=CD﹣AE=m,
∵DF∥AP,
∴△DEF∽△AEP,
∴,
∴,
∴AP,
∴y.
18.【解答】(1)解:∵AC=OA,OA=OC,
∴OA=OC=AC,
∴△OAC为等边三角形,
∴∠AOC=∠ACF=60°,
∴,
∵点E是CD中点,OE经过圆心,
∴OE⊥CD,
∴∠EGD=90°﹣∠ADC=60°;
(2)证明:∵∠EGD=60°,
∴∠FGO=∠EGD=60°,
∵∠ACF=60°,
∴∠ACF=∠OGF,
∵∠AFC=∠OFG,
∴△ACF∽△OGF;
(3)解:过点C作CM⊥AD于点M,过点F作FH⊥AO于点H,
由CF=kOF,不妨设OF=1,则CF=k,
∴AC=AO=OC=k+1,
∵∠AOC=60°,
∴,,
∴,
∴在Rt△AFH中,由勾股定理得,,
∵△ACF﹣△OGF,
∴,
∴,
∴,
∵∠CDA=30°,
∴在Rt△CMD 中,,
∴,,
∴.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习圆的证明与计算
1.如图,点D在△ABC的BC边上,CD=2BD,顶点A在以CD为直径的⊙O上,过D作DE⊥BC交CA的延长线于点E,交AB于点F,FE=FA.
(1)求证:AB是⊙O的切线;
(2)若DE=2,求阴影部分面积.
2.如图,AB为⊙O的直径,CB是⊙O的切线,切点为点B,点D为⊙O上一点,连接CD并延长交BA的延长线于点E,CD=CB.
(1)求证:CD是⊙O的切线;
(2)若AE=2,DE=4,求⊙O的半径长.
3.如图1,在⊙O中,直径AB=6,P是线段AB延长线上的一点,PC切⊙O于点C,D是⊙O上一点,切PC=PD,连接AC,BD.
(1)求证:PD是⊙O的切线;
(2)当∠CPD=90°时(如图2),求BP的长;
(3)若四边形ACPD是菱形(如图2),求弧CD与线段PC,PD围成的阴影图形的面积.
4.如图1,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.小明同学思路如下:将△BCD绕点D逆时针旋转90°到△AED处,B,C两点分别落在A,E两点处,易证C,A,E三点在同一条直线上,并且△CDE是等腰直角三角形,所以,从而得到结论:.
(1)在图1中,若AC=4,BC=8,则CD= ;
(2)在图2中,AB是⊙O的直径,点C是⊙O上一点(不与A、B重合),连接CA,CB,∠ACB的角平分线CD交⊙O于点D,求证:;
(3)在图2中,若AB=17,BC=8,求CD的长.
5.如图,△ABC内接于⊙O,连结AO交CB于点D,交⊙O于点E,已知∠1+∠2=90°.
(1)求证:;
(2)若CD=3,AC=4,求AB的长;
(3)若CA=CB,设⊙O的半径为r,求△ABC的面积(用含r的代数式表示).
6.如图,点I是△ABC的内心,AI的延长线与BC相交于点F,与△ABC的外接圆相交于点D,AI=2ID=10,连接CD.
(1)求证:CD=ID;
(2)求DF的长;
(3)取弦AC的中点E,连接IE,IC,若IC=6,求IE的长.
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D过D作直线DG∥BC.
(1)若∠ACB=70°,则∠ADB= ;∠AEB= .
(2)求证:DE=CD;
(3)求证:DG是⊙O的切线.
8.如图,在四边形ABCD中,AB=AC,AD∥BC,⊙O过点A,B,C,且与BD相交于点E.
(1)如图①,求证:AD是⊙O的切线.
(2)如图②,连接AE,若AB=AD=5,BE.
(Ⅰ)求AE的长.
(Ⅱ)直接写出CD的长.
9.如图,在五边形ABCDE中,点A,B,C,D是⊙O上的四个点,BD平分∠ABC.
(1)求证:△ACD是等边三角形;
(2)求证:BD=BA+BC;
(3)若∠AED=45°,AC=2,求△ADE面积的最大值.
10.如图,AB是圆O的直径,点D为圆O上一点,连接AD并延长至点C,使∠DBC=∠DAB,过点D作AB的垂线,交圆O于点E,点F为劣弧AE上一点,连接EF并延长交BA的延长线于点P,连接DF与AB交于点G.
(1)求证:BC是圆O的切线;
(2)若,BC=3,求BD的长;
(3)若圆O的半径为1,设PA=x,,试求y关于x的函数表达式.
11.如图,已知AB是⊙O的直径.点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BCAB;
(3)点M是的中点,CM交AB于点N.若AB=6,求MN MC的值.
12.如图,在⊙O中,直径BD与弦AC交于点E,且AB=AC.
(1)求证:∠BAC=2∠ABD.
(2)若△ADE是以AD为腰的等腰三角形,求∠ABD.
(3)若AB=5,BC=6,求AE.
13.如图,AM,BN是⊙O的切线,切点为A、B,AM∥BN,点D,C分别是AM,BN上的点,OD平分∠ADC,⊙O的半径是6,设AD=x,BC=y.
(1)求证:CD是⊙O的切线;
(2)求y关于x的函数解析式;
(3)梯形ABCD的面积为78cm2,求AD的长.
14.如图,CD是⊙O的直径,弦AB⊥CD于点E,F为上一点,连结AC,CF,FB,AF,AF与CD交于点G,连结CB交AF于点H.
(1)求证:∠AFC=∠CAB;
(2)当AF⊥CB时,求证:△CFG是等腰三角形;
(3)在(2)的条件下,若BF=4,AC=8,求AF的长.
15.如图,PO平分∠APD,PA与⊙O相切于点A,延长AO交PD于点C,过点O作OB⊥PD,垂足为B.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,OC=4,求PA的长.
(3)在(2)的条件下,求阴影部分的面积.
16.如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,G是上的一点,连结DG交AB于点H,AG,DC的延长线交于点F.
(1)求证:∠FGC=∠AGD;
(2)①连结BD,若AG∥BD,求HE:CG的值;
②连结AD,若CG∥AD,OH=2,BE=1,求⊙O的半径r.
17.如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O分别交边AB,BC于点E,F,连结EF交CD于点K,已知BF=CF.
(1)求证:∠B=∠DCB;
(2)若,EF=2,求AC和DE的长;
(3)设,①若,求证:∠B=30°;
②设tanB=x(0<x<1),请直接写出y关于x的函数解析式.
18.如图,AB是⊙O的直径,弦AC=OA,点D在上,点E是CD中点,连结AD分别交OC,OE于点F,G.
(1)请直接写出∠AOC与∠EGD的度数.
(2)求证:△ACF∽△OGF.
(3)△AFC,△ODG的面积分别记为S1,S2.若CF=kOF,求的值.(用含k的式子表示)
参考答案
1.【解答】(1)证明:如图,连接OA,AD,
∵CD为⊙O的直径,
∴∠DAC=90°,
∴∠DAE=90°,
∴∠EAF+∠DAF=90°,∠E+∠ADE=90°.
∵FE=FA,
∴∠FAE=∠E.
∴∠DAF=∠ADE.
∵OA=OD,
∴∠OAD=∠ODA.
∵DE⊥BC,
∴∠ADF+∠ODA=90°,
∴∠OAD+∠DAF=90°,
∴∠OAF=90°,
∴OA⊥AB.
∵OA为⊙O的半径,
∴⊙O与AB相切;
(2)解:由(1)知:OA⊥AB,
∵CD=2BD,CD=2DO,
∴BD=OD,
∴ADOB=OD,
∴OD=OA=AD,
∴△OAD为等边三角形,
∴∠AOD=∠OAD=∠ODA=60°,
∴∠ADE=30°,
∵AD⊥EC,
∴AEDE=1,AD.
∴OA=OD.
过点A作AH⊥BC于点H,则DH=OH,
∴AH,
∴阴影部分面积=S△ADE﹣S弓形AD
AD AE﹣(S扇形OAD﹣S△OAD)
1 OD AH
.
2.【解答】(1)证明:连接OD,
∵AB为⊙O的直径,CB与⊙O相切于点B,
∴CB⊥AB,
∴∠B=90°,
∵CD=CB,OD=OB,
∴CD2+OD2=CB2+OB2=OC2,
∴△ODC是直角三角形,且∠ODC=90°,
∵OD是⊙O的半径,且CD⊥OD,
∴CD是⊙O的切线.
(2)解:∵∠ODE=∠B=90°,
∴DE2+OD2=OE2,
∵AE=2,DE=4,OD=OA,
∴42+OA2=(2+OA)2,
解得OA=3,
∴⊙O的半径长为3.
3.【解答】(1)证明:在⊙O中,P是线段AB延长线上的一点,如图1,连接OC、OD,则OC=OD.
在△OCP和△ODP中,
,
∴△OCP≌△ODP(SSS),
∴∠OCP=∠ODP,
∵PC切⊙O于点C,
∴∠OCP=90°,
∴∠ODP=∠OCP=90°,即PD⊥OD,
∴PD是⊙O的切线;
(2)解:在⊙O中,直径AB=6,P是线段AB延长线上的一点,PC切⊙O于点C,如图2,连接 OC、OD,由(1)可知,∠ODP=∠OCP=90°.
当∠CPD=90°时,四边形OCPD为矩形.
又∵OC=OD,
∴四边形OCPD为正方形.
∵AB=6,
∴OB=OC=3,即OD=OP=OC=3,
∴,
∴;
(3)解:在⊙O中,直径AB=6,P是线段AB延长线上的一点,PC切⊙O于点C,四边形ACPD是菱形,如图3,连接OC、OD,设∠OAC=α,则∠POC=2α,
∴∠CPO=∠OAC=α.则∠OOP=2α,
∵PC是⊙O的切线,即∠OCP=90°.
∴∠COP+∠OPC=2a+a=90°,即α=30°.
∴∠POC=2α=60°,
∴∠CPO=30°,
∵OC=3,
∴,
∴.
4.【解答】(1)解:将△BCD绕点D逆时针旋转90°到△AED处,B,C两点分别落在A,E两点处,
∴BC=EA,∠ADB=∠CDE=90°,CD=ED,∠CBD=∠EAD,
∵∠ACB=∠ADB=90°,
∴∠CBD+∠CAD=180°,
∴∠CAD+∠EAD=180°,
∴点C,A,E三点在同一条直线上,
∴△CDE是等腰直角三角形,
∴CECD,
∵CE=AC+EA=AC+BC,
∴AC+BCCD,
∵AC=4,BC=8,
∴CD=12,
∴CD=6,
故答案为:6;
(2)证明:∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴AD=BD,
如图,将△DAC绕点D逆时针旋转90°到△DBF处,A,C两点分别落在B,F两点处,
∴CD=FD,∠CDF=90°,AC=BF,CD=DF,
∵90°=∠ACB=∠ADB,
∴180°=∠CBD+∠CAD,
∴180°=∠FBD+∠DBC,
∴点C,B,F三点在同一条直线上,
∴△CDF是等腰直角三角形,
∴CFCD,
∵CE=AC+BC=AC+EA,
∴AC+BCCD;
(3)解:由(2)得:AC+BCCD,∠ACB=90°,
∴AC15,
∴18+8CD,
∴CD.
5.【解答】(1)证明:如图1,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴∠1+∠AEC=90°,
∵∠1+∠2=90°,
∴∠AEC=∠2,
∴CD=CE,
∵tan∠1,
∴;
(2)解:如图2,过点C作CM⊥AE于M,
∵CD=CE=3,AC=4,∠ACE=90°,
∴AE5,
∴S△ABE3×45CM,
∴CM,
由勾股定理得:EM,
∵CD=CE,CM⊥DE,
∴DE=2EM,
∴AD=5,
∵∠ADB=∠2,∠B=∠E,∠2=∠E,
∴∠ADB=∠B,
∴AB=AD;
(3)解:如图3,连接CO并延长交AB于F,连接OB,
∵CA=CB,
∴,∠CAB=∠CBA,
∴CF⊥AB,
∴∠AFO=∠BFO=90°,AF=BF,
由(2)知:∠2=∠E=∠ADB=∠CBA,
∴∠DCE=∠ACB,
∴,
∴∠AOB=∠EOB=90°,
∵OA=OB,
∴△AOB是等腰直角三角形,
∴∠OAB=∠OBA=45°,
在Rt△AOB中,AF=BF,
∴OFAB=AF=BF,
设AF=a,则OF=a,
∵OA2=AF2+OF2,
∴r2=a2+a2,
∴ra,
∵S△ABC AB CF,
∴S△ABC 2a(a+r)=a2+ay.
6.【解答】解:(1)∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠BCI=∠ACI,
∵∠BAD=∠BCD,
∴∠CAD=∠BCD,
又∵∠DIC=∠CAD+∠ACI,∠DCI=∠BCD+∠BCI,
∴∠DIC=∠DCI,
∴CD=ID.
(2)∵AI=2ID=10,
∴AD=15,ID=5,
∵∠D=∠D,∠BCD=∠DAC,
∴△DCF∽△DAC,
∴,即CD2=DF AD
∴52=DF×15,解得:.
(3)延长ID到M,使得DM=ID,连接CM,
∵DI=DC,
∴DI=DC=DM,
∴点I,C,M在以点D为圆心,5为半径的圆上,
∴IM是直径,
∴∠ICM=90°,
∴,
∵AI=2ID=10,AE=EC,
∴AI=IM,.
7.【解答】(1)解:如图,连接BD,OD,
∵,
∴∠ACB=∠ADB=70°,
∴∠ABC+∠BAC=110°,
∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE,
∴∠BAE+∠ABE=55°,
∴∠AEB=125°,
故答案为:70°,125°;
(2)证明:∵∠BAE=∠CAE,
∴,
∴BD=CD,
∵∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BED=∠BAE+∠ABE=∠CBD+∠CBE=∠DBE,
∴BD=DE,
∴DE=CD;
(3)证明:∵,
∴OD⊥BC,
∵DG∥BC,
∴OD⊥DG,
又∵OD是半径,
∴DG是⊙O的切线.
8.【解答】(1)证明:如图①,连接AO,并延长交⊙O于T,交BC于K,
∵AB=AC,
∴,
∴AO⊥BC,
∵AD∥BC,
∴AO⊥AD,
∴AD是⊙O的切线;
(2)解:(I)如图②,连接AO,并延长交⊙O于T,连接TE,
∴∠ABD=∠T,
∵AT为直径,
∴∠AET=90°=∠TAD,
∴∠T=90°﹣∠TAE=∠DAE,
∴∠DAE=∠ABD,
∵∠ADE=∠BDA,
∴△DAE∽△DBA,
∴,
∵,
∴,
解得:DE=3(负根舍去),
∴AE=DE=3;
(II)连接AO,并延长交⊙O于T,连接TE,过A作AN⊥BD于N,过C作CM⊥AD于M,如图③,
由(1)得:AK⊥BC,AK⊥AD,
∴四边形AKCM为矩形,
∴AM=CK,AK=CM,
∵AB=AD=5,,
∴,,
在直角三角形ABN中,由勾股定理得:,
∵AE=DE=3,∠AKC=∠ANE=90°,AB=AC=AD=5,
∴,
∴,
∴,
在直角三角形ACK中,由勾股定理得:,
∴,
∴.
9.【解答】(1)证明:∵∠ABC=120°,BD平分∠ABC,
∴∠ABD=∠CBD∠ABC=60°,
∵,,
∴∠ACD=∠ABD=60°,∠CAD=∠CBD=60°,
∴∠ACD=∠CAD=60°,
∴∠ADC=180°﹣∠ACD﹣∠CAD=60°,
∴∠ADC=∠ACD=∠CAD=60°,
∴△ACD是等边三角形;
(2)证明:延长AB至F,使BF=BC,如图1,
∴△BCF是等腰三角形,
∵∠CBF=180°﹣∠ABD﹣∠CBD=60°,
∴△BCF是等边三角形,
∴CF=CB,∠FCB=60°,
由(1)知,CA=CD,∠ACD=60°,
∴∠FCB+∠BCA=∠ACD+∠BCA,
即∠FCA=∠BCD,
在△FCA和△BCD中,
,
∴△FCA≌△BCD(SAS),
∴FA=BD,
∵FA=AB+BF=AB+BC,
∴BD=AB+BC;
(3)解:设△ADE的外心为M,连接AM,DM,
∴AM=MD,
∵∠AED=45°,
∴∠AMD=90°,
∴点M为定点,
∵AD=AC=2,
∴点E在以M为圆心,AM为半径的圆上,如图2,
在等腰直角三角形ADM中,MN⊥AD于点N,MN=1,
当点E,M,N三点共线时,△ADE的面积最大,
∴ME=MD,
∴EN=ME+MN,
∴S△ADEAD EN1.
10.【解答】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵∠DBC=∠DAB,
∴∠ABD+∠DBC=90°,
∴∠ABC=90°,
又∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)解:设CD=a,
∵,
∴AD=2a,
∴AC=3a,
∵∠DBC=∠DAB,∠BCD=∠ACB,
∴△BCD∽△ACB,
∴,即,
解得(负值已舍),
∴,
∵∠CDB=180°﹣∠ADB=90°,
∴;
(3)解:如图,连接OD,OE,AE,BF,
∵∠PEA=∠PBF,∠P=∠P,
∴△PAE∽△PFB,
∴,
∴PE PF=PA PB,
∵DE⊥AB,且AB为⊙O的直径,
∴,
∵,
∴∠BOE=∠DFE,
∵∠PFG+∠DFE=180°,∠POE+∠BOE=180°,
∴∠POE=∠PFG,
∵∠P=∠P,
∴△PEO∽△PGF,
∴,
∴PE PF=PO PG,
∴PA PB=PO PG,
设AG=m,则PG=x+m,
∴x(x+2)=(x+1)(x+m),
∴,
∴.
11.【解答】(1)证明:∵OA=OC,
∴∠A=∠ACO,
又∵∠COB=A+∠ACO=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB,
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线;
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P,
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC,
∴;
(3)解:连接MA,MB,
∵点M是的中点,
∴,
∴∠ACM=∠BCM,
∵∠ACM=∠ABM,
∴∠BCM=∠ABM,
∵∠BMN=∠BMC,
∴△MBN∽△MCB,
∴,
∴BM2=MN MC,
又∵AB是⊙O的直径,,
∴∠AMB=90°,AM=BM,
∵AB=6,
∴,
∴.
12.【解答】(1)证明:连接OA并延长交BC于H点,如图,
∵AB=AC,
∴,
∴AH垂直平分BC,
∴AH平分∠BAC,
即∠BAC=2∠BAH,
∵OA=OB,
∴∠ABD=∠BAH,
∴∠BAC=2∠ABD;
(2)解:设∠ABD=α,则∠BAC=2α,
∴∠AED=∠ABD+∠BAC=α+2α=3α,
∵AB为直径,
∴∠BAD=90°,
当AD=AE时,∠ADB=∠AED=3α,
∴α+3α=90°,
解得α=22.5°;
当DA=DE时,∠DAE=∠AED=3α,
∴2α+3α=90°,
解得α=18°,
综上所述,∠ABD的度数为18°或22.5°;
(3)解:∵AH⊥BC,
∴BH=CHBC=3,
在Rt△ABH中,AH4,
设⊙O的半径为r,则OA=OB=r,OH=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,
解得r,
∴BD=2r,
在Rt△ABD中,AD,
在Rt△BCD中,CD,
∵AH∥CD,
∴△AEO∽△CED,
∴,
∴,
∴AE5.
13.【解答】(1)证明:,AM,BN是⊙O的切线,OD平分∠ADC,如图1,过点O作OE⊥CD于点E,则∠OED=90°,
∴∠OAD=90°,∠ADO=∠EDO,
在△OAD和△OED中,
,
∴△OAD≌△OED(AAS),
∴OA=OE,
∵OA是⊙O的半径,
∴OE是⊙O的半径,
∴CD是⊙O的切线;
(2)解:AM,BN,CD是⊙O的切线,⊙O的半径是6,如图2,过点D作DF⊥BC于点F,
∴∠MAO=∠NBO=90°,
∴四边形ABFD是矩形,
∴DF=AB=2r=12,
由切线长定理得:AD=DE,CB=CE,
∵AD=x,BC=y,
∴CF=BC﹣BF=y﹣x,CD=x+y,
在Rt△DCF中,CD2=DF2+CF2,即(x+y)2=122+(y﹣x)2,
化简得;
(3)解:∵梯形ABCD是直角梯形,则cm2,
设AD=x,由(2)可知,
∴,
化简得x2﹣13x+36=0,
解得x=4或x=9,
∴AD长为4cm或9cm.
14.【解答】(1)证明:∵弦AB⊥直径CD,
∴,
∴∠AFC=∠CAB;
(2)证明:如图1,
△CFG是等腰三角形,理由如下:
设AF,BC交于点H,
∵AF⊥BC,
∴∠CHF=90°,
∴∠BCF+∠AFC=90°,
∵CD⊥AB,
∴∠CEB=90°,
∴∠B+∠BCD=90°,
∵,
∴∠ABC=∠AFC,
∴∠BCD=∠BCF,
∴∠CGH=∠AFC,
∴CG=CF,
∴△CFG是等腰三角形;
(3)解:如图2,
连接BG,AD,
由(2)知,
CG=CF,AF⊥BC,∠BCF=∠BAF,
∴CH=FH,∠BDC=∠BCF,
∴BG=BF=4,
∵CD⊥AB,
∴AE=BE,∠DAC=∠BCD,
∴AG=BG=4,∠BAF=∠ACD,
∴∠AEG=∠AEC,
∴△AEG∽△CEA,
∴,
∵AE2+EG2=AG2,
∴(2EG)2+EG2=42,
∴EG,
∴BE=AE=2EG,
∴CE=2AE,
∴CG=CE﹣EG,
∵,
∴∠BAD=∠BCD,
∵∠AED=∠BEC,
∴△AED=∠BEC,
∴△AED∽△CEB,
∴,
∴DE CE=AE BE,
DE,
∴DE,
∴DG=DE+EG,
同理可得,
AG FG=DG CG,
∴4FG,
∴FG,
∴AF=AG+FG.
15.【解答】(1)证明:∵PA与⊙O相切于点A,
∴OA⊥PA,
∵PO平分∠APD,OB⊥PD,
∴OA=OB,
∴OB是圆的半径,
∴PB是⊙O的切线;
(2)解:∵⊙O的半径为2,
∴OA=OB=2,
∵OB⊥PD,OC=4,
∴,AC=OA+OC=2+4=6,
∵PA,PB都是⊙O的切线,
∴设PA=PB=x,则,
∴在Rt△PAC中,PA2+AC2=PC2,
∴,
解得,
∴;
(3)在Rt△BCO中,∠CBO=90°,OC=2OB,
∴∠BCO=30°,∠BOC=60°,
∴∠BOA=120°,
∴,
,,
∴.
16.【解答】(1))证明:连接AD,如图,
∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴∠ADC=∠AGD,
∵四边形AGCD为圆的内接四边形,
∴∠FGC=∠ADC.
∴∠FGC=∠AGD;
(2)解:①连接OG,如图,
∵OA=OG,
∴∠A=∠OGA,
∵AG∥BD,
∴∠B=∠A,
∵∠B=∠AGD,
∴∠A=∠AGD,
∴∠AGD=∠OGA,
∴DG经过点O,
∴O,H重合,即DG为圆的直径,
∴∠GCD=90°,
∴CG⊥DC,
∵CD⊥AB,
∴HE∥GC,
∴△DHE∽△DCG,
∴;
②连接BD,AC,如图,
∵⊙O的半径r,OH=2,BE=1,
∴BH=r﹣2,AH=r+2,HE=r﹣3,AE=2r﹣1,
∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴AD=AC.
∵CG∥AD,
∴,
∴,
∴AC=DG,
∴AD=DG.
∵AB是⊙O的直径,
∴∠ADB=90°,
∵CD⊥AB,
∴△BDE∽△EAD,
∴,
∴DE2=BE AE=1×(2r﹣1)=2r﹣1,
∴ADDG,
∵DH2=DE2+HE2,
∴DH,
∴HG=DG﹣DH.
∵∠DHB=∠GHA,∠AGD=∠DBA,
∴△BDH∽△GAH,
∴,
∴,
∴r3﹣4r2﹣8r+8=0,
∴(r+2)(r2﹣6r+4)=0,
∵r>0,
∴r2﹣6r+4=0,
∴r=3±,
∵由题意:r>3,
∴r=3.
∴⊙O的半径为3.
17.【解答】(1)证明:如图1,连接DF,
∵DC为⊙O的直径,
∴∠DFC=90°,
∴DF⊥BC,
∵BF=CF,
∴DF是BC的垂直平分线,
∴BD=CD,
∴∠B=∠DCB;
(2)解:如图2,连接DF,CE,过点E作EM⊥BC于M,
∵,
∴设DF=3x,BF=4x,
∴BD=CD=5x,
∵∠ACB=90°,
∴∠A+∠B=∠ACD+∠DCB=90°,
∴∠A=∠ACD,
∴AD=CD=5x,
∵DC为⊙O的直径,
∴∠DEC=90°,
由勾股定理得:AC6x,
∵S△ABC AC BC AB CE,
∴ 6x 8x 10x CE,
∴CE=4.8x,
∴DE1.4x,
∵EM⊥BC,AC⊥BC,
∴EM∥AC,
∴△BEM∽△BAC,
∴,
∴,
∴BM=5.12x,EM=3.84x,
∴FM=5.12x﹣4x=1.12x,
在Rt△EFM中,EF2=EM2+FM2,
∴22=(3.84x)2+(1.12x)2,
∴x(负值舍),
∴AC=6x=63,DE=1.4x=1.40.7;
(3)①证明:如图3,延长CA,FE交于点P,连接DG,CE,DF,
∵DE是⊙O的直径,
∴∠DEC=∠DGC=90°,
∴DG⊥AC,
由(1)知:AD=CD=BD,
∴AG=CG,
∵∠DFC=∠DGC=∠FCG=90°,
∴四边形DFCG是矩形,
∴DF=CG,DF∥AC,
∴△DKF∽△CKP,∠P=∠DFE,
∴,
∴CP=3DF,
∴AP=DF,
∵∠DEF=∠PEA,
∴△DEF≌△AEP(AAS),
∴DE=AE,
∴CE是AD的垂直平分线,
∴AC=CD=AD,
∴△ACD是等边三角形,
∴∠ACD=60°,
∴∠DCB=90°﹣60°=30°,
∴∠B=30°;
②解:如图4,延长CA,FE交于点P,连接DF,CE,
∵∠BFD=∠BCA=90°,
∴DF∥AC,
∴△BDF∽△BAC,△DFK∽△CPK,
∴,y,
∴AC=2DF,DF=CP y,
∵tanBx,
∴DF=BF x,
设BF=m,则DF=mx,AC=2mx,
∴y,
由勾股定理得:DCm,
∵∠AEC=∠DFC,∠ACE=∠B=∠DCB,
∴△AEC∽△DFC,
∴,
∴AE,
∴DE=AD﹣AE=CD﹣AE=m,
∵DF∥AP,
∴△DEF∽△AEP,
∴,
∴,
∴AP,
∴y.
18.【解答】(1)解:∵AC=OA,OA=OC,
∴OA=OC=AC,
∴△OAC为等边三角形,
∴∠AOC=∠ACF=60°,
∴,
∵点E是CD中点,OE经过圆心,
∴OE⊥CD,
∴∠EGD=90°﹣∠ADC=60°;
(2)证明:∵∠EGD=60°,
∴∠FGO=∠EGD=60°,
∵∠ACF=60°,
∴∠ACF=∠OGF,
∵∠AFC=∠OFG,
∴△ACF∽△OGF;
(3)解:过点C作CM⊥AD于点M,过点F作FH⊥AO于点H,
由CF=kOF,不妨设OF=1,则CF=k,
∴AC=AO=OC=k+1,
∵∠AOC=60°,
∴,,
∴,
∴在Rt△AFH中,由勾股定理得,,
∵△ACF﹣△OGF,
∴,
∴,
∴,
∵∠CDA=30°,
∴在Rt△CMD 中,,
∴,,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
