2.3.1 认识实数 课件(共22张PPT)
文档属性
| 名称 | 2.3.1 认识实数 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 507.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 07:12:00 | ||
图片预览



文档简介
(共22张PPT)
认识实数
七年级下册 第二章 2.3.1
学习目标
1.理解实数的概念,明确实数包括有理数和无理数,并能对实数进行分类。
2.掌握实数与数轴上的点一一对应的关系,能通过几何模型表示无理数的位置。
3.理解在实数范围内的相反数、倒数、绝对值的意义。
复习回顾
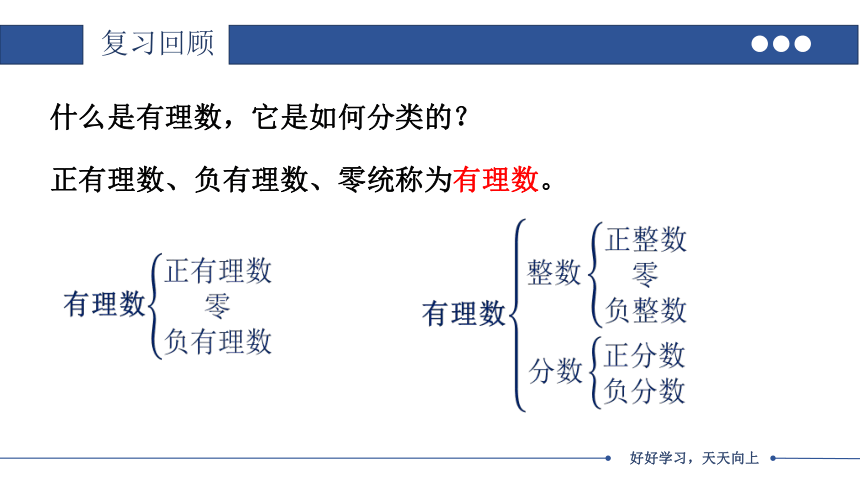
什么是有理数,它是如何分类的?
正有理数、负有理数、零统称为有理数。
有理数
有理数
新知探究
下列各数中,哪些是无理数?
0.,,-,,-,0.101 001…(相邻两个1之间逐次增加一个0).
做一做
无理数:,-,0.101 001…(相邻两个1之间逐次增加一个0).
新知探究
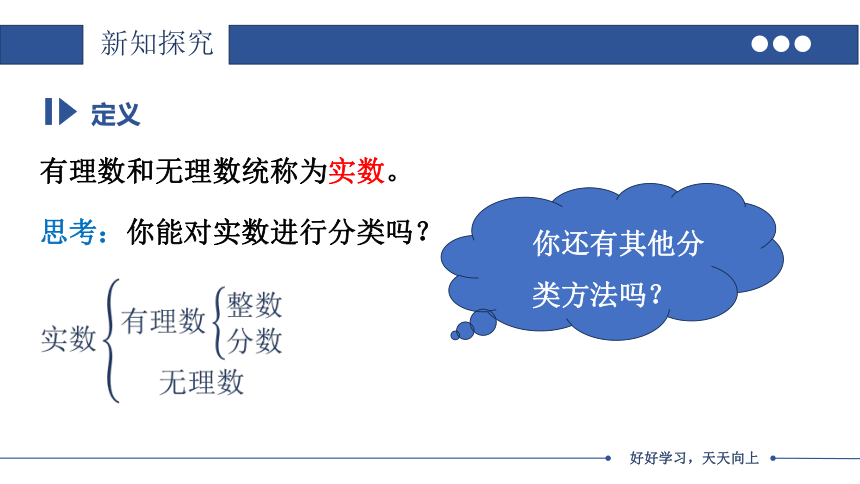
有理数和无理数统称为实数。
定义
思考:你能对实数进行分类吗?
你还有其他分类方法吗?
新知探究
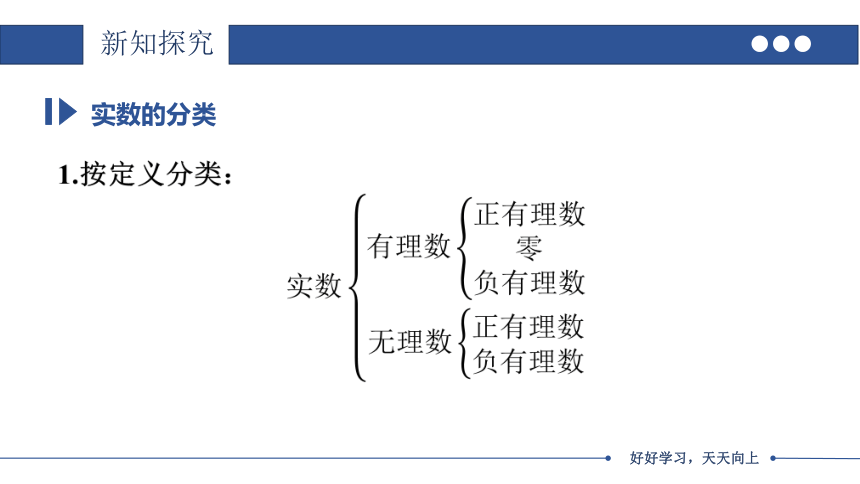
1.按定义分类:
实数的分类
新知探究
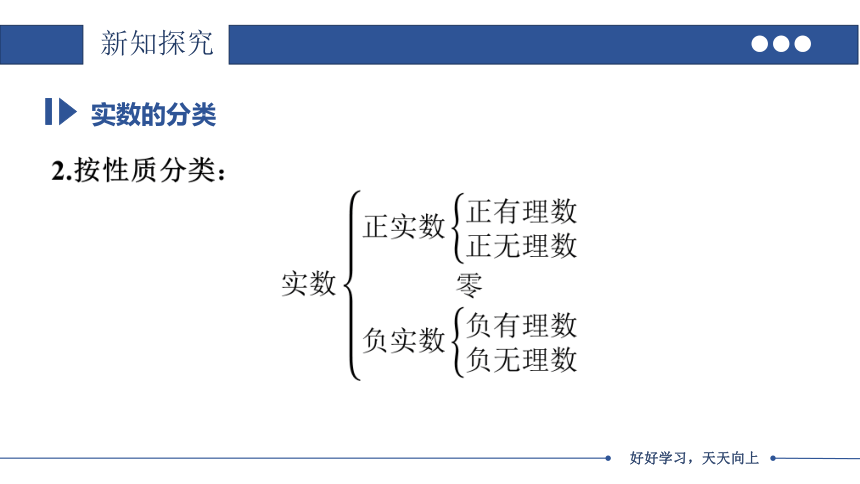
2.按性质分类:
实数的分类
新知探究
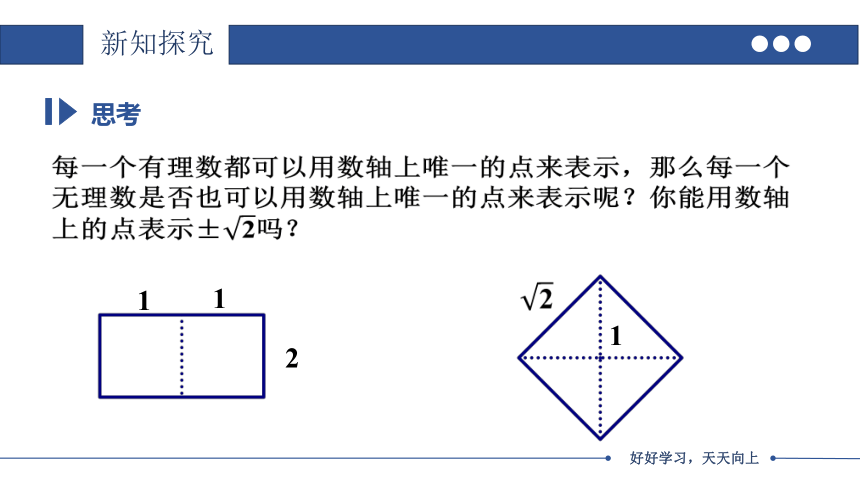
每一个有理数都可以用数轴上唯一的点来表示,那么每一个无理数是否也可以用数轴上唯一的点来表示呢?你能用数轴上的点表示±吗?
思考
1
1
2
1
新知探究
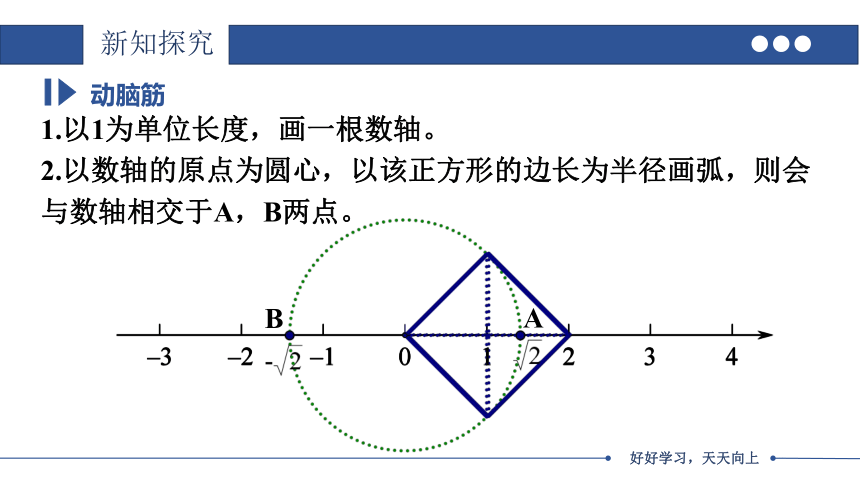
1.以1为单位长度,画一根数轴。
动脑筋
2.以数轴的原点为圆心,以该正方形的边长为半径画弧,则会与数轴相交于A,B两点。
A
B
新知探究
A
B
数轴上有唯一的点A和点B分别表示 和 .
新知探究
事实上,每一个无理数都可以用数轴上唯一的点来表示.
综上可知:
每一个实数都可以用数轴上唯一的点来表示.
反过来,还可以说明:
数轴上每一个点都表示唯一的实数.
将上面两个结论合起来,可以简洁地说成:
实数和数轴上的点一一对应.
新知探究
1.正实数都____________0;
2.负实数都____________ 0;
3.数轴上表示正实数的点在原点____________边,表示负实数的点在原点____________边;
4.如果两个实数只有符号不同,那么其中的一个数叫作另一
个数的____________ ,也称它们互为____________;
5.实数a的相反数记作____________;
6.非零实数a的倒数为____________.
规定
大于
小于
右
左
相反数
相反数
-a
新知探究
1.若实数a,b互为相反数,则a+b=____________;
2.若实数a,b互为倒数,则ab=____________;
3.正实数的绝对值是它____________;
4.负实数的绝对值是它的____________ ;
5. 0的绝对值是____________;
6.
性质
0
1
本身
相反数
0
a
0
-a
例题探究
例1 求下列各数的相反数和绝对值:
(1) π; (2) .
解: (1) π的相反数是π ,= π.
(2)的相反数是 ,=.
1.下列说法中,正确的是 ( )
A.无理数包括正无理数、零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数
课堂练习
C
2.如图,在数轴上表示实数的点可能是 ( )
A. P B. Q C. M D. N
课堂练习
C
3.实数-2的绝对值是 ( )
A.-2
B.2-
C.--2
D. +2
课堂练习
B
4.下列各组数中,互为相反数的一组是 ( )
-2与
B. -2与
C. -2与-
D. |-2|与2
课堂练习
A
课堂小结
实数的分类:
实数和数轴上的点一一对应.
课堂小结
实数的性质:
若实数a,b互为相反数,则a+b=0;
若实数a,b互为倒数,则ab=1;
课后作业
课堂作业:P41 T1、3
家庭作业:《学法》P30 A组(基础一般)
B组(基础较好)
C组(选做)
认识实数
七年级下册 第二章 2.3.1
学习目标
1.理解实数的概念,明确实数包括有理数和无理数,并能对实数进行分类。
2.掌握实数与数轴上的点一一对应的关系,能通过几何模型表示无理数的位置。
3.理解在实数范围内的相反数、倒数、绝对值的意义。
复习回顾
什么是有理数,它是如何分类的?
正有理数、负有理数、零统称为有理数。
有理数
有理数
新知探究
下列各数中,哪些是无理数?
0.,,-,,-,0.101 001…(相邻两个1之间逐次增加一个0).
做一做
无理数:,-,0.101 001…(相邻两个1之间逐次增加一个0).
新知探究
有理数和无理数统称为实数。
定义
思考:你能对实数进行分类吗?
你还有其他分类方法吗?
新知探究
1.按定义分类:
实数的分类
新知探究
2.按性质分类:
实数的分类
新知探究
每一个有理数都可以用数轴上唯一的点来表示,那么每一个无理数是否也可以用数轴上唯一的点来表示呢?你能用数轴上的点表示±吗?
思考
1
1
2
1
新知探究
1.以1为单位长度,画一根数轴。
动脑筋
2.以数轴的原点为圆心,以该正方形的边长为半径画弧,则会与数轴相交于A,B两点。
A
B
新知探究
A
B
数轴上有唯一的点A和点B分别表示 和 .
新知探究
事实上,每一个无理数都可以用数轴上唯一的点来表示.
综上可知:
每一个实数都可以用数轴上唯一的点来表示.
反过来,还可以说明:
数轴上每一个点都表示唯一的实数.
将上面两个结论合起来,可以简洁地说成:
实数和数轴上的点一一对应.
新知探究
1.正实数都____________0;
2.负实数都____________ 0;
3.数轴上表示正实数的点在原点____________边,表示负实数的点在原点____________边;
4.如果两个实数只有符号不同,那么其中的一个数叫作另一
个数的____________ ,也称它们互为____________;
5.实数a的相反数记作____________;
6.非零实数a的倒数为____________.
规定
大于
小于
右
左
相反数
相反数
-a
新知探究
1.若实数a,b互为相反数,则a+b=____________;
2.若实数a,b互为倒数,则ab=____________;
3.正实数的绝对值是它____________;
4.负实数的绝对值是它的____________ ;
5. 0的绝对值是____________;
6.
性质
0
1
本身
相反数
0
a
0
-a
例题探究
例1 求下列各数的相反数和绝对值:
(1) π; (2) .
解: (1) π的相反数是π ,= π.
(2)的相反数是 ,=.
1.下列说法中,正确的是 ( )
A.无理数包括正无理数、零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数
课堂练习
C
2.如图,在数轴上表示实数的点可能是 ( )
A. P B. Q C. M D. N
课堂练习
C
3.实数-2的绝对值是 ( )
A.-2
B.2-
C.--2
D. +2
课堂练习
B
4.下列各组数中,互为相反数的一组是 ( )
-2与
B. -2与
C. -2与-
D. |-2|与2
课堂练习
A
课堂小结
实数的分类:
实数和数轴上的点一一对应.
课堂小结
实数的性质:
若实数a,b互为相反数,则a+b=0;
若实数a,b互为倒数,则ab=1;
课后作业
课堂作业:P41 T1、3
家庭作业:《学法》P30 A组(基础一般)
B组(基础较好)
C组(选做)
同课章节目录
