模型41 定弦定角 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型41 定弦定角 (含答案)2025年中考数学几何模型专题复习 | 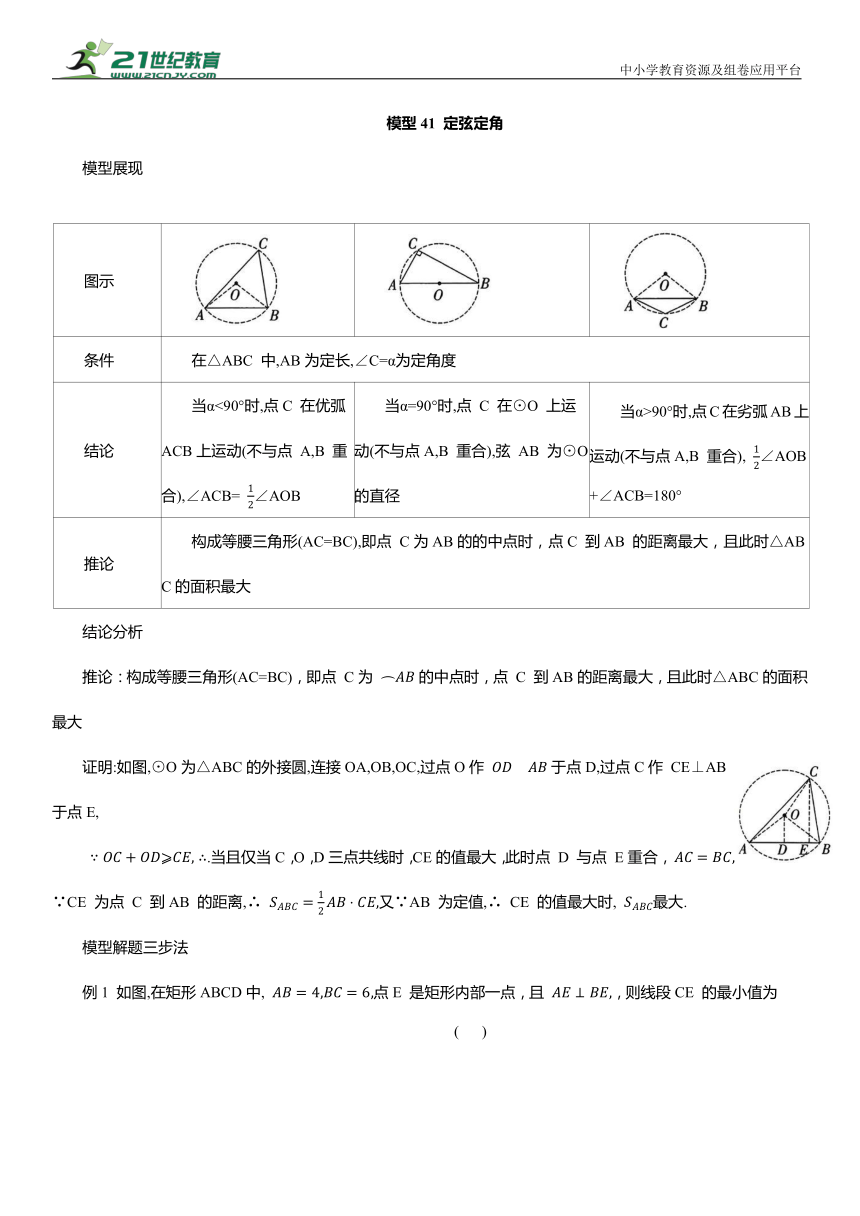 | |
| 格式 | docx | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 08:04:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型41 定弦定角
模型展现
图示
条件 在△ABC 中,AB为定长,∠C=α为定角度
结论 当α<90°时,点C 在优弧ACB上运动(不与点 A,B 重合),∠ACB= ∠AOB 当α=90°时,点 C 在⊙O 上运动(不与点A,B 重合),弦 AB 为⊙O的直径 当α>90°时,点C在劣弧AB上运动(不与点A,B 重合), ∠AOB+∠ACB=180°
推论 构成等腰三角形(AC=BC),即点 C为AB的的中点时,点C 到AB 的距离最大,且此时△ABC的面积最大
结论分析
推论:构成等腰三角形(AC=BC),即点 C为 的中点时,点 C 到AB的距离最大,且此时△ABC的面积最大
证明:如图,⊙O为△ABC的外接圆,连接OA,OB,OC,过点O作 于点D,过点C作 CE⊥AB于点E,
.当且仅当C,O,D三点共线时,CE的值最大,此时点 D 与点 E重合, ∵CE 为点 C 到AB 的距离,∴ 又∵AB 为定值,∴ CE 的值最大时, 最大.
模型解题三步法
例1 如图,在矩形ABCD中, 点E 是矩形内部一点,且 ,则线段CE 的最小值为 ( )
D. 4
例2 如图,在边长为4的等边, 中,点 P 为△ABC内的一个动点,且 则可得出 为定角 面积的最大值为 .
题以类解
1. 如图,在正方形ABCD中,E,F 分别是AB,BC边上的点(不与正方形的顶点重合),CE,DF交于点M,连接BM.若AB=2,∠BCE=∠CDF,则BM 的最小值为 .
2.如图,在菱形AB-CD中, 点 E,F分别在边AB,AD上,且AE=DF,连接DE,BF交于点G,则∠BGD 的度数为 ,四边形BCDG 面积的最大值为 .
3. 如图,在四边形 ABCD 中,∠ABC=∠ADC= 点 P为四边形 ABCD 内一点,且∠BPC=135°,E为AD 边上一点,连接PE,则 PE 的最小值为 .
4.问题提出
(1)如图①,已知 是边长为2的等边三角形,则 的面积为 ;
问题探究
(2)如图②,在 中,已知 求 面积的最大值;
问题解决
(3)如图③,某校学生礼堂的平面示意图为矩形ABCD,其宽AB=20米,长BC=24米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面 CD 上安装一台摄像头 M 进行观测,并且要求恰好能观测到礼堂前端墙面AB区域,同时为了观测效果达到最佳,还需要从点 M 出发的观测角∠AMB=45°.请你通过所学知识进行分析,在墙面CD 区域上是否存在点 M 满足要求 若存在,求出MC的长度;若不存在,请说明理由.
模型解题三步法
例 1 B 【解析】根据定弦定角模型作⊙O,如解图,连接 CO 交⊙O 于点 E',当点 E 位于点E'位置时,线段 CE 取得最小值(点圆最值).∵AB=4,∴OA=OB=OE'=2.∵ BC=
例2 BC 点P ∠BPC
【解析】∵ △ABC 为等边三角形,∴∠ABC=∠ACB=60°,即∠PCA+∠PCB=60°,∵ ∠PBC=∠PCA,∴ ∠PBC+∠PCB=60°,∴ ∠BPC=120°.如解图,根据定弦定角模型作△BPC 的外圆⊙O,连接AO 交 BC于点Q,交 于点 P',当点 P 运动到点 P'(即点A,P',O 三点共线)时,△PBC 的面积最大,由题意得 180°-120°=60°,∴ ∠BOC=120°,∵ △ABC为等边三角形,∴OQ⊥BC,∠BOQ=60°,∴∠OBQ=30°,∠P'BQ=30°,∵BC=4,∴BQ
题以类解
【解析】∵ 四边形ABCD 是正方形,∴ ∠DCF =90°,∴ ∠DCM+∠FCM = 90°,∵ ∠BCE=∠CDF,∴ ∠CDM+∠DCM=90°,∴ ∠DMC=90°.找模型:是否存在定弦:线段CD,是否存在动点:点M,是否存在以动点和
定弦两端点构成的定角:∠DMC.抽离模型:如解图,用模型:根据定弦定角模型作⊙O,连接BO 交⊙O 于点 M',要使 BM 取得最小值,则点B,M,O 三点共线,即M在 M'的位置(点圆最值).∵AB=BC=2,∴ CO=OM'= 此时 即 BM 的最小值为
2. 120°,4 【解析】如解图,连接BD,∵四边形ABCD 是菱形,∠A=60°,∴△ABD 为等边三角形(60°菱形模型),∴ AD = BD,∠A =∠BDF=60°,∵ AE=DF,∴ △ADE≌△DBF(SAS),∴∠ADE=∠DBF,∵ ∠ADE+∠BDE=60°,∴ ∠BDE+∠DBF=60°.∴ ∠DGB =120°.找模型:是否存在定弦:线段 BD,是否存在动点:点G,是否存在以动点和定弦两端点构成的定角:∠DGB.抽离模型:如解图,作△BGD 的外接圆⊙O,用模型:过点 G 作 GH⊥BD于点.H,∵BD=AB=2 ,∴OD=OB=OG=2.∵GH≥OG-OH,∴当O,G,H三点共线时,GH取得最大值,此时OG⊥BD,∠ODB= ∴四边形BCDG面积的最大值为
3. 10 【解析】如解图,作△BPC 的外接圆⊙O,连接OB,OC,OP,在优弧 上任取一点 Q,连接 BQ,CQ.∵ ∠BPC=135°,∴ ∠BQC =45°,∴ ∠BOC =90°,∴ △BOC 为等腰直角三角形. ∴ OP = OB = OC 20,连接OD,过点 O作OH⊥AD 于点H,在△OCD 中, ∠OCD =∠OCB+∠BCD=45°+75°= 120°,∵ OC =20= CD,∴ ∠COD =∠ODC = 30°(△OCD 为等腰三角形),∴ 在Rt△ODH中,∠ODH=∠ADC-∠ODC=60°,∴OH=OD·sin∠ODH 当 PE⊥AD时,则有 OP+PE≥OH,∴PE≥OH-OP=30-20=10,∴PE的最小值为10.
4. 解:(1)
(2)如解图①,作△ABC的外接圆⊙O,∵∠BAC=30°,∴点A在优弧BC上,当点A 与优弧 的中点重合时,△ABC 的面积最大,
过点A作AD⊥BC于点 D,连接OB,OC,
∵∠BAC=30°,∴∠BOC=60°,
∵OB=OC,∴△BOC是等边三角形,
(3)存在.
如解图②,以 AB 为斜边在矩形 ABCD 内作等腰 Rt△AOB,使得∠AOB=90°,再以点 O为圆心,OA 长为半径作圆,并过点 O 作AB的垂线,记垂足为点 E,延长 EO 与⊙O 交于点N,连接AN,BN,则根据圆周角与圆心角的关系可知
∵在等腰Rt△AOB中,AB=20米,OE⊥AB,
米,
米,
米>24米,
则此时∠ANB 的顶点 N 在矩形ABCD 的外侧,∵⊙O与CD有2个交点,
∴在 CD上存在点 M,满足∠AMB=45°.
记⊙O 与 CD 的交点分别为 M ,M ,连接AM ,BM ,OM ,过点 M 作M G⊥AB 于点 G,并过点O作OF⊥M G于点 F.
故可得OE=FG,
又∵在 Rt△M OF 中, 米, 米,
2米,
米,同理,M C=EB+OF=10+2=12米.
综上所述,在墙面CD 区域存在两个满足要求的点 M,满足∠AMB=45°,且 MC 的长度为8米或12米.
模型41 定弦定角
模型展现
图示
条件 在△ABC 中,AB为定长,∠C=α为定角度
结论 当α<90°时,点C 在优弧ACB上运动(不与点 A,B 重合),∠ACB= ∠AOB 当α=90°时,点 C 在⊙O 上运动(不与点A,B 重合),弦 AB 为⊙O的直径 当α>90°时,点C在劣弧AB上运动(不与点A,B 重合), ∠AOB+∠ACB=180°
推论 构成等腰三角形(AC=BC),即点 C为AB的的中点时,点C 到AB 的距离最大,且此时△ABC的面积最大
结论分析
推论:构成等腰三角形(AC=BC),即点 C为 的中点时,点 C 到AB的距离最大,且此时△ABC的面积最大
证明:如图,⊙O为△ABC的外接圆,连接OA,OB,OC,过点O作 于点D,过点C作 CE⊥AB于点E,
.当且仅当C,O,D三点共线时,CE的值最大,此时点 D 与点 E重合, ∵CE 为点 C 到AB 的距离,∴ 又∵AB 为定值,∴ CE 的值最大时, 最大.
模型解题三步法
例1 如图,在矩形ABCD中, 点E 是矩形内部一点,且 ,则线段CE 的最小值为 ( )
D. 4
例2 如图,在边长为4的等边, 中,点 P 为△ABC内的一个动点,且 则可得出 为定角 面积的最大值为 .
题以类解
1. 如图,在正方形ABCD中,E,F 分别是AB,BC边上的点(不与正方形的顶点重合),CE,DF交于点M,连接BM.若AB=2,∠BCE=∠CDF,则BM 的最小值为 .
2.如图,在菱形AB-CD中, 点 E,F分别在边AB,AD上,且AE=DF,连接DE,BF交于点G,则∠BGD 的度数为 ,四边形BCDG 面积的最大值为 .
3. 如图,在四边形 ABCD 中,∠ABC=∠ADC= 点 P为四边形 ABCD 内一点,且∠BPC=135°,E为AD 边上一点,连接PE,则 PE 的最小值为 .
4.问题提出
(1)如图①,已知 是边长为2的等边三角形,则 的面积为 ;
问题探究
(2)如图②,在 中,已知 求 面积的最大值;
问题解决
(3)如图③,某校学生礼堂的平面示意图为矩形ABCD,其宽AB=20米,长BC=24米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面 CD 上安装一台摄像头 M 进行观测,并且要求恰好能观测到礼堂前端墙面AB区域,同时为了观测效果达到最佳,还需要从点 M 出发的观测角∠AMB=45°.请你通过所学知识进行分析,在墙面CD 区域上是否存在点 M 满足要求 若存在,求出MC的长度;若不存在,请说明理由.
模型解题三步法
例 1 B 【解析】根据定弦定角模型作⊙O,如解图,连接 CO 交⊙O 于点 E',当点 E 位于点E'位置时,线段 CE 取得最小值(点圆最值).∵AB=4,∴OA=OB=OE'=2.∵ BC=
例2 BC 点P ∠BPC
【解析】∵ △ABC 为等边三角形,∴∠ABC=∠ACB=60°,即∠PCA+∠PCB=60°,∵ ∠PBC=∠PCA,∴ ∠PBC+∠PCB=60°,∴ ∠BPC=120°.如解图,根据定弦定角模型作△BPC 的外圆⊙O,连接AO 交 BC于点Q,交 于点 P',当点 P 运动到点 P'(即点A,P',O 三点共线)时,△PBC 的面积最大,由题意得 180°-120°=60°,∴ ∠BOC=120°,∵ △ABC为等边三角形,∴OQ⊥BC,∠BOQ=60°,∴∠OBQ=30°,∠P'BQ=30°,∵BC=4,∴BQ
题以类解
【解析】∵ 四边形ABCD 是正方形,∴ ∠DCF =90°,∴ ∠DCM+∠FCM = 90°,∵ ∠BCE=∠CDF,∴ ∠CDM+∠DCM=90°,∴ ∠DMC=90°.找模型:是否存在定弦:线段CD,是否存在动点:点M,是否存在以动点和
定弦两端点构成的定角:∠DMC.抽离模型:如解图,用模型:根据定弦定角模型作⊙O,连接BO 交⊙O 于点 M',要使 BM 取得最小值,则点B,M,O 三点共线,即M在 M'的位置(点圆最值).∵AB=BC=2,∴ CO=OM'= 此时 即 BM 的最小值为
2. 120°,4 【解析】如解图,连接BD,∵四边形ABCD 是菱形,∠A=60°,∴△ABD 为等边三角形(60°菱形模型),∴ AD = BD,∠A =∠BDF=60°,∵ AE=DF,∴ △ADE≌△DBF(SAS),∴∠ADE=∠DBF,∵ ∠ADE+∠BDE=60°,∴ ∠BDE+∠DBF=60°.∴ ∠DGB =120°.找模型:是否存在定弦:线段 BD,是否存在动点:点G,是否存在以动点和定弦两端点构成的定角:∠DGB.抽离模型:如解图,作△BGD 的外接圆⊙O,用模型:过点 G 作 GH⊥BD于点.H,∵BD=AB=2 ,∴OD=OB=OG=2.∵GH≥OG-OH,∴当O,G,H三点共线时,GH取得最大值,此时OG⊥BD,∠ODB= ∴四边形BCDG面积的最大值为
3. 10 【解析】如解图,作△BPC 的外接圆⊙O,连接OB,OC,OP,在优弧 上任取一点 Q,连接 BQ,CQ.∵ ∠BPC=135°,∴ ∠BQC =45°,∴ ∠BOC =90°,∴ △BOC 为等腰直角三角形. ∴ OP = OB = OC 20,连接OD,过点 O作OH⊥AD 于点H,在△OCD 中, ∠OCD =∠OCB+∠BCD=45°+75°= 120°,∵ OC =20= CD,∴ ∠COD =∠ODC = 30°(△OCD 为等腰三角形),∴ 在Rt△ODH中,∠ODH=∠ADC-∠ODC=60°,∴OH=OD·sin∠ODH 当 PE⊥AD时,则有 OP+PE≥OH,∴PE≥OH-OP=30-20=10,∴PE的最小值为10.
4. 解:(1)
(2)如解图①,作△ABC的外接圆⊙O,∵∠BAC=30°,∴点A在优弧BC上,当点A 与优弧 的中点重合时,△ABC 的面积最大,
过点A作AD⊥BC于点 D,连接OB,OC,
∵∠BAC=30°,∴∠BOC=60°,
∵OB=OC,∴△BOC是等边三角形,
(3)存在.
如解图②,以 AB 为斜边在矩形 ABCD 内作等腰 Rt△AOB,使得∠AOB=90°,再以点 O为圆心,OA 长为半径作圆,并过点 O 作AB的垂线,记垂足为点 E,延长 EO 与⊙O 交于点N,连接AN,BN,则根据圆周角与圆心角的关系可知
∵在等腰Rt△AOB中,AB=20米,OE⊥AB,
米,
米,
米>24米,
则此时∠ANB 的顶点 N 在矩形ABCD 的外侧,∵⊙O与CD有2个交点,
∴在 CD上存在点 M,满足∠AMB=45°.
记⊙O 与 CD 的交点分别为 M ,M ,连接AM ,BM ,OM ,过点 M 作M G⊥AB 于点 G,并过点O作OF⊥M G于点 F.
故可得OE=FG,
又∵在 Rt△M OF 中, 米, 米,
2米,
米,同理,M C=EB+OF=10+2=12米.
综上所述,在墙面CD 区域存在两个满足要求的点 M,满足∠AMB=45°,且 MC 的长度为8米或12米.
同课章节目录
