模型53 “阿氏圆”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型53 “阿氏圆”模型(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:25:23 | ||
图片预览


文档简介
模型53 “阿氏圆”模型
基础模型
图示
条件 点P是半径为r的⊙O上一动点,点A,B为⊙O外两定点
问题 当r,k满足r=k·OA(0结论分析
如图,点P是半径为r的⊙O上一动点,点A,B为圆外的定点,且 如何确定点 P的位置,使得 的值最小.
一找:找带有系数k的线段AP;
二构:在线段OA上取一点C,构造
①在线段OA上截取OC,使(
②连接PC,OP,证明
三转化:通过相似三角形的对应边成比例,将kPA转化为PC;
四求解:使得 利用“两点之间线段最短”转化为求BC的长.
模型拓展
拓展方向:拓展“阿氏圆”与“胡不归”之间的关系
共同点 平面上有一动点P,两定点A,B,如何确定点P 的位置,求解形如kAP+BP的最值
不同点 1.轨迹不同:若点 P的轨迹为一条直线,则考虑“胡不归”模型;若点P的轨迹为圆或圆 的一部分,则考虑“阿氏圆”模型: 2.解题方法不同:“胡不归”模型是利用锐角三角函数和垂线段最短解题;“阿氏圆”模 型是利用“A字”型相似三角形解题
模型解题三步法
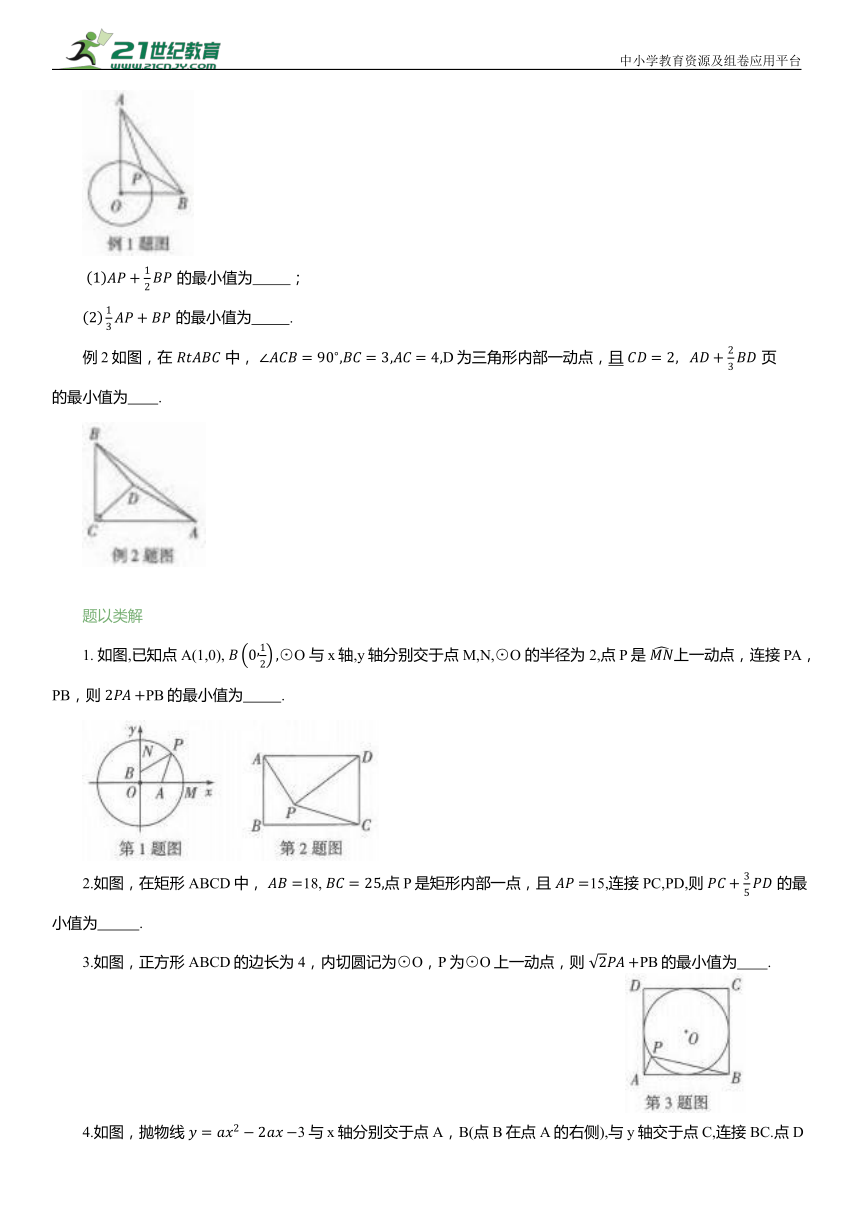
例1 如图,在 中, ⊙O 的半径为2,点P为⊙O上一动点.
的最小值为 ;
的最小值为 .
例2如图,在 中, D为三角形内部一动点,且 页 的最小值为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,已知点A(1,0), ⊙O 与x轴,y轴分别交于点 M,N,⊙O 的半径为2,点P是 上一动点,连接PA,PB,则 PB的最小值为 .
2.如图,在矩形ABCD中, 18, 点P是矩形内部一点,且 15,连接 PC,PD,则 的最小值为 .
3.如图,正方形ABCD的边长为4,内切圆记为⊙O,P为⊙O上一动点,则 PB的最小值为 .
4.如图,抛物线 3与x轴分别交于点A,B(点B在点A的右侧),与y轴交于点C,连接BC.点D 与点 C关于原点O 对称,作射线BD 交抛物线于点E,且
(1)求抛物线的表达式;
(2)过点B作 交抛物线的对称轴于点 F,以点 C 为圆心,以 的长为半径作⊙C,点T为⊙C上的一个动点,求 的最小值.
模型解题三步法
例1 (1) 【解析】根据“阿氏圆”模型作
解图①, (两组对应边成比例且夹角相等的两个三角形相似), 连接AC 与⊙O 交于点 P',点 P'即为使得. 最小时的点 P,此时 的最小值为AC 的长(点圆最值), OA=6,∠AOC=90°,∴在 Rt△AOC 中,AC= 的最小值为
【解析】找模型:圆上是否存在一动点:点P,圆外是否存在两定点:点A和点B,是否求一动点和两定点构造线段和的最小值,且一条线段带系数: 抽离模型:如解图,用模型 根据“阿氏圆”模型作解图②,∴△OPD∽△OAP(两组对应边成比例且夹角相等的两个三角形相似),∴ BP,连接BD与⊙O 交于点 P',点 P'即为使得 的值最小时的点 P,此时 BP 的最小值为 BD 的长(点圆最值),∵ OD ∴在Rt△BOD 中,
的最小值为
例2 点D 点A 和点 B
【解析】根据“阿氏圆”模型作图如解图,∴ △MCD∽△DCB(两组对应边成比例且夹角相等的两个三角形相似), 则 连接AM交⊙C 于点 D',点 D'即为 的值最小时的点 D,其最小值为 AM 的长(点圆最值), = ,AC=4,∠ACB =90°,∴在 Rt△AMC 中, 的最小值为
题以类解
【解析】找模型:圆上是否存在一动点:点P,圆内是否存在两定点:点A 和点 B,是否求一动点和两定点构造线段和的最小值,且一条线段带系数:2PA+PB.抽离模型:如解图,用模型:根据“阿氏圆”模型,在OA的延长线上作 OH=4,连接BH,OP,PH,∵ ∠POH,∴△AOP∽△POH(两组对应边成比例且夹角相等的两个三角形相似), = ,∴HP=2PA,∴2PA+PB=HP+PB,∴当B,P,H三点共线时,2PA+PB 有最小值,最小值为HB 的长(点圆最值),在 Rt△BOH中, 的最小值为
【解析】找模型1:是否存在一动点:点 P,是否存在一定点:点A,是否存在一定线段:AP,故根据定点定长确定圆作以点A为圆心,AP长为半径的圆弧,点P 在圆弧上运动.找模型2:是否存在圆上一动点:点P,是否存在圆外两定点:点C 和点 D,是否求一动点和两定点构造线段和的最小值,且一条线段带系数: 抽离模型:如解图,用模型:根据“阿氏圆”模型在线段AD 上作 ∵四边形 ABCD 是矩形,∴ =∠DAP,∴△PAE∽△DAP(两组对应边成比例且夹角相等的两个三角形相似), 连接CE交⊙A 于点 P',∴当点 P,P'重合时, 取得最小值,CE 即为 最小时的长(点圆最值),在 Rt△CDE 中,CD=18,DE=AD-AE=16,∴ CE= 18 +16 = 的最小值为
3. 2 【解析】如解图,连接OP,OB,设⊙O的半径为r,则 2 ,取OB的中点I,连接PI,AI,∴OI=IB= OBP,∠O是公共角,∴△BOP∽△POI(两组对应边成比例且夹角相等的两个三角形相似), AP+PI(“阿氏圆”模型),∴当A,P,I在一条直线上时, 最小,最小值为 AI的长,过点I作IE⊥AB 于点 D E,∵∠ABO=45°,∴IE= 的最小值为 的最小值是
4. 解:(1)由题意得,C(0,-3),
∵点D与C关于原点O对称,
∴点D(0,3),
∵BD=DE,
∴点 D 为BE的中点,
设点B(m,0),则点E(-m,6),
将点B(m,0),E(-m,6)代入抛物线 2ax-3中,
得
解得
∴抛物线的表达式为
(2)∵抛物线
∴抛物线的对称轴为直线x=1,
令y=0,则
解得
∴OB=4,
如解图,设直线x=1与x轴的交点为 Q,则∠FQB=90°,
∴∠QFB+∠QBF=90°,
∵BF⊥BC,
∴∠FBC=90°,
∴∠OBC+∠QBF=90°,
∴∠QFB=∠OBC,
∵BQ=4-1=3,OC=3,
∴BQ=OC,
又∵∠FQB=∠BOC=90°,
∴△FQB≌△BOC,
∴BF=CB.
在Rt△BOC中,OB=4,OC=3,由勾股定理得BC=5,
∴BF=BC=5,
在CB上截取 CG=1,连接GT,CT,则 GB=5-1=4,
又∵∠GCT=∠TCB,
即
∵点F(1,4)为定点,∴当F,T,G三点共线时, 的值最小,最小值为线段GF的长,在Rt△GBF中,GB=4,BF=5,由勾股定理得
的最小值为
基础模型
图示
条件 点P是半径为r的⊙O上一动点,点A,B为⊙O外两定点
问题 当r,k满足r=k·OA(0
如图,点P是半径为r的⊙O上一动点,点A,B为圆外的定点,且 如何确定点 P的位置,使得 的值最小.
一找:找带有系数k的线段AP;
二构:在线段OA上取一点C,构造
①在线段OA上截取OC,使(
②连接PC,OP,证明
三转化:通过相似三角形的对应边成比例,将kPA转化为PC;
四求解:使得 利用“两点之间线段最短”转化为求BC的长.
模型拓展
拓展方向:拓展“阿氏圆”与“胡不归”之间的关系
共同点 平面上有一动点P,两定点A,B,如何确定点P 的位置,求解形如kAP+BP的最值
不同点 1.轨迹不同:若点 P的轨迹为一条直线,则考虑“胡不归”模型;若点P的轨迹为圆或圆 的一部分,则考虑“阿氏圆”模型: 2.解题方法不同:“胡不归”模型是利用锐角三角函数和垂线段最短解题;“阿氏圆”模 型是利用“A字”型相似三角形解题
模型解题三步法
例1 如图,在 中, ⊙O 的半径为2,点P为⊙O上一动点.
的最小值为 ;
的最小值为 .
例2如图,在 中, D为三角形内部一动点,且 页 的最小值为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,已知点A(1,0), ⊙O 与x轴,y轴分别交于点 M,N,⊙O 的半径为2,点P是 上一动点,连接PA,PB,则 PB的最小值为 .
2.如图,在矩形ABCD中, 18, 点P是矩形内部一点,且 15,连接 PC,PD,则 的最小值为 .
3.如图,正方形ABCD的边长为4,内切圆记为⊙O,P为⊙O上一动点,则 PB的最小值为 .
4.如图,抛物线 3与x轴分别交于点A,B(点B在点A的右侧),与y轴交于点C,连接BC.点D 与点 C关于原点O 对称,作射线BD 交抛物线于点E,且
(1)求抛物线的表达式;
(2)过点B作 交抛物线的对称轴于点 F,以点 C 为圆心,以 的长为半径作⊙C,点T为⊙C上的一个动点,求 的最小值.
模型解题三步法
例1 (1) 【解析】根据“阿氏圆”模型作
解图①, (两组对应边成比例且夹角相等的两个三角形相似), 连接AC 与⊙O 交于点 P',点 P'即为使得. 最小时的点 P,此时 的最小值为AC 的长(点圆最值), OA=6,∠AOC=90°,∴在 Rt△AOC 中,AC= 的最小值为
【解析】找模型:圆上是否存在一动点:点P,圆外是否存在两定点:点A和点B,是否求一动点和两定点构造线段和的最小值,且一条线段带系数: 抽离模型:如解图,用模型 根据“阿氏圆”模型作解图②,∴△OPD∽△OAP(两组对应边成比例且夹角相等的两个三角形相似),∴ BP,连接BD与⊙O 交于点 P',点 P'即为使得 的值最小时的点 P,此时 BP 的最小值为 BD 的长(点圆最值),∵ OD ∴在Rt△BOD 中,
的最小值为
例2 点D 点A 和点 B
【解析】根据“阿氏圆”模型作图如解图,∴ △MCD∽△DCB(两组对应边成比例且夹角相等的两个三角形相似), 则 连接AM交⊙C 于点 D',点 D'即为 的值最小时的点 D,其最小值为 AM 的长(点圆最值), = ,AC=4,∠ACB =90°,∴在 Rt△AMC 中, 的最小值为
题以类解
【解析】找模型:圆上是否存在一动点:点P,圆内是否存在两定点:点A 和点 B,是否求一动点和两定点构造线段和的最小值,且一条线段带系数:2PA+PB.抽离模型:如解图,用模型:根据“阿氏圆”模型,在OA的延长线上作 OH=4,连接BH,OP,PH,∵ ∠POH,∴△AOP∽△POH(两组对应边成比例且夹角相等的两个三角形相似), = ,∴HP=2PA,∴2PA+PB=HP+PB,∴当B,P,H三点共线时,2PA+PB 有最小值,最小值为HB 的长(点圆最值),在 Rt△BOH中, 的最小值为
【解析】找模型1:是否存在一动点:点 P,是否存在一定点:点A,是否存在一定线段:AP,故根据定点定长确定圆作以点A为圆心,AP长为半径的圆弧,点P 在圆弧上运动.找模型2:是否存在圆上一动点:点P,是否存在圆外两定点:点C 和点 D,是否求一动点和两定点构造线段和的最小值,且一条线段带系数: 抽离模型:如解图,用模型:根据“阿氏圆”模型在线段AD 上作 ∵四边形 ABCD 是矩形,∴ =∠DAP,∴△PAE∽△DAP(两组对应边成比例且夹角相等的两个三角形相似), 连接CE交⊙A 于点 P',∴当点 P,P'重合时, 取得最小值,CE 即为 最小时的长(点圆最值),在 Rt△CDE 中,CD=18,DE=AD-AE=16,∴ CE= 18 +16 = 的最小值为
3. 2 【解析】如解图,连接OP,OB,设⊙O的半径为r,则 2 ,取OB的中点I,连接PI,AI,∴OI=IB= OBP,∠O是公共角,∴△BOP∽△POI(两组对应边成比例且夹角相等的两个三角形相似), AP+PI(“阿氏圆”模型),∴当A,P,I在一条直线上时, 最小,最小值为 AI的长,过点I作IE⊥AB 于点 D E,∵∠ABO=45°,∴IE= 的最小值为 的最小值是
4. 解:(1)由题意得,C(0,-3),
∵点D与C关于原点O对称,
∴点D(0,3),
∵BD=DE,
∴点 D 为BE的中点,
设点B(m,0),则点E(-m,6),
将点B(m,0),E(-m,6)代入抛物线 2ax-3中,
得
解得
∴抛物线的表达式为
(2)∵抛物线
∴抛物线的对称轴为直线x=1,
令y=0,则
解得
∴OB=4,
如解图,设直线x=1与x轴的交点为 Q,则∠FQB=90°,
∴∠QFB+∠QBF=90°,
∵BF⊥BC,
∴∠FBC=90°,
∴∠OBC+∠QBF=90°,
∴∠QFB=∠OBC,
∵BQ=4-1=3,OC=3,
∴BQ=OC,
又∵∠FQB=∠BOC=90°,
∴△FQB≌△BOC,
∴BF=CB.
在Rt△BOC中,OB=4,OC=3,由勾股定理得BC=5,
∴BF=BC=5,
在CB上截取 CG=1,连接GT,CT,则 GB=5-1=4,
又∵∠GCT=∠TCB,
即
∵点F(1,4)为定点,∴当F,T,G三点共线时, 的值最小,最小值为线段GF的长,在Rt△GBF中,GB=4,BF=5,由勾股定理得
的最小值为
同课章节目录
