模型55 “布洛卡点”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型55 “布洛卡点”模型(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 233.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:30:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
模型55 “布洛卡点”模型
基础模型
图示
点P是△ABC内部一点,连接AP,BP,CP,∠1=∠2=∠3
模型拓展
拓展方向:由一般三角形到特殊三角形.
类型 等腰三角形 直角三角形
图示
条件 在△ABC中,AB=AC,点 P 为△ABC 内部一点,连接AP,BP,CP,∠1=∠2=∠3 在△ABC 中,AB=AC,∠BAC=90°,点 P 为△ABC内部一点,连接AP,BP,CP,∠1=∠2=∠3
结论 1. △ABP∽△BCP; 2. PB =PA·PC 1. △ABP∽△BCP; 2. ∠APC=90°; 3. tan∠ACP= 即CP=2AP; 4.若点 P到三角形的边AB,BC,AC的距离分别是h ,h ,h ,则h =h ·h
模型解题三步法
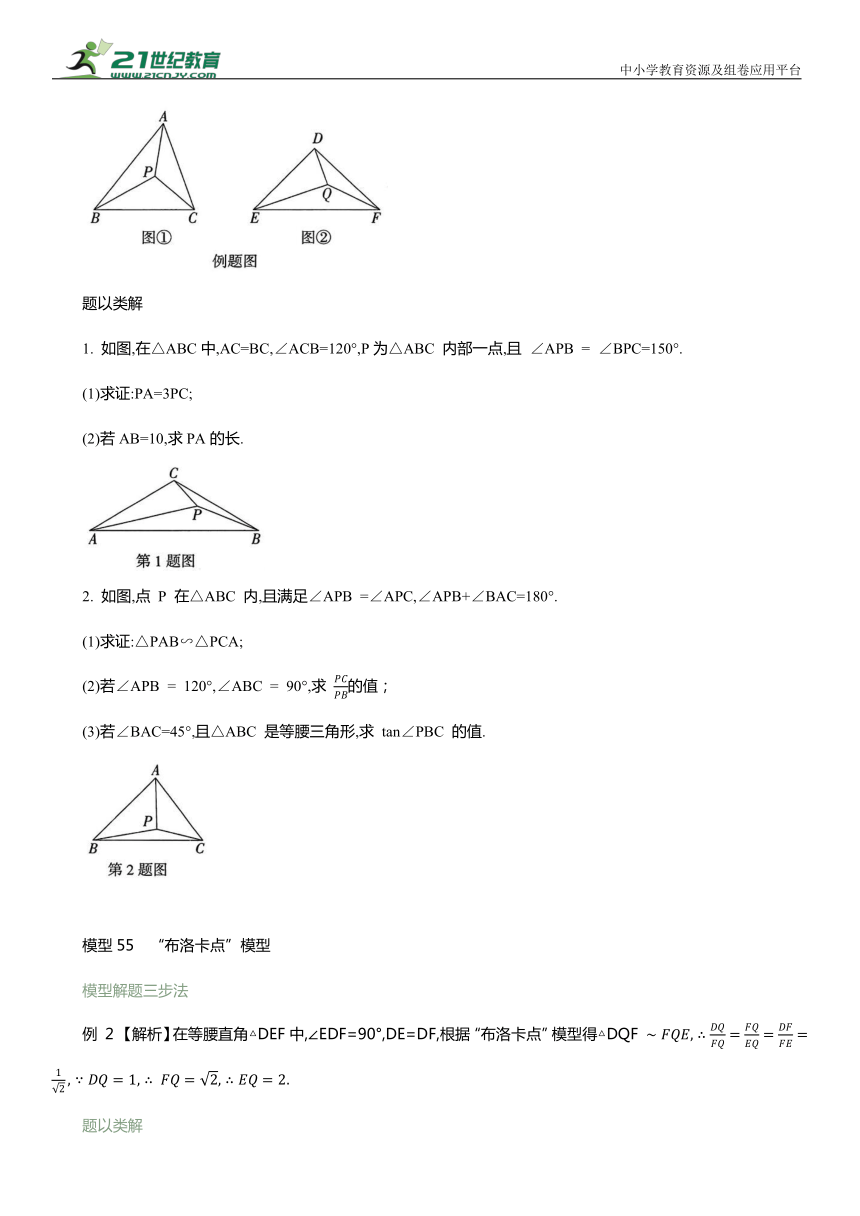
例 如图①,△ABC内有一点 P,满足. ,那么点 P 被称为△ABC 的“布洛卡点”.如图②,在△DEF中, ,若点 Q 是△DEF的一个“布洛卡点”,DQ=1,则EQ 的长为 .
题以类解
1. 如图,在△ABC中,AC=BC,∠ACB=120°,P为△ABC 内部一点,且 ∠APB = ∠BPC=150°.
(1)求证:PA=3PC;
(2)若AB=10,求PA的长.
2. 如图,点 P 在△ABC 内,且满足∠APB =∠APC,∠APB+∠BAC=180°.
(1)求证:△PAB∽△PCA;
(2)若∠APB = 120°,∠ABC = 90°,求 的值;
(3)若∠BAC=45°,且△ABC 是等腰三角形,求 tan∠PBC 的值.
模型55 “布洛卡点”模型
模型解题三步法
例 2 【解析】在等腰直角△DEF中,∠EDF=90°,DE=DF,根据“布洛卡点”模型得△DQF
题以类解
1. (1)证明:如解图,过点 C 作 CD⊥AB 于点D.
∵在△ABC中,AC=BC,∠ACB=120°,
∠ACB)=30°,
∵在 Rt△CDB中,∠CBD=30°,
∵∠CAP+∠3=30°,∠1+∠2=30°,
∠APB=∠BPC=150°,
∴∠3+∠2=∠PCB+∠1=30°,
即∠CAP=∠2=∠PCB,
∴ 点 P 是△ACB 的一个“布洛卡点”,
∴ △PAB∽△PBC(“布洛卡点”模型),
(2)解:如解图,将线段 BP 绕点 B 顺时针旋转60°得到 BP',连接 PP',CP',则△BPP'为等边三角形,
∴∠5=∠BPC-∠4=150°-60°=90°,
∵在 Rt△PP'C中,.
∴∠6=30°,
∴P'C=2PC,
∴在 Rt△BCP'中, 由(1)中 可得 在Rt△CP'B中, (负值已舍去),
由(1)得 PA=3PC,
2. (1)证明:∵ ∠APB+∠BAC=180°,
即 +∠CAP,
∴∠ABP=∠CAP,
又∵∠APB=∠APC,
∴△PAB∽△PCA;
(2)解:如解图①,
∵∠APB+∠BAC=180°,∠APB=120°,
∴∠BAC=60°,
在△ABC中,∵∠ABC=90°,∠BAC=60°,
又∵△PAB∽△PCA,
即
(3)解:∵ ∠BAC = 45°,∠APB +∠BAC =180°,∠APB=∠APC,
∴∠APB=∠APC=135°.
∵△PCA∽△PAB,
①如解图②,
当△ABC 是等腰三角形,且 AB = AC 时,
②如解图③,
当△ABC 是等腰三角形,且 AB = BC 时,∠ACB=∠BAC=45°,∠ABC=90°,
③如解图④,
当△ABC 是等腰三角形,且 AC = BC 时,∠ABC=∠BAC=45°,∠ACB=90°,
综上所述,tan∠PBC的值为1或2或
模型55 “布洛卡点”模型
基础模型
图示
点P是△ABC内部一点,连接AP,BP,CP,∠1=∠2=∠3
模型拓展
拓展方向:由一般三角形到特殊三角形.
类型 等腰三角形 直角三角形
图示
条件 在△ABC中,AB=AC,点 P 为△ABC 内部一点,连接AP,BP,CP,∠1=∠2=∠3 在△ABC 中,AB=AC,∠BAC=90°,点 P 为△ABC内部一点,连接AP,BP,CP,∠1=∠2=∠3
结论 1. △ABP∽△BCP; 2. PB =PA·PC 1. △ABP∽△BCP; 2. ∠APC=90°; 3. tan∠ACP= 即CP=2AP; 4.若点 P到三角形的边AB,BC,AC的距离分别是h ,h ,h ,则h =h ·h
模型解题三步法
例 如图①,△ABC内有一点 P,满足. ,那么点 P 被称为△ABC 的“布洛卡点”.如图②,在△DEF中, ,若点 Q 是△DEF的一个“布洛卡点”,DQ=1,则EQ 的长为 .
题以类解
1. 如图,在△ABC中,AC=BC,∠ACB=120°,P为△ABC 内部一点,且 ∠APB = ∠BPC=150°.
(1)求证:PA=3PC;
(2)若AB=10,求PA的长.
2. 如图,点 P 在△ABC 内,且满足∠APB =∠APC,∠APB+∠BAC=180°.
(1)求证:△PAB∽△PCA;
(2)若∠APB = 120°,∠ABC = 90°,求 的值;
(3)若∠BAC=45°,且△ABC 是等腰三角形,求 tan∠PBC 的值.
模型55 “布洛卡点”模型
模型解题三步法
例 2 【解析】在等腰直角△DEF中,∠EDF=90°,DE=DF,根据“布洛卡点”模型得△DQF
题以类解
1. (1)证明:如解图,过点 C 作 CD⊥AB 于点D.
∵在△ABC中,AC=BC,∠ACB=120°,
∠ACB)=30°,
∵在 Rt△CDB中,∠CBD=30°,
∵∠CAP+∠3=30°,∠1+∠2=30°,
∠APB=∠BPC=150°,
∴∠3+∠2=∠PCB+∠1=30°,
即∠CAP=∠2=∠PCB,
∴ 点 P 是△ACB 的一个“布洛卡点”,
∴ △PAB∽△PBC(“布洛卡点”模型),
(2)解:如解图,将线段 BP 绕点 B 顺时针旋转60°得到 BP',连接 PP',CP',则△BPP'为等边三角形,
∴∠5=∠BPC-∠4=150°-60°=90°,
∵在 Rt△PP'C中,.
∴∠6=30°,
∴P'C=2PC,
∴在 Rt△BCP'中, 由(1)中 可得 在Rt△CP'B中, (负值已舍去),
由(1)得 PA=3PC,
2. (1)证明:∵ ∠APB+∠BAC=180°,
即 +∠CAP,
∴∠ABP=∠CAP,
又∵∠APB=∠APC,
∴△PAB∽△PCA;
(2)解:如解图①,
∵∠APB+∠BAC=180°,∠APB=120°,
∴∠BAC=60°,
在△ABC中,∵∠ABC=90°,∠BAC=60°,
又∵△PAB∽△PCA,
即
(3)解:∵ ∠BAC = 45°,∠APB +∠BAC =180°,∠APB=∠APC,
∴∠APB=∠APC=135°.
∵△PCA∽△PAB,
①如解图②,
当△ABC 是等腰三角形,且 AB = AC 时,
②如解图③,
当△ABC 是等腰三角形,且 AB = BC 时,∠ACB=∠BAC=45°,∠ABC=90°,
③如解图④,
当△ABC 是等腰三角形,且 AC = BC 时,∠ABC=∠BAC=45°,∠ACB=90°,
综上所述,tan∠PBC的值为1或2或
同课章节目录
