模型57 “12345”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型57 “12345”模型(含答案)2025年中考数学几何模型专题复习 | 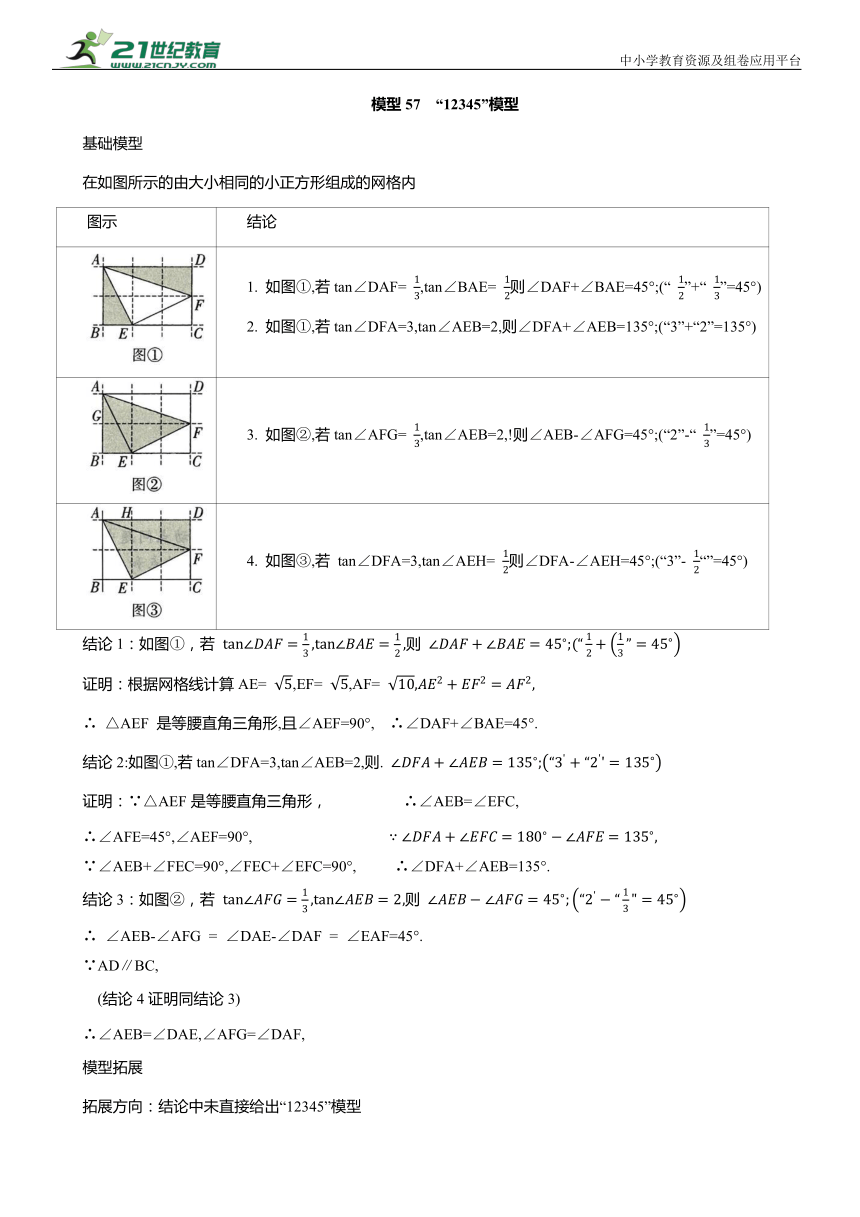 | |
| 格式 | docx | ||
| 文件大小 | 349.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:30:15 | ||
图片预览

文档简介
模型57 “12345”模型
基础模型
在如图所示的由大小相同的小正方形组成的网格内
图示 结论
1. 如图①,若tan∠DAF= ,tan∠BAE= 则∠DAF+∠BAE=45°;(“ ”+“ ”=45°) 2. 如图①,若tan∠DFA=3,tan∠AEB=2,则∠DFA+∠AEB=135°;(“3”+“2”=135°)
3. 如图②,若tan∠AFG= ,tan∠AEB=2,!则∠AEB-∠AFG=45°;(“2”-“ ”=45°)
4. 如图③,若 tan∠DFA=3,tan∠AEH= 则∠DFA-∠AEH=45°;(“3”- “”=45°)
结论1:如图①,若 则
证明:根据网格线计算AE= ,EF= ,AF=
∴ △AEF 是等腰直角三角形,且∠AEF=90°, ∴∠DAF+∠BAE=45°.
结论2:如图①,若tan∠DFA=3,tan∠AEB=2,则.
证明:∵△AEF是等腰直角三角形, ∴∠AEB=∠EFC,
∴∠AFE=45°,∠AEF=90°,
∵∠AEB+∠FEC=90°,∠FEC+∠EFC=90°, ∴∠DFA+∠AEB=135°.
结论3:如图②,若 则
∴ ∠AEB-∠AFG = ∠DAE-∠DAF = ∠EAF=45°.
∵AD∥BC,
(结论4证明同结论3)
∴∠AEB=∠DAE,∠AFG=∠DAF,
模型拓展
拓展方向:结论中未直接给出“12345”模型
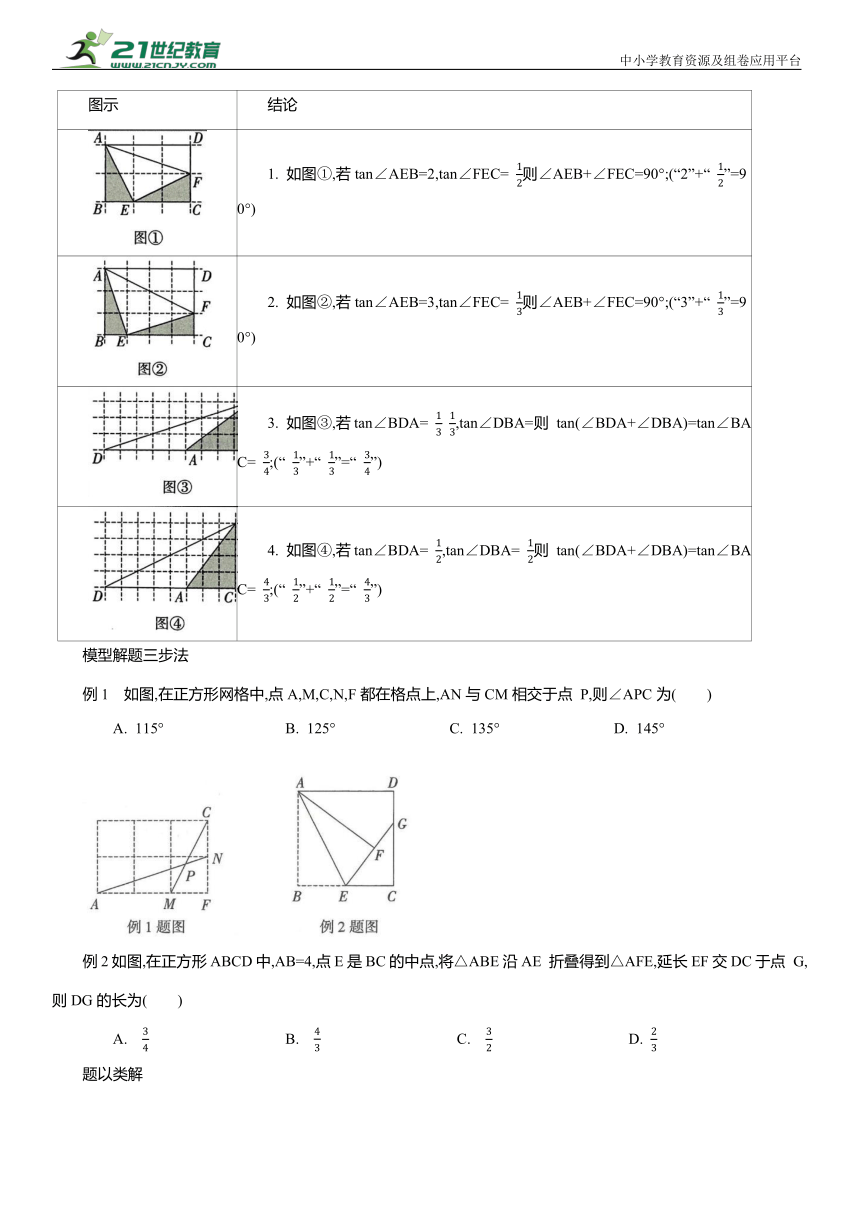
图示 结论
1. 如图①,若tan∠AEB=2,tan∠FEC= 则∠AEB+∠FEC=90°;(“2”+“ ”=90°)
2. 如图②,若tan∠AEB=3,tan∠FEC= 则∠AEB+∠FEC=90°;(“3”+“ ”=90°)
3. 如图③,若tan∠BDA= ,tan∠DBA=则 tan(∠BDA+∠DBA)=tan∠BAC= ;(“ ”+“ ”=“ ”)
4. 如图④,若tan∠BDA= ,tan∠DBA= 则 tan(∠BDA+∠DBA)=tan∠BAC= ;(“ ”+“ ”=“ ”)
模型解题三步法
例1 如图,在正方形网格中,点A,M,C,N,F都在格点上,AN与CM相交于点 P,则∠APC为( )
A. 115° B. 125° C. 135° D. 145°
例2如图,在正方形ABCD中,AB=4,点E是BC的中点,将△ABE沿AE 折叠得到△AFE,延长EF交DC于点 G,则DG的长为( )
A. B. C. D.
中小学教育资源及组卷应用平台
题以类解
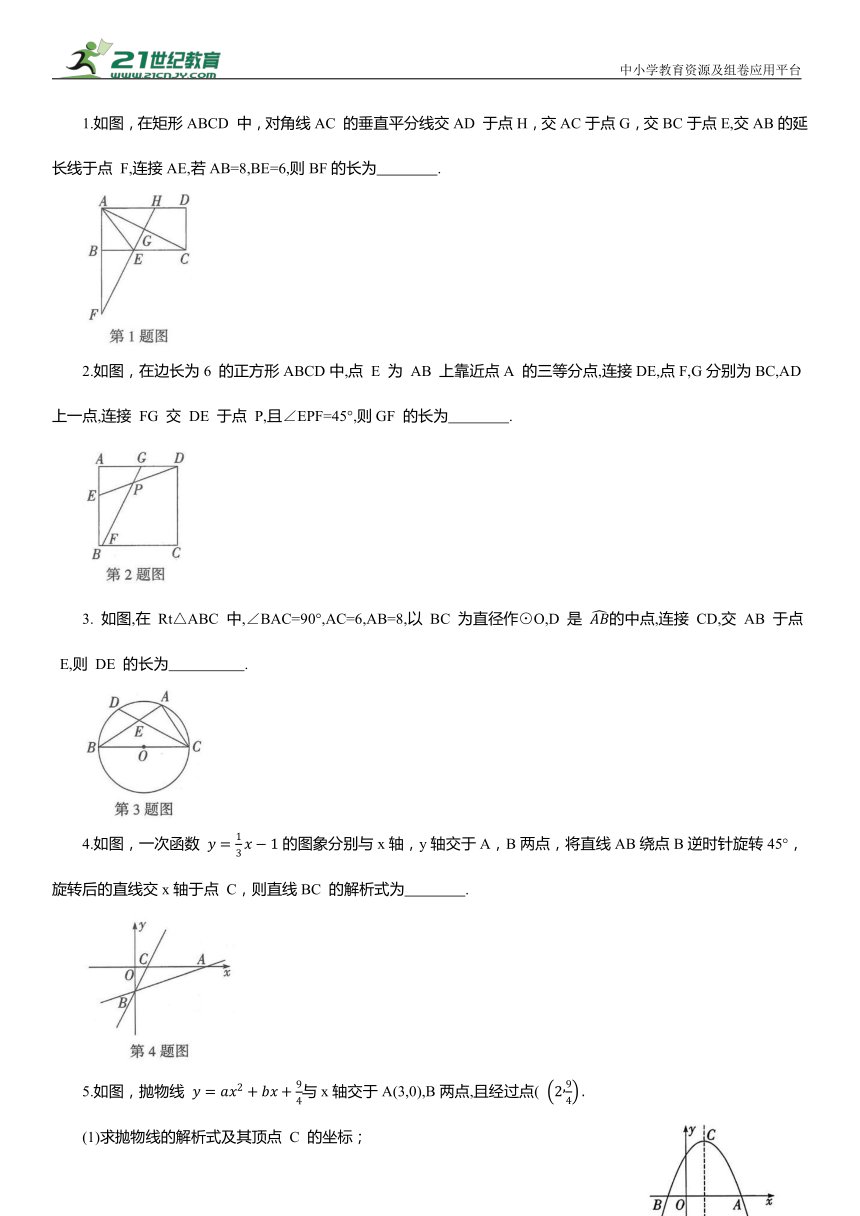
1.如图,在矩形ABCD 中,对角线AC 的垂直平分线交AD 于点H,交AC于点G,交BC于点E,交AB的延长线于点 F,连接AE,若AB=8,BE=6,则BF的长为 .
2.如图,在边长为6 的正方形ABCD中,点 E 为 AB 上靠近点A 的三等分点,连接DE,点F,G分别为BC,AD上一点,连接 FG 交 DE 于点 P,且∠EPF=45°,则GF 的长为 .
3. 如图,在 Rt△ABC 中,∠BAC=90°,AC=6,AB=8,以 BC 为直径作⊙O,D 是 的中点,连接 CD,交 AB 于点 E,则 DE 的长为 .
4.如图,一次函数 的图象分别与x轴,y轴交于A,B两点,将直线AB绕点B逆时针旋转45°,旋转后的直线交x轴于点 C,则直线BC 的解析式为 .
5.如图,抛物线 与x轴交于A(3,0),B两点,且经过点(
(1)求抛物线的解析式及其顶点 C 的坐标;
(2)设点 D 是x轴上一点,当 时,求点D 的坐标.
模型故事
为什么叫“12345”模型
何为“1,2,3”
如图,
何为“4,5”
如图,当满足 时,
对于这里的数据,为了便于记忆,通常称为“12345”模型.
模型57 “12345”模型
模型解题三步法
例1 C 【解析】找模型: 抽离模型:如解图,用模型:根据“12345”模型,得∠MCF+∠MAN =45°,∵ ∠AFC = 90°,∴ ∠APC = ∠MCF+∠MAN+∠AFC=135°.
例2 B 【解析】找模型:是否存在特殊的正切值: 抽离模型:如解图,用模型:连接AG,∵四边形ABCD 是正方形,AB=4,且点 E 是 BC 的中点,∴ BE = 2. 由折叠性质可得,AF=AB,∠AFE = ∠B = 90°,∴ AD = AF,∠ADG =∠AFG=90°. 又∵ AG=AG,∴Rt△AFG≌Rt△ADG(HL),∴∠FAG=∠DAG,∵ ∠BAE= ∠FAE, ∴ ∠BAE + ∠DAG = 45°, ∴tan∠DAG= (“12345”模型), 即DG的长为
题以类解
1.12 【解析】找模型:是否存在特殊的正切值: 抽离模型:如解图,用模型:∵ FG 垂直平分AC,∴AE=CE,∠ACE=∠EAC,∵AB=8,BE=6,∠ABC=90°,∴AE=10,∴AE=CE=10,∴BC=16,根据“12345”模型得:t =∠EGC=90°,∠BEF=∠GEC,∴ △BEF∽△GEC,∴ ∠BFE=∠GCE,∴tan∠BFE= ,∴BF=2BE=12.
2. 3 【解析】找模型:是否存在特殊角的正切值: 构造模型:如解图,过点D作DM∥GF,交BC于点M,用模型:∵DG∥FM,DM∥GF,∴四边形 DGFM 是平行四边形,∴DM=GF,又∵点 E 是AB 上靠近点A 的三等分点, (三等分点的性质),∵DM∥GF,且∠EPF=45°,∴∠EDM=45°,∴ ∠ADE+∠CDM=45°,∴ tan∠CDM= 又∵正方形 ABCD 的边长为6,∴ CM =3,∴ DM =
3. 【解析】如解图,连接OD,DB,OD 交AB于点 F,∵ 点 D 为 的中点,∴ ∠ACD =∠DCB,又∵在 Rt△ABC中, ∵ D 是 的中点, =4,OD⊥AB(垂径定理), :·AB=8,AC=6,∴BC=10,在Rt△BDC中, =∠ABD,∴在Rt△BDE中,
4. y=2x-1 【解析】如解图,分别过点 A 与点B作y轴与x轴的平行线,两平行线交于点P,根据题意可得A(3,0),B(0,-1),∴ 又∵ ∠ABC=45°,∴∠ABP+ 设直线 BC 的~~解析式为y= kx+b,将B(0,-1),C( ,0)分别代入y= kx+b,得 解得 ∴直线 BC 的解析式为y=2x-1.
5. 解:(1)把点(3,0),((2, 代入
í
∴该抛物线的解析式为 顶点 C 的坐标为(1,3);
(2)∵抛物线顶点 C(1,3),
∴抛物线的对称轴为直线x=1,
如解图,设抛物线对称轴与x轴交于点H,连接OC,AC,DC,则H(1,0),当点 D在对称轴左侧时,
在Rt△CHO中,CH=3,OH=1,
∵∠COH=∠ODC+∠DCO,
∴当∠DCO=∠CAO时,tan(∠ODC+∠CAO)=tan∠COH=3,
∵∠CAO=∠DCO,∠CDA=∠CDO,
∴△CDO∽△ADC,
设OD=a,
得
解得a=10或 (舍去),
∴D(-10,0);
当点 D 在对称轴右侧时,点D 关于直线x=1的对称点D'的坐标为(12,0),
∴点 D 的坐标为(-10,0)或(12,0).
基础模型
在如图所示的由大小相同的小正方形组成的网格内
图示 结论
1. 如图①,若tan∠DAF= ,tan∠BAE= 则∠DAF+∠BAE=45°;(“ ”+“ ”=45°) 2. 如图①,若tan∠DFA=3,tan∠AEB=2,则∠DFA+∠AEB=135°;(“3”+“2”=135°)
3. 如图②,若tan∠AFG= ,tan∠AEB=2,!则∠AEB-∠AFG=45°;(“2”-“ ”=45°)
4. 如图③,若 tan∠DFA=3,tan∠AEH= 则∠DFA-∠AEH=45°;(“3”- “”=45°)
结论1:如图①,若 则
证明:根据网格线计算AE= ,EF= ,AF=
∴ △AEF 是等腰直角三角形,且∠AEF=90°, ∴∠DAF+∠BAE=45°.
结论2:如图①,若tan∠DFA=3,tan∠AEB=2,则.
证明:∵△AEF是等腰直角三角形, ∴∠AEB=∠EFC,
∴∠AFE=45°,∠AEF=90°,
∵∠AEB+∠FEC=90°,∠FEC+∠EFC=90°, ∴∠DFA+∠AEB=135°.
结论3:如图②,若 则
∴ ∠AEB-∠AFG = ∠DAE-∠DAF = ∠EAF=45°.
∵AD∥BC,
(结论4证明同结论3)
∴∠AEB=∠DAE,∠AFG=∠DAF,
模型拓展
拓展方向:结论中未直接给出“12345”模型
图示 结论
1. 如图①,若tan∠AEB=2,tan∠FEC= 则∠AEB+∠FEC=90°;(“2”+“ ”=90°)
2. 如图②,若tan∠AEB=3,tan∠FEC= 则∠AEB+∠FEC=90°;(“3”+“ ”=90°)
3. 如图③,若tan∠BDA= ,tan∠DBA=则 tan(∠BDA+∠DBA)=tan∠BAC= ;(“ ”+“ ”=“ ”)
4. 如图④,若tan∠BDA= ,tan∠DBA= 则 tan(∠BDA+∠DBA)=tan∠BAC= ;(“ ”+“ ”=“ ”)
模型解题三步法
例1 如图,在正方形网格中,点A,M,C,N,F都在格点上,AN与CM相交于点 P,则∠APC为( )
A. 115° B. 125° C. 135° D. 145°
例2如图,在正方形ABCD中,AB=4,点E是BC的中点,将△ABE沿AE 折叠得到△AFE,延长EF交DC于点 G,则DG的长为( )
A. B. C. D.
中小学教育资源及组卷应用平台
题以类解
1.如图,在矩形ABCD 中,对角线AC 的垂直平分线交AD 于点H,交AC于点G,交BC于点E,交AB的延长线于点 F,连接AE,若AB=8,BE=6,则BF的长为 .
2.如图,在边长为6 的正方形ABCD中,点 E 为 AB 上靠近点A 的三等分点,连接DE,点F,G分别为BC,AD上一点,连接 FG 交 DE 于点 P,且∠EPF=45°,则GF 的长为 .
3. 如图,在 Rt△ABC 中,∠BAC=90°,AC=6,AB=8,以 BC 为直径作⊙O,D 是 的中点,连接 CD,交 AB 于点 E,则 DE 的长为 .
4.如图,一次函数 的图象分别与x轴,y轴交于A,B两点,将直线AB绕点B逆时针旋转45°,旋转后的直线交x轴于点 C,则直线BC 的解析式为 .
5.如图,抛物线 与x轴交于A(3,0),B两点,且经过点(
(1)求抛物线的解析式及其顶点 C 的坐标;
(2)设点 D 是x轴上一点,当 时,求点D 的坐标.
模型故事
为什么叫“12345”模型
何为“1,2,3”
如图,
何为“4,5”
如图,当满足 时,
对于这里的数据,为了便于记忆,通常称为“12345”模型.
模型57 “12345”模型
模型解题三步法
例1 C 【解析】找模型: 抽离模型:如解图,用模型:根据“12345”模型,得∠MCF+∠MAN =45°,∵ ∠AFC = 90°,∴ ∠APC = ∠MCF+∠MAN+∠AFC=135°.
例2 B 【解析】找模型:是否存在特殊的正切值: 抽离模型:如解图,用模型:连接AG,∵四边形ABCD 是正方形,AB=4,且点 E 是 BC 的中点,∴ BE = 2. 由折叠性质可得,AF=AB,∠AFE = ∠B = 90°,∴ AD = AF,∠ADG =∠AFG=90°. 又∵ AG=AG,∴Rt△AFG≌Rt△ADG(HL),∴∠FAG=∠DAG,∵ ∠BAE= ∠FAE, ∴ ∠BAE + ∠DAG = 45°, ∴tan∠DAG= (“12345”模型), 即DG的长为
题以类解
1.12 【解析】找模型:是否存在特殊的正切值: 抽离模型:如解图,用模型:∵ FG 垂直平分AC,∴AE=CE,∠ACE=∠EAC,∵AB=8,BE=6,∠ABC=90°,∴AE=10,∴AE=CE=10,∴BC=16,根据“12345”模型得:t =∠EGC=90°,∠BEF=∠GEC,∴ △BEF∽△GEC,∴ ∠BFE=∠GCE,∴tan∠BFE= ,∴BF=2BE=12.
2. 3 【解析】找模型:是否存在特殊角的正切值: 构造模型:如解图,过点D作DM∥GF,交BC于点M,用模型:∵DG∥FM,DM∥GF,∴四边形 DGFM 是平行四边形,∴DM=GF,又∵点 E 是AB 上靠近点A 的三等分点, (三等分点的性质),∵DM∥GF,且∠EPF=45°,∴∠EDM=45°,∴ ∠ADE+∠CDM=45°,∴ tan∠CDM= 又∵正方形 ABCD 的边长为6,∴ CM =3,∴ DM =
3. 【解析】如解图,连接OD,DB,OD 交AB于点 F,∵ 点 D 为 的中点,∴ ∠ACD =∠DCB,又∵在 Rt△ABC中, ∵ D 是 的中点, =4,OD⊥AB(垂径定理), :·AB=8,AC=6,∴BC=10,在Rt△BDC中, =∠ABD,∴在Rt△BDE中,
4. y=2x-1 【解析】如解图,分别过点 A 与点B作y轴与x轴的平行线,两平行线交于点P,根据题意可得A(3,0),B(0,-1),∴ 又∵ ∠ABC=45°,∴∠ABP+ 设直线 BC 的~~解析式为y= kx+b,将B(0,-1),C( ,0)分别代入y= kx+b,得 解得 ∴直线 BC 的解析式为y=2x-1.
5. 解:(1)把点(3,0),((2, 代入
í
∴该抛物线的解析式为 顶点 C 的坐标为(1,3);
(2)∵抛物线顶点 C(1,3),
∴抛物线的对称轴为直线x=1,
如解图,设抛物线对称轴与x轴交于点H,连接OC,AC,DC,则H(1,0),当点 D在对称轴左侧时,
在Rt△CHO中,CH=3,OH=1,
∵∠COH=∠ODC+∠DCO,
∴当∠DCO=∠CAO时,tan(∠ODC+∠CAO)=tan∠COH=3,
∵∠CAO=∠DCO,∠CDA=∠CDO,
∴△CDO∽△ADC,
设OD=a,
得
解得a=10或 (舍去),
∴D(-10,0);
当点 D 在对称轴右侧时,点D 关于直线x=1的对称点D'的坐标为(12,0),
∴点 D 的坐标为(-10,0)或(12,0).
同课章节目录
