模型60 阿基米德折弦定理(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型60 阿基米德折弦定理(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 337.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:35:31 | ||
图片预览


文档简介
模型60 阿基米德折弦定理
中小学教育资源及组卷应用平台
基础模型
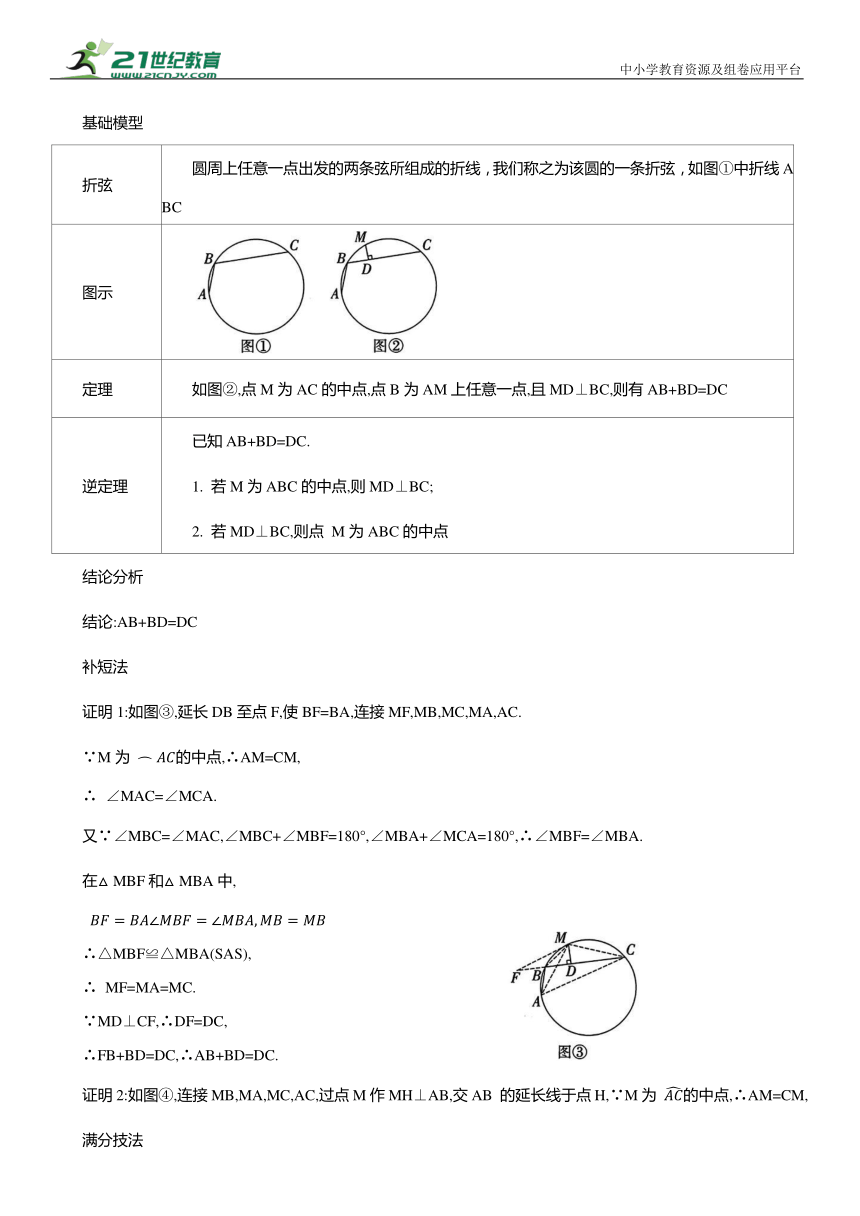
折弦 圆周上任意一点出发的两条弦所组成的折线,我们称之为该圆的一条折弦,如图①中折线ABC
图示
定理 如图②,点M为AC的中点,点B为AM上任意一点,且MD⊥BC,则有AB+BD=DC
逆定理 已知AB+BD=DC. 1. 若M为ABC的中点,则MD⊥BC; 2. 若MD⊥BC,则点 M为ABC的中点
结论分析
结论:AB+BD=DC
补短法
证明1:如图③,延长DB至点F,使BF=BA,连接MF,MB,MC,MA,AC.
∵M为 的中点,∴AM=CM,
∴ ∠MAC=∠MCA.
又∵∠MBC=∠MAC,∠MBC+∠MBF=180°,∠MBA+∠MCA=180°,∴∠MBF=∠MBA.
在△MBF和△MBA中,
∴△MBF≌△MBA(SAS),
∴ MF=MA=MC.
∵MD⊥CF,∴DF=DC,
∴FB+BD=DC,∴AB+BD=DC.
证明2:如图④,连接MB,MA,MC,AC,过点M作MH⊥AB,交AB 的延长线于点H,∵M为 的中点,∴AM=CM,
满分技法
证明线段和差关系,很重要的一个方法就是截长补短法.
补短法即:①在DB的延长线上补长度为AB 的线段 BF,只需求证 DF=DC即可.
②在AB 的延长线上构造与BD 等线段的长度BH,求证AH=DC 即可.
截长法即:在长线段 DC 上截取一条线段等于AB 或BD的长,求证剩余长度与 BD 或 AB 相等即可.
在△MHA 和△MDC中,
∴△MHA≌△MDC(AAS),∴AH=CD,MH=MD,
在Rt△MHB 和Rt△MDB中,
∴ Rt△MHB≌Rt△MDB(HL),
∴BH=BD,
又∵AH=AB+BH,AH=DC,
∴AH=AB+BD,∴AB+BD=DC.
结论:AB+BD=DC.
自主证明:请用截长法证明结论.
模型拓展
拓展方向:当点 M 在特殊位置时的考查
条件 点M为劣弧AB的中点,连接MB,MC 点M为优弧ACB的中点,连接MB,MC
图示
结论 MC -MB =AC·BC MB -MC =AC·BC
模型解题三步法
例1 如图,△ABC 内接于⊙O,已知 点 D 为 上的任意一点,连接AD,DC,∠ABD=45°,∠CBD=15°,AE⊥BD 于点E,则△BDC的周长是 .
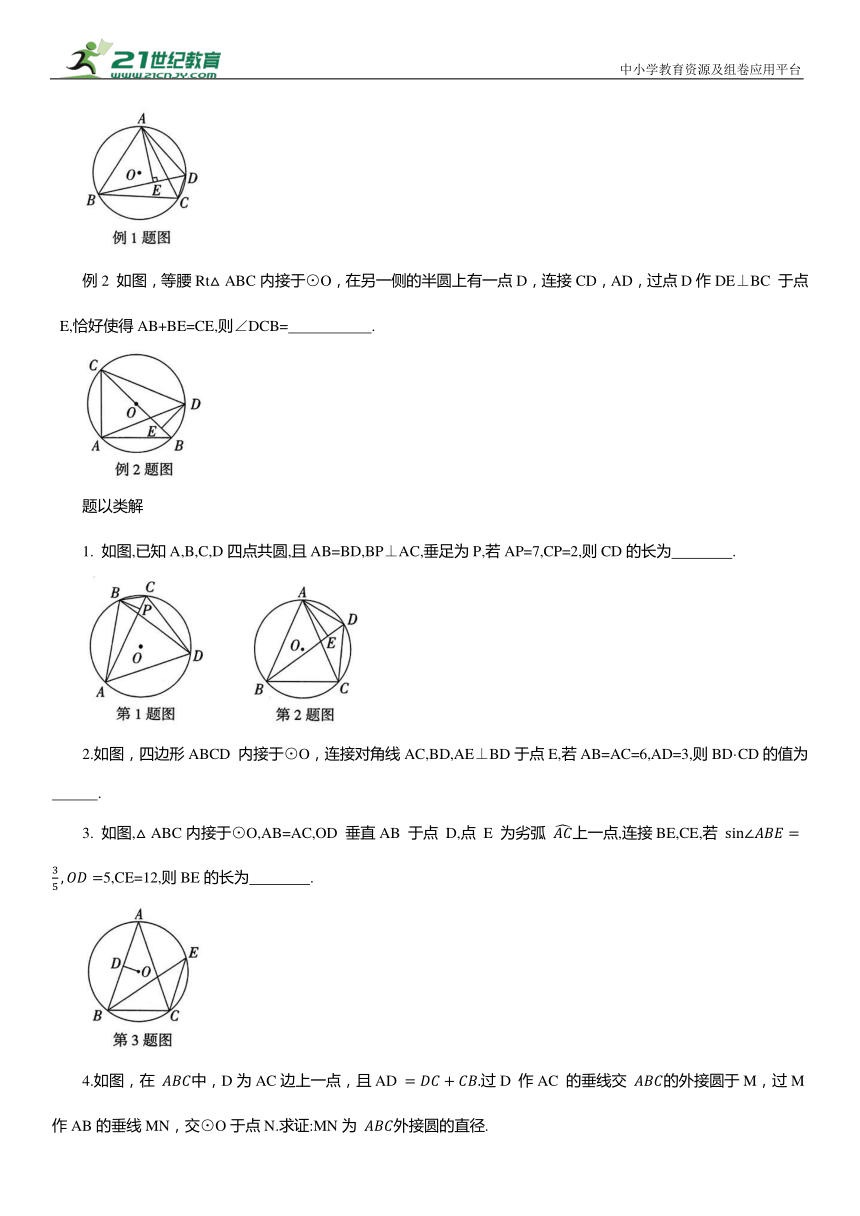
例2 如图,等腰Rt△ABC内接于⊙O,在另一侧的半圆上有一点D,连接CD,AD,过点D作DE⊥BC 于点 E,恰好使得AB+BE=CE,则∠DCB= .
题以类解
1. 如图,已知A,B,C,D四点共圆,且AB=BD,BP⊥AC,垂足为P,若AP=7,CP=2,则CD的长为 .
2.如图,四边形ABCD 内接于⊙O,连接对角线AC,BD,AE⊥BD于点E,若AB=AC=6,AD=3,则BD·CD的值为 .
3. 如图,△ABC内接于⊙O,AB=AC,OD 垂直AB 于点 D,点 E 为劣弧 上一点,连接BE,CE,若 5,CE=12,则BE的长为 .
4.如图,在 中,D为AC边上一点,且AD 过D 作AC 的垂线交 的外接圆于M,过M作AB的垂线MN,交⊙O于点N.求证:MN为 外接圆的直径.
5. 如图,在⊙O中, 点D 是优弧 上一动点(点 D 不与点 C,B 重合),连接DA,DB,DC,
(1)若 求⊙O 的半径;
(2)求证:
模型故事
阿基米德折弦定理
阿基米德是有史以来最伟大的数学家之一.他与牛顿、高斯并称为三大数学王子.
阿尔·比鲁尼的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据阿尔·比鲁尼本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.
模型展现
自主证明:截长法:
如图⑤,在 CD 上截取 DG=DB,连接 MG,MB,MC,MA,AC,
∵MD⊥BG,∴MB=MG,
∴∠MBG=∠MGB.
又∵
∴∠MBG=∠MAC,
由 M 为 中点易得
∠MAC=∠MCA,
∴∠MBG=∠MCA,
∴∠MGB=∠MCA=∠BCA+∠MCG,
而∠MGB=∠GMC+∠MCG,
∴∠GMC=∠BCA=∠BMA,
在△BMA 和△GMC中,
∴△BMA≌△GMC(SAS),
∴AB=CG,
∴AB+BD=GC+BD=GC+DG=DC.
模型解题三步法
例1 【解析】根据阿基米德折弦定理得,CD+DE=BE,∵ ∠ABD =45°,∴ BE=2 =2,∴CD+DE=2,∵∠CBD=15°,∠ABD=45°,∴∠ABC=60°,∵AB=AC,∴△ABC 是等边三角形(一个角是60°的等腰三角形是等边三角形),∴ BC=AB=AC=2 ,∴△BDC 的周长为 BE+(CD+DE)+
例2 22.5° 【解析】找模型:圆上是否存在折线:折线 ABC,折线是否存在线段关系:AB+BE=CE,是否存在垂线:DE ⊥ BC, 抽离模型:如解图,用模型:根据阿基米德折弦定理的逆定理可得点D 是优弧AC的中点,∴AD=DC,∴△ACD 是等腰三角形,又∵ △ABC是等腰直角三角形,∴ ∠ABC = ∠ACB =∠ADC=45°,∴ ∠DCA=(180°-45°)÷2=67.5°,∴∠DCB=∠DCA-∠ACB=22.5°.
题以类解
1.5 【解析】找模型:圆上是否存在折线:折线ACD,是否存在弧的中点:点B,是否过中点作垂线:BP⊥AC.抽离模型:如解图,用模型:根据阿基米德折弦定理得,AP=CP+CD,∴CD=AP-CP=7-2=5.
2.27 【解析】找模型:圆上是否存在折线:折线BDC,是否存在弧的中点:点A,是否过中点作垂线:AE⊥BD.抽离模型:如解图,用模型:根据阿基米德折弦定理得,BE=CD+DE,∵AE⊥BD,∴在 Rt△AEB中, 在 Rt△AED中,DE =AD -AE ,∴BD·CD=(BE+
3.24 【解析】如解图,连接OA,OB,AE,过点A作AF⊥BE 于点 F,∵ OD⊥AB,∴ ∠AOD= 解得EF
=6.∵AB=AC,∴点A为优弧 的中点,∵AF⊥BE,∴根据阿基米德折弦定理得,BF=EF+CE=6+12=18,∴BE=18+6=24.
4. 证明:如解图,延长AC 至点E,使CE=BC,连接MA,MB,ME,BE,
∵AD=DC+BC,∴AD=DC+CE=DE,
∵MD⊥AE,
∴MA=ME,∠MAE=∠MEA,
又∵∠MAE=∠MBC,∴∠MEC=∠MBC,
又∵CE=BC,∴∠CEB=∠CBE,
∴∠MEA+∠CEB=∠MBC+∠CBE,
即∠MEB=∠MBE,∴ME=MB,
又∵ME=MA,∴MA=MB,
又∵MN⊥AB,∴MN垂直平分AB,
∴MN是圆的直径.
5. (1)解:如解图①,连接OC,OA,BC,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠ADC=∠ABC=30°,
∴∠AOC=2∠ADC=60°,
∵OC=OA,∴△AOC 是等边三角形,
∴OA=AC=4;
(2)证明:如解图②,在 CD上截取DF=DB,过点A作AG⊥CD于点 G,连接AF
∵AC=AB,
∴∠CDA=∠BDA(等弧所对的圆周角相等),在△ABD 和△AFD中,
∴△ABD≌△AFD(SAS),
∴AF=AB=AC,∴△ACF为等腰三角形,
∵AG⊥CF,∴CG=FG,
∴DC+DB=2DG,
∵ ∠BAC = 120°,∴ ∠CDB = 180°-120°=
在 Rt△AGD 中,
中小学教育资源及组卷应用平台
基础模型
折弦 圆周上任意一点出发的两条弦所组成的折线,我们称之为该圆的一条折弦,如图①中折线ABC
图示
定理 如图②,点M为AC的中点,点B为AM上任意一点,且MD⊥BC,则有AB+BD=DC
逆定理 已知AB+BD=DC. 1. 若M为ABC的中点,则MD⊥BC; 2. 若MD⊥BC,则点 M为ABC的中点
结论分析
结论:AB+BD=DC
补短法
证明1:如图③,延长DB至点F,使BF=BA,连接MF,MB,MC,MA,AC.
∵M为 的中点,∴AM=CM,
∴ ∠MAC=∠MCA.
又∵∠MBC=∠MAC,∠MBC+∠MBF=180°,∠MBA+∠MCA=180°,∴∠MBF=∠MBA.
在△MBF和△MBA中,
∴△MBF≌△MBA(SAS),
∴ MF=MA=MC.
∵MD⊥CF,∴DF=DC,
∴FB+BD=DC,∴AB+BD=DC.
证明2:如图④,连接MB,MA,MC,AC,过点M作MH⊥AB,交AB 的延长线于点H,∵M为 的中点,∴AM=CM,
满分技法
证明线段和差关系,很重要的一个方法就是截长补短法.
补短法即:①在DB的延长线上补长度为AB 的线段 BF,只需求证 DF=DC即可.
②在AB 的延长线上构造与BD 等线段的长度BH,求证AH=DC 即可.
截长法即:在长线段 DC 上截取一条线段等于AB 或BD的长,求证剩余长度与 BD 或 AB 相等即可.
在△MHA 和△MDC中,
∴△MHA≌△MDC(AAS),∴AH=CD,MH=MD,
在Rt△MHB 和Rt△MDB中,
∴ Rt△MHB≌Rt△MDB(HL),
∴BH=BD,
又∵AH=AB+BH,AH=DC,
∴AH=AB+BD,∴AB+BD=DC.
结论:AB+BD=DC.
自主证明:请用截长法证明结论.
模型拓展
拓展方向:当点 M 在特殊位置时的考查
条件 点M为劣弧AB的中点,连接MB,MC 点M为优弧ACB的中点,连接MB,MC
图示
结论 MC -MB =AC·BC MB -MC =AC·BC
模型解题三步法
例1 如图,△ABC 内接于⊙O,已知 点 D 为 上的任意一点,连接AD,DC,∠ABD=45°,∠CBD=15°,AE⊥BD 于点E,则△BDC的周长是 .
例2 如图,等腰Rt△ABC内接于⊙O,在另一侧的半圆上有一点D,连接CD,AD,过点D作DE⊥BC 于点 E,恰好使得AB+BE=CE,则∠DCB= .
题以类解
1. 如图,已知A,B,C,D四点共圆,且AB=BD,BP⊥AC,垂足为P,若AP=7,CP=2,则CD的长为 .
2.如图,四边形ABCD 内接于⊙O,连接对角线AC,BD,AE⊥BD于点E,若AB=AC=6,AD=3,则BD·CD的值为 .
3. 如图,△ABC内接于⊙O,AB=AC,OD 垂直AB 于点 D,点 E 为劣弧 上一点,连接BE,CE,若 5,CE=12,则BE的长为 .
4.如图,在 中,D为AC边上一点,且AD 过D 作AC 的垂线交 的外接圆于M,过M作AB的垂线MN,交⊙O于点N.求证:MN为 外接圆的直径.
5. 如图,在⊙O中, 点D 是优弧 上一动点(点 D 不与点 C,B 重合),连接DA,DB,DC,
(1)若 求⊙O 的半径;
(2)求证:
模型故事
阿基米德折弦定理
阿基米德是有史以来最伟大的数学家之一.他与牛顿、高斯并称为三大数学王子.
阿尔·比鲁尼的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据阿尔·比鲁尼本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.
模型展现
自主证明:截长法:
如图⑤,在 CD 上截取 DG=DB,连接 MG,MB,MC,MA,AC,
∵MD⊥BG,∴MB=MG,
∴∠MBG=∠MGB.
又∵
∴∠MBG=∠MAC,
由 M 为 中点易得
∠MAC=∠MCA,
∴∠MBG=∠MCA,
∴∠MGB=∠MCA=∠BCA+∠MCG,
而∠MGB=∠GMC+∠MCG,
∴∠GMC=∠BCA=∠BMA,
在△BMA 和△GMC中,
∴△BMA≌△GMC(SAS),
∴AB=CG,
∴AB+BD=GC+BD=GC+DG=DC.
模型解题三步法
例1 【解析】根据阿基米德折弦定理得,CD+DE=BE,∵ ∠ABD =45°,∴ BE=2 =2,∴CD+DE=2,∵∠CBD=15°,∠ABD=45°,∴∠ABC=60°,∵AB=AC,∴△ABC 是等边三角形(一个角是60°的等腰三角形是等边三角形),∴ BC=AB=AC=2 ,∴△BDC 的周长为 BE+(CD+DE)+
例2 22.5° 【解析】找模型:圆上是否存在折线:折线 ABC,折线是否存在线段关系:AB+BE=CE,是否存在垂线:DE ⊥ BC, 抽离模型:如解图,用模型:根据阿基米德折弦定理的逆定理可得点D 是优弧AC的中点,∴AD=DC,∴△ACD 是等腰三角形,又∵ △ABC是等腰直角三角形,∴ ∠ABC = ∠ACB =∠ADC=45°,∴ ∠DCA=(180°-45°)÷2=67.5°,∴∠DCB=∠DCA-∠ACB=22.5°.
题以类解
1.5 【解析】找模型:圆上是否存在折线:折线ACD,是否存在弧的中点:点B,是否过中点作垂线:BP⊥AC.抽离模型:如解图,用模型:根据阿基米德折弦定理得,AP=CP+CD,∴CD=AP-CP=7-2=5.
2.27 【解析】找模型:圆上是否存在折线:折线BDC,是否存在弧的中点:点A,是否过中点作垂线:AE⊥BD.抽离模型:如解图,用模型:根据阿基米德折弦定理得,BE=CD+DE,∵AE⊥BD,∴在 Rt△AEB中, 在 Rt△AED中,DE =AD -AE ,∴BD·CD=(BE+
3.24 【解析】如解图,连接OA,OB,AE,过点A作AF⊥BE 于点 F,∵ OD⊥AB,∴ ∠AOD= 解得EF
=6.∵AB=AC,∴点A为优弧 的中点,∵AF⊥BE,∴根据阿基米德折弦定理得,BF=EF+CE=6+12=18,∴BE=18+6=24.
4. 证明:如解图,延长AC 至点E,使CE=BC,连接MA,MB,ME,BE,
∵AD=DC+BC,∴AD=DC+CE=DE,
∵MD⊥AE,
∴MA=ME,∠MAE=∠MEA,
又∵∠MAE=∠MBC,∴∠MEC=∠MBC,
又∵CE=BC,∴∠CEB=∠CBE,
∴∠MEA+∠CEB=∠MBC+∠CBE,
即∠MEB=∠MBE,∴ME=MB,
又∵ME=MA,∴MA=MB,
又∵MN⊥AB,∴MN垂直平分AB,
∴MN是圆的直径.
5. (1)解:如解图①,连接OC,OA,BC,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠ADC=∠ABC=30°,
∴∠AOC=2∠ADC=60°,
∵OC=OA,∴△AOC 是等边三角形,
∴OA=AC=4;
(2)证明:如解图②,在 CD上截取DF=DB,过点A作AG⊥CD于点 G,连接AF
∵AC=AB,
∴∠CDA=∠BDA(等弧所对的圆周角相等),在△ABD 和△AFD中,
∴△ABD≌△AFD(SAS),
∴AF=AB=AC,∴△ACF为等腰三角形,
∵AG⊥CF,∴CG=FG,
∴DC+DB=2DG,
∵ ∠BAC = 120°,∴ ∠CDB = 180°-120°=
在 Rt△AGD 中,
同课章节目录
