模型56 “主从联动”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型56 “主从联动”模型(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 316.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:34:31 | ||
图片预览


文档简介
模型56 “主从联动”模型
模型展现
中小学教育资源及组卷应用平台
主从联动问题变换前后的图形形状不变,但大小可能发生变化,其解题方法就是构造旋转、位似图形,本质就是对图形中的每个点进行旋转变化和位似变化
结论分析
直线轨迹结论:1. P,Q两点轨迹所在直线的夹角等于α;
2. P,Q 两点轨迹长度之比等于AP:AQ
以A,Q,P三点共线为例证明
证明:如图①,连接AB,AC,过点Q作BC的平行线,分别交AB,AC于点M,N,根据平行线分线段成比例可得
∵点 P 的轨迹为 BC,点 Q 的轨迹为 MN,
∴ P,Q两点轨迹所在直线的夹角等于0°(结论1);
P,Q两点轨迹长度之比等于AP:AQ(结论2).
注:若三点不共线,则考虑 则有
圆轨迹结论:1.两圆心与定点连线的夹角等于主、从动点与定点连线的夹角,即
2.主、从动点与定点的距离之比等于两圆心到定点的距离之比,也等于两圆半径之比,即AP:AQ
以A,Q,P三点共线为例证明
证明:如图②,连接AO,过点Q作OP 的平行线,交AO于点M,根据平行线分线段成比例可得
∵A,M,O三点共线,
∴ P,Q两点轨迹所在圆的圆心与点A 连线的夹角等于( (结论1);
主、从动点与定点的距离之比等于两圆心到定点的距离之比,也等于两圆半径之比,即 (结论2).
注:若三点不共线,则考虑 则有
模型解题三步法
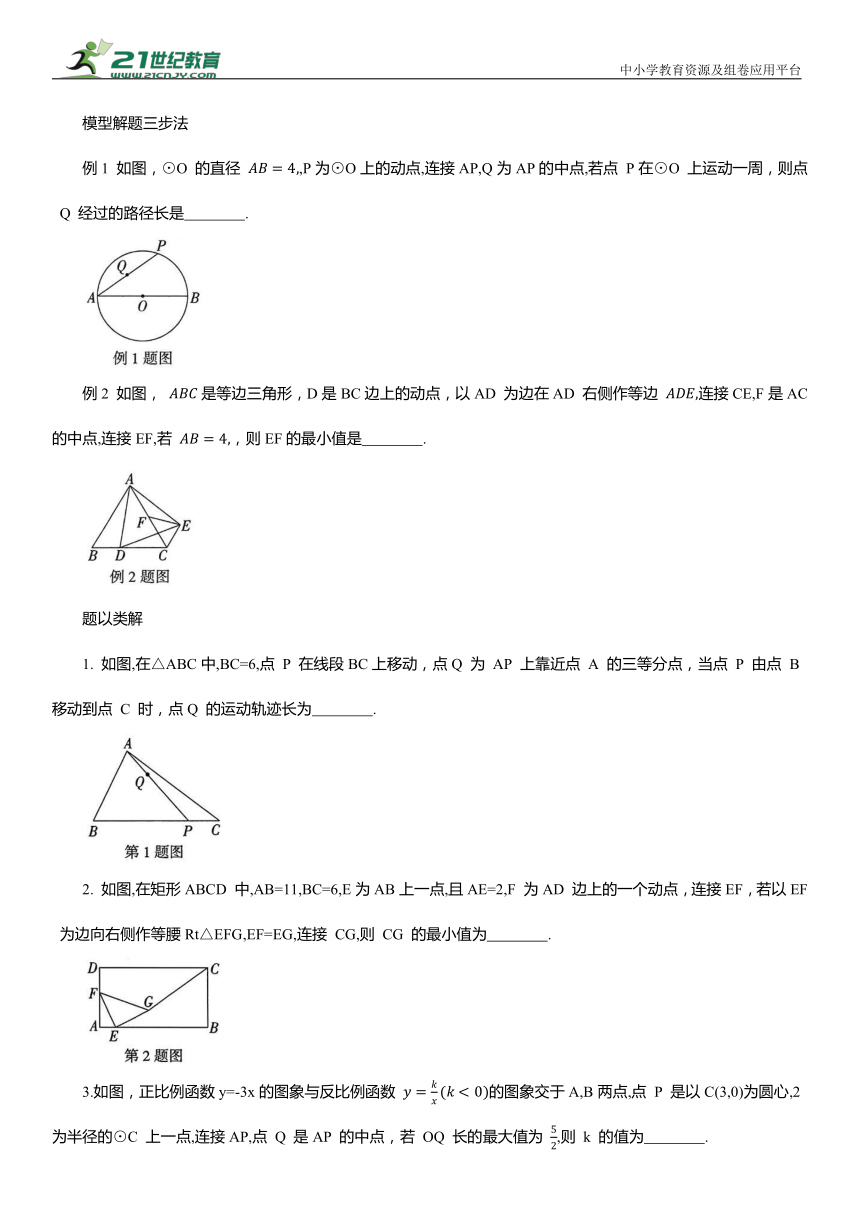
例1 如图,⊙O 的直径 ,P为⊙O上的动点,连接AP,Q为AP的中点,若点 P在⊙O 上运动一周,则点 Q 经过的路径长是 .
例2 如图, 是等边三角形,D是BC边上的动点,以AD 为边在AD 右侧作等边 连接CE,F是AC的中点,连接EF,若 ,则EF的最小值是 .
题以类解
1. 如图,在△ABC中,BC=6,点 P 在线段BC上移动,点Q 为 AP 上靠近点 A 的三等分点,当点 P 由点 B 移动到点 C 时,点Q 的运动轨迹长为 .
2. 如图,在矩形ABCD 中,AB=11,BC=6,E为AB上一点,且AE=2,F 为AD 边上的一个动点,连接EF,若以EF 为边向右侧作等腰Rt△EFG,EF=EG,连接 CG,则 CG 的最小值为 .
3.如图,正比例函数y=-3x的图象与反比例函数 的图象交于A,B两点,点 P 是以C(3,0)为圆心,2为半径的⊙C 上一点,连接AP,点 Q 是AP 的中点,若 OQ 长的最大值为 ,则 k 的值为 .
4.如图,在平面直角坐标系中,抛物线 与x轴交于A(1,0),B两点,与y轴交于点C(0,5).
(1)求抛物线的解析式;
(2)若点 P 在以点 B 为圆心,2为半径的⊙B上,⊙B与x轴交于 D,E两点(点D在点 E 左侧),连接AP,以AP 为边在 AP 下方作等腰 Rt△APQ,且. 连接EQ,求EQ长度的取值范围.
模型故事
主从联动(瓜豆模型)
“主从联动模型”也叫“瓜豆模型”,出自成语“种瓜得瓜,种豆得豆”.这类动点问题中,一个动点随另一个动点的运动而运动,我们把它们分别叫做从动点和主动点,从动点和主动点的轨迹是一致的,即所谓“种”线得线,“种”圆得圆(而当主动点轨迹是其他图形时,从动点轨迹必然也是).解决这一类问题通常用到旋转和相似.
模型解题三步法
例1 2π 【解析】如解图,连接 OQ,∵ AB=4,∴AO=2,∵ Q 为AP的中点, ∴ OQ ⊥ AP, ∴∠AQO=90°,∴点 Q 在以AO为直径的圆上运动,∴点Q 经过的路径长为2π.
例2 点D 点E 【解析】∵△ABC 和△ADE 均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE= 60°,∴ ∠BAD = ∠CAE,∴ △ABD ≌△ACE,∴ ∠ABD=∠ACE,∵ ∠ABD=60°,∴ ∠ACE = 60°,∴ 点 D 在运动过程中,∠ACE 始终等于 60°,∴点 E 的运动轨迹在射线 CE上,∵ F 为 AC 的中点,∴当 EF⊥CE时,EF的长最小,∵AC=AB=4,F为AC的中点,∴ AF = CF =2,∴ EF最小 = CF ·
题以类解
1.2 【解析】找模型:三角形边上是否存在一动点:点P(主动点),动点和定点的连线上是否存在另一动点:点Q(从动点),抽离模型:如解图,用模型:∵点 P 的运动轨迹是线段,∴点 Q 的运动轨迹是平行于 BC 的线段,如解图,过点Q作MN∥BC,交AB于点M,交AC于点N,则有: 线段MN即为点 Q 的运动轨迹.根据“主从联动”模型得: 又∵BC=6,∴MN=2,即点Q 的运动轨迹长为2.
2.5 【解析】找模型:矩形边上是否存在一动点:点F(主动点),是否存在与动点和定点连线相关的另一动点:点G(从动点),抽离模型:如解图,用模型:过点 G作 GH⊥AB 于点H,过点 G作MN∥AB,分别交AD,BC于点M,N.∵四边形ABCD 是矩形,AB=11,BC=6,∴CD=11,AD=6,∵AE=2,∴BE=9,∵∠GHE = ∠A = ∠GEF = 90°,∴ ∠GEH +∠EGH=90°,∠GEH+∠FEA=90°,∴ ∠EGH= ∠FEA,
∴ GH=AE=2,∴点 G在平行于 AB 且在AB上方到AB 距离为2 的直线 MN 上运动,
∴当点 F 与点 D 重合时,CG 有最小值,此时 即CG的最小值为5.
【解析】如解图,连接BP,由对称性得:OA=OB,∵Q是AP的中点,. 长的最大值为 ,∴BP 长的最大值为5,当 BP 过圆心 C时,BP 最长,过点 B作BD⊥x轴于点 D,∵CP=2,∴ BC=3,∵点B在直线y=-3x上,设 B(t,-3t),则CD=3-t,BD=3t,在 Rt△BCD中,由勾股定理得: 解得t=0(舍去)或 点 B 在反比例函数 的图象上,∴
4. 解:(1)将点A(1,0),C(0,5)代入 c中,
得
∴抛物线的解析式为
(2)如解图,将点 B 绕点A 顺时针旋转90°到点 B',连接AB',PB,B'Q,
∵ ∠B'AQ+∠BAQ=90°,∠PAB+∠BAQ=90°,
∴ ∠B'AQ=∠BAP,
∵AB=AB',AP=AQ,
∴△AQB'≌△APB(SAS),∴BP=B'Q,
∵PB=2,∴B'Q=2,
∴点 Q 在以点 B'为圆心,2为半径的圆上运动,
由(1)得B(5,0),A(1,0),
∴ B'(1,-4),AB'=4,
∵BE=2,∴点E(7,0),AE=6,
∴ EQ 的 最 大 值 为 最小值为
模型展现
中小学教育资源及组卷应用平台
主从联动问题变换前后的图形形状不变,但大小可能发生变化,其解题方法就是构造旋转、位似图形,本质就是对图形中的每个点进行旋转变化和位似变化
结论分析
直线轨迹结论:1. P,Q两点轨迹所在直线的夹角等于α;
2. P,Q 两点轨迹长度之比等于AP:AQ
以A,Q,P三点共线为例证明
证明:如图①,连接AB,AC,过点Q作BC的平行线,分别交AB,AC于点M,N,根据平行线分线段成比例可得
∵点 P 的轨迹为 BC,点 Q 的轨迹为 MN,
∴ P,Q两点轨迹所在直线的夹角等于0°(结论1);
P,Q两点轨迹长度之比等于AP:AQ(结论2).
注:若三点不共线,则考虑 则有
圆轨迹结论:1.两圆心与定点连线的夹角等于主、从动点与定点连线的夹角,即
2.主、从动点与定点的距离之比等于两圆心到定点的距离之比,也等于两圆半径之比,即AP:AQ
以A,Q,P三点共线为例证明
证明:如图②,连接AO,过点Q作OP 的平行线,交AO于点M,根据平行线分线段成比例可得
∵A,M,O三点共线,
∴ P,Q两点轨迹所在圆的圆心与点A 连线的夹角等于( (结论1);
主、从动点与定点的距离之比等于两圆心到定点的距离之比,也等于两圆半径之比,即 (结论2).
注:若三点不共线,则考虑 则有
模型解题三步法
例1 如图,⊙O 的直径 ,P为⊙O上的动点,连接AP,Q为AP的中点,若点 P在⊙O 上运动一周,则点 Q 经过的路径长是 .
例2 如图, 是等边三角形,D是BC边上的动点,以AD 为边在AD 右侧作等边 连接CE,F是AC的中点,连接EF,若 ,则EF的最小值是 .
题以类解
1. 如图,在△ABC中,BC=6,点 P 在线段BC上移动,点Q 为 AP 上靠近点 A 的三等分点,当点 P 由点 B 移动到点 C 时,点Q 的运动轨迹长为 .
2. 如图,在矩形ABCD 中,AB=11,BC=6,E为AB上一点,且AE=2,F 为AD 边上的一个动点,连接EF,若以EF 为边向右侧作等腰Rt△EFG,EF=EG,连接 CG,则 CG 的最小值为 .
3.如图,正比例函数y=-3x的图象与反比例函数 的图象交于A,B两点,点 P 是以C(3,0)为圆心,2为半径的⊙C 上一点,连接AP,点 Q 是AP 的中点,若 OQ 长的最大值为 ,则 k 的值为 .
4.如图,在平面直角坐标系中,抛物线 与x轴交于A(1,0),B两点,与y轴交于点C(0,5).
(1)求抛物线的解析式;
(2)若点 P 在以点 B 为圆心,2为半径的⊙B上,⊙B与x轴交于 D,E两点(点D在点 E 左侧),连接AP,以AP 为边在 AP 下方作等腰 Rt△APQ,且. 连接EQ,求EQ长度的取值范围.
模型故事
主从联动(瓜豆模型)
“主从联动模型”也叫“瓜豆模型”,出自成语“种瓜得瓜,种豆得豆”.这类动点问题中,一个动点随另一个动点的运动而运动,我们把它们分别叫做从动点和主动点,从动点和主动点的轨迹是一致的,即所谓“种”线得线,“种”圆得圆(而当主动点轨迹是其他图形时,从动点轨迹必然也是).解决这一类问题通常用到旋转和相似.
模型解题三步法
例1 2π 【解析】如解图,连接 OQ,∵ AB=4,∴AO=2,∵ Q 为AP的中点, ∴ OQ ⊥ AP, ∴∠AQO=90°,∴点 Q 在以AO为直径的圆上运动,∴点Q 经过的路径长为2π.
例2 点D 点E 【解析】∵△ABC 和△ADE 均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE= 60°,∴ ∠BAD = ∠CAE,∴ △ABD ≌△ACE,∴ ∠ABD=∠ACE,∵ ∠ABD=60°,∴ ∠ACE = 60°,∴ 点 D 在运动过程中,∠ACE 始终等于 60°,∴点 E 的运动轨迹在射线 CE上,∵ F 为 AC 的中点,∴当 EF⊥CE时,EF的长最小,∵AC=AB=4,F为AC的中点,∴ AF = CF =2,∴ EF最小 = CF ·
题以类解
1.2 【解析】找模型:三角形边上是否存在一动点:点P(主动点),动点和定点的连线上是否存在另一动点:点Q(从动点),抽离模型:如解图,用模型:∵点 P 的运动轨迹是线段,∴点 Q 的运动轨迹是平行于 BC 的线段,如解图,过点Q作MN∥BC,交AB于点M,交AC于点N,则有: 线段MN即为点 Q 的运动轨迹.根据“主从联动”模型得: 又∵BC=6,∴MN=2,即点Q 的运动轨迹长为2.
2.5 【解析】找模型:矩形边上是否存在一动点:点F(主动点),是否存在与动点和定点连线相关的另一动点:点G(从动点),抽离模型:如解图,用模型:过点 G作 GH⊥AB 于点H,过点 G作MN∥AB,分别交AD,BC于点M,N.∵四边形ABCD 是矩形,AB=11,BC=6,∴CD=11,AD=6,∵AE=2,∴BE=9,∵∠GHE = ∠A = ∠GEF = 90°,∴ ∠GEH +∠EGH=90°,∠GEH+∠FEA=90°,∴ ∠EGH= ∠FEA,
∴ GH=AE=2,∴点 G在平行于 AB 且在AB上方到AB 距离为2 的直线 MN 上运动,
∴当点 F 与点 D 重合时,CG 有最小值,此时 即CG的最小值为5.
【解析】如解图,连接BP,由对称性得:OA=OB,∵Q是AP的中点,. 长的最大值为 ,∴BP 长的最大值为5,当 BP 过圆心 C时,BP 最长,过点 B作BD⊥x轴于点 D,∵CP=2,∴ BC=3,∵点B在直线y=-3x上,设 B(t,-3t),则CD=3-t,BD=3t,在 Rt△BCD中,由勾股定理得: 解得t=0(舍去)或 点 B 在反比例函数 的图象上,∴
4. 解:(1)将点A(1,0),C(0,5)代入 c中,
得
∴抛物线的解析式为
(2)如解图,将点 B 绕点A 顺时针旋转90°到点 B',连接AB',PB,B'Q,
∵ ∠B'AQ+∠BAQ=90°,∠PAB+∠BAQ=90°,
∴ ∠B'AQ=∠BAP,
∵AB=AB',AP=AQ,
∴△AQB'≌△APB(SAS),∴BP=B'Q,
∵PB=2,∴B'Q=2,
∴点 Q 在以点 B'为圆心,2为半径的圆上运动,
由(1)得B(5,0),A(1,0),
∴ B'(1,-4),AB'=4,
∵BE=2,∴点E(7,0),AE=6,
∴ EQ 的 最 大 值 为 最小值为
同课章节目录
