模型47 “8字”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型47 “8字”模型(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 285.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:33:58 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
模型47 “8字”模型
基础模型
结论分析
结论:△AOB∽△COD
证明:∵AB∥CD,∴∠OAB=∠OCD,
∵∠AOB=∠COD,∴ △AOB∽△COD.
模型拓展
拓展方向:由正“8字”型向斜“8字”型拓展
类型 斜“8字”型(蝴蝶型) 斜“8字”型(燕尾型)
图示
条件 AC 与BD 交于点 O,∠A=∠D(或∠B=∠C) B,D 分别是边AE,CE上一点,AD 与 BC 相交于点F,∠A=∠C(或∠ABF=∠CDF)
结论 △AOB∽△DOC △ABF∽△CDF
模型解题三步法
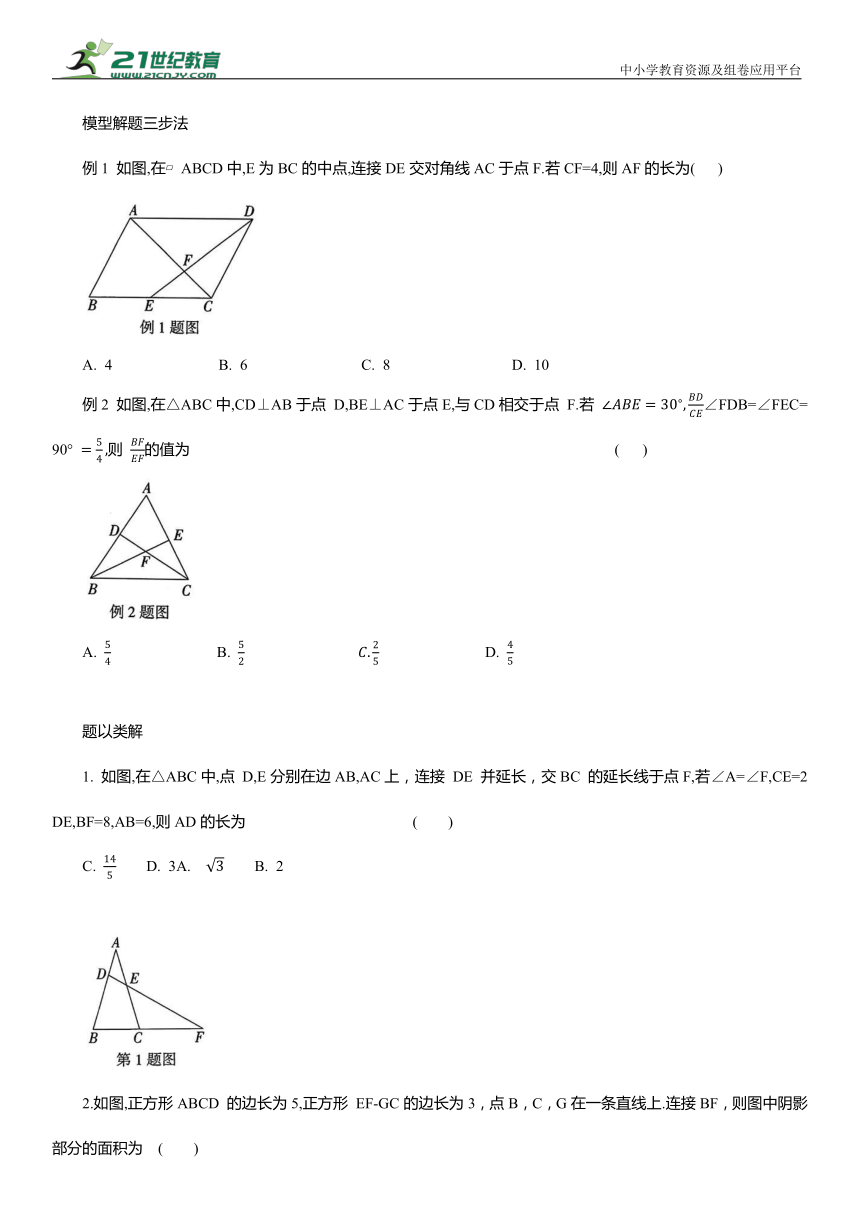
例1 如图,在 ABCD中,E为BC的中点,连接DE交对角线AC于点F.若CF=4,则AF的长为( )
A. 4 B. 6 C. 8 D. 10
例2 如图,在△ABC中,CD⊥AB于点 D,BE⊥AC于点E,与CD相交于点 F.若 ∠FDB=∠FEC=90° 则 的值为 ( )
A. B. D.
题以类解
1. 如图,在△ABC中,点 D,E分别在边AB,AC上,连接 DE 并延长,交BC 的延长线于点F,若∠A=∠F,CE=2DE,BF=8,AB=6,则AD的长为 ( )
C. D. 3A. B. 2
2.如图,正方形ABCD 的边长为5,正方形 EF-GC的边长为3,点B,C,G在一条直线上.连接BF,则图中阴影部分的面积为 ( )
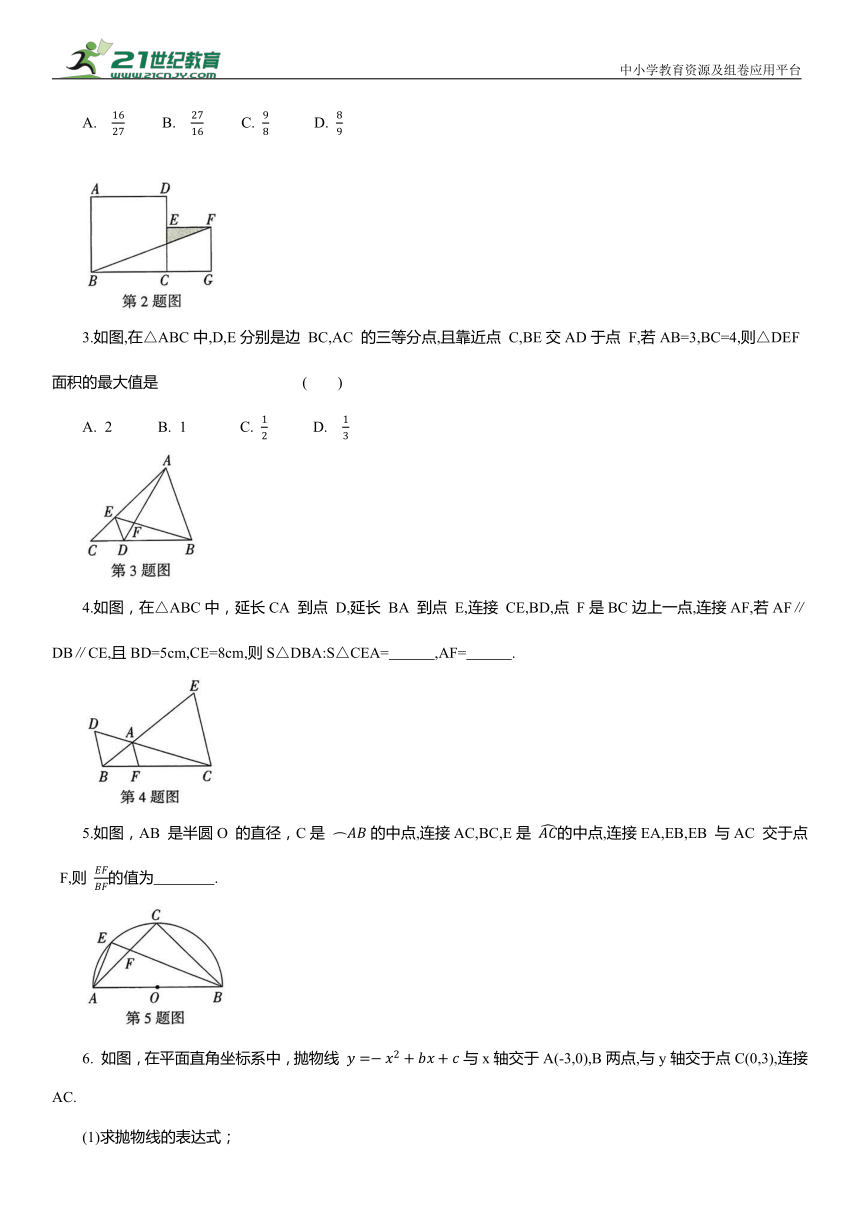
A. B. C. D.
3.如图,在△ABC中,D,E分别是边 BC,AC 的三等分点,且靠近点 C,BE交AD于点 F,若AB=3,BC=4,则△DEF面积的最大值是 ( )
A. 2 B. 1 C. D.
4.如图,在△ABC中,延长CA 到点 D,延长 BA 到点 E,连接 CE,BD,点 F是BC边上一点,连接AF,若AF∥DB∥CE,且BD=5cm,CE=8cm,则S△DBA:S△CEA= ,AF= .
5.如图,AB 是半圆O 的直径,C是 的中点,连接AC,BC,E是 的中点,连接EA,EB,EB 与AC 交于点 F,则 的值为 .
6. 如图,在平面直角坐标系中,抛物线 与x轴交于A(-3,0),B两点,与y轴交于点C(0,3),连接AC.
(1)求抛物线的表达式;
(2)点D 是直线AC 上方抛物线上一点,连接OD,CD,OD 交AC 于点 F,若 3:2,求点 D 的坐标.
模型解题三步法
例1 C 【解析】找模型:对顶角:是否存在含对顶角的两个三角形:△AFD 和△CFE,平行:这两个三角形中是否存在平行关系:AD∥CE,抽离模型:如解图,用模型:∵E 是边BC的中点 ∵四边形ABCD 是平行四边形,∴AD∥BC,AD=BC,∴CE= AD,根据正“8字”模型可得:△CFE∽△AFD,∴
例2 B 【解析】找模型:对顶角:是否存在含对顶角的两个三角形:△BDF 和△CEF,等角:这两个三角形中是否存在其他相等的角:∠FDB=∠FEC,抽离模型:如解图,用模型:∵ CD ⊥AB,BE⊥AC,∴ ∠BDF =∠CEF=90°,根据斜“8字”模型得:△DFB∽△EFC,∴∠DBF=∠ECF=30°,BD=BFCF 在 Rt△ECF 中,∠ECF=30°,∴ EF=
题以类解
1. C 【解析】找模型:是否存在含对顶角的两个三角形:△ADE 和△FCE.在这两个三角形中是否存在其他相等的角:∠A=∠F.抽离模型:如解图,用模型:根据斜“8字”模型可得:
∠A=∠F,∠B=∠B,∴△BFD∽△BAC,∴ 设AD=x,则CF=2x,∴BD=AB-AD=6-x,BC=BF-
2. B 【解析】找模型:是否存在含对顶角的两三角形:△EFH 和△CBH.在这两个三角形中是否存在平行关系. EF∥CB.抽离模型:如解图,设BF与CE交于点 H,用模型:根据正“8字”模型可得:
3. D 【解析】∵D,E分别是边 BC,AC 的三等分点,∴ “A字”模型), ∴DE∥AB,∴ △DEF∽△ABF(正“8字”模型) ∴当 S△ABD 最大时,S△DEF最大,当 AB⊥BD 时,S△ABD 取得最大值,
4. 25:64; 【解析】∵ DB∥CE,∴ ∠D =∠ACE,∵ ∠DAB=∠CAE,∴ △DAB∽△CAE(正“8字”模型), 25:64;∵AF∥CE,∴AFE=FBC①(正“A”字模型),同理可得 (正“A”字模型),①
【解析】如解图,连接 OE 交 AC 于点 H,∵E是 的中点,∴OE⊥AC,∵AB 是半圆O 的直径,∴ BC ⊥AC,∴ OE∥BC,∴ △EHF∽△BCF(正“8字”模型), 设BC=x,则
6. 解:(1)∵抛物线 与x轴交于A(-3,0),B两点,与y轴交于点 C(0,3),
∴将A(-3,0),C(0,3)代入 得 解得
∴抛物线的表达式为
(2)如解图,过点 D 作 DG∥y轴交AC 于点 G,∵S△COF:S△CDF=3:2,
∴OF:DF=3:2,
∵ DG ∥OC,∴ ∠OCF = ∠CGD, ∠COF=∠ODG,
∴△COF∽△GDF(正“8字”模型),
∵OC=3,∴DG=2,
易得直线AC 的解析式为y=x+3,
设点 D 的坐标为((m,-m
-2m+3),则点 G 的坐标
为(m,m+3),
其中-3解得
∴点D 的坐标为(-1,4)或(-2,3).
模型47 “8字”模型
基础模型
结论分析
结论:△AOB∽△COD
证明:∵AB∥CD,∴∠OAB=∠OCD,
∵∠AOB=∠COD,∴ △AOB∽△COD.
模型拓展
拓展方向:由正“8字”型向斜“8字”型拓展
类型 斜“8字”型(蝴蝶型) 斜“8字”型(燕尾型)
图示
条件 AC 与BD 交于点 O,∠A=∠D(或∠B=∠C) B,D 分别是边AE,CE上一点,AD 与 BC 相交于点F,∠A=∠C(或∠ABF=∠CDF)
结论 △AOB∽△DOC △ABF∽△CDF
模型解题三步法
例1 如图,在 ABCD中,E为BC的中点,连接DE交对角线AC于点F.若CF=4,则AF的长为( )
A. 4 B. 6 C. 8 D. 10
例2 如图,在△ABC中,CD⊥AB于点 D,BE⊥AC于点E,与CD相交于点 F.若 ∠FDB=∠FEC=90° 则 的值为 ( )
A. B. D.
题以类解
1. 如图,在△ABC中,点 D,E分别在边AB,AC上,连接 DE 并延长,交BC 的延长线于点F,若∠A=∠F,CE=2DE,BF=8,AB=6,则AD的长为 ( )
C. D. 3A. B. 2
2.如图,正方形ABCD 的边长为5,正方形 EF-GC的边长为3,点B,C,G在一条直线上.连接BF,则图中阴影部分的面积为 ( )
A. B. C. D.
3.如图,在△ABC中,D,E分别是边 BC,AC 的三等分点,且靠近点 C,BE交AD于点 F,若AB=3,BC=4,则△DEF面积的最大值是 ( )
A. 2 B. 1 C. D.
4.如图,在△ABC中,延长CA 到点 D,延长 BA 到点 E,连接 CE,BD,点 F是BC边上一点,连接AF,若AF∥DB∥CE,且BD=5cm,CE=8cm,则S△DBA:S△CEA= ,AF= .
5.如图,AB 是半圆O 的直径,C是 的中点,连接AC,BC,E是 的中点,连接EA,EB,EB 与AC 交于点 F,则 的值为 .
6. 如图,在平面直角坐标系中,抛物线 与x轴交于A(-3,0),B两点,与y轴交于点C(0,3),连接AC.
(1)求抛物线的表达式;
(2)点D 是直线AC 上方抛物线上一点,连接OD,CD,OD 交AC 于点 F,若 3:2,求点 D 的坐标.
模型解题三步法
例1 C 【解析】找模型:对顶角:是否存在含对顶角的两个三角形:△AFD 和△CFE,平行:这两个三角形中是否存在平行关系:AD∥CE,抽离模型:如解图,用模型:∵E 是边BC的中点 ∵四边形ABCD 是平行四边形,∴AD∥BC,AD=BC,∴CE= AD,根据正“8字”模型可得:△CFE∽△AFD,∴
例2 B 【解析】找模型:对顶角:是否存在含对顶角的两个三角形:△BDF 和△CEF,等角:这两个三角形中是否存在其他相等的角:∠FDB=∠FEC,抽离模型:如解图,用模型:∵ CD ⊥AB,BE⊥AC,∴ ∠BDF =∠CEF=90°,根据斜“8字”模型得:△DFB∽△EFC,∴∠DBF=∠ECF=30°,BD=BFCF 在 Rt△ECF 中,∠ECF=30°,∴ EF=
题以类解
1. C 【解析】找模型:是否存在含对顶角的两个三角形:△ADE 和△FCE.在这两个三角形中是否存在其他相等的角:∠A=∠F.抽离模型:如解图,用模型:根据斜“8字”模型可得:
∠A=∠F,∠B=∠B,∴△BFD∽△BAC,∴ 设AD=x,则CF=2x,∴BD=AB-AD=6-x,BC=BF-
2. B 【解析】找模型:是否存在含对顶角的两三角形:△EFH 和△CBH.在这两个三角形中是否存在平行关系. EF∥CB.抽离模型:如解图,设BF与CE交于点 H,用模型:根据正“8字”模型可得:
3. D 【解析】∵D,E分别是边 BC,AC 的三等分点,∴ “A字”模型), ∴DE∥AB,∴ △DEF∽△ABF(正“8字”模型) ∴当 S△ABD 最大时,S△DEF最大,当 AB⊥BD 时,S△ABD 取得最大值,
4. 25:64; 【解析】∵ DB∥CE,∴ ∠D =∠ACE,∵ ∠DAB=∠CAE,∴ △DAB∽△CAE(正“8字”模型), 25:64;∵AF∥CE,∴AFE=FBC①(正“A”字模型),同理可得 (正“A”字模型),①
【解析】如解图,连接 OE 交 AC 于点 H,∵E是 的中点,∴OE⊥AC,∵AB 是半圆O 的直径,∴ BC ⊥AC,∴ OE∥BC,∴ △EHF∽△BCF(正“8字”模型), 设BC=x,则
6. 解:(1)∵抛物线 与x轴交于A(-3,0),B两点,与y轴交于点 C(0,3),
∴将A(-3,0),C(0,3)代入 得 解得
∴抛物线的表达式为
(2)如解图,过点 D 作 DG∥y轴交AC 于点 G,∵S△COF:S△CDF=3:2,
∴OF:DF=3:2,
∵ DG ∥OC,∴ ∠OCF = ∠CGD, ∠COF=∠ODG,
∴△COF∽△GDF(正“8字”模型),
∵OC=3,∴DG=2,
易得直线AC 的解析式为y=x+3,
设点 D 的坐标为((m,-m
-2m+3),则点 G 的坐标
为(m,m+3),
其中-3
∴点D 的坐标为(-1,4)或(-2,3).
同课章节目录
