模型58 “海盗埋宝”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型58 “海盗埋宝”模型(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 299.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:33:06 | ||
图片预览



文档简介
模型58 “海盗埋宝”模型
模型展现
图示
条件 △ACD和△BEC是等腰直角三角形,A,B为直角顶点,且C点为公共点,连接DE,F 为DE的中点,连接FA,FB,AB
作法 延长AF至点 P,使得FP=AF,连接PE,PB,延长PE交AC于点 Q
结论 1. △DAF≌△EPF(SAS); 2. △ACB≌△PEB(SAS); 3.△ABP 是等腰直角三角形; 4.△FAB 是等腰直角三角形
结论分析
结论:1. △DAF≌△EPF(SAS);2. △ACB≌△PEB(SAS);
3. △ABP 是等腰直角三角形;4. △FAB 是等腰直角三角形
证明:如图,延长AF至点P,使得FP=AF,连接PE,PB,延长PE交AC 于点Q.
∵F为DE的中点,∴DF=EF.
在△DAF和△EPF中,
∴ △DAF≌△EPF(SAS)(结论1),
∴DA=EP,∠DAF=∠EPF,
∴DA∥PQ,
∴∠EQC=∠DAQ=90°.
在四边形 EQCB 中,∠EQC+∠EBC=90°+90°=180°,
∴∠QEB+∠QCB=180°.
又∵∠QEB+∠PEB=180°,
∴∠QCB=∠PEB.
∵△ACD 和△BEC 为等腰直角三角形,∴ AD=AC,BE=BC,∴AC=PE.
在△ACB 和△PEB中,
∴△ACB≌△PEB(SAS)(结论2),
∴AB=PB,∠ABC=∠PBE,
∴∠ABC+∠ABE=∠PBE+∠ABE,即∠CBE=∠ABP=90°,
∴ △ABP 是等腰直角三角形(结论3).
又∵F是AP 的中点,
∴BF⊥AP,BF=AF,
∴△FAB 是等腰直角三角形(结论4).
模型解题三步法
例 如图,在△ABC 中,分别以AC 和AB 为斜边,向△ABC 的内侧作等腰 Rt△AEC 和等腰Rt△ADB,F是BC的中点,连接FD,FE,DE,若FD=4,则线段DE的长为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,在△ABC中,∠ACB=90°,BC=AC,在等腰直角△BDE 中,∠BDE=90°,若 F 是AE的中点,则∠DFC 的度数为 ( )
A. 60° B. 90° C. 120° D. 150°
2. 如图,在等腰△ABC中,AB=AC,分别以AB,AC为斜边向△ABC的外侧作等腰 Rt△ADB和等腰 Rt△AEC,分别过点 D,E 作 DF⊥AB于点F,EG⊥AC 于点 G,若 M 是 BC 的中点,连接MD,ME,FM,GM,则下列结论不正确的是 ( )
A. BF=CG
B. MD=ME
C. △DFM 和△EGM 都是等腰三角形
D.四边形AFMG不是菱形
3.如图,在等腰Rt△ABC中,∠ABC=90°,延长BC 到点 E,以CE 为斜边,在 CE 下方作等腰Rt△CDE,连接 BD,AE,F 为 AE的中点,连接BF,DF.若AB=2,CD=3 ,则BF的长为 ,△BFD的面积为 .
4.如图,等腰 Rt△ABC 和等腰Rt△BDE有公共顶点 B,∠BAC=∠BDE=90°,连接CE,F是CE的中点,连接FA,FD.
(1)如图①,若D,A,B 三点共线,求证:AF∥BE;
(2)如图②,当∠ABD=45°,DF=4时,求AF的长.
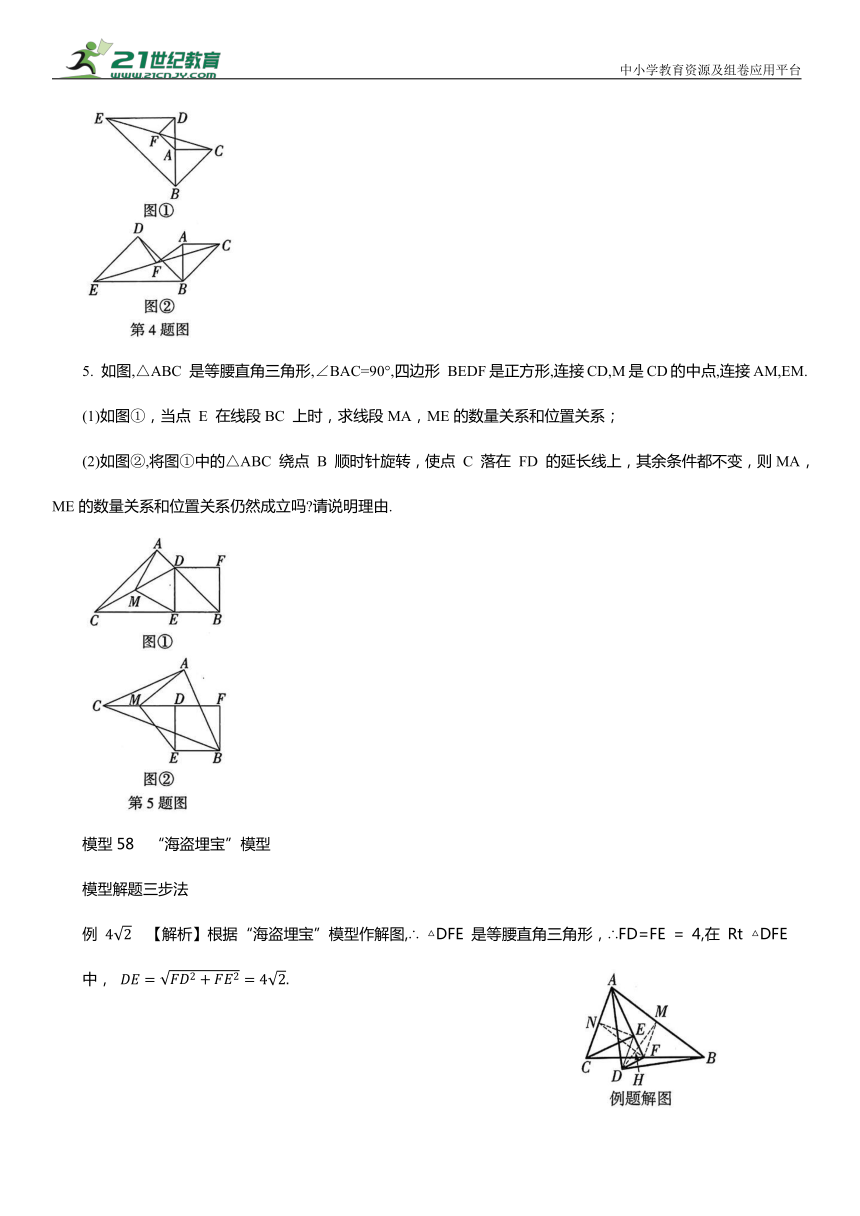
5. 如图,△ABC 是等腰直角三角形,∠BAC=90°,四边形 BEDF是正方形,连接CD,M是CD的中点,连接AM,EM.
(1)如图①,当点 E 在线段BC 上时,求线段MA,ME的数量关系和位置关系;
(2)如图②,将图①中的△ABC 绕点 B 顺时针旋转,使点 C 落在 FD 的延长线上,其余条件都不变,则MA,ME的数量关系和位置关系仍然成立吗 请说明理由.
模型58 “海盗埋宝”模型
模型解题三步法
例 【解析】根据“海盗埋宝”模型作解图,∴ △DFE 是等腰直角三角形,∴FD=FE = 4,在 Rt △DFE
中,
题以类解
1. B 【解析】找模型:是否存在两个等腰直角三角形共底角顶点:△BDE 和△ABC,共顶点:点B,是否存在另一组底角顶点连线的中点:点F.抽离模型:如解图,用模型:根据“海盗埋宝”模型得,DF⊥CF,∴∠DFC=90°.
2. D 【解析】找模型:是否存在两个等腰直角三角形共底角顶点:△ADB 和△AEC,共顶点:点A,是否存在另一组底角顶点连线的中点:点M.抽离模型:如解图,用模型:根据“海盗埋宝”模型,得△DBM≌△ECM,∴ MD=ME,故B 选项正确,不符合题意;∵△ADB 和△AEC 是等腰直角三角形,∴∠ABD=∠DAB=∠ACE=∠EAC=45°,∠ADB=∠AEC=90°,在△ADB 和△AEC 中,△ADB≌△AEC(AAS),∴ BD=CE,AD=AE,∵DF⊥AB 于点 F,EG⊥AC 于点 G,∴DF= CG,故A 选项正确,不符合题意;∵F,M,G分别是AB,BC,AC的中点,∴MF,MG 是△ABC的中位线, 和△EGM都是等腰三角形,故C 选项正确,不符合题意;如解图,连接AM,∵AB=AC,M 是BC的中点,∴AM⊥BC,∴∠AMB=∠AMC= 90°,又∵ GM= AC=AG,∴AF=FM=GM=AG,∴四边形AFMG是菱形,故D 选项错误,符合题意.
【解析】∵AB=2,CD=3 ,∴BC=AB=2,CE= CD=6,∴BE=BC+CE=8,∴ ∵点F 是AE 的中点,∴ (直角三角形斜边中线等于斜边一半),由“海盗埋宝”模型知,△BFD 是等腰直角三角形,∴
4. (1)证明:如解图①,延长AF交DE于点M,∵∠CAD=∠BAC=∠BDE=90°,∴AC∥DE,∴∠ACF=∠MEF,
∵F为CE的中点,∴CF=EF,在△ACF和△MEF中,
∴△ACF≌△MEF(ASA),
∴AC=EM,AF=MF,
∵ △ABC 和△BDE是等腰直角三角形,
∴AB=AC,BD=DE,∠DEB=45°,
∵EM=AC=BA,
∴BD-AB=DE-EM,∴AD=DM,
又∵∠ADM=90°,∴∠DMA=45°=∠DEB,
∴AF∥BE;
(2)解:如解图②,延长CA 交 BD 于点 P,连接 PE,延长 ED与BA 的延长线交于点 G,连接CG,
∵△ABC是等腰直角三角形,
∴AB=AC,∠ABC=∠ACB=45°,∠BAC=90°,
∵∠ABD=45°,
∴∠APB=45°=∠ABD=∠ACB,
∴AB=AP,BC=BP,
∴AC=AP(等腰三角形“三线合一”),
∵F为CE的中点,
(中位线的性质).
同理可得
在△BCG和△BPE中,
∴△BCG≌△BPE(SAS)(“海盗埋宝”模型),
∴CG=PE,
∴AF=DF=4.
5. 解:(1)在△ACD中,
∵M是CD的中点,∠BAC=90°,
∴ ∠MAC=∠MCA.
∵四边形 BEDF 是正方形,
∴∠DEC=90°.
在△DEC中,∵M是CD的中点,
∴MA=ME,
∵∠MCA+∠MCE=∠ACB=45°,
∴ ∠AME=∠MAC+∠MCA+∠MCE+∠MEC=2∠ACB=90°,
∴MA⊥ME;
(2)成立.理由如下:
如解图,设AB与CF交于点N,在BF上截取BG=CM,连接AG,EG,MG,
∵∠BAC=∠F=90°,∠ANC=∠BNF,
∴∠ACM=∠FBA(三角形的内角和为180°),在△ABG和△ACM中,
∴ △ABG≌△ACM(SAS),
∴AG=AM,∠BAG=∠CAM,
∵∠BAC=90°,
∴∠GAM=90°,∵ BG=CM,DM=CM,
∴BG=DM,
在△EBG和△EDM中,
∴△EBG≌△EDM(SAS),
∴EG=EM,∠BEG=∠DEM,
∵ ∠BED = 90°,∴∠GEM=90°,
∴ ∠EGM = ∠EMG=∠AGM=∠AMG=45°, “海盗埋宝”模型)
∴∠AGE=∠AME=90°,
∴ 四边形AMEG 为矩形,
又∵EG=EM,∴ 四边形AMEG是正方形,
∴MA=ME,MA⊥ME.
模型展现
图示
条件 △ACD和△BEC是等腰直角三角形,A,B为直角顶点,且C点为公共点,连接DE,F 为DE的中点,连接FA,FB,AB
作法 延长AF至点 P,使得FP=AF,连接PE,PB,延长PE交AC于点 Q
结论 1. △DAF≌△EPF(SAS); 2. △ACB≌△PEB(SAS); 3.△ABP 是等腰直角三角形; 4.△FAB 是等腰直角三角形
结论分析
结论:1. △DAF≌△EPF(SAS);2. △ACB≌△PEB(SAS);
3. △ABP 是等腰直角三角形;4. △FAB 是等腰直角三角形
证明:如图,延长AF至点P,使得FP=AF,连接PE,PB,延长PE交AC 于点Q.
∵F为DE的中点,∴DF=EF.
在△DAF和△EPF中,
∴ △DAF≌△EPF(SAS)(结论1),
∴DA=EP,∠DAF=∠EPF,
∴DA∥PQ,
∴∠EQC=∠DAQ=90°.
在四边形 EQCB 中,∠EQC+∠EBC=90°+90°=180°,
∴∠QEB+∠QCB=180°.
又∵∠QEB+∠PEB=180°,
∴∠QCB=∠PEB.
∵△ACD 和△BEC 为等腰直角三角形,∴ AD=AC,BE=BC,∴AC=PE.
在△ACB 和△PEB中,
∴△ACB≌△PEB(SAS)(结论2),
∴AB=PB,∠ABC=∠PBE,
∴∠ABC+∠ABE=∠PBE+∠ABE,即∠CBE=∠ABP=90°,
∴ △ABP 是等腰直角三角形(结论3).
又∵F是AP 的中点,
∴BF⊥AP,BF=AF,
∴△FAB 是等腰直角三角形(结论4).
模型解题三步法
例 如图,在△ABC 中,分别以AC 和AB 为斜边,向△ABC 的内侧作等腰 Rt△AEC 和等腰Rt△ADB,F是BC的中点,连接FD,FE,DE,若FD=4,则线段DE的长为 .
中小学教育资源及组卷应用平台
题以类解
1. 如图,在△ABC中,∠ACB=90°,BC=AC,在等腰直角△BDE 中,∠BDE=90°,若 F 是AE的中点,则∠DFC 的度数为 ( )
A. 60° B. 90° C. 120° D. 150°
2. 如图,在等腰△ABC中,AB=AC,分别以AB,AC为斜边向△ABC的外侧作等腰 Rt△ADB和等腰 Rt△AEC,分别过点 D,E 作 DF⊥AB于点F,EG⊥AC 于点 G,若 M 是 BC 的中点,连接MD,ME,FM,GM,则下列结论不正确的是 ( )
A. BF=CG
B. MD=ME
C. △DFM 和△EGM 都是等腰三角形
D.四边形AFMG不是菱形
3.如图,在等腰Rt△ABC中,∠ABC=90°,延长BC 到点 E,以CE 为斜边,在 CE 下方作等腰Rt△CDE,连接 BD,AE,F 为 AE的中点,连接BF,DF.若AB=2,CD=3 ,则BF的长为 ,△BFD的面积为 .
4.如图,等腰 Rt△ABC 和等腰Rt△BDE有公共顶点 B,∠BAC=∠BDE=90°,连接CE,F是CE的中点,连接FA,FD.
(1)如图①,若D,A,B 三点共线,求证:AF∥BE;
(2)如图②,当∠ABD=45°,DF=4时,求AF的长.
5. 如图,△ABC 是等腰直角三角形,∠BAC=90°,四边形 BEDF是正方形,连接CD,M是CD的中点,连接AM,EM.
(1)如图①,当点 E 在线段BC 上时,求线段MA,ME的数量关系和位置关系;
(2)如图②,将图①中的△ABC 绕点 B 顺时针旋转,使点 C 落在 FD 的延长线上,其余条件都不变,则MA,ME的数量关系和位置关系仍然成立吗 请说明理由.
模型58 “海盗埋宝”模型
模型解题三步法
例 【解析】根据“海盗埋宝”模型作解图,∴ △DFE 是等腰直角三角形,∴FD=FE = 4,在 Rt △DFE
中,
题以类解
1. B 【解析】找模型:是否存在两个等腰直角三角形共底角顶点:△BDE 和△ABC,共顶点:点B,是否存在另一组底角顶点连线的中点:点F.抽离模型:如解图,用模型:根据“海盗埋宝”模型得,DF⊥CF,∴∠DFC=90°.
2. D 【解析】找模型:是否存在两个等腰直角三角形共底角顶点:△ADB 和△AEC,共顶点:点A,是否存在另一组底角顶点连线的中点:点M.抽离模型:如解图,用模型:根据“海盗埋宝”模型,得△DBM≌△ECM,∴ MD=ME,故B 选项正确,不符合题意;∵△ADB 和△AEC 是等腰直角三角形,∴∠ABD=∠DAB=∠ACE=∠EAC=45°,∠ADB=∠AEC=90°,在△ADB 和△AEC 中,△ADB≌△AEC(AAS),∴ BD=CE,AD=AE,∵DF⊥AB 于点 F,EG⊥AC 于点 G,∴DF= CG,故A 选项正确,不符合题意;∵F,M,G分别是AB,BC,AC的中点,∴MF,MG 是△ABC的中位线, 和△EGM都是等腰三角形,故C 选项正确,不符合题意;如解图,连接AM,∵AB=AC,M 是BC的中点,∴AM⊥BC,∴∠AMB=∠AMC= 90°,又∵ GM= AC=AG,∴AF=FM=GM=AG,∴四边形AFMG是菱形,故D 选项错误,符合题意.
【解析】∵AB=2,CD=3 ,∴BC=AB=2,CE= CD=6,∴BE=BC+CE=8,∴ ∵点F 是AE 的中点,∴ (直角三角形斜边中线等于斜边一半),由“海盗埋宝”模型知,△BFD 是等腰直角三角形,∴
4. (1)证明:如解图①,延长AF交DE于点M,∵∠CAD=∠BAC=∠BDE=90°,∴AC∥DE,∴∠ACF=∠MEF,
∵F为CE的中点,∴CF=EF,在△ACF和△MEF中,
∴△ACF≌△MEF(ASA),
∴AC=EM,AF=MF,
∵ △ABC 和△BDE是等腰直角三角形,
∴AB=AC,BD=DE,∠DEB=45°,
∵EM=AC=BA,
∴BD-AB=DE-EM,∴AD=DM,
又∵∠ADM=90°,∴∠DMA=45°=∠DEB,
∴AF∥BE;
(2)解:如解图②,延长CA 交 BD 于点 P,连接 PE,延长 ED与BA 的延长线交于点 G,连接CG,
∵△ABC是等腰直角三角形,
∴AB=AC,∠ABC=∠ACB=45°,∠BAC=90°,
∵∠ABD=45°,
∴∠APB=45°=∠ABD=∠ACB,
∴AB=AP,BC=BP,
∴AC=AP(等腰三角形“三线合一”),
∵F为CE的中点,
(中位线的性质).
同理可得
在△BCG和△BPE中,
∴△BCG≌△BPE(SAS)(“海盗埋宝”模型),
∴CG=PE,
∴AF=DF=4.
5. 解:(1)在△ACD中,
∵M是CD的中点,∠BAC=90°,
∴ ∠MAC=∠MCA.
∵四边形 BEDF 是正方形,
∴∠DEC=90°.
在△DEC中,∵M是CD的中点,
∴MA=ME,
∵∠MCA+∠MCE=∠ACB=45°,
∴ ∠AME=∠MAC+∠MCA+∠MCE+∠MEC=2∠ACB=90°,
∴MA⊥ME;
(2)成立.理由如下:
如解图,设AB与CF交于点N,在BF上截取BG=CM,连接AG,EG,MG,
∵∠BAC=∠F=90°,∠ANC=∠BNF,
∴∠ACM=∠FBA(三角形的内角和为180°),在△ABG和△ACM中,
∴ △ABG≌△ACM(SAS),
∴AG=AM,∠BAG=∠CAM,
∵∠BAC=90°,
∴∠GAM=90°,∵ BG=CM,DM=CM,
∴BG=DM,
在△EBG和△EDM中,
∴△EBG≌△EDM(SAS),
∴EG=EM,∠BEG=∠DEM,
∵ ∠BED = 90°,∴∠GEM=90°,
∴ ∠EGM = ∠EMG=∠AGM=∠AMG=45°, “海盗埋宝”模型)
∴∠AGE=∠AME=90°,
∴ 四边形AMEG 为矩形,
又∵EG=EM,∴ 四边形AMEG是正方形,
∴MA=ME,MA⊥ME.
同课章节目录
