模型 50 “飞鱼”模型(含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型 50 “飞鱼”模型(含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 327.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:39:52 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
模型 50 “飞鱼”模型
基础模型
飞鱼”模型与“斜8 字”燕尾型的区别:
“飞鱼”模型:已知的是两组对边相等,不产生相似三角形;
“斜8字”燕尾型:已知的是一组角相等,产生相似三角形.
结论:已知 则
证明:如图,过点D作DG∥BE交AC于点G,
拓展模型
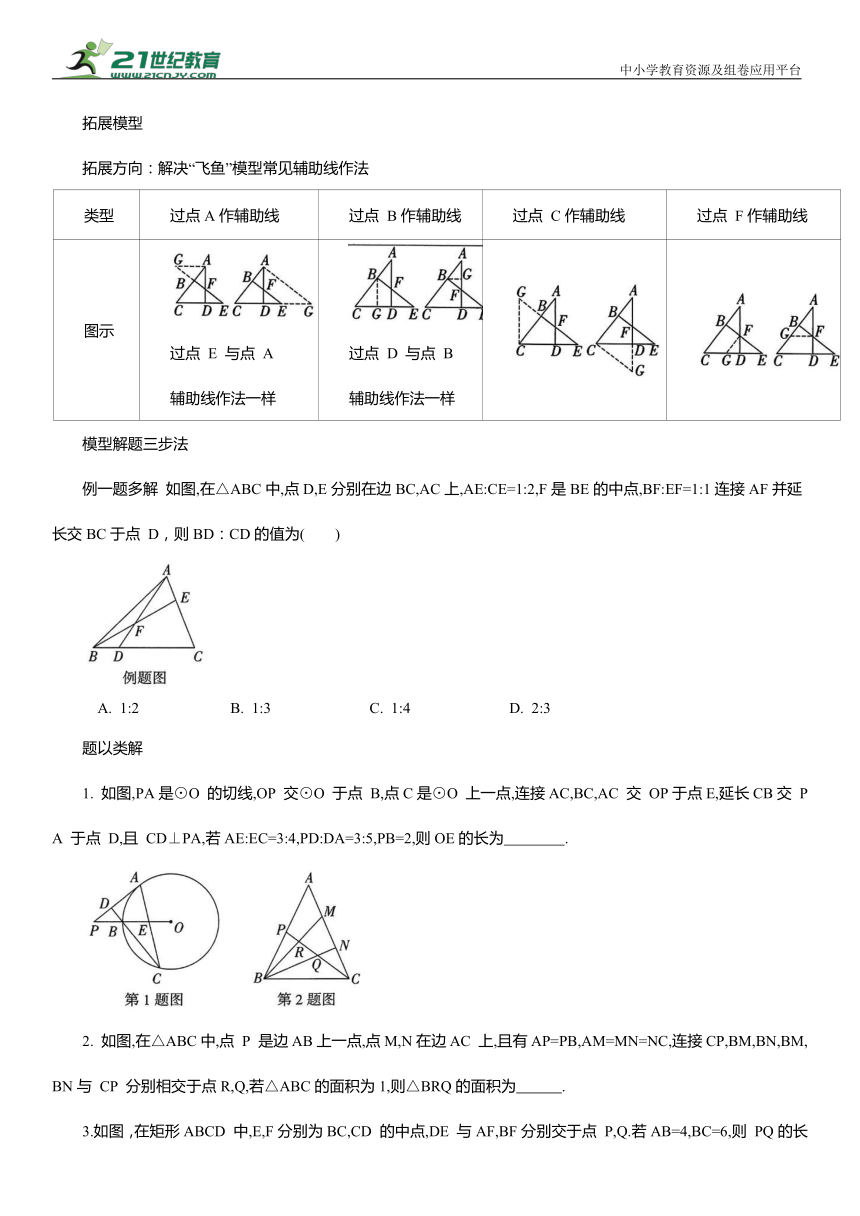
拓展方向:解决“飞鱼”模型常见辅助线作法
类型 过点A作辅助线 过点 B作辅助线 过点 C作辅助线 过点 F作辅助线
图示 过点 E 与点 A 辅助线作法一样 过点 D 与点 B 辅助线作法一样
模型解题三步法
例一题多解 如图,在△ABC中,点D,E分别在边BC,AC上,AE:CE=1:2,F是BE的中点,BF:EF=1:1连接AF并延长交BC于点 D,则BD:CD的值为( )
A. 1:2 B. 1:3 C. 1:4 D. 2:3
题以类解
1. 如图,PA是⊙O 的切线,OP 交⊙O 于点 B,点C是⊙O 上一点,连接AC,BC,AC 交 OP于点E,延长CB交 PA 于点 D,且 CD⊥PA,若AE:EC=3:4,PD:DA=3:5,PB=2,则OE的长为 .
2. 如图,在△ABC中,点 P 是边AB上一点,点M,N在边AC 上,且有AP=PB,AM=MN=NC,连接CP,BM,BN,BM,BN与 CP 分别相交于点R,Q,若△ABC的面积为1,则△BRQ的面积为 .
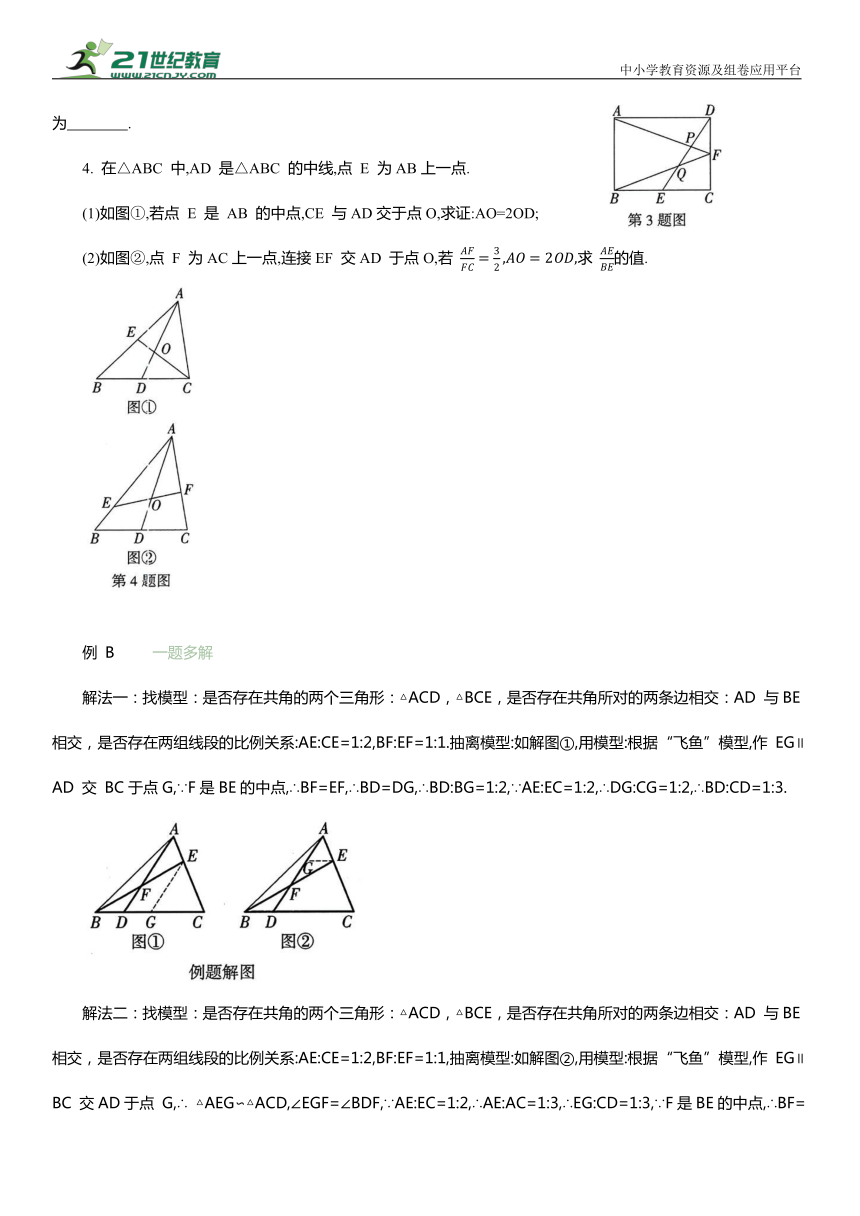
3.如图,在矩形ABCD 中,E,F分别为BC,CD 的中点,DE 与AF,BF分别交于点 P,Q.若AB=4,BC=6,则 PQ的长为 .
4. 在△ABC 中,AD 是△ABC 的中线,点 E 为AB上一点.
(1)如图①,若点 E 是 AB 的中点,CE 与AD交于点O,求证:AO=2OD;
(2)如图②,点 F 为AC上一点,连接EF 交AD 于点O,若 求 的值.
例 B 一题多解
解法一:找模型:是否存在共角的两个三角形:△ACD,△BCE,是否存在共角所对的两条边相交:AD 与BE 相交,是否存在两组线段的比例关系:AE:CE=1:2,BF:EF=1:1.抽离模型:如解图①,用模型:根据“飞鱼”模型,作 EG∥AD 交 BC于点G,∵F是BE的中点,∴BF=EF,∴BD=DG,∴BD:BG=1:2,∵AE:EC=1:2,∴DG:CG=1:2,∴BD:CD=1:3.
解法二:找模型:是否存在共角的两个三角形:△ACD,△BCE,是否存在共角所对的两条边相交:AD 与BE 相交,是否存在两组线段的比例关系:AE:CE=1:2,BF:EF=1:1,抽离模型:如解图②,用模型:根据“飞鱼”模型,作 EG∥BC 交AD于点 G,∴ △AEG∽△ACD,∠EGF=∠BDF,∵AE:EC=1:2,∴AE:AC=1:3,∴EG:CD=1:3,∵F是BE的中点,∴BF=EF,在△BDF 和△EGF中
∴BD=EG,∴BD:CD=1:3.
解法三:找模型:是否存在共角的两个三角形:△ACD,△BCE,是否存在共角所对的两条边相交:AD 与BE 相交,是否存在两组线段的比例关系:AE:CE=1:2,BF:EF=1:1,抽离模型:如解图③,用模型:根据“飞鱼”模型,取 EC 的中点 G,连接FG,∵F 是BE的中点,∴G是EC的中点,∵AE:EC=1:2,∴AE=EG=CG,∴AG:CG=2:1,∴AF:FD=2:1,∴S△AFB:S△BFD=2:1(两三角形同高),设S△BFD=S,则 又∵BF=EF,∴S△AFE:S△AFB=2S(等底同高的两三角形),∴ S△ABE=4S,∵AE:CE=1:2,∴S△BEC=2S△ABE=8S,∴ S四边形CEFD=7S,∴S△ADC=9S,S△ABD 即BD:CD=1:3.
题以类解
【解析】找模型:是否存在共角的两个三角形:△APE,△ACD;是否存在共角所对的两条边相交:PE与 CD 相交;是否存在两组线段的比例关系:AE:EC=3:4,PD:DA=3:5;抽离模型:如解图 ,用模型:根据“飞鱼”模型作解图,连接OA.过点 E 作 EF∥CD,交AP 于点 F.∵ PA 是⊙O 的切线,∴OA⊥PA(切线的性质),∵ CD⊥AP,∴ BD∥OA(同位角相等,两直线平行),∵ 平行线分线段成比例),
【解析】找模型1:是否存在共角的两个三角形:△ABM,△APC;是否存在共角所对的两条边相交:BM 与 CP 相交;是否存在两组线段的比例关系:AP:BP=1:1,AM:MC=1:2;抽离模型1:如解图,用模型1:根据“飞鱼”模型作解图,过P作PD∥AC,交BM于D;找模型2是否存在共角的两个三角形:△MCR,△MBN,是否存在共角所对的两条边相交:BN 与 CR 相交;是否存在两组线段的比例关系:MN:NC=1:1,BR:RM=3:2;抽离模型2:如解图 ,用模型2:根据“飞鱼”模型作解图,过 R 作 RE∥AC,交 BN于E.∵AP=PB,∴BD=DM,AM=2PD(中位线性质),∵ AM=MN=NC,∴ MC=4PD,∵ PD∥MC,∴△PDR∽△CMR(8字型相似),
【解析】根据“飞鱼”模型作解图,延长AF,BC 交于点 M,∵四边形ABCD 是矩形,AB=4,BC=6,∴∠DCB=90°,AD=BC=6,CD=AB=4.AB∥CD,AD∥BC(矩形的性质),∵ 点 E 是 BC的中点,∴BE=CE=3,在 Rt△DCE中,由勾股定理得 ∠FAD(两直线平行,内错角相等),∵ F 为 CD的中点,CD=4,∴CF = DF = 2,∵∠MFC = ∠AFD,∴ △MCF ≌△ADF(AAS),∴CM=AD=6(三角形全等的性质),即ME=6+3=9,∵AD∥BC,∴△MPE∽△APD(8字型相似),. DP=2,EP=3,延长DE 和AB 交于点N,同理可得AB=BN=4,∴AN=8,∵BC∥AD,∴DE=EN=5,∴DN=10.∵AB∥CD,∴△DQF∽△NQB(8字型相似). 解得DQ
4. (1)证明:如解图,过点 D 作 DG∥CE 交 AB 于点G.
∵AD 是BC边上的中线,∴BD=CD.
∴ BG=EG.
∵ E 是 AB 的中点,∴ BE:EA=1:1,
则AO:OD=AE:EG=2:1(“飞鱼”模型),∴AO=2OD;
(2)解:如解图②,延长 FE 和 CB 交于点 M,过点 D 作DN∥EF交AC 于点 N,则△AOF∽△ADN,△CMF∽△CDN,
∴AO:OD=AF:FN=2:1=6:3.
∵AF:FC=3:2=6:4,
∴FN:NC=MD:DC=3:1.
∵BD=CD,MD:CD=MD:BD=3:1(“飞鱼”模型).
如解图③,延长 FE 和 CB 交于点 M,过点 B作BP∥EF 交AD 于点 P,则△AOE∽△APB,△BDP∽△MDO,
∴MB:BD=OP:PD=2:1,
∵AO:OD=2:1=6:3,
∴AO:OP=6:2=AE:EB=3:1(“飞鱼”模型),
模型 50 “飞鱼”模型
基础模型
飞鱼”模型与“斜8 字”燕尾型的区别:
“飞鱼”模型:已知的是两组对边相等,不产生相似三角形;
“斜8字”燕尾型:已知的是一组角相等,产生相似三角形.
结论:已知 则
证明:如图,过点D作DG∥BE交AC于点G,
拓展模型
拓展方向:解决“飞鱼”模型常见辅助线作法
类型 过点A作辅助线 过点 B作辅助线 过点 C作辅助线 过点 F作辅助线
图示 过点 E 与点 A 辅助线作法一样 过点 D 与点 B 辅助线作法一样
模型解题三步法
例一题多解 如图,在△ABC中,点D,E分别在边BC,AC上,AE:CE=1:2,F是BE的中点,BF:EF=1:1连接AF并延长交BC于点 D,则BD:CD的值为( )
A. 1:2 B. 1:3 C. 1:4 D. 2:3
题以类解
1. 如图,PA是⊙O 的切线,OP 交⊙O 于点 B,点C是⊙O 上一点,连接AC,BC,AC 交 OP于点E,延长CB交 PA 于点 D,且 CD⊥PA,若AE:EC=3:4,PD:DA=3:5,PB=2,则OE的长为 .
2. 如图,在△ABC中,点 P 是边AB上一点,点M,N在边AC 上,且有AP=PB,AM=MN=NC,连接CP,BM,BN,BM,BN与 CP 分别相交于点R,Q,若△ABC的面积为1,则△BRQ的面积为 .
3.如图,在矩形ABCD 中,E,F分别为BC,CD 的中点,DE 与AF,BF分别交于点 P,Q.若AB=4,BC=6,则 PQ的长为 .
4. 在△ABC 中,AD 是△ABC 的中线,点 E 为AB上一点.
(1)如图①,若点 E 是 AB 的中点,CE 与AD交于点O,求证:AO=2OD;
(2)如图②,点 F 为AC上一点,连接EF 交AD 于点O,若 求 的值.
例 B 一题多解
解法一:找模型:是否存在共角的两个三角形:△ACD,△BCE,是否存在共角所对的两条边相交:AD 与BE 相交,是否存在两组线段的比例关系:AE:CE=1:2,BF:EF=1:1.抽离模型:如解图①,用模型:根据“飞鱼”模型,作 EG∥AD 交 BC于点G,∵F是BE的中点,∴BF=EF,∴BD=DG,∴BD:BG=1:2,∵AE:EC=1:2,∴DG:CG=1:2,∴BD:CD=1:3.
解法二:找模型:是否存在共角的两个三角形:△ACD,△BCE,是否存在共角所对的两条边相交:AD 与BE 相交,是否存在两组线段的比例关系:AE:CE=1:2,BF:EF=1:1,抽离模型:如解图②,用模型:根据“飞鱼”模型,作 EG∥BC 交AD于点 G,∴ △AEG∽△ACD,∠EGF=∠BDF,∵AE:EC=1:2,∴AE:AC=1:3,∴EG:CD=1:3,∵F是BE的中点,∴BF=EF,在△BDF 和△EGF中
∴BD=EG,∴BD:CD=1:3.
解法三:找模型:是否存在共角的两个三角形:△ACD,△BCE,是否存在共角所对的两条边相交:AD 与BE 相交,是否存在两组线段的比例关系:AE:CE=1:2,BF:EF=1:1,抽离模型:如解图③,用模型:根据“飞鱼”模型,取 EC 的中点 G,连接FG,∵F 是BE的中点,∴G是EC的中点,∵AE:EC=1:2,∴AE=EG=CG,∴AG:CG=2:1,∴AF:FD=2:1,∴S△AFB:S△BFD=2:1(两三角形同高),设S△BFD=S,则 又∵BF=EF,∴S△AFE:S△AFB=2S(等底同高的两三角形),∴ S△ABE=4S,∵AE:CE=1:2,∴S△BEC=2S△ABE=8S,∴ S四边形CEFD=7S,∴S△ADC=9S,S△ABD 即BD:CD=1:3.
题以类解
【解析】找模型:是否存在共角的两个三角形:△APE,△ACD;是否存在共角所对的两条边相交:PE与 CD 相交;是否存在两组线段的比例关系:AE:EC=3:4,PD:DA=3:5;抽离模型:如解图 ,用模型:根据“飞鱼”模型作解图,连接OA.过点 E 作 EF∥CD,交AP 于点 F.∵ PA 是⊙O 的切线,∴OA⊥PA(切线的性质),∵ CD⊥AP,∴ BD∥OA(同位角相等,两直线平行),∵ 平行线分线段成比例),
【解析】找模型1:是否存在共角的两个三角形:△ABM,△APC;是否存在共角所对的两条边相交:BM 与 CP 相交;是否存在两组线段的比例关系:AP:BP=1:1,AM:MC=1:2;抽离模型1:如解图,用模型1:根据“飞鱼”模型作解图,过P作PD∥AC,交BM于D;找模型2是否存在共角的两个三角形:△MCR,△MBN,是否存在共角所对的两条边相交:BN 与 CR 相交;是否存在两组线段的比例关系:MN:NC=1:1,BR:RM=3:2;抽离模型2:如解图 ,用模型2:根据“飞鱼”模型作解图,过 R 作 RE∥AC,交 BN于E.∵AP=PB,∴BD=DM,AM=2PD(中位线性质),∵ AM=MN=NC,∴ MC=4PD,∵ PD∥MC,∴△PDR∽△CMR(8字型相似),
【解析】根据“飞鱼”模型作解图,延长AF,BC 交于点 M,∵四边形ABCD 是矩形,AB=4,BC=6,∴∠DCB=90°,AD=BC=6,CD=AB=4.AB∥CD,AD∥BC(矩形的性质),∵ 点 E 是 BC的中点,∴BE=CE=3,在 Rt△DCE中,由勾股定理得 ∠FAD(两直线平行,内错角相等),∵ F 为 CD的中点,CD=4,∴CF = DF = 2,∵∠MFC = ∠AFD,∴ △MCF ≌△ADF(AAS),∴CM=AD=6(三角形全等的性质),即ME=6+3=9,∵AD∥BC,∴△MPE∽△APD(8字型相似),. DP=2,EP=3,延长DE 和AB 交于点N,同理可得AB=BN=4,∴AN=8,∵BC∥AD,∴DE=EN=5,∴DN=10.∵AB∥CD,∴△DQF∽△NQB(8字型相似). 解得DQ
4. (1)证明:如解图,过点 D 作 DG∥CE 交 AB 于点G.
∵AD 是BC边上的中线,∴BD=CD.
∴ BG=EG.
∵ E 是 AB 的中点,∴ BE:EA=1:1,
则AO:OD=AE:EG=2:1(“飞鱼”模型),∴AO=2OD;
(2)解:如解图②,延长 FE 和 CB 交于点 M,过点 D 作DN∥EF交AC 于点 N,则△AOF∽△ADN,△CMF∽△CDN,
∴AO:OD=AF:FN=2:1=6:3.
∵AF:FC=3:2=6:4,
∴FN:NC=MD:DC=3:1.
∵BD=CD,MD:CD=MD:BD=3:1(“飞鱼”模型).
如解图③,延长 FE 和 CB 交于点 M,过点 B作BP∥EF 交AD 于点 P,则△AOE∽△APB,△BDP∽△MDO,
∴MB:BD=OP:PD=2:1,
∵AO:OD=2:1=6:3,
∴AO:OP=6:2=AE:EB=3:1(“飞鱼”模型),
同课章节目录
