模型33 含60°角的菱形 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型33 含60°角的菱形 (含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 287.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:38:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
模型33 含60°角的菱形
模型展现
图示
条件 四边形ABCD为菱形,对角线AC与BD交于点O,∠ABC=60°
结论 1. ∠ABD=∠CBD=30°; 2. △ABC和△ACD均为等边三角形; 3. AB:AC:BD=1:1: 4. S要形ACD= AC ·BD= BC
结论:1.
和 均为等边三角形;
证明:∵四边形ABCD为菱形,
(结论1),
和 均为等边三角形(有一个内角为 的等腰三角形是等边三角形)(结论2).
在 中,
∵AB=AC=BC.∴AB:AC:BD=1:1: (结论3),
如图,过点A作 于点E,
在 中,
(菱形面积公式),
(结论4).
模型解题三步法
例 如图,在菱形ABCD中,对角线AC,BD 相交于点O.若 则菱形ABCD的 周长为 ( )
题以类解
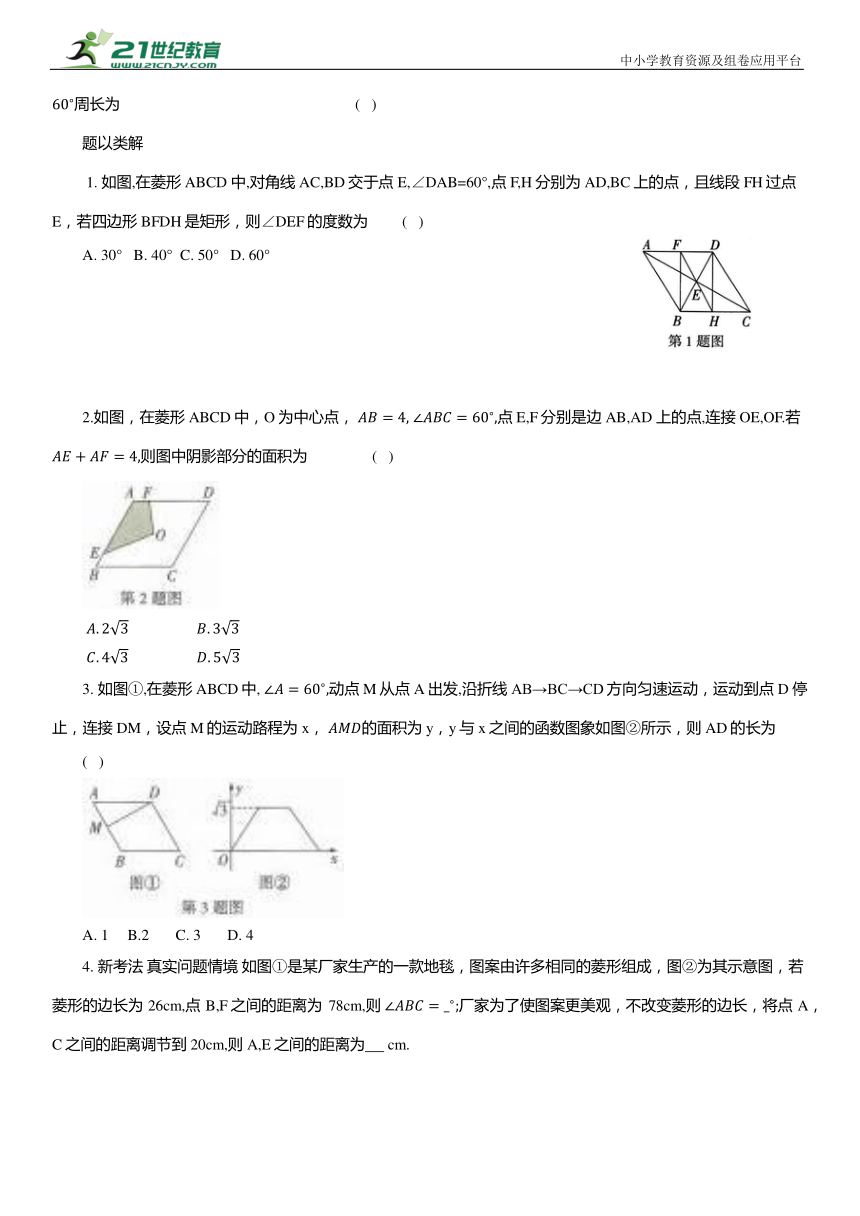
1. 如图,在菱形ABCD 中,对角线AC,BD交于点E,∠DAB=60°,点 F,H分别为AD,BC上的点,且线段 FH过点 E,若四边形BFDH是矩形,则∠DEF的度数为 ( )
A. 30° B. 40° C. 50° D. 60°
2.如图,在菱形ABCD中,O为中心点, 点E,F分别是边AB,AD 上的点,连接OE,OF.若 则图中阴影部分的面积为 ( )
3. 如图①,在菱形ABCD中, 动点M从点A 出发,沿折线AB→BC→CD方向匀速运动,运动到点 D 停止,连接DM,设点M的运动路程为x, 的面积为y,y与x之间的函数图象如图②所示,则AD的长为
( )
A. 1 B.2 C. 3 D. 4
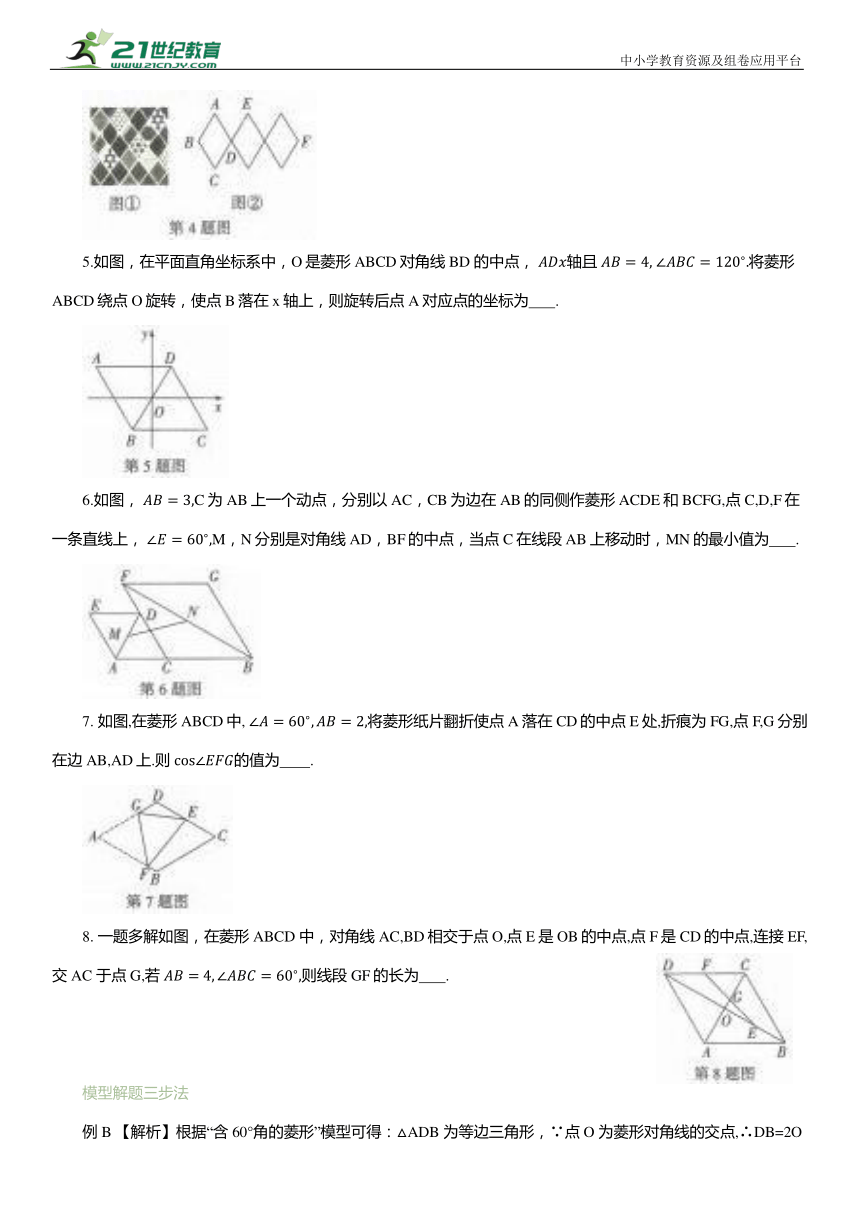
4. 新考法 真实问题情境 如图①是某厂家生产的一款地毯,图案由许多相同的菱形组成,图②为其示意图,若菱形的边长为26cm,点B,F之间的距离为 78cm,则 厂家为了使图案更美观,不改变菱形的边长,将点A,C之间的距离调节到20cm,则A,E之间的距离为 cm.
5.如图,在平面直角坐标系中,O是菱形ABCD对角线 BD 的中点, 轴且 将菱形ABCD绕点O旋转,使点B落在x轴上,则旋转后点A对应点的坐标为 .
6.如图, C为AB上一个动点,分别以AC,CB为边在AB的同侧作菱形ACDE和BCFG,点C,D,F在一条直线上, M,N分别是对角线AD,BF的中点,当点C在线段AB上移动时,MN的最小值为 .
7. 如图,在菱形ABCD中, 将菱形纸片翻折使点A落在CD的中点E处,折痕为FG,点 F,G分别在边AB,AD上.则 的值为 .
8. 一题多解如图,在菱形ABCD 中,对角线AC,BD相交于点O,点E是OB的中点,点F是CD的中点,连接EF,交AC 于点G,若 则线段GF的长为 .
模型解题三步法
例 B 【解析】根据“含60°角的菱形”模型可得:△ADB 为等边三角形,∵点 O 为菱形对角线的交点,∴DB=2OD=6,∴AD=DB=6,∴菱形ABCD的周长为24.
题以类解
1. D 【解析】找模型 菱形中是否存在60°的角:∠DAB=60°,抽离模型 如解图,用模型:根据“含60°角的菱形”模型可得:△ADB 为等边三角形,则∠ADB=60°,∵四边形 BFDH是矩形,∴BD=FH,∴EF=DE,∴△EFD 为等边三角形,∴∠DEF=60°.
2. A 【解析】找模型:菱形中是否存在60°的角:∠ABC=60°,抽离模型:如解图,用模型:连接OA,OB,∵AE+AF=4,AB=4,∴AF=BE,∴S△BOE=S△AOF(菱形的中心点到各边的距离相等), 根据“含60°角的菱形”模型可得:∠ABO=30°,AO⊥BO,∴OA=AB·sin30°=2,OB=AB·cos30°=2
3. B 【解析】如解图,当点 M运动到 BC 段时,△ABD 的面积为 ,过点 M 作 ME⊥AD 于点 E,∵ 四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∵BE⊥AD,∴BE=AB·sin60° 解得AD=2(负值已舍去).
4. 120;48 【解析】当B,F之间的距离为78cm时,B,D之间的距离为26 cm,如解图①,连接BD,则△ABD为等边三角形,∴∠BAD=60°,∴∠ABC=120°;如解图②,连接AC,AE,BD,AC与BD交于点O,当AC=20cm时,AO=10 cm,∵AB=26 cm,∴ BO=√AB -AO =24 cm,∴AE=BD=2BO=48 cm.
5. (0,2 )或( 【解析】如解图①,根据菱形的对称性可得:当点 B 旋转到x轴负半轴时,A,C,D 均在坐标轴上,∵ ∠ABC=120°,∴ ∠BAD=60°,∴ △ABD 为等边三角形,∴ ∠OAB=30°(“含60°角的菱形”模型),∵AB=4,∴OB=2,∴AO=AB·cos30°=2 ,∴点A的坐标为(0,2 ),同理:如解图②,当点 B 旋转到x 轴正半轴时,点A 的坐标为 ,综上所述,旋转后点 A 对应点的坐标为(0,2 )或(
6. 2 【解析】如解图,连接 CM,CN.∵∠E=60°,AE=ED,∴△ADE 为等边三角形,同理,△ADC 为等边三角形(“含60°角的菱形”模型). ∴∠DCA=60°,∠BCF=120°,∵ M,N分别是对角线AD,BF 的中点,∴ ∠DCM= ,设 AC =2a,则 ∴ 当a=1时,MN有最小值,最小值为2
【解析】如解图,连接BE,BD,连接AE 交 FG 于点 H,由折叠的性质可得∠GAF=∠GEF=60°,∵ BC=CD,∴ △BDC为等边三角形(“含60°角的菱形”模型),∵ 点 E 为CD的中点,∴CE=DE=1,∠BEC=90°,在 Rt△BCE中, .∠EBF = 90°,∴ 在 Rt △AEB 中, AE = 设EF=AF=x,则BF=2-x,在Rt△BEF中,( 解得 在 Rt△AHF中
解法一:
如解图①,取 OD 的中点 H,连接 FH,∵∠ABC=60°,AB=BC,∴ △ABC 为等边三角形(“含60°角的菱形”模型),∴AB=BC=AC 又∵点 E 是 OB 的中点,. ∵点 F 是 CD 的中点,点 H 是OD 的中点,∴ HF 是△OCD的中位线, ,∴点O 是EH的中点,∴OG是△EFH的中位线,
解法二:
如解图②,过点 D 作 DI∥EF,交AC 于点I,∵∠ABC=60°,AB=BC,∴ △ABC 为等边三角形(“含60°角的菱形”模型),∴AB=BC= ,∵ 点 E 是 OB 的中点,点 F 是 CD 的中点, 设OG=k,则OI=2k, 在 Rt △IDO 中, GF 是△DCI的中位线.
模型33 含60°角的菱形
模型展现
图示
条件 四边形ABCD为菱形,对角线AC与BD交于点O,∠ABC=60°
结论 1. ∠ABD=∠CBD=30°; 2. △ABC和△ACD均为等边三角形; 3. AB:AC:BD=1:1: 4. S要形ACD= AC ·BD= BC
结论:1.
和 均为等边三角形;
证明:∵四边形ABCD为菱形,
(结论1),
和 均为等边三角形(有一个内角为 的等腰三角形是等边三角形)(结论2).
在 中,
∵AB=AC=BC.∴AB:AC:BD=1:1: (结论3),
如图,过点A作 于点E,
在 中,
(菱形面积公式),
(结论4).
模型解题三步法
例 如图,在菱形ABCD中,对角线AC,BD 相交于点O.若 则菱形ABCD的 周长为 ( )
题以类解
1. 如图,在菱形ABCD 中,对角线AC,BD交于点E,∠DAB=60°,点 F,H分别为AD,BC上的点,且线段 FH过点 E,若四边形BFDH是矩形,则∠DEF的度数为 ( )
A. 30° B. 40° C. 50° D. 60°
2.如图,在菱形ABCD中,O为中心点, 点E,F分别是边AB,AD 上的点,连接OE,OF.若 则图中阴影部分的面积为 ( )
3. 如图①,在菱形ABCD中, 动点M从点A 出发,沿折线AB→BC→CD方向匀速运动,运动到点 D 停止,连接DM,设点M的运动路程为x, 的面积为y,y与x之间的函数图象如图②所示,则AD的长为
( )
A. 1 B.2 C. 3 D. 4
4. 新考法 真实问题情境 如图①是某厂家生产的一款地毯,图案由许多相同的菱形组成,图②为其示意图,若菱形的边长为26cm,点B,F之间的距离为 78cm,则 厂家为了使图案更美观,不改变菱形的边长,将点A,C之间的距离调节到20cm,则A,E之间的距离为 cm.
5.如图,在平面直角坐标系中,O是菱形ABCD对角线 BD 的中点, 轴且 将菱形ABCD绕点O旋转,使点B落在x轴上,则旋转后点A对应点的坐标为 .
6.如图, C为AB上一个动点,分别以AC,CB为边在AB的同侧作菱形ACDE和BCFG,点C,D,F在一条直线上, M,N分别是对角线AD,BF的中点,当点C在线段AB上移动时,MN的最小值为 .
7. 如图,在菱形ABCD中, 将菱形纸片翻折使点A落在CD的中点E处,折痕为FG,点 F,G分别在边AB,AD上.则 的值为 .
8. 一题多解如图,在菱形ABCD 中,对角线AC,BD相交于点O,点E是OB的中点,点F是CD的中点,连接EF,交AC 于点G,若 则线段GF的长为 .
模型解题三步法
例 B 【解析】根据“含60°角的菱形”模型可得:△ADB 为等边三角形,∵点 O 为菱形对角线的交点,∴DB=2OD=6,∴AD=DB=6,∴菱形ABCD的周长为24.
题以类解
1. D 【解析】找模型 菱形中是否存在60°的角:∠DAB=60°,抽离模型 如解图,用模型:根据“含60°角的菱形”模型可得:△ADB 为等边三角形,则∠ADB=60°,∵四边形 BFDH是矩形,∴BD=FH,∴EF=DE,∴△EFD 为等边三角形,∴∠DEF=60°.
2. A 【解析】找模型:菱形中是否存在60°的角:∠ABC=60°,抽离模型:如解图,用模型:连接OA,OB,∵AE+AF=4,AB=4,∴AF=BE,∴S△BOE=S△AOF(菱形的中心点到各边的距离相等), 根据“含60°角的菱形”模型可得:∠ABO=30°,AO⊥BO,∴OA=AB·sin30°=2,OB=AB·cos30°=2
3. B 【解析】如解图,当点 M运动到 BC 段时,△ABD 的面积为 ,过点 M 作 ME⊥AD 于点 E,∵ 四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∵BE⊥AD,∴BE=AB·sin60° 解得AD=2(负值已舍去).
4. 120;48 【解析】当B,F之间的距离为78cm时,B,D之间的距离为26 cm,如解图①,连接BD,则△ABD为等边三角形,∴∠BAD=60°,∴∠ABC=120°;如解图②,连接AC,AE,BD,AC与BD交于点O,当AC=20cm时,AO=10 cm,∵AB=26 cm,∴ BO=√AB -AO =24 cm,∴AE=BD=2BO=48 cm.
5. (0,2 )或( 【解析】如解图①,根据菱形的对称性可得:当点 B 旋转到x轴负半轴时,A,C,D 均在坐标轴上,∵ ∠ABC=120°,∴ ∠BAD=60°,∴ △ABD 为等边三角形,∴ ∠OAB=30°(“含60°角的菱形”模型),∵AB=4,∴OB=2,∴AO=AB·cos30°=2 ,∴点A的坐标为(0,2 ),同理:如解图②,当点 B 旋转到x 轴正半轴时,点A 的坐标为 ,综上所述,旋转后点 A 对应点的坐标为(0,2 )或(
6. 2 【解析】如解图,连接 CM,CN.∵∠E=60°,AE=ED,∴△ADE 为等边三角形,同理,△ADC 为等边三角形(“含60°角的菱形”模型). ∴∠DCA=60°,∠BCF=120°,∵ M,N分别是对角线AD,BF 的中点,∴ ∠DCM= ,设 AC =2a,则 ∴ 当a=1时,MN有最小值,最小值为2
【解析】如解图,连接BE,BD,连接AE 交 FG 于点 H,由折叠的性质可得∠GAF=∠GEF=60°,∵ BC=CD,∴ △BDC为等边三角形(“含60°角的菱形”模型),∵ 点 E 为CD的中点,∴CE=DE=1,∠BEC=90°,在 Rt△BCE中, .∠EBF = 90°,∴ 在 Rt △AEB 中, AE = 设EF=AF=x,则BF=2-x,在Rt△BEF中,( 解得 在 Rt△AHF中
解法一:
如解图①,取 OD 的中点 H,连接 FH,∵∠ABC=60°,AB=BC,∴ △ABC 为等边三角形(“含60°角的菱形”模型),∴AB=BC=AC 又∵点 E 是 OB 的中点,. ∵点 F 是 CD 的中点,点 H 是OD 的中点,∴ HF 是△OCD的中位线, ,∴点O 是EH的中点,∴OG是△EFH的中位线,
解法二:
如解图②,过点 D 作 DI∥EF,交AC 于点I,∵∠ABC=60°,AB=BC,∴ △ABC 为等边三角形(“含60°角的菱形”模型),∴AB=BC= ,∵ 点 E 是 OB 的中点,点 F 是 CD 的中点, 设OG=k,则OI=2k, 在 Rt △IDO 中, GF 是△DCI的中位线.
同课章节目录
