模型30 “垂美四边形”模型 (含答案)2025年中考数学几何模型专题复习
文档属性
| 名称 | 模型30 “垂美四边形”模型 (含答案)2025年中考数学几何模型专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 234.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:37:45 | ||
图片预览

文档简介
模型30 “垂美四边形”模型
模型展现
定义 对角线互相垂直的四边形叫做垂美四边形
图示
条件 在四边形ABCD 中,AC⊥BD.
结论 1. AB +CD =AD +BC ; 2. S = AC·BD
结论分析
结论1:
证明:∵AC⊥BD,根据勾股定理得:
结论
自主证明:
模型解题三步法
例 如图,在四边形ABCD中,对角线AC,BD交于点O, 若 则
中小学教育资源及组卷应用平台
题以类解
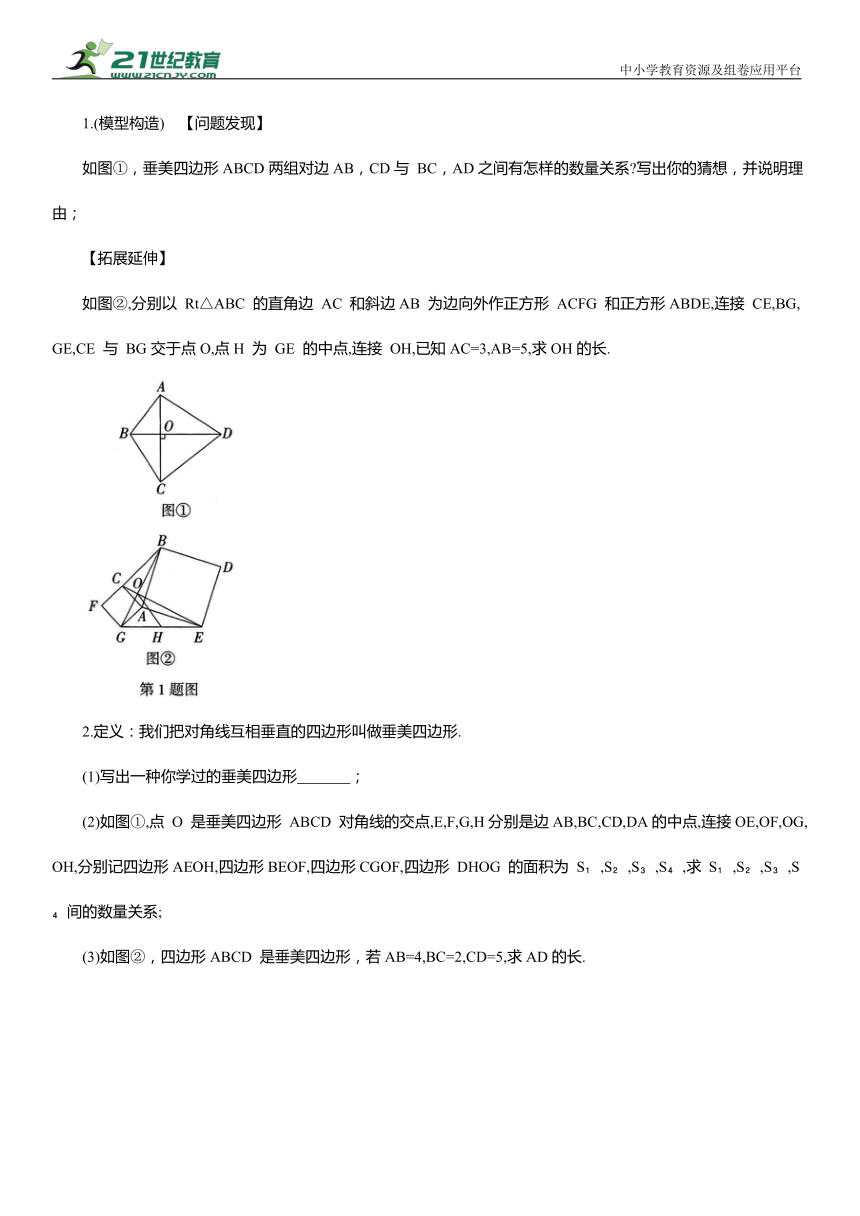
1.(模型构造) 【问题发现】
如图①,垂美四边形ABCD两组对边AB,CD与 BC,AD之间有怎样的数量关系 写出你的猜想,并说明理由;
【拓展延伸】
如图②,分别以 Rt△ABC 的直角边 AC 和斜边AB 为边向外作正方形 ACFG 和正方形ABDE,连接 CE,BG,GE,CE 与 BG交于点O,点H 为 GE 的中点,连接 OH,已知AC=3,AB=5,求OH的长.
2.定义:我们把对角线互相垂直的四边形叫做垂美四边形.
(1)写出一种你学过的垂美四边形 ;
(2)如图①,点 O 是垂美四边形 ABCD 对角线的交点,E,F,G,H分别是边AB,BC,CD,DA的中点,连接OE,OF,OG,OH,分别记四边形AEOH,四边形BEOF,四边形CGOF,四边形 DHOG 的面积为 S ,S ,S ,S ,求 S ,S ,S ,S 间的数量关系;
(3)如图②,四边形ABCD 是垂美四边形,若AB=4,BC=2,CD=5,求AD的长.
自主证明:
模型解题三步法
例 13 【解析】找模型 图形背景是否为四边形:四边形ABCD;四边形中是否存在垂直的对角线:AC⊥BD;抽离模型:如解图,用模型
根据“垂美四边形”模型得 ∵ AD
题以类解
1.解:【问题发现】
猜想:
理由:∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得:
【拓展延伸】
如解图,连接 CG,BE,设AB,CE交于点M,
∵ ∠CAG = ∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE(等角代换),在△GAB 和△CAE中,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC.
又∵∠AEC+∠AME=90°,∠OMB=∠AME,
∴∠ABG+∠AME=∠ABG+∠OMB=90°,
∴∠BOM=90°,即CE⊥BG,
∴ 四边形 CGEB 是垂美四边形(垂美四边形的定义),
(“垂美四边形”模型),
∵AC=3,AB=5,
(负值已舍去),
(直角三角形斜边中线性质).
2. 解:(1)正方形(或菱形);
(2)如解图①,连接AC,BD,由垂美四边形的定义可知AC⊥BD,
则∠AOB=∠BOC=∠COD=∠DOA=90°,
又∵E,F,G,H分别是边AB,BC,CD,DA的中点,
(3)如解图②,连接AC,BD交于点 O,由垂美四边形的定义可知AC⊥BD,
在 Rt△AOD中,
在 Rt△AOB 中,
在 Rt△BOC 中,
在 Rt△DOC中,
∵AB=4,BC=2,CD=5,
即 (负值已舍去).
模型展现
定义 对角线互相垂直的四边形叫做垂美四边形
图示
条件 在四边形ABCD 中,AC⊥BD.
结论 1. AB +CD =AD +BC ; 2. S = AC·BD
结论分析
结论1:
证明:∵AC⊥BD,根据勾股定理得:
结论
自主证明:
模型解题三步法
例 如图,在四边形ABCD中,对角线AC,BD交于点O, 若 则
中小学教育资源及组卷应用平台
题以类解
1.(模型构造) 【问题发现】
如图①,垂美四边形ABCD两组对边AB,CD与 BC,AD之间有怎样的数量关系 写出你的猜想,并说明理由;
【拓展延伸】
如图②,分别以 Rt△ABC 的直角边 AC 和斜边AB 为边向外作正方形 ACFG 和正方形ABDE,连接 CE,BG,GE,CE 与 BG交于点O,点H 为 GE 的中点,连接 OH,已知AC=3,AB=5,求OH的长.
2.定义:我们把对角线互相垂直的四边形叫做垂美四边形.
(1)写出一种你学过的垂美四边形 ;
(2)如图①,点 O 是垂美四边形 ABCD 对角线的交点,E,F,G,H分别是边AB,BC,CD,DA的中点,连接OE,OF,OG,OH,分别记四边形AEOH,四边形BEOF,四边形CGOF,四边形 DHOG 的面积为 S ,S ,S ,S ,求 S ,S ,S ,S 间的数量关系;
(3)如图②,四边形ABCD 是垂美四边形,若AB=4,BC=2,CD=5,求AD的长.
自主证明:
模型解题三步法
例 13 【解析】找模型 图形背景是否为四边形:四边形ABCD;四边形中是否存在垂直的对角线:AC⊥BD;抽离模型:如解图,用模型
根据“垂美四边形”模型得 ∵ AD
题以类解
1.解:【问题发现】
猜想:
理由:∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得:
【拓展延伸】
如解图,连接 CG,BE,设AB,CE交于点M,
∵ ∠CAG = ∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE(等角代换),在△GAB 和△CAE中,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC.
又∵∠AEC+∠AME=90°,∠OMB=∠AME,
∴∠ABG+∠AME=∠ABG+∠OMB=90°,
∴∠BOM=90°,即CE⊥BG,
∴ 四边形 CGEB 是垂美四边形(垂美四边形的定义),
(“垂美四边形”模型),
∵AC=3,AB=5,
(负值已舍去),
(直角三角形斜边中线性质).
2. 解:(1)正方形(或菱形);
(2)如解图①,连接AC,BD,由垂美四边形的定义可知AC⊥BD,
则∠AOB=∠BOC=∠COD=∠DOA=90°,
又∵E,F,G,H分别是边AB,BC,CD,DA的中点,
(3)如解图②,连接AC,BD交于点 O,由垂美四边形的定义可知AC⊥BD,
在 Rt△AOD中,
在 Rt△AOB 中,
在 Rt△BOC 中,
在 Rt△DOC中,
∵AB=4,BC=2,CD=5,
即 (负值已舍去).
同课章节目录
