2024-2025学年北师大版七年级数学下册1.3乘法公式课时2 平方差公式的应用 课件(共27张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册1.3乘法公式课时2 平方差公式的应用 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 990.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:23:02 | ||
图片预览



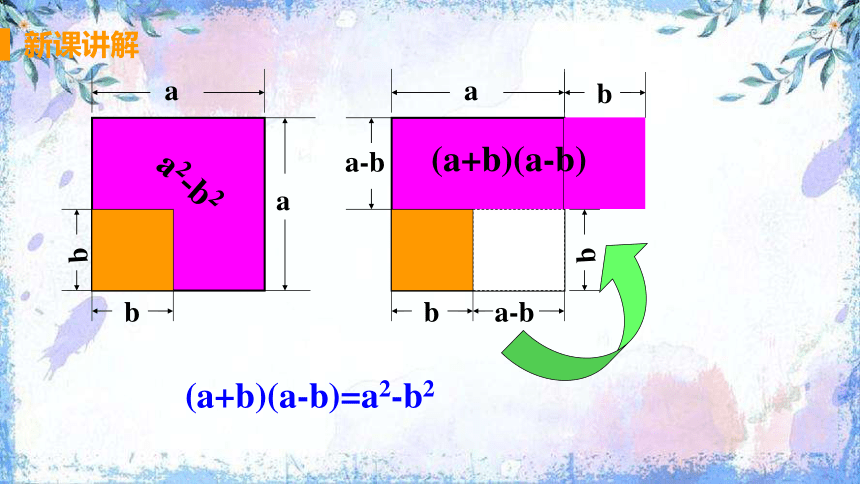



文档简介
(共27张PPT)
北师大版七年级数学下册课件
第一章 整式的乘除
1.3 乘法公式
课时2 平方差公式的应用
1.掌握平方差公式的结构特征,能运用公式进行简便运算;
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.
学习目标
新课讲解
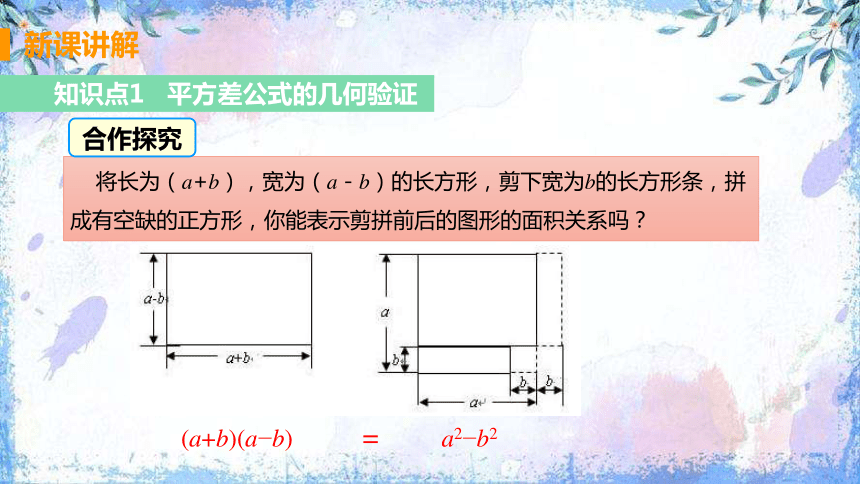
知识点1 平方差公式的几何验证
将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条,拼成有空缺的正方形,你能表示剪拼前后的图形的面积关系吗?
(a+b)(a b) = a2 b2
合作探究
新课讲解
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
新课讲解
知识点2 平方差公式的运用
自主探究
想一想:
(1)计算下列各式,并观察他们的共同特点:
6×8=48 14×16=224 69×71=4899
7×7=49 15×15=225 70×70=4900
新课讲解
(2)从以上的过程中,你发现了什么规律?请用字母表示这一规律,你能说明它的正确性吗?
(a+b)(a b)=a2 b2
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
当堂小练
解:(1)原式=(50+1)(50-1)
=502-12
=2500-1=2499;
(3)原式=(9x2-16)-(6x2+5x-6)
=3x2-5x-10.
(1)51×49;
(3)(3x+4)(3x-4)-(2x+3)(3x-2).
(2)13.2×12.8;
.利用平方差公式计算:
(2)原式=(13+0.2)×(13-0.2)
=132-0.22
=169-0.04=168.96.
拓展与延伸
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
(北师7下P19、人教8上P107)如图1,边长为a的大正方形中有一个边长为b的小正方形.
(1)图1中阴影部分的面积为 (作差法);
知识点 1
利用图形验证平方差公式
图1
a2-b2
(2)小颖将阴影部分拼成一个长方形(如图2 ),
这个长方形的长为 ,宽为 ,
它的面积为 ;
(3)通过计算阴影部分的面积,验证了一个等式,
这个等式是 .
图2
a+b
a-b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
1.(北师7下P19、人教8上P107)如图,将边长为x(x>1)的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成一个大的长方形,这两个图能解释一个等式是( )
A.x2-x=x(x-1)
B.x2-1=(x+1)(x-1)
C.x2-2x+1=(x-1)2
D.x2+2x+1=(x+1)2
B
(1)利用平方差公式,可对一些特殊数进行简化计算.解答此类题目的关键是恰当变形,将其变化为两数和与两数差的积的形式.
(2)例如,计算29×31时,可先把29写成30-1,31写成30+1,即29×31=(30-1)× (30+1),然后运用平方差公式计算即可.
知识点 2
利用平方差公式进行简便计算
2.巧用公式计算:18×20-192.
解:原式=(19-1)(19+1)-192
=192-1-192= -1.
有的计算虽然不能从整体上用平方差公式,但可将其中一部分套入公式,适当拆项使整个运算更简捷些.
平方差公式的应用
知识点 3
3.计算:x(x+2)+(1+x)(1-x).
解:原式=x2+2x+1-x2=2x+1.
4.【例1】如图,利用图1和图2的阴影面积相等,写出一个正确的等式: .
(a+2)(a-2)=a2-4
5.【例2】计算:
(1)203×197;
(2)(x+2y)(x-2y)-y(3-4y).
解:原式=(200+3)(200-3)=2002-32
=40 000-9=39 991.
解:原式=x2-4y2-(3y-4y2)
=x2-4y2-3y+4y2=x2-3y.
6.【例3】先化简,再求值:
(2+a)(2-a)-,其中a=2.
解:原式=4-a2-a2+1=5- a2.
当a=2时,
原式=5- ×4=0.
7.(创新题)在边长为a的正方形中挖掉一个边长为b的小正方形
(a>b),把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是
( )
A.a2-b2=(a+b)(a-b)
B.(a+b)2 =a2+2ab+b2
C.(a-b)2=a2-2ab+b2
D.a2-ab=a(a-b)
A
8.用平方差公式计算:
(1)2 023×2 025-2 0242;
(2)(a+3b)(a-3b)(a2+9b2).
解:原式=(2 024-1)×(2 024+1)-2 0242
=2 0242-1-2 0242=1.
解:原式=(a2-9b2)(a2+9b2)=a4-81b4.
9.已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
解:原式=9x2-4+x2-2x=10x2-2x-4,
因为5x2-x-1=0,所以5x2-x=1.
所以原式=2(5x2-x)-4= -2.
★10. 0.40(代数推理)观察下列各式:(2+3)2-22=7×3;(4+3)2-42=11×3;(6+3)2-62=15×3,….不难发现规律:比任意一个偶数大3的数与此偶数的平方差能被3整除.
(1)(8+3)2-82的结果是3的 倍;
(2)设偶数为2n,试说明比2n大5的数与2n的平方差能被5整除;
解:(2)根据题意可知,设偶数为2n,则比2n大5的数为2n+5,
因为(2n+5)2-(2n)2=(2n+5-2n)(2n+5+2n)=5(4n+5),4n+5为整数,所以5(4n+5)能被5整除,
所以比2n大5的数与2n的平方差能被5整除.
19
(3)拓展:比任意一个正整数大5的数与此整数的平方差除以10的余数是 .
5
布置作业
请完成课后对应习题
感谢大家观看
北师大版七年级数学下册课件
第一章 整式的乘除
1.3 乘法公式
课时2 平方差公式的应用
1.掌握平方差公式的结构特征,能运用公式进行简便运算;
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.
学习目标
新课讲解
知识点1 平方差公式的几何验证
将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条,拼成有空缺的正方形,你能表示剪拼前后的图形的面积关系吗?
(a+b)(a b) = a2 b2
合作探究
新课讲解
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
新课讲解
知识点2 平方差公式的运用
自主探究
想一想:
(1)计算下列各式,并观察他们的共同特点:
6×8=48 14×16=224 69×71=4899
7×7=49 15×15=225 70×70=4900
新课讲解
(2)从以上的过程中,你发现了什么规律?请用字母表示这一规律,你能说明它的正确性吗?
(a+b)(a b)=a2 b2
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
当堂小练
解:(1)原式=(50+1)(50-1)
=502-12
=2500-1=2499;
(3)原式=(9x2-16)-(6x2+5x-6)
=3x2-5x-10.
(1)51×49;
(3)(3x+4)(3x-4)-(2x+3)(3x-2).
(2)13.2×12.8;
.利用平方差公式计算:
(2)原式=(13+0.2)×(13-0.2)
=132-0.22
=169-0.04=168.96.
拓展与延伸
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
(北师7下P19、人教8上P107)如图1,边长为a的大正方形中有一个边长为b的小正方形.
(1)图1中阴影部分的面积为 (作差法);
知识点 1
利用图形验证平方差公式
图1
a2-b2
(2)小颖将阴影部分拼成一个长方形(如图2 ),
这个长方形的长为 ,宽为 ,
它的面积为 ;
(3)通过计算阴影部分的面积,验证了一个等式,
这个等式是 .
图2
a+b
a-b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
1.(北师7下P19、人教8上P107)如图,将边长为x(x>1)的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成一个大的长方形,这两个图能解释一个等式是( )
A.x2-x=x(x-1)
B.x2-1=(x+1)(x-1)
C.x2-2x+1=(x-1)2
D.x2+2x+1=(x+1)2
B
(1)利用平方差公式,可对一些特殊数进行简化计算.解答此类题目的关键是恰当变形,将其变化为两数和与两数差的积的形式.
(2)例如,计算29×31时,可先把29写成30-1,31写成30+1,即29×31=(30-1)× (30+1),然后运用平方差公式计算即可.
知识点 2
利用平方差公式进行简便计算
2.巧用公式计算:18×20-192.
解:原式=(19-1)(19+1)-192
=192-1-192= -1.
有的计算虽然不能从整体上用平方差公式,但可将其中一部分套入公式,适当拆项使整个运算更简捷些.
平方差公式的应用
知识点 3
3.计算:x(x+2)+(1+x)(1-x).
解:原式=x2+2x+1-x2=2x+1.
4.【例1】如图,利用图1和图2的阴影面积相等,写出一个正确的等式: .
(a+2)(a-2)=a2-4
5.【例2】计算:
(1)203×197;
(2)(x+2y)(x-2y)-y(3-4y).
解:原式=(200+3)(200-3)=2002-32
=40 000-9=39 991.
解:原式=x2-4y2-(3y-4y2)
=x2-4y2-3y+4y2=x2-3y.
6.【例3】先化简,再求值:
(2+a)(2-a)-,其中a=2.
解:原式=4-a2-a2+1=5- a2.
当a=2时,
原式=5- ×4=0.
7.(创新题)在边长为a的正方形中挖掉一个边长为b的小正方形
(a>b),把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是
( )
A.a2-b2=(a+b)(a-b)
B.(a+b)2 =a2+2ab+b2
C.(a-b)2=a2-2ab+b2
D.a2-ab=a(a-b)
A
8.用平方差公式计算:
(1)2 023×2 025-2 0242;
(2)(a+3b)(a-3b)(a2+9b2).
解:原式=(2 024-1)×(2 024+1)-2 0242
=2 0242-1-2 0242=1.
解:原式=(a2-9b2)(a2+9b2)=a4-81b4.
9.已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
解:原式=9x2-4+x2-2x=10x2-2x-4,
因为5x2-x-1=0,所以5x2-x=1.
所以原式=2(5x2-x)-4= -2.
★10. 0.40(代数推理)观察下列各式:(2+3)2-22=7×3;(4+3)2-42=11×3;(6+3)2-62=15×3,….不难发现规律:比任意一个偶数大3的数与此偶数的平方差能被3整除.
(1)(8+3)2-82的结果是3的 倍;
(2)设偶数为2n,试说明比2n大5的数与2n的平方差能被5整除;
解:(2)根据题意可知,设偶数为2n,则比2n大5的数为2n+5,
因为(2n+5)2-(2n)2=(2n+5-2n)(2n+5+2n)=5(4n+5),4n+5为整数,所以5(4n+5)能被5整除,
所以比2n大5的数与2n的平方差能被5整除.
19
(3)拓展:比任意一个正整数大5的数与此整数的平方差除以10的余数是 .
5
布置作业
请完成课后对应习题
感谢大家观看
同课章节目录
