2024-2025学年北师大版七年级数学下册1.3乘法公式课时4 乘法公式的运用 课件(共30张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册1.3乘法公式课时4 乘法公式的运用 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 254.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:23:35 | ||
图片预览











文档简介
(共30张PPT)
北师大版七年级数学下册课件
第一章 整式的乘除
1.3乘法公式
课时4 乘法公式的运用
1.进一步掌握完全平方公式;
2.灵活运用完全平方公式进行计算.(重点,难点)
学习目标
新课导入
思 考
(1)两个公式中的字母都能表示什么
(2)完全平方公式在计算化简中有些什么作用
(3)根据两数和或差的完全平方公式,能够计算
多个数的和或差的平方吗
(a+b) 2=a2+2ab+b2
(a-b) 2=a2-2ab+b2
1.完全平方公式:
新课讲解
知识点1 完全平方公式的运用
思考:怎样计算1022,992更简便呢?
(1) 1022;
解:原式= (100+2)2
=10000+400+4
=10404.
(2) 992.
解:原式= (100 –1)2
=10000 -200+1
=9801.
新课讲解
例1 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ;
原式=[x+(2y–3)][x-(2y-3)]
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
解: (1)
方法总结:用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.
新课讲解
(2) (a+b+c)2.
解:原式= [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2bc+2ac.
方法总结:要把其中两项看成一个整体,再按照完全平方公式进行计算.
新课讲解
例2 化简:(x-2y)(x2-4y2)(x+2y).
解:原式=(x-2y)(x+2y)(x2-4y2)
=(x2-4y2)2
=x4-8x2y2+16y4.
方法总结:先运用平方差公式,再运用完全平方公式.
新课讲解
完全平方公式的常见变形
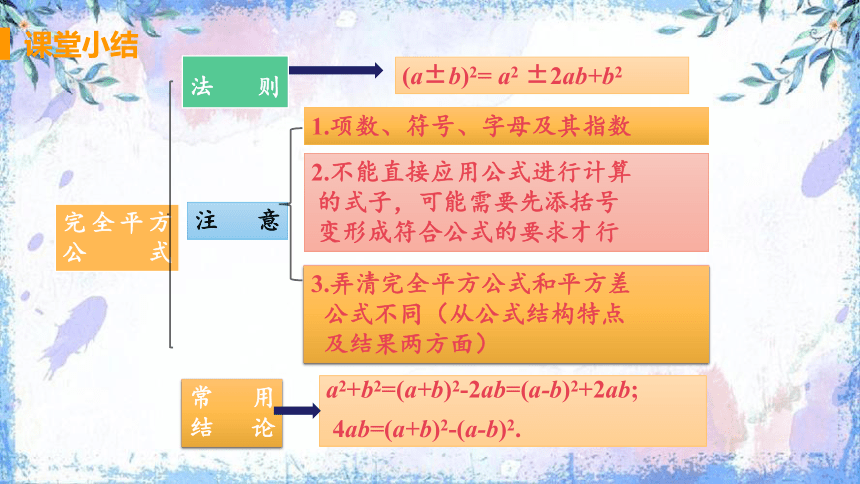
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算
的式子,可能需要先添括号
变形成符合公式的要求才行
常用
结论
3.弄清完全平方公式和平方差
公式不同(从公式结构特点
及结果两方面)
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
当堂小练
运用完全平方公式计算:
(1) 962 ; (2) 2032 .
解:原式=(100-4)2
=1002+42-2×100×4
=10000+16-800
=9216;
解:原式=(200+3)2
=2002+32++2×200×3
=40000+9+1200
=41209.
当堂小练
2.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
3.已知x2+y2=8,x+y=4,求x-y.
解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
解:∵x+y=4, ∴(x+y)2=16,即x2+y2+2xy=16①;
∵x2+y2=8②;
由①-②得2xy=8 ,
②- 得x2+y2-2xy=0.即(x-y)2=0,故x-y=0
解题时常用结论:
a2+b2=(a+b)2-2ab=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2.
去括号:
(1)a+(b+c)=a+b+c;
(2)a-(b+c)= .
知识点 1
去括号、添括号(复习)
a-b-c
1.添括号:
(1)a+b+c=a+( );
(2)a-b-c=a-( ).
b+c
b+c
运用添括号法则,把括号里各项分成两组,
先运用平方差公式:(a+b)(a-b)=a2-b2;
再运用完全平方公式:(a±b)2=a2±2ab+b2.
知识点 2
平方差公式的综合应用
2.计算:(x+y+1)(x+y-1).
解:原式=[(x+y)+1][(x+y)-1]
=(x+y)2-12=x2+2xy+y2-1.
运用添括号法则,先把括号里各项分成两大项,
再运用完全平方公式:(a±b)2=a2±2ab+b2.
知识点 3
完全平方公式的综合应用
3.(人教8上P111)计算:(a-b+1)2.
解:原式=[(a-b)+1]2=(a-b)2+2(a-b)+1
=a2-2ab+b2+2a-2b+1.
计算:(x+y)2-(x+y)(x-y).
知识点 4
整式乘法的综合运算(含两个公式)
解:原式=x2+2xy+y2-x2+y2=2y2+2xy.
4.计算:x(x+6)+(x-3)2.
解:原式=x2+6x+x2-6x+9=2x2+9.
5.【例1】利用完全平方公式计算:2012.
解:原式=(200+1)2=2002+2×200×1+1=40 401.
6.【例2】计算:
(1)(2x+1)2-4x2;
(2)(a+b-2)(a-b+2)
解:原式=4x2+4x+1-4x2=4x+1.
解:原式=[a+(b-2)][a-(b-2)]=a2-(b-2)2=a2-(b2-4b+4)
=a2-b2+4b-4.
7.【例3】(北师7下P25)一个底面是正方形的长方体,高为 6 cm,底面正方形边长为 5 cm,如果它的高不变,底面正方形边长增加了 a cm,那么它的体积增加了多少?
解:根据题意,体积增加了6(a+5)2-6×52
=6a2+60a+150-150=6a2+60a(cm3).
答:它的体积增加了(6a2+60a)cm3.
8.【例4】化简求值:(x-2y)2-4(x-y)(2x+y),其中x=1,y=-1.
解:原式=x2-4xy+4y2-4(2x2+xy-2xy-y2)
=x2-4xy+4y2-8x2+4xy+4y2
= -7x2+8y2.
当x=1,y= -1时,
原式= -7×12+8×(-1)2= -7+8=1.
9.利用完全平方公式计算:4992.
解:原式=(500-1)2=5002-2×500×1+1=249 001.
10.(人教8上P111改编)计算:
(1)a2b2-(ab-1)2;
(2)(a+2b)2-(a-2b)(a+2b).
解:原式=a2b2-(a2b2-2ab+1)=a2b2-a2b2+2ab-1=2ab-1.
解:原式=a2+4ab+4b2-(a2-4b2)
=a2+4ab+4b2-a2+4b2
=8b2+4ab.
11.一个正方形的边长增加2 cm,它的面积就增加了24 cm2,问这个正方形原来的边长是多少?
解:设这个正方形原来的边长为x cm,
根据题意得(x+2)2-x2=24,
即x2+4x+4-x2=24,解得x=5,
所以这个正方形原来的边长为 5 cm.
★12. 0.45已知4x=3y,求代数式(x-2y)2-(x-y)(x+y)-2y2的值.
解:原式=x2-4xy+4y2-x2+y2-2y2=3y2-4xy,
当4x=3y时,
原式=3y2-3y·y=3y2-3y2=0.
布置作业
请完成课后对应习题
感谢大家观看
北师大版七年级数学下册课件
第一章 整式的乘除
1.3乘法公式
课时4 乘法公式的运用
1.进一步掌握完全平方公式;
2.灵活运用完全平方公式进行计算.(重点,难点)
学习目标
新课导入
思 考
(1)两个公式中的字母都能表示什么
(2)完全平方公式在计算化简中有些什么作用
(3)根据两数和或差的完全平方公式,能够计算
多个数的和或差的平方吗
(a+b) 2=a2+2ab+b2
(a-b) 2=a2-2ab+b2
1.完全平方公式:
新课讲解
知识点1 完全平方公式的运用
思考:怎样计算1022,992更简便呢?
(1) 1022;
解:原式= (100+2)2
=10000+400+4
=10404.
(2) 992.
解:原式= (100 –1)2
=10000 -200+1
=9801.
新课讲解
例1 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ;
原式=[x+(2y–3)][x-(2y-3)]
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
解: (1)
方法总结:用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.
新课讲解
(2) (a+b+c)2.
解:原式= [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2bc+2ac.
方法总结:要把其中两项看成一个整体,再按照完全平方公式进行计算.
新课讲解
例2 化简:(x-2y)(x2-4y2)(x+2y).
解:原式=(x-2y)(x+2y)(x2-4y2)
=(x2-4y2)2
=x4-8x2y2+16y4.
方法总结:先运用平方差公式,再运用完全平方公式.
新课讲解
完全平方公式的常见变形
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算
的式子,可能需要先添括号
变形成符合公式的要求才行
常用
结论
3.弄清完全平方公式和平方差
公式不同(从公式结构特点
及结果两方面)
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
当堂小练
运用完全平方公式计算:
(1) 962 ; (2) 2032 .
解:原式=(100-4)2
=1002+42-2×100×4
=10000+16-800
=9216;
解:原式=(200+3)2
=2002+32++2×200×3
=40000+9+1200
=41209.
当堂小练
2.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
3.已知x2+y2=8,x+y=4,求x-y.
解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
解:∵x+y=4, ∴(x+y)2=16,即x2+y2+2xy=16①;
∵x2+y2=8②;
由①-②得2xy=8 ,
②- 得x2+y2-2xy=0.即(x-y)2=0,故x-y=0
解题时常用结论:
a2+b2=(a+b)2-2ab=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2.
去括号:
(1)a+(b+c)=a+b+c;
(2)a-(b+c)= .
知识点 1
去括号、添括号(复习)
a-b-c
1.添括号:
(1)a+b+c=a+( );
(2)a-b-c=a-( ).
b+c
b+c
运用添括号法则,把括号里各项分成两组,
先运用平方差公式:(a+b)(a-b)=a2-b2;
再运用完全平方公式:(a±b)2=a2±2ab+b2.
知识点 2
平方差公式的综合应用
2.计算:(x+y+1)(x+y-1).
解:原式=[(x+y)+1][(x+y)-1]
=(x+y)2-12=x2+2xy+y2-1.
运用添括号法则,先把括号里各项分成两大项,
再运用完全平方公式:(a±b)2=a2±2ab+b2.
知识点 3
完全平方公式的综合应用
3.(人教8上P111)计算:(a-b+1)2.
解:原式=[(a-b)+1]2=(a-b)2+2(a-b)+1
=a2-2ab+b2+2a-2b+1.
计算:(x+y)2-(x+y)(x-y).
知识点 4
整式乘法的综合运算(含两个公式)
解:原式=x2+2xy+y2-x2+y2=2y2+2xy.
4.计算:x(x+6)+(x-3)2.
解:原式=x2+6x+x2-6x+9=2x2+9.
5.【例1】利用完全平方公式计算:2012.
解:原式=(200+1)2=2002+2×200×1+1=40 401.
6.【例2】计算:
(1)(2x+1)2-4x2;
(2)(a+b-2)(a-b+2)
解:原式=4x2+4x+1-4x2=4x+1.
解:原式=[a+(b-2)][a-(b-2)]=a2-(b-2)2=a2-(b2-4b+4)
=a2-b2+4b-4.
7.【例3】(北师7下P25)一个底面是正方形的长方体,高为 6 cm,底面正方形边长为 5 cm,如果它的高不变,底面正方形边长增加了 a cm,那么它的体积增加了多少?
解:根据题意,体积增加了6(a+5)2-6×52
=6a2+60a+150-150=6a2+60a(cm3).
答:它的体积增加了(6a2+60a)cm3.
8.【例4】化简求值:(x-2y)2-4(x-y)(2x+y),其中x=1,y=-1.
解:原式=x2-4xy+4y2-4(2x2+xy-2xy-y2)
=x2-4xy+4y2-8x2+4xy+4y2
= -7x2+8y2.
当x=1,y= -1时,
原式= -7×12+8×(-1)2= -7+8=1.
9.利用完全平方公式计算:4992.
解:原式=(500-1)2=5002-2×500×1+1=249 001.
10.(人教8上P111改编)计算:
(1)a2b2-(ab-1)2;
(2)(a+2b)2-(a-2b)(a+2b).
解:原式=a2b2-(a2b2-2ab+1)=a2b2-a2b2+2ab-1=2ab-1.
解:原式=a2+4ab+4b2-(a2-4b2)
=a2+4ab+4b2-a2+4b2
=8b2+4ab.
11.一个正方形的边长增加2 cm,它的面积就增加了24 cm2,问这个正方形原来的边长是多少?
解:设这个正方形原来的边长为x cm,
根据题意得(x+2)2-x2=24,
即x2+4x+4-x2=24,解得x=5,
所以这个正方形原来的边长为 5 cm.
★12. 0.45已知4x=3y,求代数式(x-2y)2-(x-y)(x+y)-2y2的值.
解:原式=x2-4xy+4y2-x2+y2-2y2=3y2-4xy,
当4x=3y时,
原式=3y2-3y·y=3y2-3y2=0.
布置作业
请完成课后对应习题
感谢大家观看
同课章节目录
