7. 6 用锐角三角函数解决问题(第 1 课时) 同步练习(无答案) 2024-2025学年九年级下册数学苏科版
文档属性
| 名称 | 7. 6 用锐角三角函数解决问题(第 1 课时) 同步练习(无答案) 2024-2025学年九年级下册数学苏科版 |
|
|
| 格式 | docx | ||
| 文件大小 | 50.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-13 13:27:45 | ||
图片预览

文档简介
7. 6 用锐角三角函数解决问题(第 1 课时)
1. 在 △ABC中 , ∠C= 90°, ∠A= 45°,则 BC ∶AC ∶AB= 。
2. 在 △ABC中 , ∠C= 90°, ∠A= 30°,则 BC ∶AC ∶AB= 。
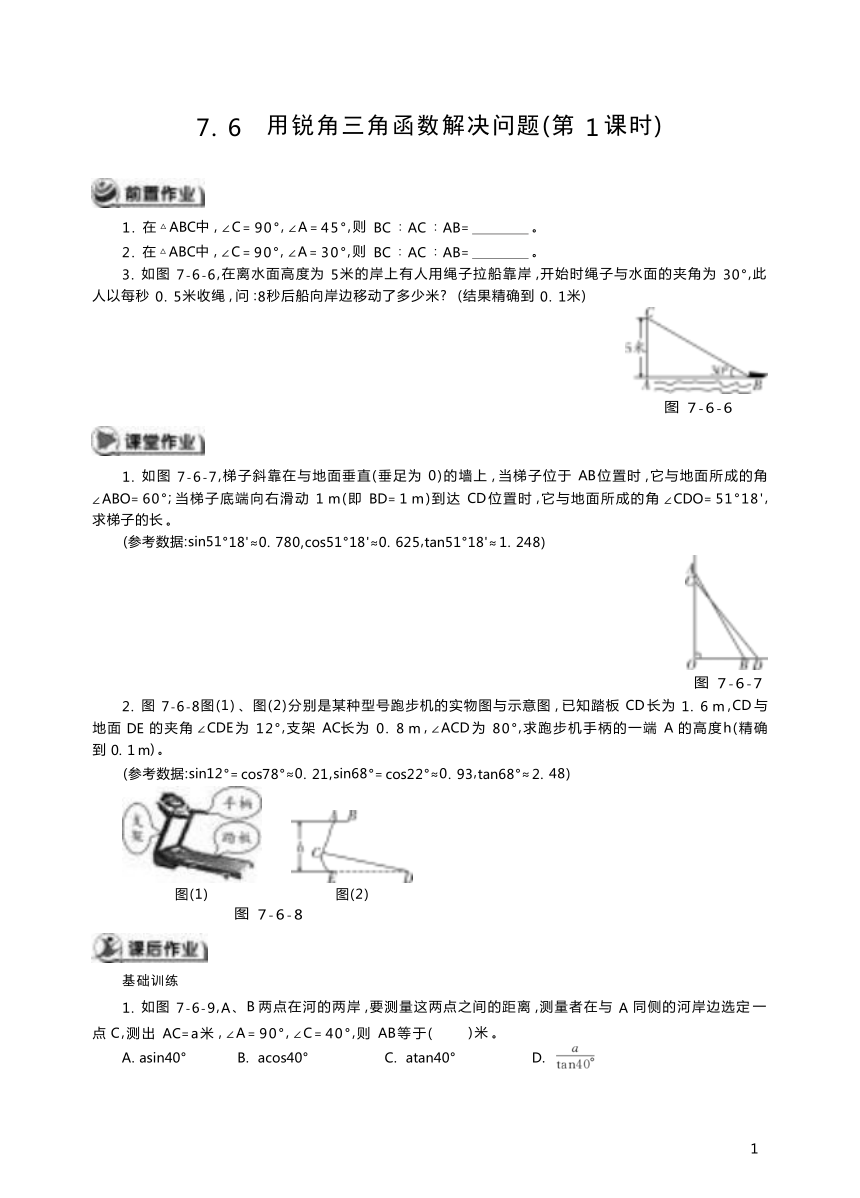
3. 如图 7-6-6,在离水面高度为 5米的岸上有人用绳子拉船靠岸 ,开始时绳子与水面的夹角为 30°,此 人以每秒 0. 5米收绳 , 问 :8秒后船向岸边移动了多少米 (结果精确到 0. 1米)
图 7-6-6
1. 如图 7-6-7,梯子斜靠在与地面垂直(垂足为 0)的墙上 , 当梯子位于 AB 位置时 ,它与地面所成的角 ∠ABO= 60°; 当梯子底端向右滑动 1 m(即 BD= 1 m)到达 CD 位置时 ,它与地面所成的角 ∠CDO= 51°18', 求梯子的长 。
(参考数据:sin51°18'≈0. 780,cos51°18'≈0. 625,tan51°18'≈ 1. 248)
图 7-6-7
2. 图 7-6-8图(1) 、图(2)分别是某种型号跑步机的实物图与示意图 , 已知踏板 CD 长为 1. 6 m ,CD 与 地面 DE 的夹角 ∠CDE 为 12°,支架 AC长为 0. 8 m , ∠ACD 为 80°,求跑步机手柄的一端 A 的高度h(精确 到 0. 1 m) 。
(参考数据:sin12°= cos78°≈0. 21,sin68°= cos22°≈0. 93,tan68°≈ 2. 48)
图(1) 图(2)
图 7-6-8
基础训练
1. 如图 7-6-9,A、B 两点在河的两岸 ,要测量这两点之间的距离 ,测量者在与 A 同侧的河岸边选定 一 点 C,测出 AC=a米 , ∠A= 90°, ∠C= 40°,则 AB 等于( )米 。
A. asin40° B. acos40° C. atan40° D.
1
图 7-6-9 图 7-6-10 图 7-6-11
2. 如图 7-6-10是一张简易活动餐桌 ,测得 OA=OB= 30 cm ,OC=OD= 50 cm ,B 点和 O 点时固定 的 。为了调节餐桌高矮 ,A 点有 3处固定点 ,分别使 ∠OAB 为 30°,45°,60°, 问这张餐桌调节到最低时桌面离 地面的高度是(不考虑桌面厚度)( ) 。
A. 40 2 B. 40 C. 40 3 D. 30
3. 在一次数学活动中 ,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪 , 去测量 学校内一座假山的高度 CD,如图 7-6-11, 已知小明距假山的水平距离 BD 为 12 m ,他的眼睛距地面的高 度为 1. 6 m ,李明的视线经过量角器零刻度线 OA 和假山的最高点 C,此时 ,铅垂线OE 经过量角器的 60°刻 度线 ,则假山的高度为( ) 。
A. ( 4 3 +1. 6) m B. ( 12 3 +1. 6) m C. ( 4 2 +1. 6) m D. 4 3 m
4. 如图 7-6-12, 已知AB⊥AE 于 A,EF⊥AE 于 E,要计算 A,B 两地的距离 , 甲 、乙 、丙 、丁四组同学 分别测量了部分线段的长度和角的度数 ,得到以下四组数据 :
甲 :AC、∠ACB;乙 :EF、DE、AD;丙:AD、DE 和 ∠DFE;
丁:CD、∠ACB、∠ADB、其中能求得 A,B 两地距离的有( ) 。
A. 1组 B. 2组 C. 3组 D. 4组
图 7-6-12 图 7-6-13 图 7-6-14
5. 如图 7-6-13,河流两岸 a、b互相平行 ,点 A、B 是河岸 a 上的两座建筑物 ,点 C、D 是河岸 b 上的两 点 ,A、B 的距离约为 200米 。某人在河岸b上的点 P 处测得 ∠APC= 75°, ∠BPD= 30°,则河流的宽度约为 米 。
6. 小聪有一块含有 30°角的直角三角板 ,他想只利用量角器来测量较短直角边的长度 ,于是他采用如图 7-6 -14的方法 ,小聪发现点 A处的三角板读数为 12 cm,点 B处的量角器的读数为 74°和 106°, 由此可知三角板的较
短直角边的长度为 cm。(参考数据:tan37°=0. 75) 拓展提高
7. 将一盒足量的牛奶按如图 7-6-15(1) 所示倒入一个水平放置的长方体容器中 , 当容器中的牛奶刚 好接触到点 P 时停止倒入图 7-6-15(2) 是它的平面示意图 ,请根据图中的信息 ,求出容器中牛奶的高度 (结果精确到 0. 1cm) 。 (参考数据 : 3 ≈ 1. 73, 2 ≈ 1. 41)
图(1) 图(2)
7-6-15
2
发散思维
8. 在一次科技活动中 ,小明进行了模拟雷达扫描实验 . 如图 7-6-24, 表盘是 △ABC,其中 AB=AC, ∠BAC= 120°,在点 A 处有一束红外光线 AP ,从 AB开始 ,绕点 A 逆时针匀速旋转 , 每秒钟旋转 15°, 到达 AC后立即以相同旋转速度返回 AB,到达后立即重复上述旋转过程 。 小明通过实验发现 ,光线从 AB 处旋
转开始计时 ,旋转 1秒 ,此时光线 AP 交 BC 边于点 M ,BM 的长为
(1)求 AB的长 ;
(2)从 AB 处旋转开始计时 ,若旋转 6秒 ,此时光线 AP与 BC 边的交点在什么位置 若旋转 201秒 ,交 点又在什么位置 请说明理由 。
图 7-6-16
3
1. 在 △ABC中 , ∠C= 90°, ∠A= 45°,则 BC ∶AC ∶AB= 。
2. 在 △ABC中 , ∠C= 90°, ∠A= 30°,则 BC ∶AC ∶AB= 。
3. 如图 7-6-6,在离水面高度为 5米的岸上有人用绳子拉船靠岸 ,开始时绳子与水面的夹角为 30°,此 人以每秒 0. 5米收绳 , 问 :8秒后船向岸边移动了多少米 (结果精确到 0. 1米)
图 7-6-6
1. 如图 7-6-7,梯子斜靠在与地面垂直(垂足为 0)的墙上 , 当梯子位于 AB 位置时 ,它与地面所成的角 ∠ABO= 60°; 当梯子底端向右滑动 1 m(即 BD= 1 m)到达 CD 位置时 ,它与地面所成的角 ∠CDO= 51°18', 求梯子的长 。
(参考数据:sin51°18'≈0. 780,cos51°18'≈0. 625,tan51°18'≈ 1. 248)
图 7-6-7
2. 图 7-6-8图(1) 、图(2)分别是某种型号跑步机的实物图与示意图 , 已知踏板 CD 长为 1. 6 m ,CD 与 地面 DE 的夹角 ∠CDE 为 12°,支架 AC长为 0. 8 m , ∠ACD 为 80°,求跑步机手柄的一端 A 的高度h(精确 到 0. 1 m) 。
(参考数据:sin12°= cos78°≈0. 21,sin68°= cos22°≈0. 93,tan68°≈ 2. 48)
图(1) 图(2)
图 7-6-8
基础训练
1. 如图 7-6-9,A、B 两点在河的两岸 ,要测量这两点之间的距离 ,测量者在与 A 同侧的河岸边选定 一 点 C,测出 AC=a米 , ∠A= 90°, ∠C= 40°,则 AB 等于( )米 。
A. asin40° B. acos40° C. atan40° D.
1
图 7-6-9 图 7-6-10 图 7-6-11
2. 如图 7-6-10是一张简易活动餐桌 ,测得 OA=OB= 30 cm ,OC=OD= 50 cm ,B 点和 O 点时固定 的 。为了调节餐桌高矮 ,A 点有 3处固定点 ,分别使 ∠OAB 为 30°,45°,60°, 问这张餐桌调节到最低时桌面离 地面的高度是(不考虑桌面厚度)( ) 。
A. 40 2 B. 40 C. 40 3 D. 30
3. 在一次数学活动中 ,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪 , 去测量 学校内一座假山的高度 CD,如图 7-6-11, 已知小明距假山的水平距离 BD 为 12 m ,他的眼睛距地面的高 度为 1. 6 m ,李明的视线经过量角器零刻度线 OA 和假山的最高点 C,此时 ,铅垂线OE 经过量角器的 60°刻 度线 ,则假山的高度为( ) 。
A. ( 4 3 +1. 6) m B. ( 12 3 +1. 6) m C. ( 4 2 +1. 6) m D. 4 3 m
4. 如图 7-6-12, 已知AB⊥AE 于 A,EF⊥AE 于 E,要计算 A,B 两地的距离 , 甲 、乙 、丙 、丁四组同学 分别测量了部分线段的长度和角的度数 ,得到以下四组数据 :
甲 :AC、∠ACB;乙 :EF、DE、AD;丙:AD、DE 和 ∠DFE;
丁:CD、∠ACB、∠ADB、其中能求得 A,B 两地距离的有( ) 。
A. 1组 B. 2组 C. 3组 D. 4组
图 7-6-12 图 7-6-13 图 7-6-14
5. 如图 7-6-13,河流两岸 a、b互相平行 ,点 A、B 是河岸 a 上的两座建筑物 ,点 C、D 是河岸 b 上的两 点 ,A、B 的距离约为 200米 。某人在河岸b上的点 P 处测得 ∠APC= 75°, ∠BPD= 30°,则河流的宽度约为 米 。
6. 小聪有一块含有 30°角的直角三角板 ,他想只利用量角器来测量较短直角边的长度 ,于是他采用如图 7-6 -14的方法 ,小聪发现点 A处的三角板读数为 12 cm,点 B处的量角器的读数为 74°和 106°, 由此可知三角板的较
短直角边的长度为 cm。(参考数据:tan37°=0. 75) 拓展提高
7. 将一盒足量的牛奶按如图 7-6-15(1) 所示倒入一个水平放置的长方体容器中 , 当容器中的牛奶刚 好接触到点 P 时停止倒入图 7-6-15(2) 是它的平面示意图 ,请根据图中的信息 ,求出容器中牛奶的高度 (结果精确到 0. 1cm) 。 (参考数据 : 3 ≈ 1. 73, 2 ≈ 1. 41)
图(1) 图(2)
7-6-15
2
发散思维
8. 在一次科技活动中 ,小明进行了模拟雷达扫描实验 . 如图 7-6-24, 表盘是 △ABC,其中 AB=AC, ∠BAC= 120°,在点 A 处有一束红外光线 AP ,从 AB开始 ,绕点 A 逆时针匀速旋转 , 每秒钟旋转 15°, 到达 AC后立即以相同旋转速度返回 AB,到达后立即重复上述旋转过程 。 小明通过实验发现 ,光线从 AB 处旋
转开始计时 ,旋转 1秒 ,此时光线 AP 交 BC 边于点 M ,BM 的长为
(1)求 AB的长 ;
(2)从 AB 处旋转开始计时 ,若旋转 6秒 ,此时光线 AP与 BC 边的交点在什么位置 若旋转 201秒 ,交 点又在什么位置 请说明理由 。
图 7-6-16
3
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
